异型矩阵序列的灰色绝对关联度模型及其应用

柯宏发， 祝冀鲁， 徐　勇

(1. 装备学院装备试验系, 北京 102206; 2. 工程设计研究总院信息工程室, 北京 100028)



异型矩阵序列的灰色绝对关联度模型及其应用

柯宏发1， 祝冀鲁1， 徐勇2

(1. 装备学院装备试验系, 北京 102206; 2. 工程设计研究总院信息工程室, 北京 100028)

摘要：针对同型矩阵及其序列有时无法全面描述多属性评估的问题，给出了异型矩阵序列的概念及其内涵，建立了异型矩阵序列的灰色绝对关联度模型，并通过超短波地面通信对抗系统作战效能评估实例验证了模型的合理性和有效性。最后就模型的系统化思维、模型的稳健性、理想矩阵序列的确定方法以及权重等问题进行了讨论，并指出了下一步的研究方向。

关键词：系统工程方法； 灰色关联分析； 异型矩阵序列； 灰色绝对关联度； 效能评估

灰色系统理论是一门研究少数据、贫信息不确定问题的学科，自1982年邓聚龙教授首次提出以来，由于其理论研究与应用价值，已成功应用于交通、农业、经济和军事等诸多领域[1-2]。笔者将其应用于武器装备试验领域，经过多年的研究与探索，已取得了一定的研究成果[3-6]，成功地解决了电子装备试验方案的优化选择、小样本试验数据的处理等难题。灰色关联分析是灰色系统理论的重要分支，其基本思想是根据序列曲线形状几何特征的相似程度来判断不同序列之间的相关程度，灰色关联度模型的建立与改进是灰色关联分析的重要研究方向，基于灰色关联度的灰靶决策方法、评估方法等更是取得了很多研究成果[3-8]，如笔者提出的电子装备作战效能的灰色关联评估模型[5]、灰色关联投影决策模型[6]等。但对于基于数据序列的灰色关联度模型，无论如何构建与优化关联度模型，其固有的缺陷都是无法避免的，如：初始化算子和分辨系数的变化会导致关联度甚至关联序的差异；以一维数据序列描述多属性决策与评估问题，忽略了属性信息的动态特征等。因此，张可[9]及熊和金等[10]考虑数据的多维度表现，提出了数据的矩阵、矩阵序列描述，并建立了矩阵及矩阵序列的一般灰色关联度模型和灰色绝对关联度模型；然而他们仅考虑了同型矩阵及其序列的情况，使其应用又受到了限制。特别是在武器装备试验活动中，很多多层次、多属性决策与评估问题无法用同型矩阵及其序列进行全面、系统的描述，因此选用异型矩阵或其序列进行描述具有更明显的物理意义。为此，笔者构建了异型矩阵序列的灰色绝对关联度模型，并通过通信对抗装备作战效能评估实例验证其合理性和有效性。

1装备试验数据的描述及其内涵

1.1矩阵描述及其内涵

假设矩阵J=(ai,j)M×N，K=(bi,j)M×N，2个矩阵的2个维度分别相等，则称矩阵J和K为同型矩阵，否则称为异型矩阵。

在武器装备试验活动中，利用矩阵对装备多性能属性试验数据进行整体描述，表示性能属性在2个维度方向上有行为表现，更符合实际工程应用背景，其物理意义也更明显。如：试验中对某种配试装备的选择是一个多属性决策过程，配试装备有多种属性指标，每个属性指标在不同的试验阶段有不同的行为表现。因此，一种类型的候选装备在属性维度和时间维度上都具有相应的值，则可表示为一个M×N矩阵，即

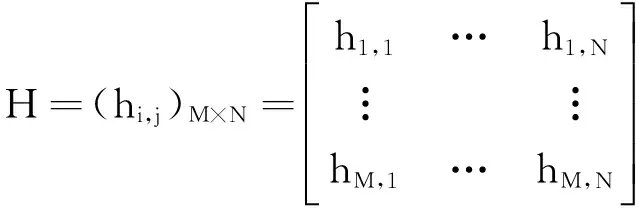
(1)

式中：hi,j为候选装备第i个属性指标在第j个时间点的行为表现值；M为候选装备的属性指标总数；N为时间点总数。

传统的方法是利用属性指标数据列描述该问题，只是基于简单化原则将时间维度退化为一个时间点而已，从而将动态多属性问题转化为静态多属性问题。但是对于多层次、多属性方案决策过程，如果基于矩阵进行描述，只能将方案行为维度退化为一种行为；否则，矩阵描述是无能为力的。其实，上述配试装备的选择过程就是基于配试装备某一种行为前提下进行的。

1.2矩阵序列描述及其内涵

对于数据列

A=(A1,A2,…,An)，

(2)

若Ak(k=1,2,…,n)为矩阵，则称A为矩阵序列。矩阵序列就是由一系列矩阵构成的“块状”数据列。

在矩阵序列A中，若A1,A2,…,An为同型矩阵，则称A为同型矩阵序列；若A1,A2,…,An中至少有2个矩阵相互为异型矩阵，则称A为异型矩阵序列。

由于武器装备试验活动中多层次、多属性方案决策问题的特征量通常在三维空间分布和变化，因此矩阵序列有效地解决了特征量的描述问题。例如：对于武器装备的作战效能评估问题，装备完成任务过程在作战能力、属性指标和时间3个维度上具有行为表现，因此，完成任务的程度在上述3个维度上具有属性值。假设利用矩阵序列A=(A1,A2,…,An)描述反映装备的作战效能，则Ak表示装备的第k种作战能力的行为矩阵，即

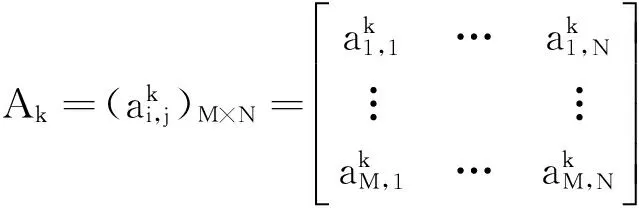
(3)

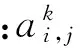
当N值足够大时，矩阵序列A反映了武器装备在整个作战过程中的效能行为表现，在进行作战效能评估时则可充分利用装备完成作战任务的行为表现信息，因而在一定程度上提高了评估结论的置信度和稳健度。目前，一般选取典型作战任务剖面进行装备作战效能评估，其实质就是退化了时间维度，忽视了装备行为信息的整体性和动态性，造成了评估信息的遗漏。另外，武器装备通常在各种作战能力属性指标维度上的行为表现差异很大，作战能力行为矩阵Ak相互之间表现出异型特征，因此，在大多数情况下，反映装备的作战效能矩阵序列A就是异型矩阵序列。

2同型矩阵序列的灰色绝对关联度

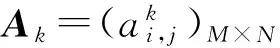
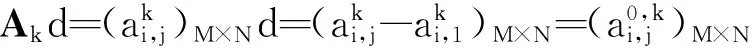
(4)

则称D为行为矩阵序列的始点零化算子，AD为A的始点零化像。记A的始点零化像为

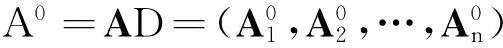
(5)

对于始点零化像A0，令

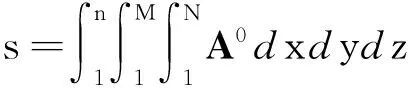
(6)

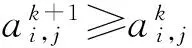
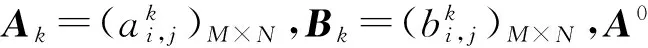
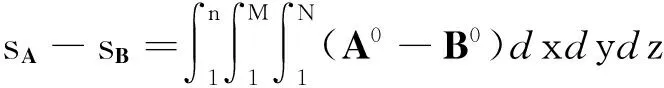
(7)

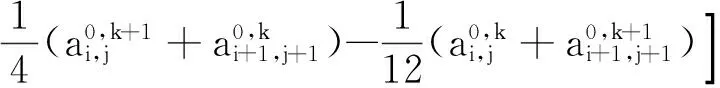
(8)

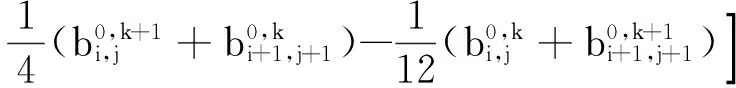
(9)

式中：sA、sB、分别为A0、B0在对应空间内的行为总量(即零化曲面与坐标平面围成的曲顶柱体体积)；sA-sB为A、B的行为表现差异(即2个零化曲面围成的曲顶柱体体积)。

则可以定义同型矩阵序列A和B的矩阵灰色绝对关联度为

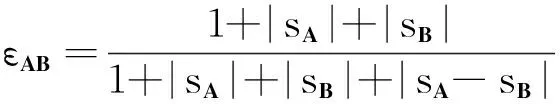
(10)

可以证明：同型矩阵灰色绝对关联度满足灰色关联四公理中的规范性、偶对称性和接近性等性质，但不满足整体性[9]。矩阵灰色绝对关联度更多地考虑了矩阵序列在空间的发展变化趋势，而不用考虑矩阵要素的相对重要性等系统因素的影响，在一定程度上克服了人为因素带来的不确定性影响。

3异型矩阵序列的灰色绝对关联度

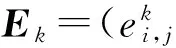
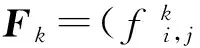
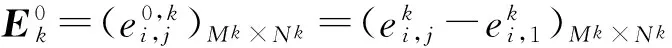
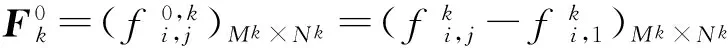
则有同型矩阵Ek和Fk的矩阵灰色绝对关联度为

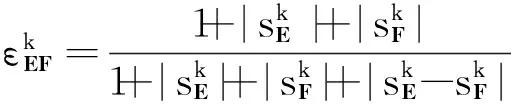
(11)

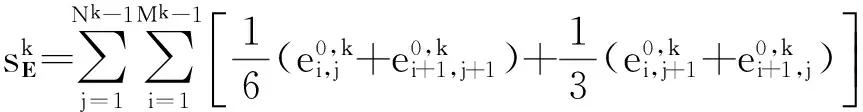
(12)

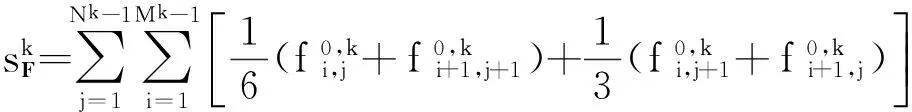
(13)

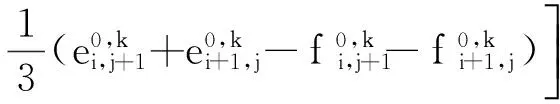
(14)

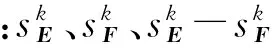
对于矩阵Ek和Fk，可求得其高度维度方向重心分别为ek和fk，则

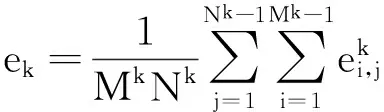
(15)

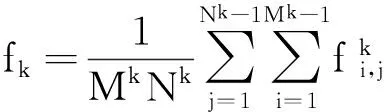
(16)

对于异型矩阵序列E和F，可假设其高度维度方向重心数据列为

XE=(e1,e2,…,en)，

(17)

XF=(f1,f2,…,fn)。

(18)

将XE、XF分别作为比较数据列、参考数据列，则可求得k点的灰色关联系数为

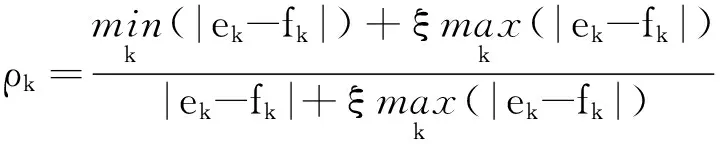
(19)

式中：ξ为分辨系数，通常取ξ=0.5。

则得到灰色关联系数数据列为ρ=(ρ1,ρ2,…,ρn)，对其进行归一化处理，得到权重数据列W=(w1,w2,…,wn)，其中

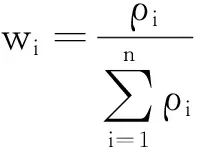
(20)

从而可得到异型矩阵序列E和F的矩阵灰色绝对关联度为

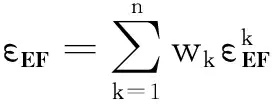
(21)

同样可以证明：异型矩阵灰色绝对关联度满足灰色关联四公理中的规范性、偶对称性和接近性等性质，但是也不满足整体性。

4通信对抗装备作战效能的矩阵灰关联分析

假设某型号超短波地面通信对抗系统由侦察控制站、测向站和干扰站组成，主要作战使命是在侦察控制站的指挥控制下，对敌无线电通信信号进行搜索、截获和分析，测定辐射源所在方位并进行定位，按指令对干扰目标进行人工控制或自动发射干扰。超短波通信对抗系统作战效能评估指标体系如图1所示，分别利用行为矩阵A1、A2、A3、A4、A5描述侦察能力、测向能力、干扰能力、指控能力和作战适用性，则可利用行为矩阵序列A=(A1,A2,A3,A4,A5)反映该系统的作战效能，于是该系统作战效能E可表示为

E=f(A)=f(A1,A2,A3,A4,A5)，

式中：f(·)为矩阵序列处理函数，明确其函数表达形式，即可得到该系统的作战效能值。

图1超短波通信对抗系统作战效能评估指标体系

该系统完成规定作战任务，假设侦察能力由侦察概率、侦察距离、侦察目标种类、作战使用适用性和作战环境适用性等属性确定，测向能力由测向距离、测向及定位精度、作战使用适用性和作战环境适用性等属性确定，干扰能力由干扰距离、目标压制效果、多目标干扰能力和作战使用适用性等属性确定，指控能力由通信传输正确率、情报处理能力、情报收集与分发能力、指挥与控制能力和作战使用适用性等属性确定，作战适用性由作战使用适用性、作战环境适用性和作战保障适用性等属性确定，行为矩阵Ai(i=1,2,…,5)数据已经过定量化和无量纲化等处理，则其完成任务全过程的行为矩阵序列表示为

很显然，A为异型矩阵序列，处理函数f(·)选用异型矩阵序列灰色绝对关联度模型。根据该系统完成历次作战任务的程度，确定其理想行为矩阵序列为

通过函数f(·)计算异型矩阵序列A和A0的灰色绝对关联度εAA0，2个矩阵的可视化表示分别如图2、3所示，可见：εAA0从整体上系统地衡量了2个曲面之间的接近性和相似性，物理意义很明显。

又由式(15)、(16)得到异型矩阵序列A和A0的高度维度方向重心数据列为

XA=(0.782 5,0.720 6,0.723 8,0.741 0,0.805 0)，

XA0=(0.903 5,0.836 9,0.840 0,0.861 0,0.915 0)。

图2系统完成任务的行为矩阵曲面

图3系统完成任务的理想行为矩阵曲面

由式(19)得到XA相对于XA0的灰色关联系数，进行归一化处理后，得到权重数据列W=(0.195 2,0.200 4,0.200 5,0.196 2,0.207 8)，从而由式(21)得到该系统完成该次任务的作战效能为

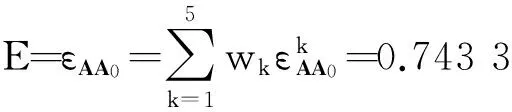
5讨论

5.1模型的系统化思维

武器装备作战效能评估问题关键体现在评估模型的选择和输入数据的描述2个方面。灰色关联分析以整体关联的系统化思想来寻求事物间的关联性，本文以装备完成规定任务所需的理想行为表现作为参考基准，通过衡量装备完成实际任务的行为表现与参考基准的接近性和相似性来达到评估作战效能的目标，而装备作战效能的本质定义就是装备完成规定任务之程度，可见该评估模型的物理意义很明显。针对输入数据，该模型利用矩阵序列描述装备在完成规定任务整个过程中的行为表现，不像传统装备作战效能评估那样选择典型的任务剖面数据，而是选择整个任务过程中连续的一系列任务剖面数据，也就不存在从典型到一般的推断假设。基于作战全过程的数据进行作战效能评估，提高了评估结果的置信度。因此，从整体性、系统性的角度来看，矩阵序列能刻画装备完成规定任务过程的动态性，评估结果不仅能直观地表现装备完成规定作战任务的程度，而且可以基于评估结论的关联序对装备的作战效能进行优势比较。

5.2模型的稳健性

针对矩阵序列中的侦察能力矩阵，假设其第3行属性指标值变大，考察矩阵序列灰色绝对关联度变化情况及其关联序。假设

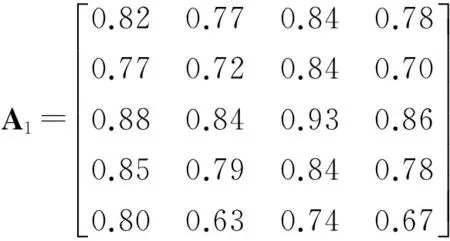
XA=(0.792 5,0.720 6,0.723 8,0.741 0,0.805 0)，

从而求得权重数据列

W=(0.204 2,0.198 1，0.198 2,0.194 0,0.205 4)，

则该系统的作战效能为

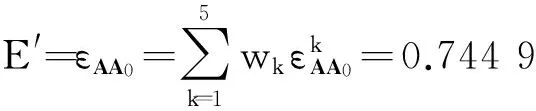
可见：侦察能力矩阵的变化也引起了作战效能的相应变化，且由于E′>E，侦察能力矩阵的变化并没有引起关联序的改变，可见该模型有效可行，稳健性较好。

5.3参考矩阵序列的确定方法

不管是计算矩阵序列的一般灰色关联度，还是计算其灰色绝对关联度，参考矩阵序列的确定都是模型应用的技术难点。对于武器装备的作战效能评估，参考矩阵序列就是指装备完成规定任务所需的理想行为表现序列。

确定武器装备作战效能评估的参考矩阵序列通常采取2种方法：1)根据武器装备完成规定作战任务的作战想定进行构建，基于想定的作战任务和作战进程，采用树状分析技术分解武器装备必须具备的作战能力和属性指标值；2)根据武器装备完成类似规定作战任务的历史数据进行构建，基于武器装备属性指标历史数据及其指标取值极型类型取得属性指标的最优值，其中极大值极型指标取最大值，极小值极型指标取最小值，居中型极型指标取适中值。

5.4权重的确定

图1所示的超短波通信对抗系统作战效能评估指标体系符合工程客观实际，每种能力所包含的能力要素存在一定的交叉性和相关性，这些能力要素对这种能力的贡献重要程度不同，而且交叉能力要素对不同的上层作战能力的影响重要程度也不同(如图1中指挥与控制能力同时对侦察能力和测向能力有影响，其影响重要程度不相同)，这些要素权重的确定问题一直是加权求和等聚合方法中的技术难点，总会受到人为不确定性因素的干扰。而矩阵序列的灰色绝对关联度模型直接根据评估数据进行灰色聚合，不需要确定能力要素之间、作战能力之间的权重，克服了人为主观因素对评估结果的影响。当然，如果采用矩阵序列的一般灰色关联度进行作战效能评估，求取能力要素之间、作战能力之间的权重还是必须解决的前提问题。

6结论

笔者提出了武器装备作战效能评估数据的异型矩阵序列灰色绝对关联度模型，并对模型的系统化思维、稳健性和理想矩阵序列的确定方法等问题进行了讨论。关于异型矩阵序列灰色绝对关联度模型在武器装备作战效能评估领域的应用问题，下一步的工作主要集中在2个方面：

1)矩阵序列的构建方法研究，矩阵序列的合理性对作战效能的评估结果具有重要的影响，其实质也可以归结为评估指标体系的建立问题，由于异型矩阵序列的灰色绝对关联度模型不考虑作战能力、能力要素的重要程度，作为评估模型的输入，矩阵序列的构建尤其重要；

2)基于矩阵序列的关键要素主次关系分析方法研究，灰色绝对关联度模型不能实现关键要素的主次关系分析，灵敏度分析只能说明系统作战效能易受到该能力要素的影响，但是不能说明能力要素的重要程度，因此需另行建模来分析能力要素的相对重要程度。

参考文献：

[1]LiuS,LinY.GreyInformation:TheoryandPracticalApplications[M].London:Springer, 2006.

[2]刘思峰，谢乃明，ForrestJ．基于相似性和接近性视角的新型灰色关联分析模型[J]．系统工程理论与实践，2010，30(5)：881-887.

[3]柯宏发，陈永光，刘波．电子装备试验方案的灰色优选模型及算法[J]．电子学报，2005，33(6)：995-998.

[4]KeHF,ChenYG,LiuY.DataProcessingofSmallSamplesBasedonGreyDistanceInformationApproach[J].JournalofSystemsEngineeringandElectronics, 2007，18(2)：281-289.

[5]KeHF,ChenYG,WangGY.GreyRelationalEvaluationforCombatEffectivenessofElectronicEquipmentBasedonIdealReferenceSequence[C]∥Proceedingsof5thIEEEInternationalConferenceonCognitiveInformatics.Beijing,China:IEEE,2006, 2：918-922.

[6]KeHF,LiuSF.SimilaritytoIdealGreyRelationalProjectionMethodforMultipleCriteriaDecision-Making[C]∥Proceedingsof2009IEEEInternationalConferenceonGreySystemsandIntelligentServices.Nanjing,China:IEEE, 2009, 2: 1008-1012.

[7]WangP,MengP,SongBW.ResponseSurfaceMethodUsingGreyRelationalAnalysisforDecisionMakinginWeaponSystemSelection[J].JournalofSystemsEngineeringandElectronics, 2014, 25(2):265-272.

[8]WangJK,NingHS,ChenWS,etal.AirportBird-strikeRiskAssessmentModelwithGreyClusteringEvaluationMethod[J].ChineseJournalofElectronics, 2012, 21(3):409-413.

[9]张可．矩阵型灰色关联分析建模技术研究[D]．南京：南京航空航天大学，2010.

[10]熊和金，陈绵云，瞿坦．灰色关联度公式的几种拓广[J]．系统工程与电子技术，2000，22(1)：8-10.

(责任编辑: 尚彩娟)

Grey Absolute Relational Degree Model of Heterotypic Matrix Sequence and its Application

KEHong-fa1,ZHUJi-lu1,XUYong2

(1.DepartmentofEquipmentTest,EquipmentAcademy,Beijing102206,China；2.DepartmentofInformationEngineering,CenterforEngineeringDesignandResearch,Beijing100028,China)

Keywords:systemengineeringmethod;greyrelationalanalysis;heterotypicmatrixsequence;greyabsoluterelationaldegree;effectivenessevaluation

Abstract：It’sdifficultforhomotypicmatrixandhomotypicmatrixsequencetofullydescribethemulti-attributeevaluationproblemsoccasionally,sotheconceptandconnotationofheterotypicmatrixsequenceispresented,andagreyabsoluterelationaldegreemodelofheterotypicmatrixsequenceissetup.Then,therationalityandvalidityofthemodelisverifiedbyevaluatingtheoperationaleffectivenessofgroundultrashortwavecommunicationcountermeasuresystemexample.Finally,somekeypointssuchassystematicthinking,robustnessofthemodel,determinationmethodofidealmatrixsequenceandweightsarediscussed,andthefutureresearchdirectionispointedout.

文章编号：1672-1497(2016)03-0094-06

收稿日期：2016-03-07

基金项目：军队科研计划项目

作者简介：柯宏发(1969-)，男，教授，博士。

中图分类号：E917；N941.5

文献标志码：A

DOI：10.3969/j.issn.1672-1497.2016.03.020