用简单的数形结合思想和微分证明微积分基本公式
2016-07-06 07:18:37夏沛庭
数学学习与研究 2016年11期
夏沛庭

【摘要】微积分基本公式又称牛顿-莱布尼茨公式,是高等数学中极为重要的公式之一,却少有证明过程,使很多初学者缺少对微积分基本公式的直观理解,该文章中作者不用常见的中值定理方式证明,而是用微分的定义以及较为简单的数形结合思想证明微积分基本公式,让人对微积分基本公式产生更加形象具体的理解.
【关键词】微积分基本公式;牛顿-莱布尼茨基本公式;高等数学;函数;微分;微积分
一、微积分基本公式
在高等数学的学习中,微积分基本公式是必不可少的重要公式之一,却因为其证明方法少且复杂使得很多人心中缺少对微积分基本公式的直观认识.
定理:如果函數F(x)是连续函数f(x)在区间[a,b]上的一个原函数,则
∫baf(x)dx=F(b)-F(a).
依靠这个公式,我们可以把求导函数定积分的问题转化成求原函数增量的问题,大大减少了使用定义计算导函数定积分的计算量,给微积分提供了一个有效而简便的算法.
二、微积分基本公式的证明
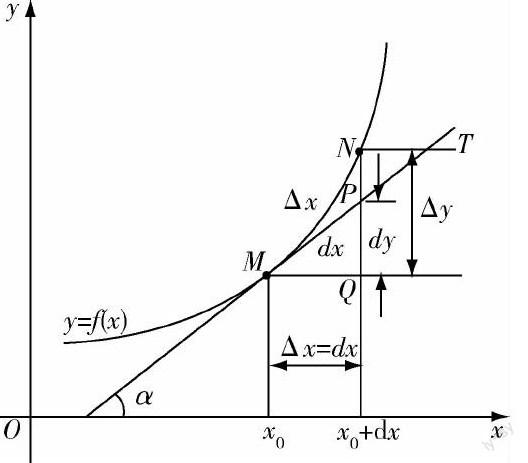
1.用微分和数形结合思想理解微积分基本公式
【参考文献】
[1]经济数学.微积分[M].北京:科学出版社,2011.
[2]数学分析新讲[M].北京:北京大学出版社,2011.
[3]微积分学教程.菲赫金哥尔茨[M].北京:人民教育出版社,2002.
猜你喜欢
数学物理学报(2021年2期)2021-06-09 08:54:26
中学生数理化(高中版.高考数学)(2020年9期)2020-10-28 08:44:04
中学生数理化(高中版.高考数学)(2020年9期)2020-10-28 08:44:04
中学生数理化(高中版.高考数学)(2020年9期)2020-10-28 08:43:56
数学物理学报(2019年5期)2019-11-29 07:46:34
小学生学习指导(中年级)(2019年10期)2019-10-08 09:11:38
小学生学习指导(中年级)(2017年4期)2017-03-20 15:46:51
广东技术师范大学学报(2016年5期)2016-08-22 09:07:22
作文与考试·小学高年级版(2016年7期)2016-05-14 05:39:03
中学数学杂志(高中版)(2016年1期)2016-02-23 23:08:03

