改进的CO2-原油体系范德华型组分混合规则
杨思玉,廉黎明,李实,杨永智,陈兴隆(1.提高石油采收率国家重点实验室;2.国家能源二氧化碳驱油与埋存技术研发(实验)中心;3.中国石油勘探开发研究院石油采收率研究所)
改进的CO2-原油体系范德华型组分混合规则
杨思玉1, 2, 3,廉黎明1, 2, 3,李实1, 2, 3,杨永智1, 2, 3,陈兴隆1, 2, 3
(1.提高石油采收率国家重点实验室;2.国家能源二氧化碳驱油与埋存技术研发(实验)中心;3.中国石油勘探开发研究院石油采收率研究所)
摘要:基于混合物状态方程分析、分子间相互作用关系理论,考虑温度、压力和非烃类组分相互作用等影响因素,改进了广泛应用的范德华型方程的混合规则,并推导出了对比状态的计算公式,形成了适用于高温高压条件下CO2-原油体系的新混合规则。通过还原为第二维里系数依赖关系的方法,证明了改进混合规则的理论严格性。以油田现场油样实测气相和液相组分数据为基础,在油藏温度和压力条件下,对混合规则改进前后计算油气组分等参数的精度进行对比。结果表明,新混合规则不仅计算简便,而且精度显著提高,组分计算加权平均误差由15%降至4%,密度计算加权平均误差由10%降至3%以下,满足工程应用要求。图2表2参23
关键词:CO2-原油体系;状态方程;组分混合规则;对比状态;闪蒸计算;逸度方程
0 引言
气液体系相态研究是分析和认识体系的重要手段[1-3],通过温压条件及组分变化表征。这一过程需要研究各组分和相间的相互作用,需要引入或应用混合规则来处理计算方法及实测或抽象物理量,使之可应用于混合物质。
混合规则从范德华状态方程出现开始,便陆续有大量研究,按应用形式和理论基础分以下几类:维里型、范德华(vdW)型[4-5]、交互作用参数与组成有关型[6]及基于过量自由能模型的局部组成型[7-9]。
这些混合规则虽各具优势,却也存在不足:维里型参数过多且不易通过实验回归,常用二阶舍项(也称二次截断型)维里方程,导致其只适用于描述低密度流体;vdW型只针对非理想性不强的体系,对高温高压条件考虑不足;交互参数与组成相关型只修正引力参数,并且由于相互作用参数是与组成相关的经验公式而无法恢复到第二维里系数形式,理论上不够严谨且具有“Michelsen-Kistenmacher综合症”[10];基于过量自由能模型的局部组成型绝大部分不能恢复为第二维里系数形式,理论上不够严谨,且模型计算复杂。
CO2-原油体系是典型的非理想体系[11],且处于高温高压状态,对混合规则有较高要求。本文在符合理论严谨的条件下,对原有vdW型混合规则进行改进,使其既符合第二维里系数的相互依赖关系,又计算简便,同时符合工业精度要求,并较好地适用于CO2-原油体系相态计算。
1 混合物状态方程
通常用Soave-Redlich-Kwong(SRK)[12-13]和Peng-Robinson(PR)[14]状态方程描述CO2-原油体系体积和密度之间的相互作用关系,SRK和PR方程属于立方型状态方程,函数形式简洁,在保持合理精度下易于计算,应用最为广泛,常用于数值计算中,统一函数形式如下:

(1)式是在纯净物质研究的基础上通过理论假设和实验回归得到的。对于多组分实际体系,由于各组分间的相互作用不同,不能直接应用,需引入组分混合规则。
2 vdW型混合规则及其改进
现有的几类混合规则各具特点[4-9],但用于高温高压的CO2-原油体系时,并不能同时满足计算简便、理论严格和符合工业使用精度等要求,需要在使用过程中完善。笔者针对形式简洁、计算简便的vdW型混合规则进行研究,并对其改进,使其适用于高温高压下非烃类-烃类混合体系的相态参数计算。
2.1 现有vdW型混合规则
混合规则中最早提出的是vdW单流体混合规则,其后,凡是符合vdW单流体混合规则形式的模型,都被称为vdW型混合规则,并具有下列形式:
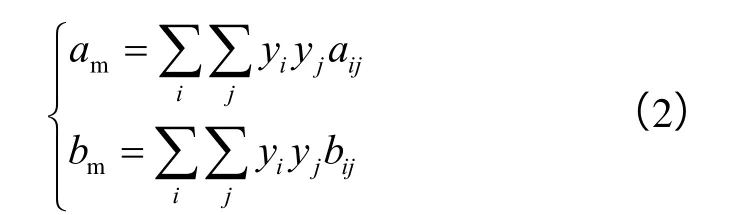
现在普遍使用的二元混合规则是Reid[15]修正Redlich-Kwong(RK)混合规则后提出的:
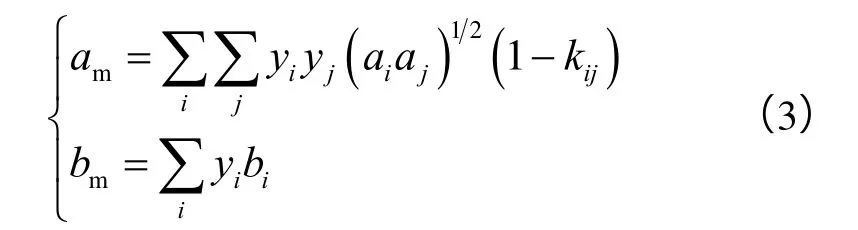
维里型混合规则基于严格统计力学[16],从理论上可以严格推导得出第q维维里系数是摩尔分数的q次函数,其形式如下:

由于维里型混合规则理论严格,因此常用作验证其他二元混合规则正确与否。
2.2 改进的vdW型混合规则
为了适用于高温高压下CO2-原油体系,对vdW型混合规则进行改进。
2.2.1 状态方程混合规则的改进
分析CO2-原油的一般体系可知,各组分间极性和对称性存在差异,设影响参数为lij,作用于斥力参数项;设压力产生的影响参数为dij,作用于斥力参数项(压力参数项);设温度产生的影响参数为eij,作用于引力函数项(温度函数项)。则新的混合规则为:
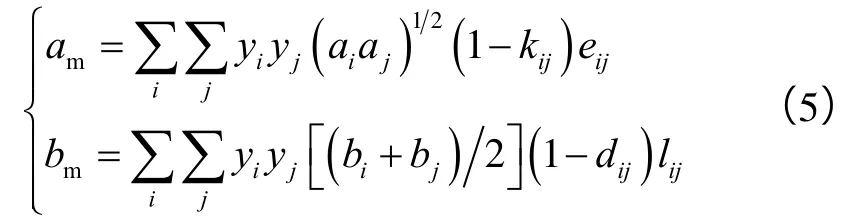
由前述可知,可用变换为第二维里参数形式的方法来验证新混合规则的理论严格性。对于立方型状态方程,第二维里系数可以表征为Bm=bm-am/RT,将(5)式带入得到:

可以看出,(6)式相当于(4)式中q=2的形式,符合第二维里系数对组成的二次依赖关系,因此改进混合规则符合理论严谨性。
2.2.2 对比状态及其他物理量的混合规则改进
对处于高温、高压状态的混合物体系,考虑到体系中各组分性质的差异,引入对比状态。将不同组分参数折算到同一参考系下考量,从而减少组分性质差异的影响。由于物质在临界状态时性质相似[17],因而常将各个组分的参量分别折算到本组分临界状态,然后进行计算。
将状态方程转化为对比条件状态方程,有:
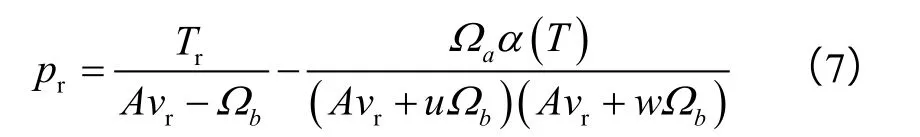
用对比状态方程进行混合物的描述时,还要对压力、温度和压缩因子等量进行混合计算。为了使SRK 和PR方程的参数混合规则能够应用对比状态原理,将应用于Redlich-Kwong方程的临界参数法应用在SRK 和PR方程上。
当用于混合物时,原RK方程总摩尔分数通式化为如下形式:

参照RK方程的临界参数法总摩尔分数通式,将PR和SRK方程改写为总摩尔分数通式形式:

其中,依新导出的混合规则:
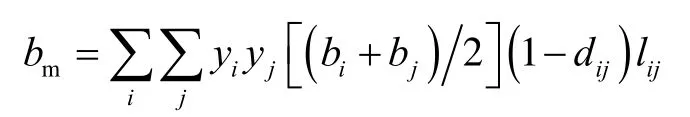
改进的添加项g(vm)为vm的函数,SPK方程中,g(vm)=0,PR方程中,g(vm)=bm-bm/vm。对于改进的Fm,在SRK方程中:

在PR方程中,Fm同(10)式,一般条件下

拟临界温度采用通用的定义:

拟临界压力采用通用的定义:

通过(5)式及(9)—(12)式,可将原本用于纯物质的状态方程应用于描述混合物的相态变化。
3 混合规则的应用方法
通常利用模拟闪蒸的方法应用混合规则,对体系组分的各项参数进行计算。
3.1 闪蒸方程
闪蒸计算时,闪蒸方程是由关联方程和限制条件组成的,严格推导可得到Rachford-Rice方程[18-19]:

3.2 混合物的逸度及逸度因子
根据热力学相平衡原理,当体系处于热力学平衡时,油气体系的每一组分在各相中的偏摩尔吉布斯自由能相等,即化学势相等[20],可转化为辅助函数逸度表示,也即油气体系的每一组分在各相中的逸度相等[21],对于油气两相,平衡条件如下:

逸度的计算公式可由逸度系数通过与状态方程的联系导出:

将导出的混合物状态方程带入,可得:

将逸度平衡条件(14)式与气液平衡常数关联,得到:
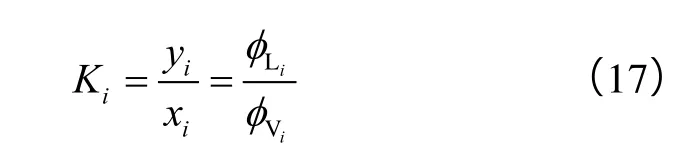
将上式取对数并写成残差形式,得:

将所推导的(9)式及新混合规则(5)式带入(18)式,并对Rachford-Rice方程进行迭代求解。每次迭代过程中,通过逸度平衡计算求取新的气液平衡常数,带入下一步迭代过程中。
将(5)式、(7)式、(9)式、(13)式、(16)式代入(18)式,通过Newton-Raphson迭代[22]或者超松弛迭代[23],可对体系的相态参数进行计算。
4 实例计算
选取4个未脱气的实际油样进行分析,温度、压力条件分别选取常温常压条件(温度20 ℃,压力0.1 MPa)和高温高压条件(地层温度,压力25.0 MPa),分别用未改进混合规则的状态方程和改进混合规则的状态方程进行计算(见图1、图2)。为减少迭代步骤,将测得的各组分合并为CO2、C1+N2、C2—7、C8—10、C11—22和C23+6个拟组分,分别用原混合规则和改进混合规则计算4个实际油样各组分的气相摩尔分数和液相摩尔分数数据(实验数据均来自中国石油勘探开发研究院),并将最终结果与实验数据对比(见表1)。最后得到各个组分在气相和液相中的摩尔组成,便可以进一步计算原油密度(见表2)。

图1 4个油样组分组成在常温常压下的原规则、改进混合规则计算值与实验数据比较
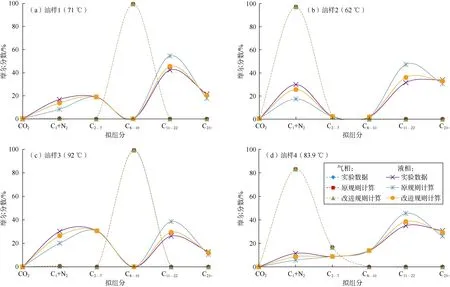
图2 4个实际油样组分组成在地层温度、25.0 MPa下的原规则、改进混合规则计算值与实验数据比较
由图1、图2和表1、表2可见:①原混合规则在计算这4个实际油样时误差较大,计算组分时加权平均误差超过15%,计算密度时加权平均误差超过10%;而改进的混合规则计算组分时的加权平均误差约为4%,计算密度时的加权平均误差不到3%,比较接近实际数据。改进的混合规则在计算高压条件和液相条件时比原有的混合规则更加具有优势。②此类混合规则无论是改进的还是原始的,计算气相组分的精度都要高于计算液相组分的精度,这种现象主要是由于所使用状态方程形式为两参数立方型状态方程导致,此类方程在计算液相时的精度要小于计算气相时的精度。③在计算C1+N2和C11—22组分时,计算精度有所下降,这是由于体系的非理想性增强造成的,N2分子结构比CO2更远离烃类分子结构,而C11—22组分之间存在C16石蜡点的性质偏差,导致非理想性增强。

表1 不同温压条件下4个实际油样组分不同混合规则计算误差

表2 不同温度压力下4个实际油样密度的实验数据和不同混合规则计算数据对比及误差分析
5 结论
本文提出的改进型混合规则计算精度有所提高,组分计算平均误差由15%降到4%,密度计算平均误差由10%降到3%以下,有助于提高基于体系组分和密度的相态准确性;模型遵循第二维里系数中各个参数的相互依赖关系,理论严谨;模型仅比vdW模型多了两个参数,保持了形式简洁和计算简便;由于多考虑了分子间的极性差异和温压差异的影响,模型对高温高压以及非理想条件的适应性增强;模型重新推导了对比状态表达式,有助于减小计算过程中由于假设形成的累计误差;模型对C1+N2组分模拟不够精确,是由于N2分子与烃类和CO2分子结构差异较大造成的,需要进行进一步研究。
符号注释:
A——绝对体积中的常数,可由状态方程求一阶和二阶导数并联立求解得到;a——状态方程引力项参数,(m3/mol)2·Pa;a(T)——温度函数,用于修正分子间引力,a(T)=α(T)ΩaR2Tc2/pc,(m3/mol)2·Pa;aij——组分i与j混合后状态方程引力项参数,aij=(aiaj)1/2(1-kij)eij,(m3/mol)2·Pa;b——状态方程斥力项参数,m3/mol;bij——组分i与j混合后状态方程斥力项参数,bij=[(bi+bj)/2](1-dij)lij,m3/mol;B——第二维里参数,m3/mol;dij——压力作用因子;eij——温度作用因子;f——逸度,Pa;F——偏心因子的函数;h1,h2,…,hq——体系中的h1,h2,…,hq组分;kij——二元交互作用因子,可以通过二元气-液平衡实验数据回归得到;K——气液平衡常数,Ki=yi/xi;lij——极性作用因子;NL, NV——液相和气相的相对体积,NV+NL=1;n——组分物质的量,mol;p——体系压力,MPa;R——普适气体常数,J/(mol·K);RES——残差;s1,s2——常数,SRK方程中s1=1、 s2=0,PR方程中T——体系温度,K; u,w——常数,对于SRK方程,u=0、w=1,对于PR方程,v——体系摩尔体积,m3/mol;V——体系体积,m3;Wq——第q维维里系数;——纯组分的维里系数;x——液相中某组分的摩尔分数,%;y——气相中某组分的摩尔分数,%;z——组分的摩尔分数,%;Z——压缩因子;α(T)——与温度相关的无因次因子,临界温度时其值为1,SRK方程中,α(T)=[1+(0.48+1.574ω-0.171 5ω2)(1-Tr1/2)]2,PR方程中,α(T)=[1+(0.374 64+1.542 26ω-0.269 92ω2)× (1-Tr1/2)]2,对于偏心因子较大的组分,α(T)=[1+(0.379 642+ 1.485 03ω-0.164 423ω2-0.016 666ω3)(1-Tr1/2)]2;φ——逸度因子(逸度系数);Ωa,Ωb——状态方程引力项和斥力项中的无因次常数,在SRK方程中,Ωa=0.427 480、Ωb=0.086 640,在PR方程中,Ωa=0.457 235、Ωb=0.077 796;ω——偏心因子。下标:c——临界状态;L——液相;m——混合物;r——对比状态;V——分压气相。
参考文献:
[1] 沈平平, 廖新维.二氧化碳地质埋存与提高石油采收率技术[M].北京: 石油工业出版社, 2009.SHEN Pingping, LIAO Xinwei.The technology of carbon dioxide stored in geological media and enhanced oil recovery[M].Beijing: Petroleum Industry Press, 2009.
[2] 秦积舜, 韩海水, 刘晓蕾.美国CO2驱油技术应用及启示[J].石油勘探与开发, 2015, 42(2): 209-216.QIN Jishun, HAN Haishui, LIU Xiaolei.Application and enlightenment of carbon dioxide flooding in the United States of America[J].Petroleum Exploration and Development, 2015, 42(2): 209-216.
[3] 廉黎明, 秦积舜, 杨思玉, 等.用于CO2-原油体系的改进型黏度预测模型[J].石油勘探与开发, 2014, 41(5): 591-596.LIAN Liming, QIN Jishun, YANG Siyu, et al.An improved viscosity model for CO2-crude system[J].Petroleum Exploration and Development, 2014, 41(5): 591-596.
[4] 童景山, 李敬.流体热物理性质的计算[M].北京: 清华大学出版社, 1982: 50-52.TONG Jingshan, LI Jing.Calculation of fluid thermophysical properties[M].Beijing: Tsinghua University Press, 1982: 50-52.
[5] REID R C, PRAUSNITZ J M, SHERWOOD T K.The properties of gases and liquids[M].New York: McGraw-Hill, 1977.
[6] DAUBERT T E, DANNER R P.Phase equilibria in systems containing water[M].Washington: American Petroleum Institute, 1983.
[7] 普劳施尼茨 M 约翰, 利希滕特勒 N 吕迪格, 德阿泽维多 埃德蒙多 戈梅斯.流体相平衡的分子热力学[M].陆小华, 刘洪来, 译.北京: 化学工业出版社, 2006.PRAUSNITZ M J, LICHTENTHALER N R, de AZEVEDO E G.Molecular thermodynamics of fluid-face equilibria[M].LU Xiaohua, LIU Honglai, Trans.Beijing: Chemical Industry Press, 2006.
[8] PEDERSEN K S, THOMASSEN P, FREDENSLUND A.Adjustment of C7+-molecular weights in the characterization of petroleum mixtures containing heavy hydrocarbons[R].SPE 16036, 1987.
[9] TWU C H, COON J E, BLUCK D.Equations of state using an extended Twu-Coon mixing rule incorporating UNIFAC for high temperature and high pressure phase equilibrium predictions[J].Fluid Phase Equilibria, 1997, 139(1/2): 1-13.
[10] MICHELSEN M L, KISTENMACHER H.On composition-dependent interaction coefficients[J].Fluid Phase Equilibria, 1990, 58: 229-230.
[11] 廉黎明, 秦积舜, 刘同敬, 等.修正混合规则的BWRS 型状态方程及其在CO2-原油体系相态计算中的应用[J].中国石油大学学报(自然科学版), 2013, 37(2): 1-8.LIAN Liming, QIN Jishun, LIU Tongjing, et al.A BWRS type EOS based on modified mixing rule and its application in phase behavior of CO2-crude system[J].Journal of China University of Petroleum, 2013, 37(2): 1-8.
[12] SOAVE G.Equilibrium constants from a modified Redlich-Kwong equation of state[J].Chemical Engineering Science, 1972, 27(6): 1197-1203.
[13] REDLICH O, KWONG J N S.On the thermodynamics of solutions V: An equation of state[J].Chemical Reviews, 1949, 44(1): 233-244.
[14] PENG D Y, ROBINSON D B.A new two-constant equation of state[J].Ind.Eng.Chem., 1976, 15 (1): 59-64.
[15] 郭天民.多元气-液平衡和精馏[M].北京: 石油工业出版社, 2002.GUO Tianmin.Equilibria of multiple vapor/liquid and rectification[M].Beijing: Petroleum Industry Press, 2002.
[16] MELHEM G A, SAINI R, GOODWIN B M.A modified Peng-Robinson equation of state[J].Fluid Phase Equilibria, 1989, 47(2): 189-237.
[17] 秦积舜, 李爱芬.油层物理学[M].东营: 石油大学出版社, 2006: 37-61.QIN Jishun, LI Aifen.Petro-physics[M].Dongying: China University of Petroleum Press, 2006: 37-61.
[18] RACHFORD H H Jr, RICE J D.Procedure for use of electronic digital computers in calculating flash vaporization hydrocarbon equilibrium[R].SPE 952327, 1952.
[19] 廉黎明, 秦积舜, 杨思玉, 等.二氧化碳驱数学模型研究进展及发展方向[J].石油勘探与开发, 2013, 20(2): 77-82.LIAN Liming, QIN Jishun, YANG Siyu, et al.Research progress and development directions of mathematical models in CO2flooding[J].Petroleum Geology and Recovery Efficiency, 2013, 20(2): 77-82.
[20] 傅鹰.化学热力学导论[M].北京: 科学出版社, 2010: 118-129.FU Ying.Introduction of chemical thermodynamics[M].Beijing: Science Press, 2010: 118-129.
[21] 高云丛, 赵密福, 王建波, 等.特低渗油藏CO2非混相驱生产特征与气窜规律[J].石油勘探与开发, 2014, 41(1): 79-85.GAO Yuncong, ZHAO Mifu, WANG Jianbo, et al.Performance and gas breakthrough during CO2immiscible flooding in ultra-low permeability reservoirs[J].Petroleum Exploration and Development, 2014, 41(1): 79-85.
[22] 杨思玉, 廉黎明, 杨永智, 等.用于CO2驱的助混剂分子优选及评价[J].新疆石油地质, 2015, 36(5): 555-559.YANG Siyu, LIAN Liming, YANG Yongzhi, et al.Molecular optimization design and evaluation of miscible processing aids applied to CO2flooding[J].Xinjiang Petroleum Geology, 2015, 36(5): 555-559.
[23] 王佳, 丁洁丽.Logistic 回归模型中参数极大似然估计的二次下界算法及其应用[J].数学杂志, 2015, 35(6): 1-12.WANG Jia, DING Jieli.Quadratic lower-bound algorithm for maximum likelihood estimator of logistic regression on parameter and its application[J].Journal of Mathematics, 2015, 35(6): 1-12.
(编辑 郭海莉)
An improved vdW-type component mixing-rule applied in CO2-crude system
YANG Siyu1, 2, 3, LIAN Liming1, 2, 3, LI Shi1, 2, 3, YANG Yongzhi1, 2, 3, CHEN Xinglong1, 2, 3
(1.State Key Laboratory of Enhanced Oil Recovery, Beijing 100083, China; 2.National Energy (Experiment) Research Centre of CCUS, Beijing 100083, China; 3.Department of Enhanced Oil Recovery, PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China)
Abstract:A new vdW-type mixing-rule has been proposed considering the interaction among the affecting factors of temperature, pressure and non-hydrocarbon components, through analysis of equation of state and theory of interaction among molecules.By the derivation of the formulation at reduced state, a new mixing-rule has been established for the conditions of high pressure and high temperature.The theoretical strictness of the rule has been demonstrated through reducing to the dependency relationship of second virial coefficients.With the in situ petroleum samples data of vapor and liquid phase components from actual measurement, comparison has been taken between the calculation precisions of components and densities parameters calculated by the new rule and the old one.The new mixing-rule has a better accuracy to meet the industrial requirement, and its calculation is also simplified.The weighted mean error of components calculation declines from 15% to 4% and that of density calculation from 10% to 3%.
Key words:CO2-crude system; state equation; mixing-rule; reference state; flashing calculation; fugacity equation
中图分类号:TE357.45
文献标识码:A
文章编号:1000-0747(2016)03-0442-06
DOI:10.11698/PED.2016.03.15
基金项目:国家油气重大专项“CO2驱油与埋存油藏工程技术及应用”(2016ZX05016-001);中国石油天然气股份有限公司专项“长庆油田低渗透油藏CO2驱油与埋存关键技术研究应用”(2014E3606)
第一作者简介:杨思玉(1972-),女,江苏连云港人,博士,中国石油勘探开发研究院高级工程师,现从事油田气驱开发方面的研究工作。地址:北京市海淀区学院路20号,中国石油勘探开发研究院石油采收率研究所,邮政编码:100083。E-mail: yangsiy@petrochina.com.cn
收稿日期:2015-07-10 修回日期:2016-03-10

