基于单向函数的伪随机产生器与通用单向哈希函数

郁　昱， 李祥学

(1.上海交通大学 计算机科学与工程系, 上海 200240;2.华东师范大学 计算机科学与技术系, 上海 200241;3.西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)

基于单向函数的伪随机产生器与通用单向哈希函数

郁昱1， 李祥学2,3

(1.上海交通大学 计算机科学与工程系, 上海 200240;2.华东师范大学 计算机科学与技术系, 上海 200241;3.西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)

摘要:重点回顾基于单向函数的伪随机产生器，以及通用单向哈希函数的研究现状，介绍相关研究的最新进展，并对通用单向哈希函数设计方法给出系统性阐述。单向函数蕴涵伪随机产生器是密码学中的基础问题，是现代密码学的基础。单向函数可以用来构造伪随机产生器进而构成流密码算法，或是在伪随机产生器的基础上进一步构造伪随机函数和伪随机置换从而用作分组加密算法。随机迭代技术被提出并经精练后，可用于基于规则单向函数的伪随机产生器设计。单向函数蕴涵通用单向哈希函数是现代密码学最核心的基础理论之一。 关于通用单向哈希函数可以基于任意单向函数构造而来。通用单向哈希函数的应用包括基于最小假设的数字签名、Cramer-Shoup加密体制、统计隐藏承诺体制等。

关键词:密码学;单向函数;伪随机产生器;通用单向哈希函数

在现代密码学中，密码方案的设计建立在合法参与者与敌手之间计算复杂度的差异之上:对于合法的参与者，算法是可以高效执行的;对于非法参与者，算法总是计算不可行的。单向函数(one-way function,OWF)正是一类如此定义的函数，它们易于求解，但难于求逆。单向函数与随机性理论是现代密码学的主要理论基础之一，几乎所有密码机制的实现都需要许多“高质量的随机性”。以较低代价生成、交换和共享大量的“高质量的随机比特”是密码学的重要研究内容。其典型研究可追溯至Goldreich、Goldwasser、Micali、Luby、Rackoff等著名学者的早期工作。

单向函数的存在性是密码学的最基本假设，也是绝大多数对称密码学(symmetric-key cryptography)算法的充分必要条件。作为一个计算复杂性问题，单向函数可以用来构造伪随机产生器(pseudorandom generator,PRG)进而构成流密码(stream cipher)算法，或是在伪随机产生器的基础上进一步构造伪随机函数(pseudorandom functions)和伪随机置换(pseudorandom permutation),从而用作分组加密(block cipher)算法。现有的基于单向函数的伪随机产生器构造存在着构造复杂、种子长度超线性和证明规约松散等问题，使得这些构造仅限于理论研究价值，不具备实际的应用价值。

单向函数蕴涵伪随机产生器是密码学中的核心问题之一[1]，在此基础上发展了现代密码学。该问题最早可以回溯到上世纪80年代早期Blum、Micali[2]和Yao[3]分别独立发现的结论：一个PRG(通常称之为BMY产生器)可以从一个单向置换高效地构造出来。换言之，给定一个关于n比特输入的单向置换f和它的硬核谓词(hardcore predicate)hc(比如Goldreich和Levin的构造[4]),只需要调用f一次就可以得到一个伪随机产生器

g:x→ (f(x),hc(x))，

其延展度(stretch)为Ωlog(n)，并可通过重复迭代技术推广至任意延展度。这可由一个混合论断(hybrid argument)得到证明。然而,BMY产生器无法直接应用到一个任意的单向函数，因为f输出的熵可能太小而无法安全地用于之后的迭代过程。

本文将回顾基于单向函数的伪随机产生器研究现状，介绍伪随机产生器的最新研究进展。另外，单向函数蕴涵通用单向哈希函数(universal one-way Hash function, UOWHF)是现代密码学最核心的基础理论之一，关于通用单向哈希函数可以基于任意单向函数构造而来的最主要结论是由Rompel给出的。本文还将回顾通用单向哈希函数研究现状，介绍通用单向哈希函数最新研究进展，对通用单向哈希函数设计方法给出系统性阐述。

1相关概念

定义1[通用哈希函数(universal Hash functions)][5-8]一个函数类(family)

称为一个通用哈希类(universal Hash family),如果对于任意的x1≠x2∈{0,1}n,总有

Prh←H[h(x1)=h(x2)]≤2-l。

定义2[两两独立哈希(pairwise independent hashing)]一个函数类

称为两两独立的, 如果对于任意的v∈{0,1}2m、任意的x1≠x2∈{0,1}n总有

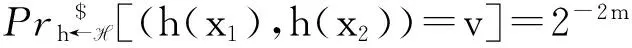
等价地，(H(X1),H(X2))与U2m同分布，其中H是H上的均匀分布。众所周知，存在可有效计算的描述长度为Θ(n+m)的两两独立哈希函数类。

定义3[单向函数(universalHashfunctions)][9-10]一个函数

f: {0,1}n→ {0,1}l(n)

是(t(n),ε(n))单向的,如果f是多项式时间可计算的,且对运行时间为t(n)的任意概率算法A,总有

Pry←f(Un)[A(1n,y)∈f-1(y)]≤ε(n)。

如果ε(n)=1/t(n),则称f是ε(n)困难的。f是一个单向函数如果存在某个可忽略函数ε(n)使得函数f是ε(n)困难的。

定义4[规则函数(regularfunctions)]一个函数f是α规则的，如果存在一个整数函数α(称之为规则度函数)，使得对于每个n∈和x∈{0,1}n,总有|f-1(f(x))|=α(n)。特别地，f是已知规则的,如果α是多项式时间可计算的;反之,则称为是未知规则的。f是已知规则(未知规则)单向函数如果f是具有已知规则度(未知规则度)的单向函数。

定义5[伪随机产生器(pseudorandomgenerators)][2-3]一个函数

g: {0,1}n→ {0,1}l(n)(l(n)>n)

是一个(t(n),ε(n))安全的伪随机产生器，如果g是多项式时间可计算的,且

CDt(n)(g(1n,Un),Ul(n))≤ε(n)。

其中(l(n)-n)是g的延展度,经常会将1n从g的参数列表中略去。称g是一个伪随机产生器,如果1/t(n)与ε(n)均是可忽略的。

定义6[弱规则(weakly-regular)单向函数][11]考虑任意单向函数

f: {0,1}n→ {0,1}l,

其值域分成集合Y1,Y2,…,Yn,其中每个Yi定义为

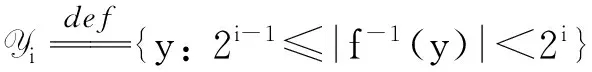
|f-1(y)|表示y的原像个数。称f是弱规则的，如果存在一个整数函数max=max(n)使得Ymax是一个显著部分(noticeableportion) n-c,其中c为一个常量,且Ymax+1,…,Yn之和所占比例是可忽略的(n)。注意到规则单向函数是弱规则单向函数的一个特例：c=0,(n)=0，max(·)为任意函数(不一定是可有效计算的)。

定义7[通用单向哈希函数][12]令

Gn={gu: {0,1}l(n)→ {0,1}l(n)-s(n),

u∈{0,1}q(n),l∈poly},

称函数类序列G={Gn}是一个(t(n),ε(n))-通用单向哈希函数，如果对每个n∈,u∈{0,1}q(n),x∈{0,1}l(n),总是可以在多项式时间内计算gu(x)，且对于每个运行时间为t(n)的概率算法A,总有

gu(x)=gu(x′)]≤ε(n)。

为简洁起见，经常使用

G={gu: {0,1}l→ {0,1}l-s,u∈{0,1}q}

表示{Gn}。

2伪随机产生器研究现状

2.1基于特殊单向函数的PRG构造

关于PRG构造的一个研究路线是使用具有特殊结构的单向函数来设计有效的PRG。早在1982年，Blum、Micali[2]与Yao[3]就分别独立地引入了PRG的概念，他们还观察到可以由单向置换(one-waypermutations,OWPs)高效地构造伪随机产生器。换言之，给定一个单向置换f和它的硬核函数(hardcore function)hc(比如由Goldreich与Levin定义的硬核函数[4]), 调用函数f一次就可以得到一个伪随机产生器g(x) = (f(x),hc(x))，其延展度(stretch，即该伪随机产生器的输入输出长度之差)为Ωlog(n)比特。基于混合论断(hybrid argument), 重复迭代技巧就可以得到任意长的延展度

gl(x)=(hc(x),hc(f1(x)),

…,hc(fl(x)),…)。

其中

我们经常将上述伪随机产生器称为BMY产生器,它具有简单、最优种子长度、最小单向函数调用次数等优点。Levin[13]注意到这里的函数f不必要一定是单向置换,只需要在其自身迭代意义上是单向的就足够了。然而，一个任意的单向函数并不具备这样的性质。

我们把一个函数称为是规则的(regular)，如果该函数的每个像都有相同个数(比如均为α)的原像。进一步，如果α是可从安全参数有效计算的话，则称该函数为已知规则的(known-regular)；反之，如果α是不能从安全参数有效近似的话，则称之为未知规则的(unknown-regular)。基于已知规则单向函数f，Goldreich、Krawczyk与Luby[14]推广了BMY产生器：通过迭代使用该单向函数、并在每两次迭代使用之间应用k-对独立哈希的技巧得到了一个在已知规则单向函数情况下种子长度为O(n3)的伪随机产生器。后来，Goldreich在他的著作[10]中给出了一个更为高效(事实上是接近最优)的基于已知规则单向函数的伪随机产生器构造：在具体安全意义下，该构造只需要调用一次单向函数即可(在一般意义下为ω(1)次)。这一构造被隐式地包含在许多HILL型的PRG设计中[15-16]。 文献[14]中使用的技巧通常被称为随机迭代方法(randomized iterate)。Haitner、Harnik与Reingold[17]对该技巧加以提炼，即

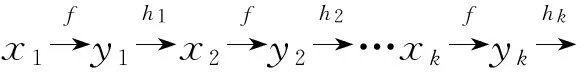
(1)

他们将该构造推广到可以适用于未知规则单向函数，且相应的种子长度缩短为O(nlogn)。 通俗地讲，随机迭代方法沿袭了文献[14]中的思路，并在每两次调用f之间使用一个随机的、两两独立的哈希函数hi，即

f(hi-1(fi-1(x;h1,…,hi-2))),i≥2。

此处关键是“最后一个迭代是难于求逆的(hard-to-invert)”[18]。当应用到hi-1(fi-1;h1,…,hi-2)后，函数f是难于求逆的,即使h1,…,hi-2,hi-1是公开的。运行该迭代O(n/logn)次、对每个迭代输出Ω(logn)个硬核比特就可以得到一个伪随机产生器,这需要的种子长度为O(n2/logn),使用Nisan的有界空间产生器(bounded-space generator[19])等去随机化技巧(derandomization techniques)可以进一步将该种子长度缩短至O(nlogn)。随机迭代技术能够达到单向函数调用次数的下界(文献[10]指出，函数调用次数的下界Ω(n/logn)同样适用于未知规则单向函数)。我们关心，是否任意高效PRG构造都能同时达到线性种子长度和Ω(n/logn)次单向函数调用呢？

文献[18]进一步对这个伪随机产生器采取了去随机化操作：使用一个程度为O(nlogn)的种子从受限空间产生器(bounded space generator,比如Nisan产生器[20])生成所有哈希函数。随机迭代技术被主要应用于基于规则单向函数的PRG构造，文献[18]也介绍了其他应用，包括基于任意指数困难规则单向函数(exponentially hard regular)的线性种子长度PRG,基于任意指数困难规则单向函数(exponentially hard regular)的O(n2)种子长度PRG,基于任意单向函数的O(n7)种子长度PRG, 以及规则弱单向函数(regular weakly-OWF)的困难性放大(hardness amplification)。

Dedic、Harnik与Reyzin[21]证明了可以减小秘密随机性的数量以得到更紧的规约,亦即,如果一个规则单向函数f有2k个像，那么，需要的秘密随机性的数量就是k(而不是n比特)。 郁昱等[22]进一步将基于任意规则单向函数的PRG的种子长度减小到O(ω(1)n)，其中ω(1)是可有效计算的。

2.2基于任意单向函数的PRG构造

Hastad、Impagliazzo、Levin与Luby等学者(HILL)关于“基于任意单向函数的伪随机产生器构造”学术工作[1]证明了“单向函数(OWFs)蕴涵伪随机产生器(PRGs)”，这一结论是现代密码学的基础理论之一。他们在文献[1]中提出的许多工具和概念,比如伪随机熵(pseudo-entropy,[23-24])和剩余哈希引理(leftoverHashlemma)，在包括抗泄漏密码(leakage-resilientcryptography)在内的其他密码学研究领域均有广泛应用。

2.3基于规则单向函数的PRG研究最新进展

郁昱等[22]重新考虑了基于规则单向函数构造伪随机产生器的问题，并设计了下述伪随机产生器。

2.3.1基于已知规则单向函数的PRG

郁昱等人使用三次提取技术[26]可以得到下述的典型伪随机产生器构造。

(1) 基于f(X)的随机性提取(randomnessextraction)。由于f(X)的最小熵为n-k,我们可以提取长度接近n-k的统计随机比特串。

(2) 基于X的随机提取。给定任意y=f(X),随机变量X有最小熵k,一次我们又可提取长度为k的统计随机比特串。

(3) 基于X的伪随机提取。经过第二次随机提取后，在给定f(X)条件下随机变量X的不可预测伪熵最多减少k。换言之，熵链原理(entropychainrule)保证了剩余的log(1/ε)比特，因此，可以使用Goldreich-Levin硬核函数[4]提取O(log(1/ε))比特。

2.3.2基于未知规则单向函数的PRG

郁昱等人也给出了一个不依赖于单向函数f规则度的构造伪随机产生器的新方法。该方法主要包括以下几个步骤。

(1) 变换为已知规则度。这里的关键思想是把任意未知规则单向函数变换为另一个特定定义域上的已知规则单向函数，亦即,对于一个保持长度(length-preserving)的未知规则(t,ε)单向函数

f: {0,1}n→Y，

其中Y⊂{0,1}n是f的值域，定义函数

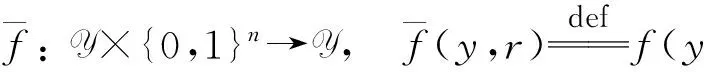
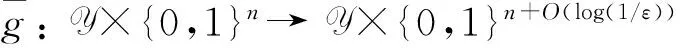
我们一般称之为Z型PRG[25]。给定输入分布Z，该伪随机产生器输出与(Z,Us)计算上不区分的(Z′,Us)，这里Z=(Y,R)，延展度s=O(log(1/ε))。注意到如果Z为U2n，则我们得到一个标准的PRG。

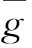
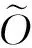
以上步骤可以改进Haitner、Harnik和Reingold[18]的使用种子长度O(nlogn)、函数调用次数O(n/logn)的随机迭代方法 (Crypto 2006)。

2.4基于弱规则单向函数的伪随机产生器

与HILL方法相比，随机迭代技术具有更短甚至几乎线性的种子长度和更紧的规约等优点，也能适用于几乎规则(almost-regular)单向函数。关于这一个推广是不难看出的(文献[17,22]中有隐式描述)。类似地，文献[11]介绍的构造也只需要“弱几乎规则单向函数(weakly-almost-regular one-way function)”，而几乎规则单向函数只是这个概念的一种特殊情况。

但是，随机重复方法是否可以进一步推广应用到比规则单向函数范围更广的单向函数呢？在此之前这还是一个公开问题，文献[11]则给出了明确的答案。作者引入了一类更广的单向函数，并使用随机迭代技术基于这种函数构造了一个种子长度为O(nlogn)、具有更紧规则的伪随机产生器。

文献[11]提出了一个称为弱规则单向函数的更为一般化的概念。具体讲,考虑一个单向函数，其值域分成集合

Y1，Y2，…，Yn,

Yi={y:2i-1≤f-1(y)<2i}。

我们称f是弱规则的如果存在一个(不必是可有效计算的)max使得Ymax构成一个显著的部分(比如n-c,c为常数),且Ymax+1,…,Yn之和仅为可忽略的。规则单向函数是弱规则单向函数的一种特殊情况：c=0,(n)=0，max(·)为不必可有效计算的任意函数。

2.4.1一个引理

郁昱等人首先从文献[18]中凝练了一个引理：如果一个算法以可忽略的概率针对均匀采样的挑战，赢得一个单项游戏(比如哈希函数的求逆),那么,当挑战是服从对数Rényi熵缺陷(logarithmicRényientropydeficiency)分布采样时，该算法的获胜概率也不会比可忽略优势更好。这里，集合W上的随机变量W的Rényi熵缺陷指的是UW的熵与W的熵之差：log|W|-H2(W), 其中UW表示W上的均匀分布，H2(W)是W的Rényi熵。

事实上，这个引理在抗泄漏密码中是隐式存在的。在其他的研究[27-29]中也有类似结论,比如针对不可区分性应用的双向游戏或者随机性是从略受污染的最小熵源采样的研究。将这个引理应用到文献[18]就可以得到该文中的关键引理的更为简单的证明：作用在规则单向函数上的任意第k次迭代是求逆困难的。其主要原因在于：即使在给定哈希函数的条件下，yk有足够大的Rényi熵，该熵只是在对数意义下略小于理想情况(即yk是f的值域上的均匀分布，并独立于哈希函数,由于单向性的原因这是求逆困难的)。

2.4.2一类更广的单向函数

郁昱等人引入了弱规则(weakly-regular)单向函数的概念。考虑任意单向函数

f: {0,1}n→ {0,1}l,

其值域分成集合Y1,…,Yn,其中每个Yi定义为

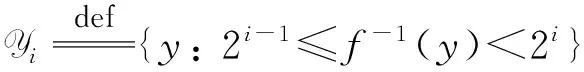
|f-1(y)|表示y的原像个数。称f是弱规则的，如果存在一个整数函数max = max(n)使得Ymax是一个显著部分(noticeable portion)n-c,其中c为一个常量, 且Ymax+1,…,Yn之和所占比例是可忽略的(n)。注意到规则单向函数是弱规则单向函数的一个特例：c=0,(n)=0，max(·)为任意函数(不一定是可有效计算的)。

2.4.3基于弱规则单向函数的PRG

文献[11]构造了一个伪随机产生器，构造过程中只需要使用到弱规则单向函数中c的知识，而不需要max和。

通俗地讲，如式(1)所示,主要想法是在第k轮迭代中，在yk∈Ymax条件下，针对给定哈希函数随机变量yk的Rényi熵接近于理想情况，即f(Un)以显著的概率并独立于哈希函数地撞入集合Ymax,而这是求逆困难的。

2.4.4几乎线性种子长度PRG

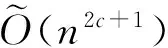
总体上看，我们的技巧与文献[18]引入的规则弱单向函数的困难性放大比较类似。读者需要注意,不要混淆弱规则(weakly-regular)与弱单向(weakly-one-way)的概念：前者的“弱”描述的是规则度(即在一个显著比例的意义上是规则的)，后者则用于单向性(即在一个显著比例的意义上求逆困难的[3])。 通俗讲,对于任意求逆算法A,一个弱单向函数有一个集合——A的失败集(failing-set)，A在这个集合上总是失败的。这样，充分多次迭代就必定会撞入每个这样的失败集以产生一个强单向函数(strongly-one-way function)，使得在一个压倒性的比例上是求逆困难的。

但是，在郁昱等人的构造中，缺少所使用函数的规则结构和那些可忽略部分Ymax+1,…,Yn进一步使分析变复杂了，他们给出了一个直观的、结构化的证明。

2.4.5关于有效性、可行性和局限性

从应用的角度看, 已知规则单向函数从以下几方面来说也许已经足够了。

(1) 如果一个单向函数的表现像一个随机函数的话,那么，它是已知(几乎)规则的。换言之, 绝大多数函数是已知几乎规则的。

(2) 在实际应用中,许多单向函数是已知规则的甚至是1-1的。 比如,Goldreich、Levin和Nisan[31]证明了1-1单向函数可以由诸如RSA和DLP这样具体的困难问题设计出来。

众所周知[10,22]，可以从已知(几乎)规则单向函数几乎最优地构造出PRG：种子长度O(nω(1))，非适应性地(non-adaptive)调用单向函数O(ω(1))次，这里ω(1)是任意可有效计算的超常数。

郁昱等人的研究切入点选择在中间阶段：引入了弱规则单向函数的概念，它位于规则单向函数和任意单向函数之间，给出了一个种子长度为O(nlogn)的PRG设计，并使用了更紧的安全规约。他们还给出关于弱单向函数与任意单向函数之间区别的讨论。

3通用单向哈希函数研究

称一个压缩哈希函数类G是通用单向的(universalone-way)，如果给定一个随机函数g∈G和一个随机的(等价地,任意预先固定的)输入x,对任意有效算法要找到任意x′≠x使得g(x)=g(x′)是不可行的[32]。单向函数蕴涵通用单向哈希函数(universal one-way Hash functions, UOWHFs)[33]是现代密码学最核心的基础理论之一。通用单向哈希函数的应用包括基于最小假设(单向函数)的数字签名[34]、Cramer-Shoup加密体制[35]和统计隐藏承诺体制(statistically hiding commitment scheme)[36-37]等。

3.1基于任意单向函数的通用单向哈希函数

3.2基于特殊单向函数的通用单向哈希函数

关于通用单向哈希函数研究的另一条路线是利用具有特殊结构的单向函数来构造更为高效的(甚至接近实用)的通用单向哈希函数。Naor和Yung提出了一种非常灵活的先哈希再截断(Hash-then-truncate)的UOWHF构造方法，其秘钥和输出长度为Θ(n)，且只需要一次调用所使用的单向置换(one-way permutation)。但是，对稍弱一些的1-1单向函数，他们只给出一个非常复杂的构造[12]。

De Santis和Yung[41]提出了一个基于任意1-1单向函数f: {0,1}n→ {0,1}l的改进设计,即

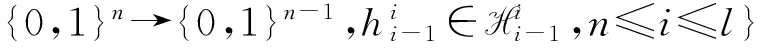
其中“∘”表示函数合成运算, 每个H表示一个两两独立的哈希函数(将i比特压缩为i-1比特)构成的函数类。虽然G1-1具有线性输出长度和仅需一次函数调用的优点，但它需要秘钥长度O(ω(logn)n)(易见G1-1需要秘钥长度O(l(l-n)),但由于每个1-1单向函数蕴涵另一个1-1(除了一个可忽略的输入部分之外)的单向函数

f′: {0,1}n′∈Θ(n)→ {0,1}n′+ω(log n),

因此,文献[12,41]中构造的秘钥长度可以压缩至O(ω(logn)n)。

表1　现有通用哈希函数构造总结对比

4.3通用单向哈希函数研究最新进展

文献[44]研究了通用单向哈希函数设计，并给出了下述一系列构造。前两个构造能够同时达到最优参数且为安全性保持的(security-preserving)：第一个通用单向哈希函数安全性与相应的单向函数是完全一样的，第二个构造的安全性是相应的单向函数的平方根。第三个构造的参数也是几乎最优的(仅相差一个任意小的超常数因子ω(1),比如log log logn甚至更小)。因此,这3个构造均是对相应的已知构造的改进。第四个构造则考虑了规则单向函数之外的情况，即文献[11]中引入的弱规则单向函数，并给出了最优输出长度Θ(n)和秘钥长度O(nlogn)的通用单向哈希函数构造。

(1) 对于任意1-1单向函数,我们构造了一个最优通用单向哈希函数类，秘钥长度和输出长度为Θ(n)且仅需一次单向函数调用。

(2) 对于任意已知困难度(known hardness)的已知规则单向函数，我们给出了另一个最优通用单向哈希函数构造，秘钥长度和输出长度为Θ(n)且仅需一次单向函数调用。

(3) 对任意已知规则单向函数，我们给出了一个通用单向哈希函数构造，秘钥长度和输出长度为O(ω(1)n)，以及ω(1)次非适应性函数调用。

(4) 对任意在定义域的显著部分(noticeable fraction,比如n-c，这里c为常数)弱未知规则单向函数f[11],我们给出了一个通用单向哈希函数构造，秘钥长度为O(nlogn)、输出长度为Θ(n)。

文献[44]的结论进一步展示了通用单向哈希函数与伪随机产生器之间的黑盒对偶性(black-box duality)[37,40,45]。首先,文献[44]抽象出了一个关于通用哈希的引理，该引理隐含在已有文献[28-29,33,37,39]之中，它在通用单向哈希函数构造中的作用与剩余哈希引理(leftover Hash lemma)在伪随机产生器构造中的作用是对等的。其次,这里的构造2和构造3匹配了基于已知规则单向函数的伪随机产生器构造中的最好结果[22],即种子长度O(ω(1)n)(如果已知单向函数的困难度的话则为Θ(n))。此外,基于同一类单向函数，构造4与文献[11]中伪随机产生器构造相对应(种子长度、秘钥长度为O(nlogn))。或许最为有趣的是,构造1与伪随机产生器情况下的非对称性：基于1-1单向函数，我们还不知道如何构造一个线性种子长度的伪随机产生器。

参考文献

[1]HASTAD J, IMPAGLIAZZO R, LEVIN L A, et al. Construction of a pseudo-random generator from any one-way function[J/OL]. SIAM Journal on Computing, 1995,28(4):12-24[2015-11-12].http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.5.7957.

[2]BLUM M, MICALI S. How to generate cryptographically strong sequences of pseudorandom bits[J/OL]. SIAM Journal on Computing, 1984,13(4):850-864[2015-11-12].http://epubs.siam.org/doi/pdf/10.1137/0213053.

[3]YAO A C C. Theory and applications of trapdoor functions (extended abstract)[C]//Proceedings of the 23rd IEEE Symposium on Foundation of Computer Science. Chicago:IEEE,1982:80-91.

[4]GOLDREICH O, LEVIN L A. A hard-core predicate for all one-way functions[C]//STOC’89 Proceedings of the twenty-first annual ACM symposium on Theory of computing. New York: ACM,1989:25-32.DOI:10.1145/73007.73010.

[5]DODIS Y, ELBAZ A, OLIVEIRA R, et al.. Improved randomness extraction from two independent sources[C]//Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques. Berlin:Springer-Verlag, 2004:334-344.DOI:10.1007/978-3-540-27821-4_30.

[6]CARTER J L, WEGMAN M N. Universal classes of Hash functions[J]. Journal of Computer and System Sciences, 1979,18(2):143-154.

[7]LEE C J, LU C J, TSAI S C, et al. Extracting randomness from multiple independent sources[J]. IEEE Transactions on Information Theory, 2005,51(6):2224-2227.

[8]STINSON D R. Universal Hash families and the leftover Hash lemma, and applications to cryptography and computing[J/OL]. Journal of Combinatorial Mathematics and Combinatorial Computing, 2002,42:3-31[2015-11-15].http://cacr.uwaterloo.ca/～dstinson/papers/leftoverhash.pdf.

[9]GOLDREICH O. Three XOR-lemmas: an exposition[C]//Studies in Complexity and Cryptography. Miscellanea on the Interplay between Randomness and Computation.Berlin: Springer-Verlag, 2011:248-272.DOI:10.1007/978-3-642-22670-0_22.

[10] GOLDREICH O. Foundations of Cryptography: Basic Tools[M/OL]. New York: Cambridge University Press, 2001[2015-11-13].http://office-for.com/lib/etc/crypto_2001.pdf.

[11] YU Y, GU D, LI X, et al. The randomized iterate, revisited-almost linear seed length PRGs from a broader class of one-way functions[C/OL]//Theory of Cryptography:12th Theory of Cryptography Conference, TCC 2015, Warsaw, Poland, March 23-25, 2015, Proceedings, Part I. Berlin:International Association for Cryptologic Research, 2015:7-35[2015-11-26].http://link.springer.com/chapter/10.1007/978-3-662-46494-6_2.

[12] NAOR M, YUNG M. Universal one-way Hash functions and their cryptographic applications[C]//JOHNSON D S. STOC’89 Proceedings of the twenty-first annual ACM symposium on Theory of computing.New York: ACM, 1989:33-43. DOI:10.1145/73007.73011.

[13] LEVIN L A. One-way functions and pseudorandom generators[J]. Combinatorica, 1987:7(4):357-363.

[14] GOLDREICH O, KRAWCZYK H, LUBY M. On the existence of pseudorandom generators[C]//Advances in Cryptology: CRYPTO’88. New York: Springer-Verlag,1990:146-162.DOI:10.1007/0-387-34799-2_12.

[15] HAITNER I, REINGOLD O, VADHAN S P. Efficiency improvements in constructing pseudorandom generators from one-way functions[C]//STOC’10 Proceedings of the forty-second ACM symposium on Theory of computing. New York: ACM, 2010:437-446.DOI:10.1145/1806689.1806750.

[16] HOLENSTEIN T. Pseudorandom generators from one-way functions: A simple construction for any hardness[C]//Theory of Cryptography: Third Theory of Cryptography Conference, TCC 2006, New York, NY, USA, March 4-7, 2006. Proceedings. Berlin:Springer-Verlag, 2006:443-461.DOI:10.1007/11681878_23

[17] HAITNER I, HARNIK D, REINGOLD O. On the power of the randomized iterate[J/OL]. SIAM Journal on Computing, 2011, 40(6):1486-1528[2015-11-20].http://epubs.siam.org/doi/abs/10.1137/080721820.

[18] HAITNER I, HARNIK D, REINGOLD O. On the power of the randomized iterate[C]//Advances in Cryptology-CRYPTO 2006: 26th Annual International Cryptology Conference, Santa Barbara, California, USA, August 20-24, 2006. Proceedings. Berlin:Springer-Verlag, 2006: 22-40.DOI:10.1007/11818175_2.

[19] HOLENSTEIN T, SINHA M. Constructing a pseudorandom generator requires an almost linear number of calls[C]//2012 IEEE 53rd Annual Symposium on Foundations of Computer Science (FOCS). New Brunswich, NJ: IEEE, 2012: 698-707. DOI:10.1109/FOCS.2012.51.

[20] NISAN N.Pseudorandom generators for space-bounded computation[J]. Combinatorica, 1992,12(4):449-461.DOI:10.1007/BF01305237.

[21] DEDIC N, HARNIK D, REYZIN L. Saving private randomness in one-way functions and pseudorandom generators[C]//Theory of Cryptography:Fifth Theory of Cryptography Conference, TCC 2008, New York, USA, March 19-21, 2008. Proceedings. Berlin: Springer-Verlag, 2008: 607-625.DOI:10.1007/978-3-540-78524-8_33.

[22] YU Y, LI X X, WENG J. Pseudorandom generators from regular one-way functions: new constructions with improved parameters[C]//Advances in Cryptology-ASIACRYPT 2013: 19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, December 1-5, 2013, Proceedings, Part II. Berlin: Springer-Verlag, 2013:261-279.DOI:10.1007/978-3-642-42045-0_14.

[23] BARAK B, SHALTIEL R, WIGDERSON A. Computational analogues of entropy[C]//Approximation, Randomization, and Combinatorial Optimization: Algorithms and Techniques: 6th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems, APPROX 2003 and 7th International Workshop on Randomization and Approximation Techniques in Computer Science, RANDOM 2003, Princeton, NJ, USA, August 24-26, 2003. Proceedings. Berlin: Springer-Verlag, 2003:200-215.DOI:10.1007/978-3-540-45198-3_18.

[24] HSIAO C Y, LU C J, REYZIN L. Conditional computational entropy, or toward separating pseudoentropy from compressibility[C/OL]//Advances in Cryptology-EUROCRYPT 2007: 26th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Barcelona, Spain, May 20-24, 2007. Proceedings. Berlin: Springer-Verlag, 2007: 169-186[2015-11-20].http://link.springer.com/chapter/10.1007/978-3-540-72540-4_10.

[25] VADHAN S P, ZHENG C J. Characterizing pseudoentropy and simplifying pseudorandom generator constructions[C]//STOC’12 Proceedings of the forty-fourth annual ACM symposium on Theory of computing. New York: ACM, 2012:817-836. DOI:10.1145/2213977.2214051.

[26] NISAN N, ZUCKERMAN D. Randomness is linear in space[J]. Journal of Computer and System Sciences, 1996, 52(1):43-53.

[27] BARAK B, DODIS Y, KRAWCZYK H, et al. Leftover Hash lemma, revisited[C/OL]//Advances in Cryptology - CRYPTO 2011:31st Annual Cryptology Conference, Santa Barbara, CA, USA, August 14-18, 2011. Proceedings. Berlin: Springer-Verlag, 2011: 1-20[2015-11-20].http://link.springer.com/chapter/10.1007/978-3-642-22792-9_1.

[28] DODIS Y, PIETRZAK K, WICHS D. Key derivation without entropy waste[C/OL]//dvances in Cryptology - EUROCRYPT 2014:33rd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Copenhagen, Denmark, May 11-15, 2014. Proceedings. Berlin: Springer-Verlag, 2014:93-110[2015-11-20].http://link.springer.com/chapter/10.1007/978-3-642-55220-5_6.

[29] DODIS Y, YU Y. Overcoming weak expectations[C/OL]//Theory of Cryptography: 10th Theory of Cryptography Conference, TCC 2013, Tokyo, Japan, March 3-6, 2013. Proceedings.Berlin: Springer-Verlag,2013:1-22[2015-11-23].http://link.springer.com/chapter/10.1007/978-3-642-36594-2_1.

[30] IMPAGLIAZZO R, NISAN N, WIGDERSON A. Pseudorandomness for network algorithms[C]//STOC’94 Proceedings of the twenty-sixth annual ACM symposium on Theory of computing.New York: ACM, 1994:356-364.DOI:10.1145/195058.195190

[31] GOLDREICH O, LEVIN L A, NISAN N. On constructing 1-1 one-way functions[C/OL]//Studies in Complexity and Cryptography. Miscellanea on the Interplay between Randomness and Computation. Berlin: Springer-Verlag, 2011:13-25[2015-11-25].http://link.springer.com/chapter/10.1007/978-3-642-22670-0_3.

[32] BARHUM K, HOLENSTEIN T. A cookbook for black-box separations and a recipe for uowhfs[C/OL]//Theory of Cryptography:10th Theory of Cryptography Conference, TCC 2013, Tokyo, Japan, March 3-6, 2013. Proceedings.Berlin:International Association for Cryptologic Research, 2013:662-679[2015-11-22].http://link.springer.com/chapter/10.1007/978-3-642-36594-2_37.

[33] ROMPEL J. One-way functions are necessary and sufficient for secure signatures[C]//STOC’90 Proceedings of the twenty-second annual ACM symposium on Theory of computing. New York: ACM, 1990:387-394. DOI:10.1145/100216.100269.

[34] GOLDWASSER S, MICALI S, RIVEST R L. A digital signature scheme secure against adaptive chosen-message attacks[J]. SIAM Journal on Computing, 1988, 17(2), 281-308. DOI:10.1137/0217017.

[35] CRAMER R, SHOUP V. Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack[J]. SIAM Journal on Computing, 2004, 33(1):167-226. DOI:10.1137/S0097539702403773.

[36] HAITNER I, NGUYEN M H, ONG S J, et al. Statistically hiding commitments and statistical zero-knowledge arguments from any one-way function[J]. SIAM Journal on Computing, 2009, 39(3):1153-1218.DOI:10.1137/080725404.

[37] HAITNER I, REINGOLD O, VADHAN S P, et al. Inaccessible entropy[C]//STOC’09 Proceedings of the forty-first annual ACM symposium on Theory of computing. New York: ACM, 2009:611-620.DOI:10.1145/1536414.1536497.

[38] ROMPEL J T. Techniques for computing with low-independence randomness[D/OL]. USA MA Cambridge: Massachusetts Institute of Technology,1990[2015-11-26].http://dspace.mit.edu/handle/1721.1/7582.

[39] KATZ J, KOO C Y. On constructing universal one-way hash functions from arbitrary one-way functions[EB/OL].[2015-11-10].http://www.iacr.org/cryptodb/data/paper.php?pubkey=12662.

[40] HAITNER I, HOLENSTEIN T, REINGOLD O, et al. Universal one-way hash functions via inaccessible entropy[C]//Advances in Cryptology - EUROCRYPT 2010: 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, May 30 - June 3, 2010. Proceedings. Berlin:Springer-Verlag, 2010:616-637. DOI:10.1007/978-3-642-13190-5_31.

[41] SANTIS A D, YUNG M. On the design of provably secure cryptographic Hash functions[C]//Advances in Cryptology — EUROCRYPT ’90:Workshop on the Theory and Application of Cryptographic Techniques Aarhus, Denmark, May 21-24, 1990 Proceedings.Berlin:Springer-Verlag, 1991:412-431.DOI:10.1007/3-540-46877-3_37.

[42] BARHUM K, MAURER U. UOWHFs from OWFs: Trading regularity for efficiency[C]//Progress in Cryptology - LATINCRYPT 2012: 2nd International Conference on Cryptology and Information Security in Latin America, Santiago, Chile, October 7-10, 2012. Proceedings. Berlin:Springer-Verlag, 2012:234-253.DOI:10.1007/978-3-642-33481-8_13.

[43] AMES S, GENNARO R, VENKITASUBRAMANIAM M. The generalized randomized iterate and its application to new efficient constructions of UOWHFs from regular one-way functions[C]//Advances in Cryptology - ASIACRYPT 2012: 18th International Conference on the Theory and Application of Cryptology and Information Security, Beijing, China, December 2-6, 2012. Proceedings. Berlin: International Association for Cryptologic Research, 2012:154-171.DOI:10.1007/978-3-642-34961-4_11.

[44] YU Y, GU D, LI X X, et al. (Almost) Optimal Constructions of UOWHFs from 1-to-1, Regular One-way Functions and Beyond[C]//Advances in Cryptology-CRYPTO 2015:35th Annual Cryptology Conference, Santa Barbara, CA, USA, August 16-20, 2015, Proceedings, Part II. Berlin: International Association for Cryptologic Research, 2015:209-229.DOI:10.1007/978-3-662-48000-7_11.

[45] GENNARO R, GERTNER Y, KATZ J, et al. Bounds on the efficiency of generic cryptographic constructions[J]. SIAM Journal on Computing, 2005, 35(1), 217-246.DOI:10.1137/S0097539704443276.

[责任编辑:陈文学]

One-way function based pseudorandom generator and universal one-way hash function

YU Yu1,LI Xiangxue2,3

(1.Department of Computer Science and Engineering, Shanghai Jiaotong University, Shanghai 200240;2.Department of Computer Science and Technology, East China Normal University, Shanghui 200241;3.National Engineering Laboratory for Wireless Security, Xi’an University of Posts and Telecommunications, Xi’an 710121)

Abstract:A survey is given to revisit the problem of basing pseudorandom generators on one-way functions, and the state of the art on universal one-way hash functions from one-way functions is reviewd.That one-way functions (OWFs) imply pseudorandom generators (PRGs) is one of the central results upon which modern cryptography is successfully founded. “The randomized iterate” technique is originally used and refined in constructing PRGs from regular OWFs. The seminal result that one-way functions (OWF) imply universal one-way hash functions (UOWHFs) constitutes one of the central pieces of modern cryptography. The principle possibility result is that UOWHFs can be based on any OWF. Applications of UOWHFs include basing digital signatures on minimal assumptions (one-way functions), Cramer-Shoup encryption scheme, statistically hiding commitment scheme, etc.

Keywords:cryptology, one-way function, pseudorandom generator, universal one-way Hash function

doi:10.13682/j.issn.2095-6533.2016.02.001

收稿日期：2015-12-25

基金项目：国家自然科学基金资助项目(61472249, 61572192, 61572149)

作者简介：郁昱(1981-),男，博士，教授，从事密码学与互联网安全研究。E-mail:yyuu@sjtu.edu.cn 李祥学(1981-)，男，博士，教授，从事密码学与互联网安全研究。E-mail: xxli@cs.ecnu.edu.cn

中图分类号：TN918.4;TP301.5

文献标识码：A

文章编号：2095-6533(2016)02-0001-11