中考反比例函数常见题型分析

黄志龙

摘 要： 反比例函数为初中函数重要内容，也是中考试卷中的必考题，其题型类型较多，学生掌握起来难度较大.为加深学生及教师对这一考点的理解与认知，作者结合历年考试内容，对中考反比例函数题型展开分析，总结其知识点.

关键词： 中考 反比例函数 题型分析函数属于初中数学重要的学习内容，其中反比例函数属于函数内容中的重要分支之一，同时也属于中考考试热点.反比例函数是对现实问题中涉及的数量关系加以刻画的数学基础模型，学生在学习这一章节内容时，在理解上容易出现偏差，部分学生对题型的把握并不准确.其实中考中涉及的反比例函数均可于课本习题中找到原型.课本习题实际是诸多专家通过反复筛选给出的具有延展性、代表性的题目，因此中学生应重视课本这一学习资料，掌握课本习题中反比例函数的提醒，以不变应万变，将掌握的解题方法用于中考反比例函数的考试中.下文笔者结合课本上的练习题，分析中考中反比例函数常见题型.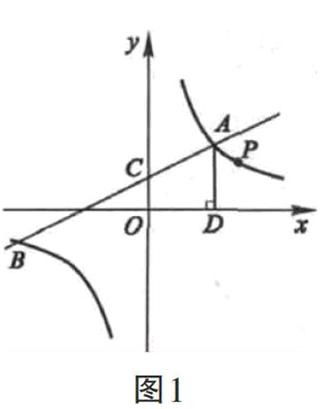

1.反比例函数和一次函数结合

中考中反比例函数和一次函数结合的这种题型比较多见，通过查阅近两年中考题，我们可发现，每个省的中考题中均会有这一题型的相关考题出现.这一类的考题可在中学课本中找到原型，具体如下：

练习题一：正比例函数y=x图像和反比例函数y=k/x的图像有一个交点，纵坐标为2，求：（1）当x=-3时，反比例函数y的值；（2）当-3

分析：从本题已知信息中可以看出，两个函数图像有一个交点，其坐标是（2，2），由此可知反比例函数k为4.在解析（1）时，将x=-3带入到反比例函数中，经解析可得y=-4/3.第（2）题在解析时，只需代入x=-1至反比例函数，可得y=-4，由此获知y的取值范围为-4

在中考中，反比例函数与一次函数结合的中考题考查的内容包括以下几点：待定系数法求解析式；求三角形面积、对函数值大小进行比较、求取函数值或自变量取值范围，等等.

我们对中考题进行分析，看怎样利用上述思路解决中考中的相关反比例函数问题.

例题1（2011年河南卷）：如图1所示，一次函数y=kx+2和反比例函数y=k/x图像，两图像在A（4，m）、B（-8，-2）处相交，和y轴交于C点.求解：（1）k与k的值；（2）根据函数图像分析，若y>y，则x的取值范围是多少？（3）过点A作AD与X轴在点D垂直，点P为反比例函数第一象限内图像中的一点，假设直线OP和线段AD在点E相交，若S∶S=3∶1，点P坐标是多少？

解析：第（1）题的答案是1/2，16；第（2）题答案或x>4或-8

因为S∶S=3∶1，所以S=1/3×12=4.故而OD·DE为4，DE为2，可得点E坐标（4，2）.由于点E位于直线OP之上，故OP解析式为y=1/2x，可得OP和y=16/x图像于第一象限内交点P坐标是（4，2）.

2.反比例函数增减性分析

练习题二：如图2是反比例函数y=（n+7）/x图像中的一支，根据图像对下述问题进行解答：（1）图像另一支所处象限是哪个象限？常数n取值范围是什么？（2）在这个函数图像的某一支上任取点A（a，b）与B（a，b），若a

这一问题的重点在于对反比例函数增减性加以考查，也即“y在x增大时增大或减小”.由于反比例函数自变量不可是0，故而其增减性并非在整个定义区域范围中得以表现，而是仅仅在每个象限中表现出增减性，这同样是中考重点考查内容.

我们选取2010年台州的一道考题进行分析：

例题2：反比例函数y=6/x图像上有三个点三者间的关系是（）

得知要研究的点并非处于同一象限内，因此不可根据“y随x增大而减小”这一规律进行判断，需通过画图将这一问题解决，因此答案应选B.

3.k几何意义分析

练习题三：下列哪个等式内y为x反比例函数？

y=4x；y/x=3；y=6x+1；xy=123

在分析时，我们需重点分析xy=123这一式子，这就需要我们对反比例函数图像知识进行学习时，主要考虑一个问题，那就是反比例函数中的比例系数k与矩形面积间的某一种联系.K几何意义为中考最常见的考点之一.

结语

通过分析我们可以看出，在平常学习中，学生应培养钻研课本习题的良好习惯，对课本习题外延、内涵认真体会，掌握反比例函数的基本题型与解题规律，应用发散性思维，这对于学生学习有重大帮助.