低温甲醇洗工艺流程模拟

蒋晓伟　汪　旭　刘　莎　潘海敏

北京石油化工工程有限公司西安分公司　西安　710075

付　强　孙　恺

陕西延长石油延安能源化工有限责任公司　榆林　71900

设计技术

低温甲醇洗工艺流程模拟

蒋晓伟*汪旭刘莎潘海敏

北京石油化工工程有限公司西安分公司西安710075

付强孙恺

陕西延长石油延安能源化工有限责任公司榆林71900

摘要本文利用PROⅡ软件中的PSRK状态方程建立低温甲醇洗工艺的全流程模拟计算，通过PSRK热力学模型中回归的二元交互作用参数及对体系液体焓值计算的修正，得到的低温甲醇工艺中各流股的温度、流量、组分及比热等模拟数据与工艺包吻合良好，且绝大部分偏差在±2%以内。整个系统的冷量偏差也仅为0.7%，修正后的PSRK状态方程应用于低温甲醇洗模拟计算，具有较高的准确性。

关键词低温甲醇洗流程模拟热力学模型

甲醇吸收CO2、H2S等酸性气体是一个物理吸收过程。即利用甲醇溶液对CO2、H2S等酸性气体能进行选择性吸收的特性来脱除合成气中的酸性气体。甲醇在加压、低温条件下对CO2、H2S、COS等酸性气体的吸收能力极强，因此，经过一次净化就能将合成气中高浓度的酸性气体清除干净，净化气质量好，净化度高。出口净化气中CO2浓度≤10ppm(v)、总硫≤0.1ppm(v)。在低温条件下，H2S的溶解度比CO2大6倍，CO2、H2S、COS在甲醇中的溶解度与CO和H2相比，至少大100多倍，而与CH4相比要大50倍。因此，H2、CO、CH4在甲醇中的溶解度都很低，再生过程中该部分有效气的损失很小[1]。

低温甲醇洗装置由于其工艺流程具有高压、低温的特点，导致气体偏离理想程度比较大，从而准确进行该工艺全流程的模拟计算具有较大难度。此外，二氧化碳在甲醇溶液中的吸收和解吸是一个强放热和吸热过程，对体系温度的计算也带来了很大的困难。由于低温甲醇洗体系内气液相平衡数据测定难度很大，且该技术作为国内外公司的专利技术，目前未曾公开发表体系相关汽液相平衡数据及二氧化碳在甲醇中的溶解热等关键数据。本文利用工艺流程模拟软件PROⅡ中的PSRK状态方程，通过对液体焓值计算等参数的修正，建立了低温甲醇洗工艺吸收流程的计算模型，不仅用于对现有生产装置提供改进建议，还可满足新建项目工程设计的需要。

1低温甲醇洗工艺流程

低温甲醇洗工艺主要由甲醇主洗塔、循环气闪蒸罐Ⅱ、H2S浓缩塔、甲醇热再生塔和甲醇水分离塔五部分组成，低温甲醇洗工艺过程流程见图1。

2状态方程模型的选择与修改

相平衡的计算有两种方法：状态方程法和活度系数法。状态方程法可以适用于压力范围较大的相平衡计算。针对混合物的相平衡进行计算，必须使用相应的混合规则。对于强极性体系和强不对称体系，状态方程法使用传统的混合规则会产生较大的误差。活度系数法通常对低压下的简单和复杂化合物都有较好的应用，而且可以预测相平衡。但是由于交互作用参数的缺少，活度系数法不适用于高压的情况。超额吉布斯自由能-状态方程(GE-EOS)模型使用活度系数GE模型计算得到混合规则，把状态方程法和活度系数法结合起来，扩大了状态方程的使用范围[2]。

Mollerup和Heidemann等[3,4]最先提出以零压力为参考态建立GE-EOS模型的思路。直到1990年Michelsen等[5～7]改进了a的函数，提出了MHV1和MHV2混合规则，以零压力为参考态的GE-EOS模型才开始广泛地应用于相平衡的计算中。MHV1和MHV2混合规则依然沿用了HV混合规则中对b使用的线性加和的方式。但是与HV不同的是，MHV1和MHV2并不限制b必须采用线性加和的求取方式，也可以选择满足第二维里系数的混合规则。

图1　低温甲醇洗工艺过程流程

在低温高压进行酸性气体吸收时，可供选择的有以下气液平衡模型：PRWS、RKSWS、PRMHV2、RKSMHV2、SR-POLAR、PSRK。这些都是基于PR或SRK立方状态方程演化来的，主要的区别是采用了不同的混合规则或者增加了对α温度函数的修正。

PSRK模型也叫预测性SRK方程，将UNIFAC(Dortmund)模型、SRK状态方程和MHV1混合规则结合起来，并将修正后的MHV1混合规则中的A1=-0.593改为A1=-0.64663，以便在较高压力下获得较好的结果。PSRK模型的修正和参数增补工作仍在进行。2000年之前，已经对PSRK模型回归了H2、CH4、N2等22种气体，200多对UNIFAC相互作用参数[8]。

为更好地计算强不对称物系的相平衡，Li等[9]将UNIFAC模型中烃分子表面积参数Q*和体积参数R*改为碳原子数的函数，对PSRK模型进行了一些改进。

R*=f(n)R

Q*=f(n)Q

f(n)=1.0-0.36983n1/2+1.0287n3/4-1.0199n+0.41645n5/4-0.05536n3/2(n<45)

此式改进提高了对小分子气体(如CH4和CO2等)在长链烃中的相平衡预测的准确性。

改进的Li-PSRK模型可提高计算强不对称物系相平衡的准确度，同时也保持了原PSRK模型计算分子大小相近物系的精度。用改进的PSRK模型计算强不对称物系相平衡的准确性优于LCVM模型。

JensAhlers 和Gmehling[10]提出一个类似于PSRK的新的GE-EOS模型。此模型基于VTPR(volume translated Peng-Robinson)状态方程，结合UNIFAC的剩余项，对b采用非线性混合规则，对非对称体系的预测有很好的改进，其结果比Li-PSRK模型好，国外专利公司采用此种方法计算低温甲醇洗。

PSRK状态方程中的参数a和b可用下式表示：

(1)

b=∑xibi

(2)

式中，A1为常数，A1=-0.64663。

(3)

式中，γi为活度系数，由UNIFAC方程求得；xi为组分i的摩尔分数，得到混合规则：

(4)

b=∑xibi

(5)

在利用状态方程计算汽液平衡时需知道混合物中各组分的分逸度系数。由SRK方程结合混合规则(4)和(5)式，可以得到混合物中组分i的分逸度系数表达式：

(6)

式中，Z为压缩因子，Z=PV/RT，β为无因次量：

(7)

高压汽液相平衡的总压和汽相组成可由相平衡方程求得：

(8)

因此，本文采用PSRK方程进行低温甲醇洗工艺的全流程模拟计算，用PROⅡ软件建立的模拟流程见(图1)。在全流程模拟时，如果不修正低温甲醇与CO2的溶解热和解析热，会导致单元温度和比热等参数产生较大偏差，未修正的CO2溶解于甲醇的溶解热计算值比实际值偏差大约在30%～40%，导致诸多冷换设备数据计算偏差较大，同时主洗塔塔顶净化气的温度比实际值要低5℃，导致系统冷量需求大幅降低，因此还需要对液体焓值作进一步修正，这一点非常重要。

3计算结果

选择600kt/a煤制甲醇装置对应的低温甲醇洗高硫工况进行分析，制冷介质为丙烯，年操作时间为8000h。利用PROⅡ软件中经修正后的PSRK模型进行模拟计算，选取其中重要流股与工艺包数据进行对比分析，其结果见表1至表4。

由上述表中可以看出，计算出的各物流流量、组分、温度、比热等参数均与工艺包数据非常接近，绝大部分偏差在2%以内，最大数据偏差在2.82%，满足工程设计需要。

选取对比缠绕式换热器负荷对比见表5。

由表5可知，计算出的缠绕式换热器负荷与工艺包给定的数据偏差很小，最大偏差约为2.5%，满足低温甲醇洗工艺设计要求，说明对甲醇与CO2的溶解热修正是合理的。

选取物流丙烯换热器冷负荷对比见表6 。

表1　低温甲醇洗涤流程重要流股主要规格对比(一)

表3　低温甲醇洗涤流程重要流股主要规格对比(三)

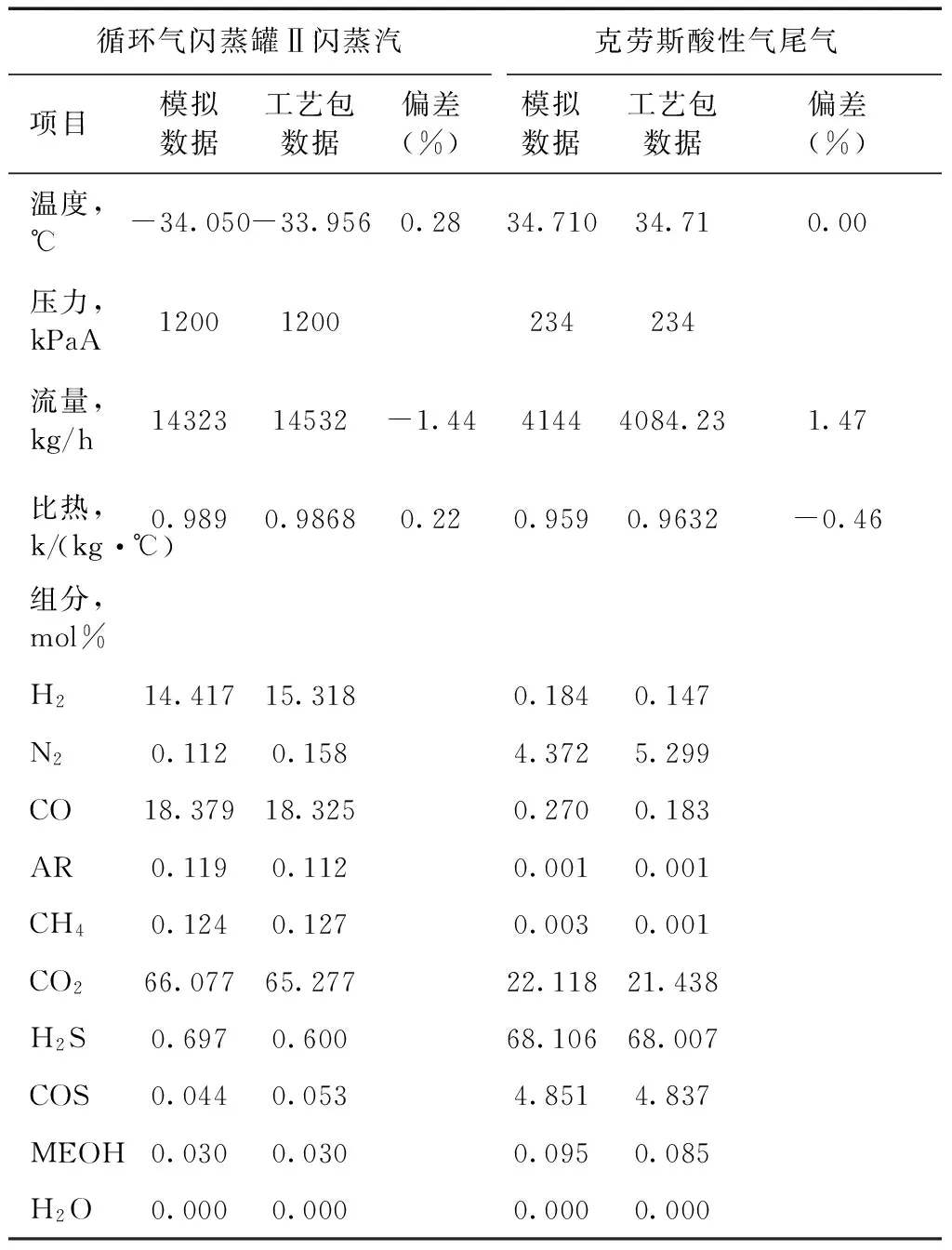
表4　低温甲醇洗涤流程重要流股主要规格对比(四)

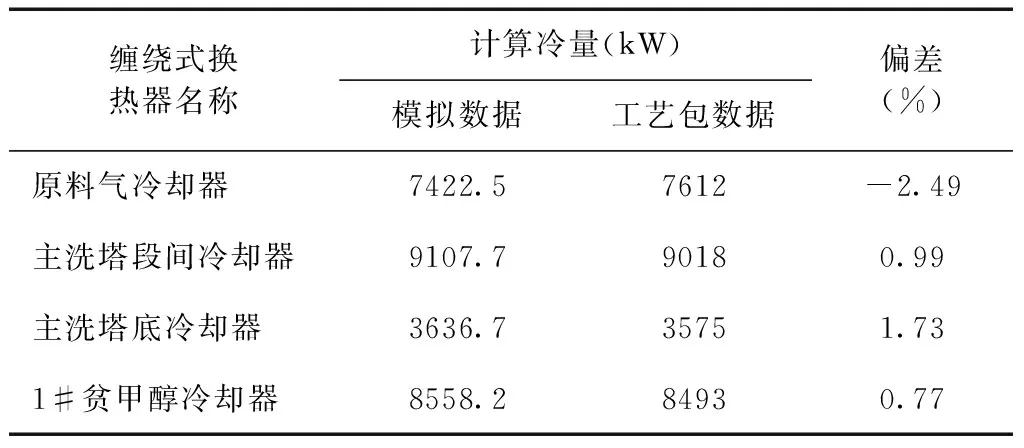
表5　低温甲醇洗涤流程缠绕式换热器负荷对比

表6　低温甲醇洗涤流程丙烯深冷器冷量对比

由表6可知，计算出的综合系统冷量(非保证值)与工艺包给定的数据仅偏差0.7%，满足低温甲醇洗配套冷冻站的工艺设计要求，可使冷冻站冷负荷的设计余量控制在合理范围内。

综合计算出的冷负荷与工艺包数据有偏差的主要原因是甲醇与CO2的溶解热偏差、循环甲醇比热偏差以及气体带出的冷量，由于-70～-20℃甲醇与CO2的溶解热焓值一直是各公司保密的范畴，故本模拟对甲醇与CO2的溶解热焓值进行了回归修订，会有一些误差，但系统合计冷负荷误差可满足工程设计需要。

4结语

(2) 本文主要采用PSRK方程，在修正液体焓值计算模型的基础上建立了低温甲醇吸收和解析酸

性气的过程模型，完成了低温甲醇洗全流程工艺模拟。模拟热力学数值结果与专利商提供的工艺包数据吻合良好，验证了该模型的可靠性，可用于类似工程的设计计算和实际生产过程的操作优化调整。

参考文献

1唐宏青.现代煤化工技术[M].北京：中国化学工业出版社，2009.

2兰雪，夏力，项曙光.超额吉布斯自由能-状态方程模型的研究进展[J].化工进展，2014，32(2)：304-308.

3MollerupJ.AnoteonthederivationofmixingrulesfromexcessGibbsenergymodels[J].FluidPhaseEquilibria, 1986, 25(3): 323-327.

4HeidemannRA,KokalSL.Combinedexcessfreeenergymodelsandequationsofstate[J].FluidPhaseEquilibria, 1990, 56: 17-37.

5MichelsenML.AmethodforincorporatingexcessGibbsenergy

modelsinequationsofstate[J].FluidPhaseEquilibria, 1990, 60(1): 47-58.

6MichelsenML.AmodifiedHuron-Vidalmixingruleforcubicequationsofstate[J].FluidPhaseEquilibria, 1990, 60(1): 213-219.

7DahlS,MichelsenML.High-pressurevapor‐liquidequilibriumwithaUNIFAC‐basedequationofstate[J].AIChEJournal, 1990, 36(12): 1829-1836.

8罗明检，马沛生，夏淑倩.超额Gibbs自由能-状态方程模型计算和预测相平衡的进展[J].石油化工，2005，34(7)：694-697.

9LiJ,FischerK,GmehlingJ.Predictionofvapor-liquidequilibriaasymmetricsystemsatlowandhighpressureswiththePSRKmodel[J].FluidPhaseEquilibria, 1998, 143(1-2): 71-82.

10AhlersJ,GmehlingJ.Developmentofauniversalgroupcontributionequationofstate. 2.Predictionofvapor-liquidequilibriaforasymmetricsystems[J].Industrial&EngineeringChemistryResearch, 2002, 41(14): 3489-3498.

(收稿日期2015-12-09)

*蒋晓伟：高级工程师。1997年毕业于西北大学精细化工专业。从事化学工程与工艺设计工作。联系电话：13379297591，

E-mail:jxw1762@126.com。