随机利率下具有红利支付的可转换债券定价

薛　红，金宇寰

(西安工程大学 理学院，西安710048)

随机利率下具有红利支付的可转换债券定价

薛红，金宇寰

(西安工程大学 理学院，西安710048)

摘要：假定股票价格遵循双分数布朗运动驱动的随机微分方程，利率满足Vasicek模型，建立双分数布朗运动环境下金融市场数学模型，利用双分数布朗运动的随机分析理论和保险精算方法，得到具有红利支付的可转换债券定价公式.

关键词：双分数布朗运动；可转换债券；保险精算；随机利率

可转换债券是指发行人依照法定程序发行、在一定时间内依据约定条件可以转换成股份的公司债券.可转债是普通公司债券和认股权证的组合，兼具债权和股权的双重属性.文献[1]假定股票遵循分数布朗运动驱动的随机微分方程，利率满足Hull-White模型，利用分数布朗运动随机分析理论与方法，得到可转换债券的定价公式；文献[2]在分数布朗运动环境下，随机利率满足Vasicek模型，得到随机利率下具有红利支付的可转换债券的定价公式.双分数布朗运动是一种比分数布朗运动更为广泛的高斯过程，可以更好的用来刻画金融资产的随机波动性，关于双分数布朗运动的概念和性质可参见文献[3-4].本文假定股票价格遵循双分数布朗运动驱动的随机微分方程，利率满足Vasicek模型，建立了双分数布朗运动环境下金融市场数学模型，利用保险精算方法，得到了具有红利支付的可转换债券定价公式.

1双分数布朗运动环境下金融市场模型

|t-s|2HK,s,t≥0,

其中：H∈(0,1),K∈(0,2)

当K=1时，双分数布朗运动就退化为分数布朗运动，当K=1,H=1/2时，双分数布朗运动就退化为标准布朗运动.

假定股票价格S(t)和利率r(t)分别满足如下随机微分方程

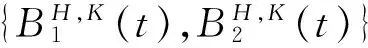
(1)

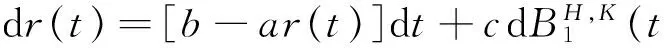
(2)

引理1 随机微分方程的解为

引理2随机微分方程(2)的解为

则

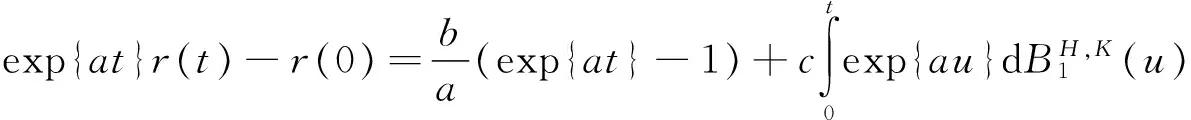
从而可证结果.

引理3[1]假定a,b,c,d,k为实数，且

ζ1～N(0,1),ζ2～N(0,1),cov(ζ1,ζ2)=ρ,

则

其中Φ(x)为标准正态分布函数.

定义6[5]股票价格{S(t),t≥0}在[0,t]上的期望回报率β(u),u∈[0,t]定义为

引理5股票价格{S(t),t≥0}在[0,t]上的期望回报率

β(u)=μ(u)-q(u),u∈[t,T]

证明由引理1可知

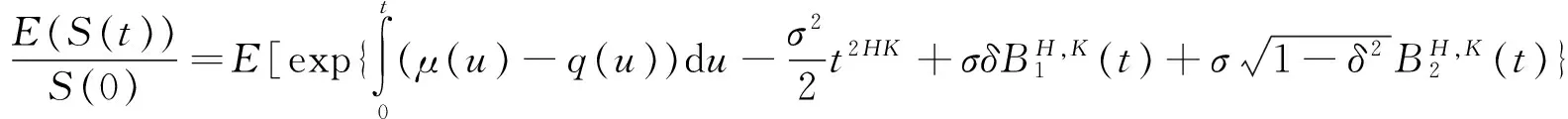
又因为

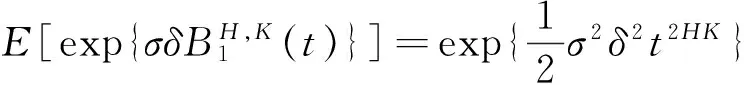
所以

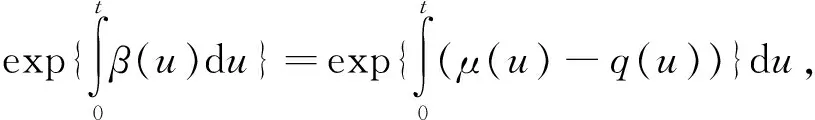
从而可得结果.

2具有红利支付的可转换债券定价

定义2 [1] 假设可转换债券只在债券到期时刻T发生转换，则可转换债券到期时的现金流量VT可以表示为

其中:VT表示可转换债券到期时刻T的价值，Pb表示纯债券价值，C表示转换价格，M表示债券面值，S(T)表示T时刻股票价格.

定义3 具有红利支付的可转换债券在0时刻的保险精算价值定义为

其中无风险资产按利率r折现，风险资产按其期望收益率β折现.

定理1具有红利支付的可转换债券在0时刻的保险精算价格

其中：Φ(x)为标准正态分布函数，且

证明令

由引理5可得

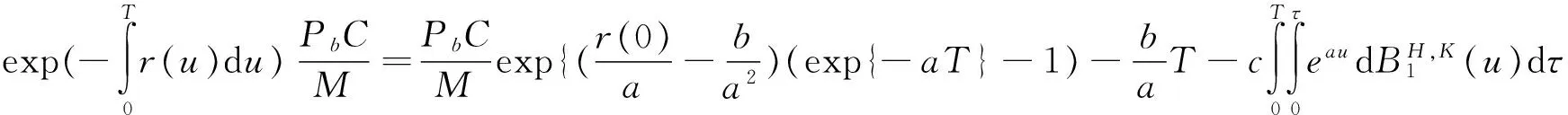
令

则A={ζ<-d},B={ζ≥-d} 又因为

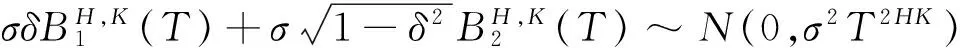
则

其中 ζ1～N(0,1),ζ2～N(0,1),且cov(ζ1,ζ2)=ε 所以

且

).

注 当K=1时，可得分数布朗运动环境下具有随机利率和支付红利的可转换债券保险精算价格(见文献[2])

其中：Φ(x)为标准正态分布函数，且

D1=σ2δ2T2H,D2=δ2(1-δ2)T2H

MH的定义见文献[6].

特别地，当K=1,δ=0,q=0时，可得文献[1]的结果.

参考文献：

[1]薛红, 李军, 吴晓蕊. 随机利率下可转换债券定价[J]. 西安工程大学学报, 2011, 25(1): 119-121.

[2]LI C, XUE H. An actuarial approach to convertible bond pricing in fractional brownian motion environment[C]// Shanghai: the 3rd International Conference on E-Business and E-Government, 2012. 2404-2407.

[3]ES-SEBAIY K, TUDOR C. Multidimensional bifractional brownian motion: Ito and Tanaka formulas [J]. Stochastics and Dynamics, 2007, 7(3): 365-388.

[4]RUSSO F, TUDOR C. On the bifractional Brownian motion [J]. Stochastic Processes and their Applications, 2006, 116(5): 830-856.

[5]BLADT M T, RYDBERG H. An actuarial approach to option pricing under the physical measure and without market assumption [J]. Insurance: Mathematical And Economics, 1998, 22(1): 65- 73.

[6]BIAGINI F, HU Y, OKSENDAL B,etal. Stochastic calculus for fractional Brownian motion and applications [M]. New York: Springer, 2008.

Pricing convertible bond with dividend paying under stochastic interest rate

XUE Hong, JIN Yu-huan

(School of Science, Xi’an Polytechnic University, Xi’an 710048, China)

Abstract：Assumed that asset price follows stochastic differential equation driven by the bifractional Brownian motion, and interest rate satisfies Vasicek interest rate model driven by the bifractional Brownian motion, the mathematical model for financial market was built. Using the stochastic analysis theory for bifractional Brownian motion and the method for actuarial mathematics, the pricing formula for convertible bond with dividend paying was obtained.

Key words：bifractional Brownian motion; convertible bond; actuary method; stochastic interest rate.

收稿日期：2015-07-02.

基金项目：陕西省自然科学基金项目(2016JM1031)

作者简介：薛红(1964-)，男，博士，教授，研究方向：随机分析与金融工程、保险精算.

中图分类号：O211

文献标识码：A

文章编号：1672-0946(2016)03-0369-03