自旋目标平动补偿与微多普勒参数估计研究

杨文革，　屈文星，　张若禹

(1. 装备学院 光电装备系， 北京 101416；　2. 装备学院 研究生管理大队， 北京 101416；3. 北京跟踪与通信技术研究所， 北京 100094)

自旋目标平动补偿与微多普勒参数估计研究

杨文革1，屈文星2，张若禹3

(1. 装备学院 光电装备系， 北京 101416；2. 装备学院 研究生管理大队， 北京 101416；3. 北京跟踪与通信技术研究所， 北京 100094)

摘要导弹目标在飞行过程中的自旋运动会对连续波雷达信号产生微多普勒调制，对调制后信号进行参数估计可获得目标的自旋频率，而目标因平动产生的多普勒频率会对微动参数估计产生影响。针对平动项引起的微多普勒频率估计参数偏移问题，通过建立同时具有平动与微动项的载波信号模型，采用延迟共轭相乘处理补偿平动项获得微多普勒信息，并通过匹配相关算法对微动参数进行估计，最后给出了该算法的具体试验步骤。仿真结果验证了该方法的有效性。

关键词微多普勒；连续波雷达；平动补偿；延迟共轭相乘；参数估计

导弹目标在飞行过程中为维持较好的定向性，会在平动的同时伴有自旋，自旋运动会在雷达回波中产生边带调制，这种现象称为微多普勒效应[1]。在连续波雷达体制下此类边带调制表现为多普勒频率上有规律的波动，其时频变化规律同目标的自旋频率相同[2]，可用于目标旋转频率的估计。

关于微多普勒频率的参数估计及提取，早期研究为便于信号处理算法的应用，均设置目标位于一固定点，平动速度为零[1-3]；而导弹目标飞行过程中会产生多普勒频偏，多普勒频偏在微多普勒参数估计中会引起微多普勒频率的折叠与偏移[4]48，从而无法获得准确的自旋频率估计值，因此在微动参数估计前应先完成平动多普勒的补偿。

文献[4]49较早地针对速度对微多普勒的影响进行了分析，该文献采用中心法对速度进行等效补偿，但所采用的频谱搬移方法并未考虑速度的多阶变化率，也未在信号层做出多普勒频率补偿。文献[5]1173采用延迟共轭相乘的方法，对信号中的平动项有较好的补偿效果，但在参数搜索中采用的Hough变换适合多分量信号处理，搜索参数计算量巨大，算法也较为复杂。文献[6]采用了基函数匹配相关搜索谱峰的方法来估计微多普勒参数，但未对调频指数进行估计，且未考虑目标平动对微动参数估计带来的影响。

本文受已有研究结果启发，提出了一种基于延迟共轭相乘和匹配相关思想的平动补偿与微多普勒参数搜索方法，并利用卡森准则与最优门限法估算信号带宽[7]355，降低了参数搜索的维度，减少了搜索算法的复杂度。仿真结果表明：该方法可实现对平动多普勒的补偿，参数估计算法较为灵活，适用于连续波雷达信号中的微多普勒参数估计。

1平动-微动复合信号模型

在目标的速度测量中常采用精度较高的非调制单频连续波，通过锁相接收回波信号获得多普勒信息。对于平动多普勒频率fT(t)可通过多项式近似表达[8]28

(1)

式中，ai为各次项系数，也为第i阶多普勒变化率；P为多普勒阶数，其各次项系数均与目标运动状态有关。自旋运动引起的微多普勒频率fmD(t)可表示为三参数的余弦函数[8]19

(2)

式中，A为微多普勒频偏；fm为目标自旋频率；φm为微多普勒初相。平动项与微多普勒频率对信号的调制作用均可看做是信号的相位调制，频率与调制相位函数之间的关系可表示为[9]

(3)

因此通过对平动多普勒频率域微多普勒频率进行积分，可得平动分量与微多普勒分量的复合信号，表示为

(4)

式中，fc为接收载频；系数bi=ai/(i+1);调频指数mf=A/fm；sc(t),sT(t),sm(t)分别为载波分量、平动多普勒分量和微多普勒调制分量。通过基带变换可得基带信号sb(t)：

(5)

2平动补偿

平动补偿可将接收信号中的平动分量进行补偿，从而提取微多普勒信号分量，在实际应用中平动补偿方法较多，根据前文分析可采用延迟共轭相乘[5]1173的方法对平动项进行补偿。补偿原理为：延迟共轭相乘处理可使信号中的平动项降阶一次，通过多阶延迟共轭相乘处理即可完成对高阶平动项的补偿。延迟共轭相乘算法可表示为

(6)

式中，τ为时间延迟量；s*(t)为原信号的共轭形式；sD(t)为延迟共轭相乘处理后的信号。因此基带信号的延迟共轭相乘函数sDb(t)可表示为

(7)

式中，sDT(t)与sDm(t)分别为平动多普勒项与微多普勒项的延迟共轭相乘函数，对两项分别展开求解。首先平动多普勒项的延迟共轭相乘函数可表示为

(8)

式中，b1,i，c1,i均为化简后的常数系数；τ为时间延迟。由于在延迟共轭相乘处理中多普勒频率最高阶ti+1得以消除，最终其sDT(t)中仅剩t的i次方项与直流分量，即一次延迟共轭相乘处理可使平动多普勒分量降低一阶。

因此平动项的k阶延迟共轭相乘函数可表示为

(9)

式中，bk,i，ck,i均为化简后的常数系数。通过P次延迟共轭相乘即可使平动多普勒多项式降低P阶，因此sDT(t)可化为

(10)

式中，t的一阶项表现为多普勒频率上的直流分量2πbP,i，在频域已不影响微多普勒频率的幅值与变化规律，只需消除此直流分量即可。根据延迟共轭相乘的性质，一阶处理可使多普勒分量降阶一次，因此需要消除一阶多普勒直流分量，要对信号再进行一次延迟共轭相乘处理。可得最终补偿后的信号为

(11)

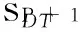
关于微多普勒调制项的延迟共轭相乘函数可表示为

(12)

式中，l1为一阶幅值增益因子；φ1为一阶相位延迟因子，可分别表示为

(13)

可看出一阶延迟共轭相乘只改变了微多普勒调频项中微多普勒频率的幅值与相位，其自旋速度并无改变。因此微多普勒项的P+1阶延迟共轭相乘函数可表示为

(14)

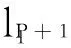
(15)

(16)

根据文献[10]的研究表明，弹道目标在飞行中段只受地球引力的作用，弹道较为平缓，平动多普勒近似为三阶多项式足够满足精度要求，即四阶延迟共轭相乘处理足以满足对平动多普勒补偿的需求。

3微多普勒信号参数估计

微多普勒信号参数估计可采用与基函数匹配相关处理，搜索谱峰的方法来完成[11]44。对平动补偿后的信号采用门限检测的方法估计信号带宽，利用卡森准则换算得调频指数，设置2项相关搜索参数分别为：旋转频率与微多普勒相位，取信号实部与基函数进行匹配相关处理并搜索谱峰，通过换算可得所估参数。

根据上一节所得平动补偿后的信号可知，现需要估计的参数有3项，分别为调频指数mfs、自旋频率fm与微多普勒初始相位φms。由于对3项参数同时搜索，迭代次数多，搜索谱峰算法复杂。因此需要对调频指数进行换算，由卡森(Carson)公式[12]可换算得调频指数为

(17)

式中，B为调频信号带宽。采用带宽采样门限检测的方法可较为方便准确地估计出信号带宽，并将搜索维度降低为二维，很大程度上减少了相关运算的次数，降低了谱峰搜索的难度。

关于门限检测法估计信号带宽的算法流程如下[7]354：

1) 对待估信号进行FFT运算计算其频谱，并对频谱做归一化处理。

2) 寻找最大谱峰与次大谱峰，记其谱峰归一化幅值分别为E1与E2，计算能量比η=E2/E1。根据能量比η判断此调频信号为弱调制还是深度调制(根据经验值可知当η<1时，信号为弱正弦调制，否则为深度正弦调制)。

3) 当判断信号为深度正弦调制后，设置检测门限μ，统计频谱归一化幅度高于检测门限的频率，取极值频率之差即为估计所得带宽B，通过多次测量剔除大于平均值的野值点。由于白噪声对信号频谱的影响常表现为边带频率，因此检测门限μ应随着信号载噪比环境的优劣性而随之改变。

结合式(17)构建搜索基函数

(18)

(19)

(20)

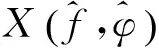
(21)

其在有限时间T内的数字信号形式可表达为

(22)

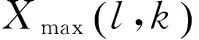
由于在做延迟共轭相乘处理时，改变了微多普勒信号的调频指数mf与初相φm，因此在构建微多普勒补偿函数前，需对搜索到的参数进行缩放与移相处理。

(23)

由于在P阶延迟共轭相乘处理中对信号进行过无用信息的截除，截除处理改变了理论相位的初始位置，因此在计算实际微多普勒初始相位时应做相位补偿。截除均为从0时刻开始，分P次共截取Pτ(单位为s)的无用信息，此段时长内的信号相位变化量为

(24)

(25)

4仿真试验与分析

4.1平动补偿

设置信号时长为4 s，目标自旋频率0.5 Hz，微多普勒频偏40 Hz，微多普勒初始相位为π/3，根据标准测控信号取信噪比为20dB[13]，一阶多普勒变化率500Hz，通过式(4)可得多普勒理论时频特征。

对信号S(t)做短时傅里叶变换(Short-TimeFourierTransform,STFT)，可得基频信号时频特征，如图1所示。

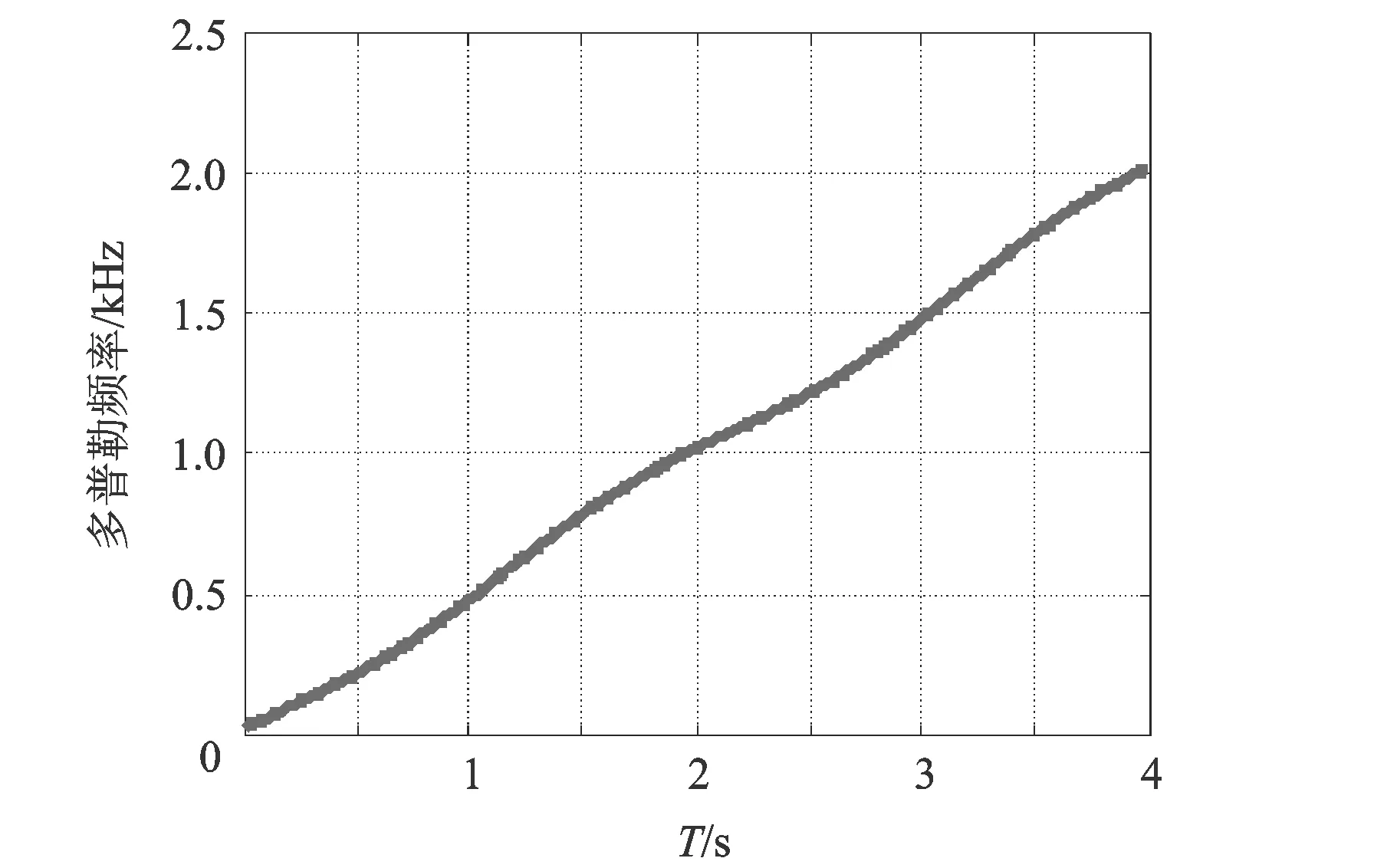
可看出STFT变换结果与理论时频特征是一致的，微多普勒频率表现为多普勒频率上有规律的波动。取延迟量τ=0.5s，进行二阶延迟共轭相乘处理，并对处理后的无用信息做截除，其补偿结果如图2所示。

从图2a)中可以看出微多普勒频率表现为以固定频率为中心的周期性波动，说明一阶延迟共轭相乘处理已补偿多普勒频率的一阶分量。

从图2b)中可看出二阶延迟共轭相乘处理已将信号中的固定频率予以补偿，微多普勒频率已被搬移至零频。仿真结果与前文分析结果是一致的，满足微动参数估计的条件。

a) 理论时频特征

b) STFT变换结果图1　基频信号多普勒时频特征

a) 一阶延迟共轭相乘处理

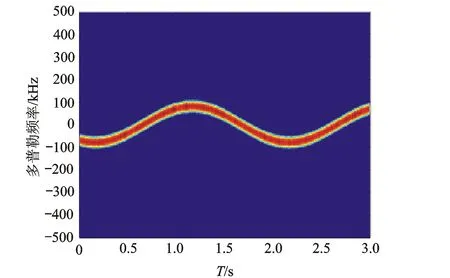
b) 二阶延迟共轭相乘处理图2　平动补偿信号时频特征

4.2微多普勒参数搜索

根据上文分析通过对调频指数的换算可减少参数搜索的维度以及运算复杂度，因此首先对平动补偿后的信号带宽进行估计，其带宽如图3所示。之后设置自旋频率搜索范围为0～2Hz，微多普勒相位搜索范围为0～2π，整体搜索步长为1/100，结合式(22)进行参数搜索，结果如图 4所示。

图3　平动补偿后的信号频谱

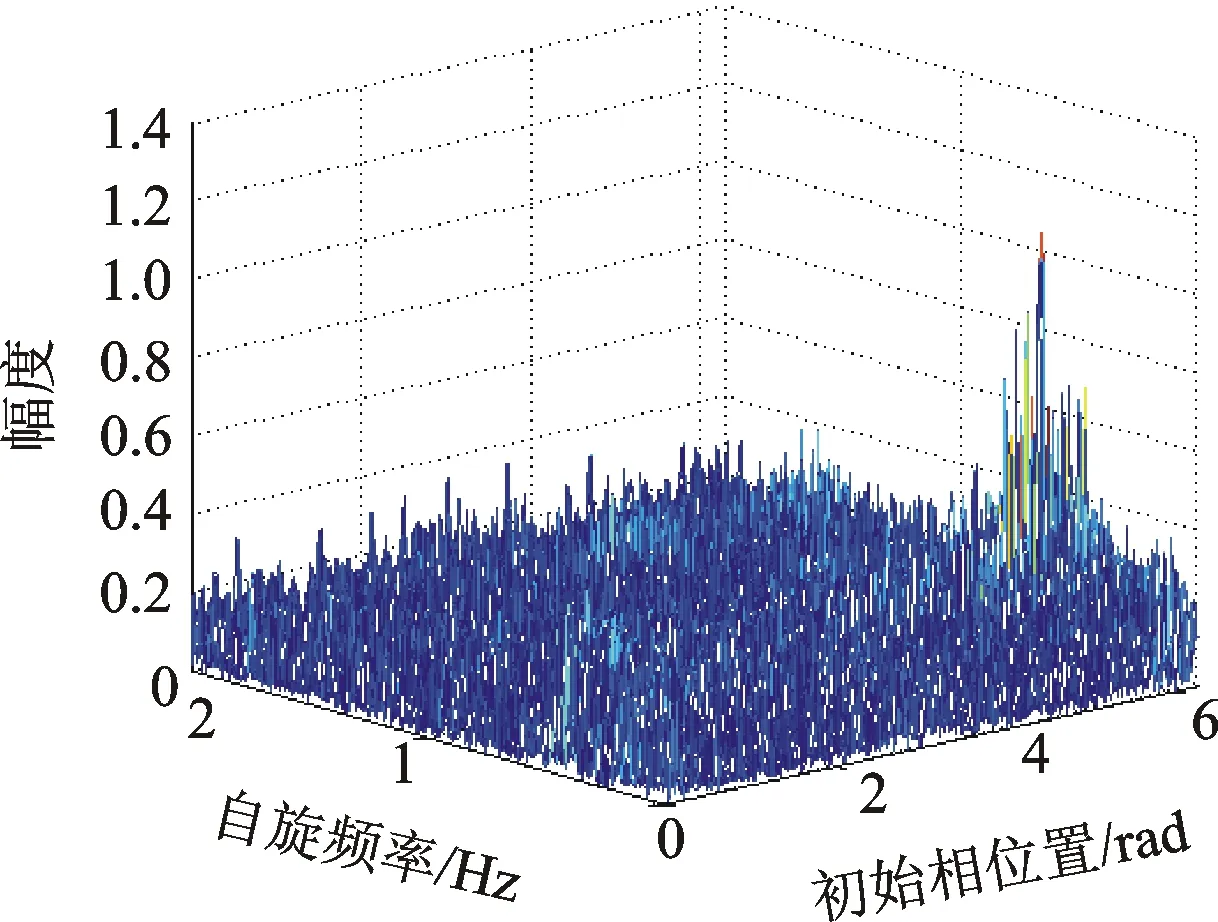
图4　微多普勒信号参数搜索结果

通过频谱门限过滤与谱峰搜索，结合式(20)、式(23)与式(25)可计算对应的微多普勒频偏、自旋频率与微多普勒相位。其结果与真实参数与未进行平动补偿的估计结果进行比较，如表 1所示。

表1　微多普勒参数估计结果比较

可看出对未进行平动补偿的信号进行参数估计，其估计值与真值出现了较大的偏差，而本方法通过延迟共轭相乘处理，完成了平动多普勒的补偿，所估参数精度得到了较大改善。

本算法结合卡森准则进行微多普勒信号带宽估计，根据式(20)可得本文方法的乘法运算复杂度Ca为

(26)

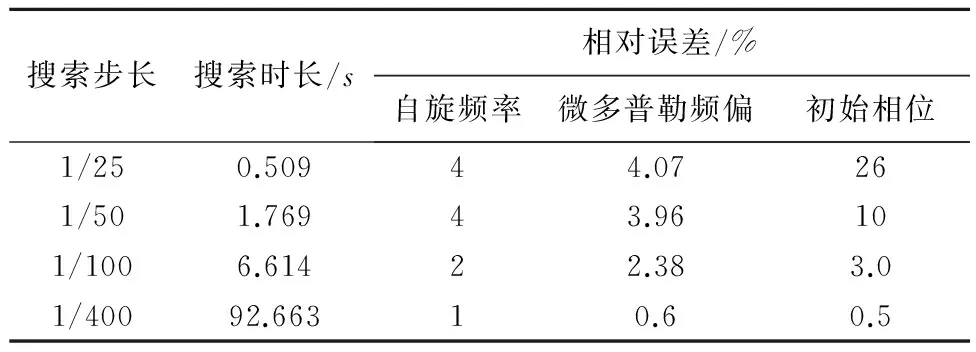
式中，M为单参数循环次数；K为复杂度系数；N为信号采样点数；KN为单次匹配相关乘法运算次数；NF为FFT点数；相比文献[11]51中对微多普勒参数的三维搜索，本算法运算复杂度减少MKN-NFlbNF，其中NF<

为验证不同搜索步长下的参数估计效果，分别设置搜索步长为1/25，1/50与1/400进行参数搜索，可得不同搜索步长下的估计精度，如表 2所示。

表2　不同搜索步长下的参数搜索时长与

可看出当搜索步长较大时，估计误差较大；反之步长较小时，估计误差随之减小。虽然短步长条件下估计误差小，所估参数可取较高的精度，但搜索时间相比其他搜索补偿较大，因此在实际应用中通过结合测量精度与运算时间的需求来权衡步长的选择。

5结 束 语

针对平动对旋转目标微多普勒参数估计带来的频率偏移问题，本文基于连续波雷达体制，通过延迟共轭相乘的方法完成了对信号平动分量的补偿，对微多普勒信号采用相关匹配的方法实现了微多普勒参数的估计，并给出了仿真试验的具体步骤。仿真结果表明：该方法搜索维度低，算法原理简单且易于实现，在搜索步长为1/400时，各项参数估计值的相对误差均能控制在1%以下，适用于动目标的微动参数估计。但在较低信噪比环境或其他干扰环境下(如常见的多径干扰)，如何完成平动多普勒的补偿与微动参数的估计，仍需结合实际情况对搜索步长的选择进行更好的权衡，进一步完善估计算法。

参考文献(References)

[1]CHENVC,LIF,HOSS,etal.Analysisofmicro-Dopplersignatures[J].IEEEProc.RadarSonarNavig,2003,150(4):271-276.

[2]屈文星，杨文革，张若禹．应答式旋转目标的微多普勒研究[J]．电子测量技术,2015，38(11):32-36．

[3]CHENVC,LIF,HOSS,etal.Micro-Dopplereffectinradar:phenomenon,model,andsimulationstudy[J].IEEETransactionsonAerospaceandElectronicSystems,2006,42(1):2-20.

[4]高红卫，谢良贵，文树梁，等．速度对微多普勒的影响及其补偿研究[J]．航天电子对抗，2008(4)：46-50．

[5]杨有春，童宁宁，冯存前，等．弹道中段目标回波平动补偿与微多普勒提取[J]．中国科学：信息科学，2013(9)：1172-1182．

[6]李宝柱，袁起，何佩琨，等．目标自旋引起微多普勒的补偿新方法[J]．现代雷达，2008(10)： 49-51．

[7]熊辉，吕远，曾德国，等．利用卡森准则的正弦调频信号参数估计方法[J]．电子测量与仪器学报，2010，24(4)：353-358．

[8]刘进.微动目标雷达信号参数估计与物理特征提取[D].长沙:国防科学技术大学,2010:19-28.

[9]ZHAOY,WANGG,BAIY.AnewmethodoftranslationalcompensationforspacespinningtargetbasedonEMD[C]// 2013IEEEInternationalConferenceonSignalProcessingCommunicationandComputing.Kunming：IEEE,2013:1-5.

[10]陈行勇．微动目标雷达特征提取技术研究[D]．长沙:国防科学技术大学,2006:131-132.

[11]魏萌.微多普勒效应分析及参数提取[D].成都:电子科技大学,2010：44-51.

[12]樊昌信，曹丽娜．通信原理[M]．北京：国防工业出版社，2008：109-110.

[13]李伟,杨文革,赵江.基于VFD滤波器的测控信号动态信息加载方法[J].现代防御技术,2015,43(3):146 -150.

(编辑：李江涛)

Research on Translational Motion Compensation and Micro-Doppler Parameter Estimation of Spinning Target

YANG Wenge1,QU Wenxing2,ZHANG Ruoyu3

(1. Department of Optical and Electronic Equipment, Equipment Academy, Beijing 101416, China;2. Department of Graduate Management, Equipment Academy, Beijing 101416, China;3. Beijing Institute of Tracking and Telecommunication Technology, Beijing 100094， China)

AbstractThe spinning motion of flying missile will produce micro-Doppler modulation on continuous wave radar echo signal. Parameter estimation for this modulated signals will obtain the spinning frequency of the target and the Doppler frequency of translational motion will have influence on the estimation of the micro parameters. Aiming at the problem of deviation of estimation on the micro-Doppler frequency parameter, through building up a carrier signal model with translational motion and micro-motion items , the paper obtains the information of the micro-Doppler by compensating translational motion with delayed conjugated multiplication, then estimates the micro motion parameters by matching relevant algorithm, and finally concludes the specific steps of this algorithm. The simulation result verifies the effectiveness of this method.

Keywordsmicro-Doppler; continuous wave radar; translational motion compensation; delayed conjugated multiplication; parameters estimation

收稿日期2015-12-01

作者简介杨文革(1966-)，男，教授，博士生导师，主要研究方向为航天测控。

中图分类号TN959.6

文章编号2095-3828(2016)03-0107-06

文献标志码A

DOI10.3783/j.issn.2095-3828.2016.03.021