高速公路建设期突发事件协同救援模型研究

张勤

摘 要：鉴于高速公路本身及其建设期施工的特点，建立高速公路建设期突发事故基于应急救援行程时间、机会成本、单位时间经济损失的应急协同管理模型，降低事故救援救援成本。同时将问题模型转化为运筹学中指派问题并用匈牙利算法对问题进行求解。实现高速公路建设期对突发事件快速反应，最小经济损失的资源协同救援的目的。

关键词：高速公路；建设期；突发事件；协同救援模型

中图分类号：U459.2 文献标识码：A 文章编号：1006-8937（2016）02-0041-03

高速公路是固定在广阔地域上的线形建筑，不能移动。同时高速公路建设期施工具有高空作业、地下作业、流动作业等突出特点，安全事故频频发生。这就要求根据实际需要提供多次应急救援服务的问题。协同的核心就是打破资源间的壁垒和边界使系统优化，为共同的目标而进行协调的运作[1]。

1 问题的引入

该模型是主要针对高速公路建设期突发事件应急救援，从三种情况分析不同影响因素对救援决策的影响。

1.1 情况一及问题

情况一：考虑突发事件到救援点的时间，如图1所示。

问题描述如下：若分段W7、W8之间发生1起突发事件b1，事件b1位于分段W8，但b1离应急救援点a7较近，按照就近原则，应派a7的救援车到b1事故现场进行应急救援。从这种情况可以看出，应急救援策略的选择与应急救援行程时间T有密切的联系[2]。

1.2 情况二及问题

情况二：考虑机会成本，仍如图1所示。

机会成本指在高速公路应急救援时，负责某路段的应急救援车辆离开了自己的路段去处理其他路段事故，就没有应急救援车辆来覆盖该路段。如果该路段发生突发事件，将没有资源对其进行紧急救援，由于没有及时救援所造成的经济损失值，就称为该路段的机会成本[3]，用字母D表示。

若对于情况一考虑机会成本。如果应急救援点a7所负责的路段有难度较大的桥梁和隧道施工并经常发生突发事件，很可能当a7离开自己所负责的路段来处理突发事件b1，在这段时间里，a7负责的路段发生重大事故，即a7负责的路段的机会成本值大于a8所负责路段的机会成本值。从这个角度分析可以得出应急救援策略的选择与机会成本D之有密切的联系。

1.3 情况三及问题

情况三：考虑突发事故的严重程度，如图2所示。

如果分段W8发生了同时突发不同等级的事件b3 、b4其中b4比b3严重。根据情况一应由a8救b3而不是a7救b3，但急需救援的b4而言a9距事故b4比a8更远。考虑救援行程时间则应选择a8的救援车救b3、a9的救援车救b4，但对于急需救援的b4，a9距离b4比a8更远。从这种情况可以得出应急救援方案的选择与事故发生的严重性即事故每分钟的经济损失U有密切的联系。

从上面的三种情况可以看出，高速公路建设期应急救援方案的选择跟应急救援行程时间T、机会成本D和每分钟经济损失U三个因素密切相关。

2 模型因素定量分析

2.1 应急救援行程时间T的计算

应急救援行程时间用下式表示：

T=L/V

其中，L表示应急救援车辆到突发事件发生点的路段长度；

V表示救援车辆的速度。

应急救援车辆到达事故现场的速度受现有路网的情况、施工便道长度、施工便道车道数、天气情况及路面状况等方面因素的影响。

2.1.1 周围路网的车速度

高速公路的周围路网应急救援车辆的速度，主要是通过实时的交通检测器检测的数据来确定[4]。

这个算法可用以下模型表示：

2.1.2 施工便道的车辆速度

由于施工便道是临时搭建，道路等级低，设计指标差以及路面结构多为泥结碎石路面。不能采用交通信息采集系统的方法检测，通常采用雷达测试枪获取各施工便道平均车速。

2.2 机会成本D的计算

2.2.1 高速公路分段

通过分析大量高速公路建设期突发事件，从中找出其空间、时间分布以及突发事件经济损失等统计学规律，以便对高速公路空间性进行分段。

2.2.2 事故经济损失分级

根据《国家安全生产事故灾难应急预案》中突发事件的严重性、紧急程度和可能波及的范围，将突发事件等级分为特别重大事故（Ⅰ级）、重大事故（Ⅱ级）、较大事故（Ⅲ级）和一般事故（Ⅳ级）四级[5]。

2.2.3 机会成本

对高速公路空间合理分段，分析建设期以来的突发事件数据，得到每个分段上各时间段经济损失，并将这些经济损失值填入到经济损失表中，从而可以得到某个路段某个时间段的机会成本Pi。

2.3 单位时间经济损失U的计算

高速公路建设期突发事件不同突发事件类型带来的不同的经济损失。先将高速公路建设以来的突发事件所有事故类型及造成的经济损失提取出来，形成表格，将每一个事故分为5个严重等级，见表1。

其中，每分钟的经济损失值等于经济损失值除以突发事件关键时间长度。即：

U=P/Tkey

其中，P表示突发事件造成的经济损失值；

Tkey表示救援关键时间。

事故的发生通常有不同伤亡情况，那么可以归纳出突发事件每分钟的经济损公式：

式中：n为表示第k类突发事件的个数；

m为第k类突发事件的严重程度；

Uk为第k类突发事件的每分钟经济损失。

2.4 协同救援模型建立

根据高速公路建设期突发事件发生的实际情况以及重难点工程的分布，将高速公路分为n段。该模型只考虑每个段只有1辆应急救援车辆负责，这样共有n辆应急救援车。当某段发生1起突发事件时，综合考虑应急救援时间T、机会成本D、每分钟经济损失U，通過目标函数所追求的最小的经济损失值得到求解经济损失值的函数f（D，U，T）。这样就有n个经济损失值，选择其中经济损失值最小的那个应急救援车来处理该事件。

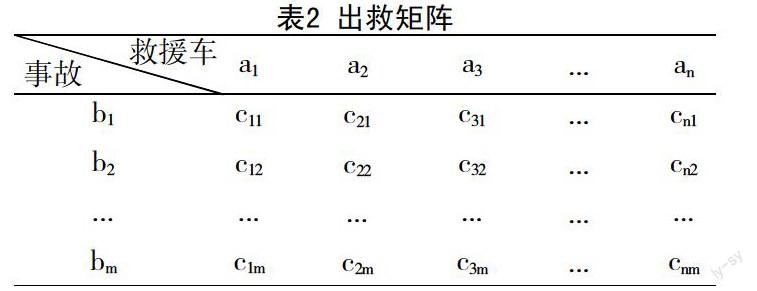
如果有m个突发事件同时发生，用bj表示突发事件，ai来表示应急救援车辆，那么每辆救援车救援该事件所产生的经济损失值为Cij=D+UT，则会将产生m个c值，将m个不同行不同列的Cij求和使？撞Cij值最小的应急救援策略就是这里所要求的最优应急救援方案。将这些Cij计算出来，形成一个出救矩阵，见表2。

设使用[cij]表示应急救援行列式，令引入变量xij；其取值只能是1或0。

xij=1，当救援车辆ai救援第j个事故时0，当救援车辆ai不救援第j个事故时

3 模型求解过程

上述问题是一个单目标最优解问题与运筹学中的指派问题一致。因此，可以运用运筹学中指派问题的方法来求解此问题。

3.1 指派问题

指派问题是0-1型整数规划的特例[6]。指派问题简述为某单位需完成n项任务，刚好有n个人可胜任这些任务，但由于每人的专长不同，效率也不同。问题的难点即应指派何人去完成何项任务，使完成n项任务的总效率最高。

3.2 匈牙利算法

匈牙利算法只适合求解行和列相等的指派问题，而且是求得极小值[6]。但是很多實际情况的指派问题与典型的指派问题的区别只是任务数与完成任务的人数不相等即行和列不相等。当然这些问题不能直接用匈牙利算法求解，但可添加虚拟变量达到匈牙利算法需要的条件。

应急救援车辆相当于指派问题当中的人，突发事件就相当于指派问题当中的任务。应急救援车n和突发事件数m是不相等时（此处只讨论m4 结 语

合理的救援策略可以减少高速公路建设期突发事件损失。本文基于应急救援时间、机会成本、单位时间经济损失救援影响定量分析建立了高速公路建设期突发事件协同救援模型。运用运筹学中指派问题对模型求解。为如何以更短时间，最少经济损失完成应急协同救援提供参考。

参考文献：

[1] 赵林度，卢雅琪.城际重大危险源应急网络协同及其经济性研究[J].中 国安全生产科学技术，2008，（5）.

[2] 吴晓涛，吴丽萍.突发事件区域应急联动影响因素的实证研究[J].灾害 学2011，（3）.

[3] 李建斌，高速公路突发事件紧急救援关键技术研究[D].西安：长安大 学，2012.

[4] 陈丽娅.高速公路事件处置消息驱动应急联动技术分析[J].技术，2013，（11）.

[5] 国家安全生产监督管理总局.国家安全生产事故灾难应急预案[J].安 全与健康，2007，（3）.

[6] 《运筹学》教材编写组.运筹学[M].北京：清华大学出版社，2004.