基于改进型最小二乘搜索的GNSS姿态测量方法

李世杰，李治安，庞春雷，刘　明

(空军工程大学 信息与导航学院，陕西 西安 710077)



基于改进型最小二乘搜索的GNSS姿态测量方法

李世杰，李治安，庞春雷，刘明

(空军工程大学 信息与导航学院，陕西 西安 710077)

摘要：结合全球卫星导航系统(global navigation satellite system，GNSS)用于姿态测量具有基线已知的特点，提出了一种改进型最小二乘搜索算法：将整周模糊度分为基本组和剩余组，在伪距精度和基线长度约束条件下确定出基本模糊度组的搜索空间；然后根据模糊度与基线俯仰角、航向角的关系，并以俯仰、航向角度组合作为联系基本组和剩余组的中间变量，通过搜索基本模糊度组来确定出剩余模糊度组合；最后利用最小二乘解算基线矢量，在二次残差比值检验条件下，完成整周模糊度的固定及姿态解算。实验结果表明，改进算法不仅有效减小了模糊度的搜索空间，而且缩短了模糊度初始化时间，具有较高的测姿精度，适用于GNSS姿态测量。

关键词：全球卫星导航系统；最小二乘搜索；整周模糊度；姿态测量；基线约束

0引言

基于全球卫星导航系统(global navigation satellite system，GNSS)的姿态测量是以整周模糊度的正确固定为前提，并通常在基线较短、长度固定已知等约束条件下完成姿态解算。最小二乘搜索算法是一种有效的模糊度解算方法[1]，其基本思想为：首先根据伪距精度确定模糊度的搜索空间，并选取其中3个作为基本模糊度组，由于所有双差整周模糊度中只有3个是相互独立的[2]，因此可以利用基本模糊度组求解出所有的模糊度组合，从而大大减小了模糊度的搜索空间。近些年，随着GNSS测姿技术的不断发展，许多学者也在研究基于最小二乘搜索的GNSS姿态测量方法。文献[3]利用基线长度约束条件并基于乔氏(Cholesky)分解减小了基本模糊度组的搜索范围，提高了搜索效率；文献[4]采用多天线测姿方法，对最小二乘搜索算法的测姿精度进行了分析；文献[5]提出了短基线约束条件下的模糊度二维搜索算法，给出了具体搜索方法，并简化了搜索模型；文献[6]提出了利用倾角传感器提供基线俯仰角，并和基线长度、卫星间几何关系等共同作为约束条件的最小二乘搜索算法，有效减小了搜索范围，缩短了模糊度初始化时间，但其需要外部传感器的辅助。综合文献[3-6]可以看出，基于最小二乘搜索的GNSS测姿算法还未充分考虑基线约束条件下的搜索域与基线长度之间的互相制约关系，基本上还是进行遍历搜索，未考虑模糊度确认方法对初始化时间的影响，效率有待进一步提高。

本文在此基础上，提出了一种新的GNSS姿态测量方法：利用伪距精度和基线长度确定基本模糊度组的搜索范围，并对其进行搜索，根据其与俯仰角和航向角对应关系，以俯仰和航向角度组合作为中间变量确定出剩余模糊度组合，不仅实现了模糊度的二维搜索、减小了搜索空间，而且充分利用了基线和角度之间的约束关系，减小了其他待搜索模糊度组合对最佳搜索组合的影响，有利于模糊度的快速确认，缩短了初始化时间；同时该算法给出了选星依据，通过确定最佳基本模糊度组，提高了算法可靠性。

1传统最小二乘搜索算法

最小二乘搜索算法是从所有双差模糊度中选取3个作为基本模糊度组，并利用模糊度之间的相关性，由基本模糊度组确定出剩余模糊度组合，从而将模糊度的搜索维数降为3维。基本模糊度组对应的双差方程可表述为[6]

(1)

(1)式中：ΔN12，ΔN13，ΔN14为基本模糊度组中的双差模糊度值；ΔL12，ΔL13，ΔL14为对应双差载波相位观测量；d为基线矢量；s1，s2，s3，s4为用户到对应卫星的观测矢量；λ为载波波长。

对基本模糊度组中所有可能的模糊度组合进行搜索，代入(1)式，解得基线矢量d，设双差整周模糊度个数为n-1(n>4)，再利用基线矢量解得剩余模糊度组ΔN1x(5≤x≤n)为

(2)

由此得到所有待搜索的模糊度组合，并通过比率检验法完成模糊度的固定。在确认出正确的双差模糊度后，利用最小二乘解算得到精确的基线矢量，并通过坐标转换得到姿态角参数。

实际上，在GNSS测姿过程中，通常还可以利用基线长度约束限制模糊度的搜索范围，进而减小基本模糊度组搜索空间。但从文献分析中可以看出， 搜索效率和初始化速度还可以进一步改善。

2新方法

2.1模型建立

图1为基线AB在东北天(ENU)坐标系的示意图。A，B分别为2个卫星天线位置，以A为原点的ENU坐标系中，由A到B的基线矢量记为d，基线长度、航向角、俯仰角分别记为d，φB和θB；卫星i的航向角、俯仰角分别记为φSi和θSi；Δφi为卫星i与基线AB的航向角之差，即Δφi=φSi-φB；si为用户到卫星i的单位矢量。

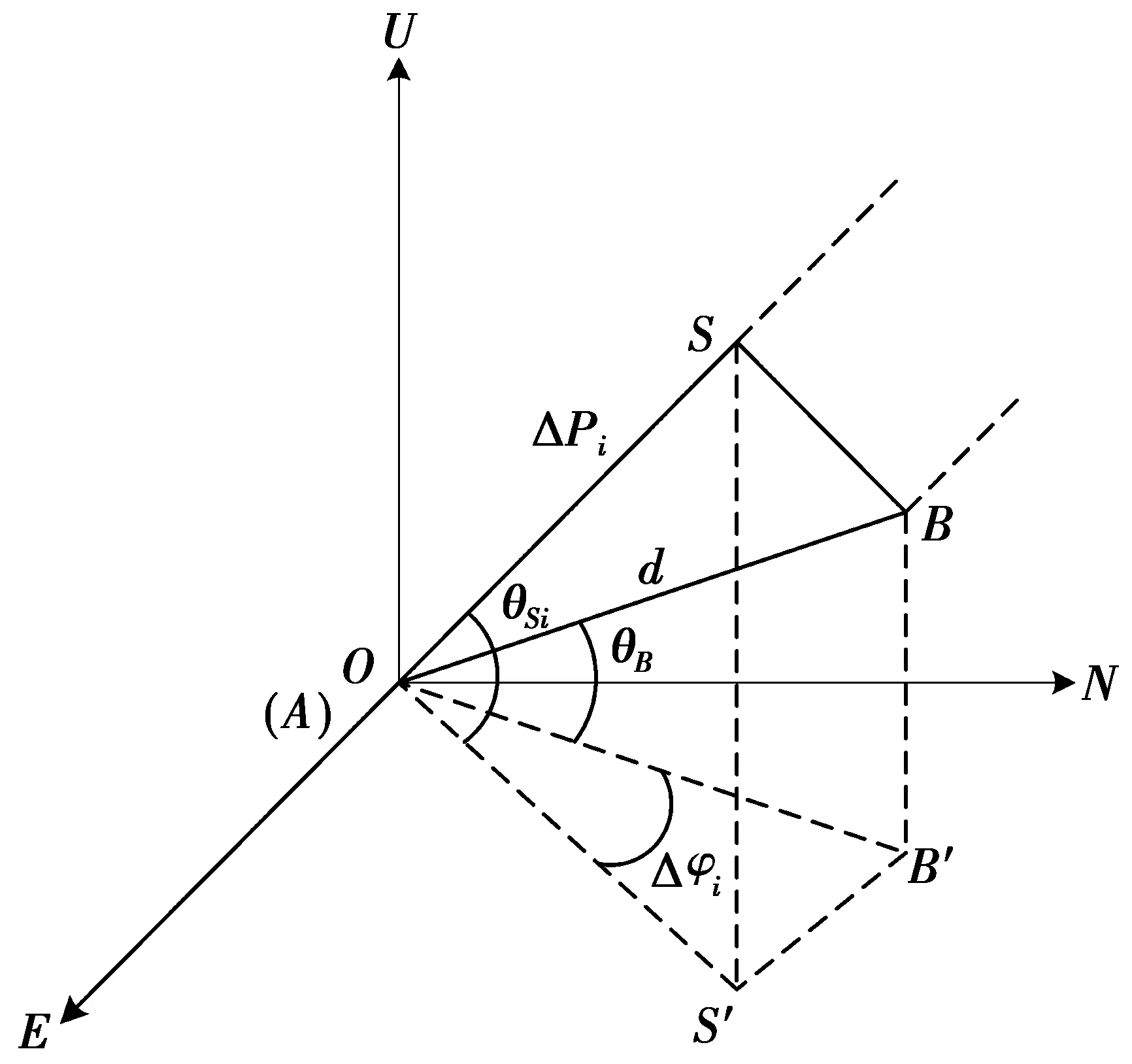
图1　基线AB在ENU坐标系示意图Fig.1　Baseline AB in the ENU coordinate system

设ΔPi为A，B到卫星距离的差值，Li为A，B对卫星i的单差载波相位观测值，Ni为单差整周模糊度，则有[7]

(3)

进一步做双差，可得

(4)

(4)式中：ΔLij为双差载波相位观测值；ΔNij为双差整周模糊度；θSj为卫星j的仰角；Δφj为卫星j与基线的航向角之差。

2.2基本模糊度组搜索范围确定

从所有双差模糊度中选取2个作为基本模糊度组，选取方法见2.4节推导。首先利用伪距精度对搜索范围进行约束。考虑观测噪声的影响，伪距和载波相位双差方程可表示为

(5)

(5)式中：Δρij为双差伪距；ερij为双差伪距噪声；εΔLij为双差载波相位噪声。

由于载波相位观测噪声远小于伪距观测噪声，两式相减可忽略εΔLij的影响[8]，得

(6)

(7)

进一步利用基线约束条件限制模糊度搜索范围，将双差方程移项整理得

(8)

(9)

综合(7)式和(9)式，可确定模糊度搜索范围为

(10)

由于整周模糊度为整数，所以根据 (10) 式可确定出双差模糊度的整数取值范围。

2.3剩余模糊度组合确定

选取卫星k为参考卫星，与卫星i和卫星j共同作为基本卫星组，根据(3)式，可得双差方程组为

(11)

记eik，ejk的俯仰角、航向角分别为θik，φik和θjk，φjk，有

(12)

(13)

记g=φik-φB，f=φjk-φik，则可解得基线俯仰角θB和航向角φB分别为

(14)

由于解算过程中的三角函数变换导致了多值问题，每一组整周模糊度对应12组俯仰角和航向角解。为了检验解的正确性，根据俯仰角和航向角的实际取值范围(分别为-90°～90°，0°～360°)剔除误解，再将剩余解代回方程组(12)进行检验。多次实验结果表明，每一组整周模糊度对应0～2组俯仰角和航向角的解。

对所有俯仰角和航向角组合进行搜索，由(4)式可知，每一组角度值都可以解算出一组整周模糊度浮点解，为

(15)

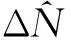
(16)

可以看出，新方法以俯仰角和航向角作为中间变量，只需2个基本模糊度就完成了所有待搜索模糊度的解算，有效减小了搜索空间。

2.4基本卫星组选取

俯仰角和航向角的解算精度与基本卫星组的选取有关，合理的卫星选取能够解得更加精确的角度组合，从而保证剩余模糊度的正确解算[10]。由算法具体过程可知，载波相位观测噪声会对u和v产生影响，进而影响俯仰角和航向角的解算精度。分别求u对ΔLik，v对ΔLjk的偏导数为

(17)

由于仰角最大的卫星信号条件较好，一般选取其作为参考卫星k，并作为基本卫星之一。另外2颗基本卫星i和j的选取原则是使(17)式中偏导数绝对值尽可能小，从而可以减小噪声对解算精度的影响。由θik和θjk定义，卫星i，j的俯仰角越小，sinθik和sinθjk的值越大，但仰角过低又会影响信号质量，综合考虑，论文取仰角为45°附近的2颗卫星，同时还应使卫星i和j的航向角与参考卫星k的差值尽量大从而使|si-sk|和|sj-sk|的值尽量大。

2.5整周模糊度固定

L=Ax(t)+BN

(18)

(18)式中：L为双差载波相位观测值；A，B为系数矩阵；N为整周模糊度值；x(t)为基线矢量。由最小二乘解算得到基线矢量，并与实际长度相比得基线残差为

(19)

理论上，当搜索到正确模糊度组时，所解算出的基线残差最小。然而由于观测噪声等因素的影响，在短时间内，并不能保证正确模糊度组所对应的基线残差与其他搜索组合所对应的残差有明显不同。但是正确的模糊度组合所解得的基线残差在多个历元内应始终保持较小，因此可利用多个历元下的观测数据，在基线残差之和最小的情况下完成整周模糊度的固定。设历元个数为m，分别找出基线二次残差之和的次小值与最小值，令：

(20)

当满足(20)式时，将xi(t)所对应的模糊度组作为最终固定解。算法流程如图2所示。

图2　改进型最小二乘搜索流程图Fig.2　Flow chart of improved least squares search

3实验分析

3.1实验条件

将2个型号为GPS-703-GGG的GNSS天线分别固定在基线两端，并放置在小车上。利用2个NovAtel OEM628板卡和一个SPAN-CPT型号的组合系统(提供姿态信息，其Y轴方向与基线方向一致)进行数据采集，实验地点为学院操场，采样频率为1 Hz，卫星截止角设为10°。第1组实验，记为Ⅰ，基线长度为1.907 m，俯仰角和航向角分别为0.10°和229.15°，可视卫星共8颗，PRN(pseudo random noise)分别为1，14，16，20，25，29，31，32，其中PRN31仰角最大，取其为参考卫星，首先进行400 s静态数据采集，然后绕操场行驶进行动态数据采集。第2组实验，记为Ⅱ，基线长度为3.49 m，俯仰角和航向角分别为7.76°和9.30°，可视卫星共6颗，PRN分别为2，4，10，17，20，28，取仰角最大的PRN4为参考卫星。

3.2静态实验及结果分析

根据论文选星原则，第1组实验选取PRN31，PRN14和PRN32为基本卫星组，第2组实验选取PRN4，PRN17和PRN10为基本卫星组。首先根据(10)式确定出基本模糊度组的搜索范围分别为Ⅰ：[8 388 602,83 88 619]和 [8 388 607,8 388 621]；Ⅱ：[99 713,99 740]和[-91311,-91 273]，再利用俯仰角和航向角的范围及方程组(12)的约束剔除误解，最终分别得到340组和1 592组的待检测模糊度。根据文献[6],采用普通最小二乘搜索算法时，模糊度搜索范围为±2int(基线长度/λ+0.5),所以在基线长度为1.907 m和3.49 m情况下分别需要搜索433=79 507次和713=357 911次。可以看出新方法所需搜索次数明显少于普通最小二乘搜索。然后根据确定的搜索空间，利用文中算法进行整周模糊度的固定，并与传统最小二乘搜索算法进行对比，结果如表1所示。

由于固定整周模糊度时对浮点解进行了取整，所以不同的角度值可能对应相同的模糊度值，也就是说只要搜索的俯仰角和航向角组合与真实值差距很小，就可以保证该角度组合能够解得正确的模糊度组合。2次实验中最终确定的角度组合分别为(0.883 5°，229.327 9°)和(7.063 3°，9.573 5°)，与真实值(0.10°，229.15°)和(7.76°，9.30°)基本相当，从另一方面也证明了该算法的正确性。

表1　整周模糊度解算结果

在模糊度的确认过程中，基线残差次小值与最小值往往需要较长的时间才能满足比值要求，而新方法利用基线及其与俯仰角、航向角的约束关系，不仅有效减少了待搜索模糊度组合的个数，而且降低了出现与最佳角度组合相近值的可能性，从而有利于模糊度的确认，缩短了初始化时间。两组实验所需初始化时间分别为39 s和43 s，而采用普通最小二乘搜索均需要100 s以上。

根据姿态解算方法，分别计算出基线的长度、俯仰角和航向角，得到其误差曲线如图3和图4所示，均方根误差(root mean square error,RMSE)如表2所示。

图3　基线长度1.907 m时结果误差曲线Fig.3　Error curve with 1.907 m baseline

图4　基线长度3.49 m时结果误差曲线Fig.4　Error curve with 3.49 m baseline

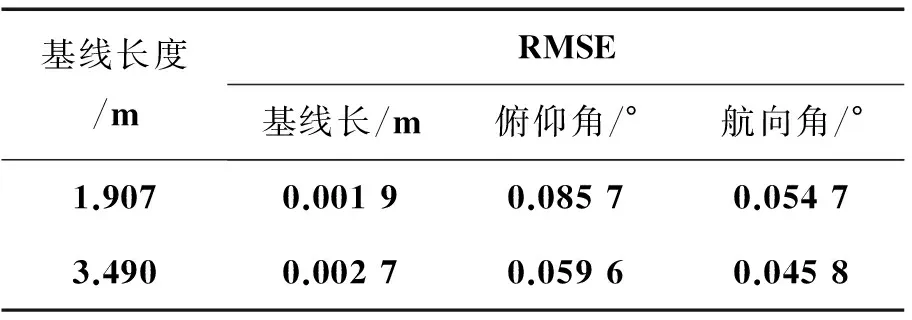
基线长度/mRMSE基线长/m俯仰角/°航向角/°1.9070.00190.08570.05473.4900.00270.05960.0458

可以看出，采用本文方法，在基线长度分别为1.907 m和3.490 m时，只需在较短时间内分别搜索340次和1 952次即能正确固定整周模糊度，进而得到精度较高的姿态信息，基线长度均方根误差在1 cm内，俯仰角和航向角的RMSE均在0.1°内。

3.3动态实验及结果分析

在第1组静态实验的基础上进一步进行动态实验，小车在操场内做近似圆周运动，基线俯仰角变化较小，航向角在0°～360°变化。利用同样的方法进行动态姿态解算，得到基线长度误差、俯仰角误差和航向角误差曲线如图5所示。

由于动态情况下基线的俯仰、航向信息基准较难获取[11]，本文利用SPAN-CPT型号GPS/INS组合系统提供的姿态角作为基准，但其本身也存在较大的误差(水平姿态误差0.1°，航向误差0.2°)，进而会影响姿态测量精度的验证，这也是图5出现较大误差的主要原因，但整体上看，动态条件下基线长度均方根误差为0.39 cm，基线航向角和俯仰角误差分别在0.5°和0.7°以内，可以体现出姿态测量的有效性。

图5　动态实验结果误差曲线Fig.5　Error curve of dynamic experiment

4结束语

理论分析及实验结果表明：

1)本文所提基于改进型最小二乘搜索的GNSS姿态测量方法充分利用了基线长度与俯仰角、航向角之间的关系，将基本模糊度组中的模糊度个数由3个减少为2个，不仅缩小了搜索范围，提高了搜索效率，同时减弱了其他模糊度搜索组合对最佳组合的影响，缩短了初始化时间。

2)利用伪距和基线约束条件进一步限制了基本模糊度组的取值范围，并对基本卫星组的选取进行了分析，静态和动态实验均取得了较好效果。

参考文献：

[1]刘经南,邓辰龙,唐卫明.GNSS整周模糊度确认理论方法研究进展[J].武汉大学学报,2014,39(9):1009-1016.

LIU Jingnan,Deng Chenlong,Tang Weiming. Review of GNSS Ambiguity Validation Theory[J].Geomatics and Information Science of Wuhan University,2014,39(9):1009-1016.

[2]PURIVIGRAIPONG S, HODGART S, UNWIN M, et al. Resolving Integer Ambiguity of GPS Carrier Phase Difference[C]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 832-847.

[3]刘志俭,胡小平,贺汉根.GPS姿态传感器的数学原理和实现[J].传感技术学报,2003,16(2):199-202.

LIU Zhijian,HU Xiaoping,HE Han’gen.The Mathematics Theory and Realization of GPS Attitude Sensor[J].Journal of Sensors and Actuators,2003,16(2):199-202.

[4]王立红, 郝继平, 汤云. 基于最小二乘法的GPS多天线测姿及精度分析[J]. 测试技术学报, 2007, 21(1): 1-5.

WANG Lihong, HAO Jiping, TANG Yun. Attitude Determination and Accuracy Analysis by Multi-antenna GPS Technology Based on Least Square Algorithm[J]. Journal of Test and Measurement Technology,2007,21(1):1-5.

[5]庞春雷, 赵修斌, 卢艳娥，等. 短基线约束条件下整周模糊度二维搜索算法[J]. 中国空间科学技术, 2012, (3): 43-48.

PANG Chunlei, ZHAO Xiubin, LU Yan’e, et al. Planar Search Algorithm for GPS Ambiguity Resolution with Short Baseline Length Constraint[J]. Chinese Space Science and Technology, 2012, (3): 43-48.

[6]任光辉, 茅旭初. 多约束条件的全球定位系统单频单历元短基线定向技术与实现[J]. 上海交通大学学报, 2014, 48(3): 335-340.

REN Guanghui, MAO Xuchu. Single Frequency and Single Epoch Short-Baseline GPS Orientation Determination Method and Realization with Multiple Constraints[J]. Journal of Shanghai Jiaotong University. 2014, 48(3): 335-340.

[7]庞春雷, 赵修斌, 余永林，等. 低精度SINS初始对准/GPS双天线测向互辅算法研究[J]. 西安电子科技大学学报(自然科学版), 2014, 41(6)：167-173.

PANG Chunlei, ZHAO Xiubin, YU Yonglin, et al. Interact Arithmetic of Low-Accuracy SINS’ Initial Alignment and GPS Orientation Measurement with Two Antennas[J]. Journal of Xidian University (Natural Science), 2014, 41(6)：167-173.

[8]WANG Bo, MIAO Lingjuan, WANG Shunting, et al. A constrained LAMBDA method for GPS attitude determination[J].GPS solutions, 2009(13): 97-107.

[9]JIN Wenrui, ZHAN Xingqun. Hybrid analytical resolution approach based on ambiguity function for attitude determination[J]. Journal of Zhejiang University. 2009, 10(7): 1038-1048.

[10] 陈万通, 秦红磊, 丛丽，等. 基于球面交点的AFM算法的误差分析与改进方法[J]. 电子与信息学报, 2010, 32(9): 2220-2225.

CHEN Wantong, QIN Honglei, CONG Li, et al. Error Analysis and Improvement of The Ambiguity Function Method Based on The Intersection Point on Sphere[J]. Journal Electronics and Information Technology. 2010, 32(9): 2220-2225.

[11] 王勇, 赵修斌, 庞春雷，等. 一种载波相位动态相对定位精度验证方法[J].测控技术,2015,34(3):36-39.

WANG Yong, ZHAO Xiubin, PANG Chunlei. An Authentication Method of Dynamic Relative Positioning Using Carrier Phase[J]. Measurement and Control Technology, 2015, 34(3): 36-39.

Method based on improved least squares search for GNSS attitude measurement

LI Shijie, LI Zhian, PANG Chunlei, LIU Ming

(Information and Navigation College, Air Force Engineering University, Xi’an 710077, P.R.China)

Abstract:Based on the feature that the baseline is known in the attitude measurement of Global Navigation Satellite System (GNSS), an improved least squares search method is proposed in the following procedures: First, the integer ambiguity group is divided into basic group and remaining group. Given the pseudo range accuracy and baseline length, the search space for basic group is deduced. Then the remaining group could be constructed from the basic group, based on the relations between ambiguity and baseline heading and elevation. In this process, the heading and elevation was regarded as the intermediate variable. Finally, the baseline vector is calculated by least squares method. By comparing two-order residuals of baseline, integer ambiguity can be defined and therefore the attitude measurement is completed. The experiment result reveals that this improved method can effectively reduce the size of search space and the initialization time. The method is with a relatively high precision, meeting the demand for GNSS attitude measurement.

Keywords：global navigation satellite system; least squares search; integer ambiguity; attitude measurement; baseline constrain

DOI：10.3979/j.issn.1673-825X.2016.02.008

收稿日期：2015-03-25

修订日期：2015-12-30通讯作者：李世杰lishijiepaper@163.com

基金项目：国家自然科学基金资助项目(61273049)

Foundation Item：The National Natural Science Foundation of China(61273049)

中图分类号：TN967.1

文献标志码：A

文章编号：1673-825X(2016)02-0187-07

作者简介：

李世杰(1990-),男，河南安阳人，硕士研究生，主要研究方向为卫星导航与定位。E-mail:lishijiepaper@163.com

(编辑：魏琴芳)