基于Fr-AF与改进RIDT的QFM-PRBC伪码估计

张天骐，廖　畅，叶　飞，欧旭东

(重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)



基于Fr-AF与改进RIDT的QFM-PRBC伪码估计

张天骐，廖畅，叶飞，欧旭东

(重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)

摘要：针对二次调频-伪码调相 (quadratic frequency modulated-pseudo random binary phase code，QFM-PRBC) 复合信号伪码估计的难题，提出一种基于分数阶模糊函数(fractional ambiguity function，Fr-AF)和改进的三角窗抗干扰核函数(reduced interference distribution kernel based on the triangular window，RIDT)变换的伪码估计算法。应用平方法解决伪码与信息码相位突变问题，并用累加平均减小平方法带来的噪声影响，利用分数阶模糊函数估计平方累加后信号的最高项和次高项系数，重构信号对接收端信号降阶；采用奇异值分解(singular value decomposition，SVD)对基于三角窗减少干扰的核函数变换加以改进以提取降阶后信号的伪码序列。仿真实验表明了算法的有效性，当累加次数为20且信噪比在-4 dB以上时，伪码可以正确估计。

关键词：二次调频-伪码调相；分数阶模糊函数；改进的三角窗抗干扰核函数(RIDT)；伪码估计

0引言

伪码调相和载波调频复合信号是雷达引信系统中采用的更为复杂的调制信号，它结合2种信号的优势，具有良好的测速测距精度、截获概率低、抗干扰性能好等特点，因此，在雷达和微小探测器中应用广泛。因为伪码调相和载波调频信号中特征参数多，载波调制复杂，为该类信号的参数估计带来了巨大的挑战，所以，如何有效地提取该类信号的特征对于电子对抗等应用具有重要意义。

二次调频-伪码调相 (quadratic frequency modulated-pseudo random binary phase code，QFM-PRBC) 信号是一种脉内二次调频、脉间调相的复合信号。目前国内针对线性调频-伪码调相复合信号、正弦调频-伪码调相复合信号的特征研究较多，而关于二次调频-伪码调相复合信号的特征参数提取的文献并不多见，特别地，研究其伪码序列的文献更是少有。何丹娜[1-2]等基于三次相位函数和频谱搬移对二次调频-伪码调相信号的伪码进行了研究，而频谱搬移的抗噪性能、准确率有待于进一步的提升。因此，新方法亟待补充应用于该复合信号的特征提取，在更低信噪比下，实现伪码的正确估计。

虽然QFM-PRBC信号可以近似看为低信噪比下的高动态直扩信号，但同直扩信号相比，其载波调制过于复杂，适用于直扩信号的伪码估计方法[3]不能适用于该信号。而在通信中，这类复合信号的伪码估计具有重要的意义，如信号的捕获和跟踪，实现有效干扰等。因而本文研究的是如何有效地获得QFM-PRBC信号的伪码信息。

1信号模型

带有信息码的QFM-PRBC信号的数学表达式为[1-2]

(1)

2QFM-PRBC伪码估计的算法原理

(2)

(2)式中：w(nTs)是采样后噪声；s(nTs)是QFM-PRBC信号的离散形式，表示为

(3)

(4)

(4)式中，L为接收到的信号长度。

为了估计QFM-PRBC信号的伪码，先要消除载波调制中高动态部分的影响。为了消除高动态部分的影响，可以先估计出次高项的系数a22和最高项系数a33，然后重构信号对复合信号降阶。但是QFM-PRBC信号其信息码及伪码符号对a22，a33估计会带来影响。这里利用平方法解决信息码及伪码符号的影响，并用累加平均法消减平方法带来的噪声影响。QFM-PRBC信号伪码估计的流程图如图1所示。

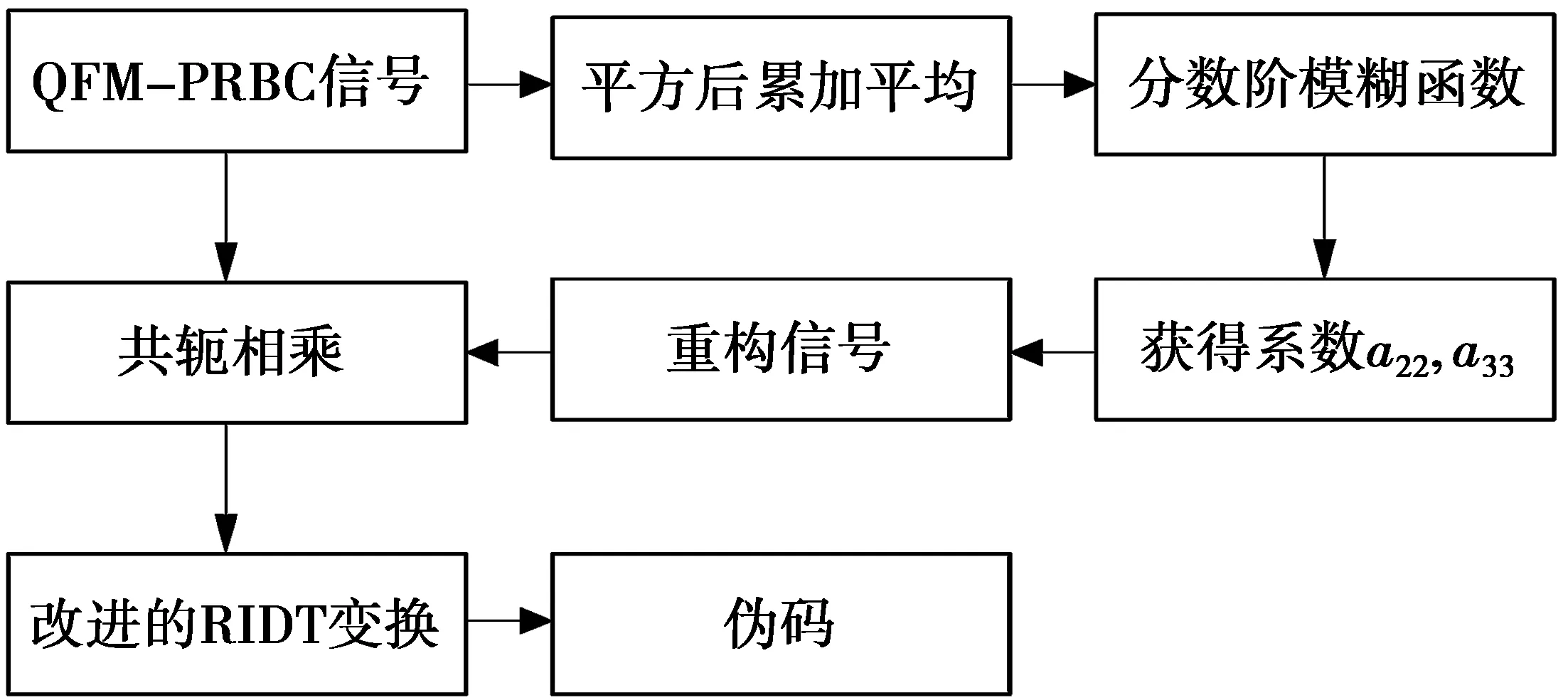
图1　二次调频-伪码调相复合信号伪码估计的流程图Fig.1　Procedure of estimation for PN Code of the QFM-PRBC

首先利用平方法消去QFM-PRBC信号的信息码及伪码符号的影响，表示为

(5)

代入(3)式可得

(6)

所以 (5)式可简化为

(7)

(7)式中：s1(n)=s2(n)是平方后二次调频信号，它的系数是原信号系数的2倍；w1(n)=2s(n)w(n)+w(n)为平方后产生的新噪声。

累加平均后，对带噪二次调频信号中的二、三阶系数进行估计。这里采用分数阶模糊函数(fractionalFouriertransforms,FRFT)[5-6]对其进行估计，具体理论分析如下。

分数阶傅里叶变换的核函数为

Kp(t,u)=

(8)

分数阶傅里叶变换的模糊函数定义为

(9)

对二次调频信号x(t)=ej(a0+a1t+a2t2+a3t3),代入(9)式，则其分数阶傅里叶变换的模糊函数为

(10)

整理可得到

(11)

为方便后面的理论推导，引入(12)式

(12)

1)当α=2nπ时，

(13)

2)当α=(2n+1)π时，

(14)

3)当α≠nπ且cotα=-6a3τ时，

(15)

4)当α≠nπ且cotα≠-6a3τ时，

(16)

但是在参数估计过程中搜索角度α的同时，还需要对(u,τ)平面进行搜索，这将为估计a2，a3带来巨大的计算量。而根据参考文献[5]可知，为获得最优的a2估计，延时参数τ取0.2×2N；为获得最优的a3，延时参数τ取0.14×2N，其中2N为取样数据长度。

(17)

(18)

(18)式中，z(n)含有的伪码与y(n)中伪码信息是一样的，所以，下一步对z(n)的伪码进行估计即可得到QFM-PRBC的伪码。

根据文献[7]，伪码调相复合信号经伪维格纳分布(pseudoWigner-Villedistribution，PWVD)变换后，相位突变点信息在最高幅度输出上转换为一系列的三角脉冲，且三角脉冲的幅度大小与分析窗长成正比。设g为窗长，其定义式为

(19)

(19)式中：Rs(t,τ)=s(t+τ/2)s*(t-τ/2)表示s(t)瞬时自相关函数。但是，经PWVD变换后，噪声的干扰、交叉项的干扰将会影响伪码的估计。

为了减小交叉项的干扰，采用JechangJeong和WilliamJWilliams[8]提出的基于三角窗抑制干扰的核函数，其变换定义为

(20)

而为了抑制噪声的影响，本文引入奇异值分解消除部分噪声干扰。令S=RIDTs(t,ω)，表示降阶后的复合信号经三角窗抗干扰核函数(reduced interference distribution kernel based on the triangular window，RIDT)变换后的时频面，对它进行奇异值分解，即S=UΛVH。其中，H表示共轭转置，U，V均为正交阵，Λ为非负对角矩阵。保留Λ中最大的特征值，令其他特征值为0，得到新的矩阵Λ1，由此可得不含噪声的时频面S1=UΛ1VH。如此，可以对PWVD变换后的时频面S′=PWVDs(t,ω)进行奇异值分解(singular value decomposition，SVD)分解，相同处理后得到不含噪声的时频平面S2。

综上所述，QFM-PRBC信号伪码估计的步骤如下。

步骤1通过平方法消除信号y(n)中信息码和伪码的影响，并通过累加平均法降低平方法带来的噪声影响。

步骤3对信号z(n)进行RIDT变换，并通过SVD得到不含噪的时频平面S1，提取S1中最小切平面，通过切平面中三角脉冲的特征获得伪码的估计。

3仿真实验及其分析

从理论上分析了算法的可行性后进行实验仿真验证。设接收信号为采样后的信号。采样频率为fs=510MHz，伪码位数Q=15。

仿真图2是不同信噪比条件下，不同累加次数对参数估计正确率的影响图。由图2可知，随着信噪比的增大，检测的正确率随之增大直至最佳。同一信噪比下，检测正确率未达到最佳，累加次数越大，检测的正确率越大，即增加累加次数可以改善参数估计的性能。而且在信噪比≥-4dB，J=20时，高阶系数的估计值都稳定在误差允许的范围内且计算量较低，这有利于后面的伪码序列估计。

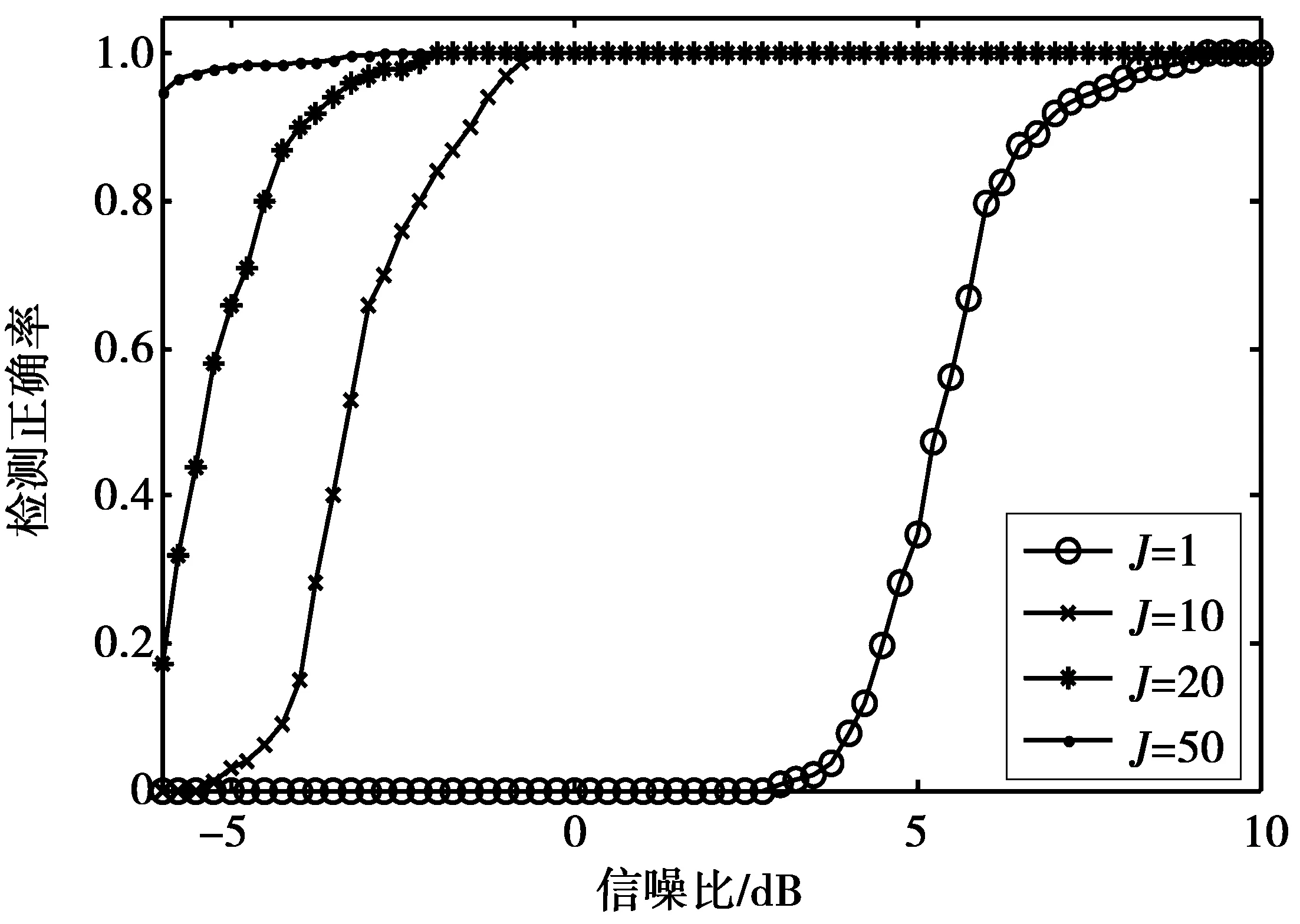
图2　不同累加次数、不同信噪比时系数估计正确率图Fig.2　Estimation accuracy of coefficients under different SNRand different cumulative frequency

实验二信号伪码序列估计。考虑到实验一中的估计误差，在信噪比为-4dB的情况下，分别使用改进的PWVD变换、未改进的RIDT变换、改进的RIDT变换对复合信号的伪码进行估计。

仿真结果如下，图3是伪码波形；图4是经改进的PWVD变换的三维图及对应提取的切平面；图5是经RIDT变换的三维图及对应提取的切平面；图6是经改进的RIDT变换的三维图及对应提取的切平面。

图3　伪码序列Fig.3　Pseudo-code sequences

图4　经改进PWVD三维图及其对应提取切平面Fig.4　Three-dimensional figure through MPWVD and corresponding extracted minimum tangent plane

同一信噪比下，图4b中改进PWVD提取的切平面相对RIDT直接提取的切平面相对清晰，但是干扰峰较多，不能准确提取。图5b中RIDT直接提取的切平面淹没在噪声中，所需信息不能分辨。图6b中经改进的RIDT变换提取的切面图相对于前面方法提取的切面图清晰明了，这更有利于正确的提取伪码信息。由此通过改进RIDT变换后，根据三角脉冲特征可以获得伪码估计为[1 1 1 -1 1 1 -1 -1 1 -1 -1 -1 -1 1 1] 或[-1 -1 -1 1 -1 -1 1 1 -1 1 1 1 1 -1 -1]，和图3中伪码序列对比可知，伪码估计是正确的。

图5　经RIDT三维图及其对应提取切平面Fig.5　Three-dimensional figure through RIDT and corresponding extracted minimum tangent plane

图6　改进RIDT三维图及其对应提取切平面Fig.6　Three-dimensional figure through MRIDT and the corresponding extracted minimum tangent plane

4结束语

本文针对QFM-PRBC信号的伪码估计问题进行了研究，提出了一种基于分数阶模糊函数和奇异值分解改进RIDT变换的伪码盲估计算法。在应用平方法解决伪码与信息码的相位突变的问题之后，通过累加平均降低的交叉项噪声、噪声的影响。然后利用分数阶模糊函数对信号系数估计，再重构信号对接收端复合信号降阶。最后采用利用奇异值分解改进的基于三角窗抑制干扰的核函数变换提取伪码序列。理论分析和仿真实践证明了该算法具有可行性和有效性，在信噪比为-6dB，累加次数为50时，可以较为准确地估计参数。当信噪比≥-4dB，累加次数为20时，可以正确完成伪码估计。这对该类信号的捕获与跟踪、实现有效干扰等应用具有一定参考价值。

参考文献：

[1]何丹娜, 张天骐, 高春霞，等. 线性调频—伪码调相复合信号的伪码盲估计新算法[J]. 电讯技术, 2012, 52(6): 906-912.

HEDanna,ZHANGTianqi,GAOChunxia，etal.NewblindestimationalgorithmforPNCodeofReconnaissanceSignalCombinedPRBCandLFM[J].TelecommunicationTechnology2012, 52(6): 906-912.

[2]何丹娜, 张天骐, 高丽，等. 二次调频—伪码调相复合信号的伪码盲估计[J]. 电子技术应用, 2013, 39(5): 100-103.

HEDanna,ZHANGTianqi,GAOLi，etal.BlindEstimationforPNCodeofReconnaissanceSignalCombinedwithQuadraticFrequencyModulatedandPseudo-RandomBinaryPhaseCode[J].ApplicationofElectronicTechnology, 2013, 39(5): 100-103.

[3]张天骐，张传武，林孝康，等. 直扩信号伪码周期及序列的估计算法[J].系统工程与电子技术2005,27(8): 1365-1368.

ZHANGTianqi,ZHANGChuanwu,LINXiaokang，etal.AlgorithmsforperiodandsequenceestimationofthePNcodeinDS-SSsignals[J].EngineeringandElectronics, 2005,27(8): 1365-1368.

[4]贺成艳, 卢晓春. 用于GNSS基带信号分析的相干累加算法[J].数据采集与处理, 2009,24(Z1):124-127.

HEChengyan,LUXiaochun.NewCoherentAccumulationAlgorithmforFurtherPropertyAnalysisofGNSSBasebandSignals[J].JournalofDataAcquisition&Processing, 2009, 24(Z1): 124-127.

[5]曲强. 多项式相位信号与循环平稳信号处理算法研究[D]. 大连：大连理工大学, 2010.

QUQiang.StudyonAlgorithmsofPolynomialPhaseSignalandCyclostationarySignalProcessing[D].Dalian：DalianUniversityofTechnology, 2010.

[6]郭海燕, 董云龙, 关键. 基于分数阶模糊函数的海面运动弱目标检测[J]. 系统工程与电子技术,2011,33(6):1212-1216.

GUOHaiyan,DONGYunlong,GUANjian.Weaktargetdetectioninseaclutterbasedonfractionalambiguityfunction[J].SystemsEngineeringandElectronics, 2011, 33(6):1212-1216.

[7]李明孜, 赵惠昌. 基于PWD变换的伪码调相-载波调频复合信号的特征提取技术研究[J]. 兵工学报, 2007, 28(7): 808-811.

LINGMingzi,ZHAOHuichang.StudyonFeaturesExtractionofPseudoCodePM-CarrierFMCombinedSignalBasedonthePWDTransform[J].ACTAARMAMENTARII, 2007, 28(7): 808-811.

[8]JEONGJechang,WILLIAMSWJ.Kerneldesignforreducedinterferencedistributions[J].SignalProcessing,IEEETransactionson, 1992, 40(2) :402-412.

Estimation for PN code of reconnaissance signal combined with QFM-PRBC based on Fr-AF and modified RIDT

ZHANG Tianqi, LIAO Chang, YE Fei, OU Xudong

(Chongqing Key Laboratory of Signal and Information Processing, Chongqing University of Posts and Telecommunications,Chongqing 400065, P.R.China)

Abstract:To estimate the pseudo noise (PN) code of reconnaissance signal combined by the quadratic frequency modulated (QFM) and pseudo-random binary phase code (PRBC), the paper presents an algorithm based on the fractional ambiguity function and a modified time-frequency analysis method using a reduced interference distribution (RID) kernel based on the triangular window. Firstly, the square method is computed to eliminate the phase mutation, and the accumulated method is used to reduce the bad effect of the square method. Secondly, fractional ambiguity is adopted to estimate second and third coefficients. Then the original signal is multiplied by the conjugated signal which is reconstructed by the estimated coefficients to get a new compound signal. Thirdly, the new compound signal consists of sine carrier and the PRBC signal, and the original PN code can be restored by the way of RIDT which is modified by the singular value decomposition (SVD). The simulation results show that the algorithm is feasible. The correct PN code is obtained when signal-to-noise ratio is more than or equal to -4 dB, which shows good performance.

Keywords：quadratic frequency modulated-pseudo random binary phase code(QFM-PRBC); fractional ambiguity; reduced interference distribution kernel based on the triangular window(RIDT)；estimation of pseudo noise(PN) code

DOI：10.3979/j.issn.1673-825X.2016.02.003

收稿日期：2015-05-07

修订日期：2015-12-14通讯作者：廖畅672388299@qq.com

基金项目：国家自然科学基金(61371164,61275099,61102031)；信号与信息处理重庆市市级重点实验室建设项目(CSTC2009CA2003)；重庆市杰出青年基金(CSTC2011jjj140002)；重庆市自然科学基金(CSTC2012JJA40008)；重庆市教育委员会科研项目(KJ120525，KJ130524)；重庆市研究生科研创新项目(CYS14140)

Foundation Items：The National Natural Science Foundation of China (61371164, 61275099, 61102131)；The Project of Key Laboratory of Signal and Information Processing of Chongqing (CSTC2009CA2003)；The Chongqing Distinguished Youth Foundation (CSTC2011jjjq40002)；The Natural Science Foundation of Chongqing (CSTC2012JJA40008)；The Research Project of Chongqing Educational Commission (KJ120525, KJ130524)；The Graduate Research and Innovation Projects of Chongqing (CYS14140)

中图分类号：TN911.7

文献标志码：A

文章编号：1673-825X(2016)02-0156-06

作者简介：

张天骐(1971-)，男，四川眉山人，教授，博士生导师，主要研究方向为宽带微弱无线电信号处理、盲信号与信息处理、语音信号处理等。E-mail:zhangtq@cqupt.edu.cn。

廖畅(1990-)，男，湖北荆州人，硕士研究生，主要研究方向为复杂信号处理。E-mail: 672388299@qq.com。

叶飞(1992-)，女，安徽安庆人，硕士研究生，主要研究方向为单通道盲源分离。

欧旭东(1990-)，男，湖南岳阳人，硕士研究生，主要研究方向为语音信号卷积盲源分离。

(编辑：王敏琦)