气液两相流段塞流持气率快关阀法优化设计

赵安，韩云峰，张宏鑫，刘伟信，金宁德（天津大学电气与自动化工程学院，天津 300072）



气液两相流段塞流持气率快关阀法优化设计

赵安，韩云峰，张宏鑫，刘伟信，金宁德
（天津大学电气与自动化工程学院，天津 300072）

摘要：快关阀法（quick closing valve，QCV）是气液两相流流动实验中常用持气率标定手段。特别是由于段塞流中气塞与液塞表现为随机可变流动特性，不合理的快关阀间距及截取次数选择将会导致持气率测量误差增大。提出了一种持气率快关阀法优化设计方案。首先，采用环形电导传感器上下游阵列信号计算流体相关流速，根据相关测速结果提取上游传感器信号对应流动工况的气塞与液塞间隔长度序列，采用Maxwell方程提取液塞中含泡持气率；在此基础上，再依气塞在管道内占比模拟计算不同快关阀间距时捕获的持气率波动序列。通过分析持气率序列波动，从统计学角度指出了95%置信度及5%允许误差情况下所需最低截取次数。最后，在快关阀门间距为1.55 m的条件下对段塞流所需截取次数进行了实验验证。通过对快关阀法持气率测量误差进行统计分析，证明了设置两个快关阀门间距的充分条件。

关键词：气液两相流；段塞流；持气率；快关阀法

2015-08-12收到初稿，2015-10-09收到修改稿。

联系人：金宁德。第一作者：赵安（1990—），男，博士研究生。

Received date: 2015-08-12.

Foundation item: supported by the National Natural Science Foundation of China (51527805，11572220) and the National Science and Technology Major Project (2011ZX05020-006).

引　言

段塞流经常发生在热能及水动力气液两相流系统中。其中，持气率是描述两相流流动行为、建立流动模型及预测质量、动量及能量传递的重要参数。由于段塞流中气塞及液塞流动结构沿管道轴向方向随机多变，段塞流持气率难以测量，故在气液两相流实验系统中提供可靠的段塞流标定手段具有重要学术价值及实际意义。

通常采用电学法、声学法、光学法等测量持气率。电学法具有响应速度快及易于测量等特点，通过测量混合流体电学性质变化（电导和电容），被广泛应用于两相流持气率参数检测[1-11]。由于气相与水相之间显著的密度差异特性，采用声学法和光学法可取得较好的持气率测量效果[12-14]。为了评价持气率测量特性，通常需在两相流实验装置上设计持气率标定系统。快关阀（QCV）法因其操作简便已广泛作为气液两相流实验装置上的持气率标定手段[15-17]。快关阀法持气率测量是通过快速截取两阀门间的气液两相流，待气相及液相因重力分离后测出相应体积，进而换算得到持气率。为保证持气率测量精度，实验时需对每种流动工况多次重复测量。实验表明，气液两相流流动结构及快关阀门间距是影响QCV法持气率测量精度的主要因素。对于尺度较小的流动结构（如泡状流、混状流及环状流），较短的快关阀门间距及较少的快关阀截取次数即可获得满意的持气率测量精度；但是，对于尺度较大的段塞流，由于气塞及液塞流动结构沿管道轴向方向随机多变，不合理的快关阀门间距及截取次数选择会导致较大的持气率测量误差。

快关阀法是目前气液两相流实验系统中常规的持气率标定手段，但是，尚未见文献中对快关阀间距及截取次数优化设计的报道。为此，本文首先在垂直上升气液两相流20 mm管径中采用环形电导传感器阵列测取段塞流中气塞及液塞长度序列，然后，由Maxwell方程分别计算得到段塞流中含泡液塞及气塞的持气率，进而模拟计算得到段塞流流动结构的持气率波动序列，最后从统计学角度分析指出95%置信度及5%允许误差情况下所需最低快关阀截取次数及设置快关阀间距的充分条件。

图1　垂直上升气液两相流实验装置Fig.1　Experimental facility for vertical upward gas-liquid two-phase flow

1　实验装置

垂直上升管中气液两相流实验装置如图1所示。实验中水相从管道最下方通入，其流量计量采用工业级蠕动泵（WT300F）。实验气体是由空气压缩机产生，并从管道下端侧部进入。为防止流体回流进入气路管道，在管道下端侧部气相出口处安装有止回阀。实验测试段采用内径为20 mm的有机玻璃管。实验时，气相表观流速范围为0.055～0.479m·s-1，液相表观流速范围为0.037～0.884 m·s-1。实验共配比了63组气液两相流流动工况，在垂直上升管段中观察到的实验流型有段塞流（slug）、混状流（churn）和泡状流（bubble），关于流型描述见文献[18]。

实验中，首先固定气相表观速度，逐渐增加水相表观速度，依次循环完成。待每个气液两相流流动工况配比稳定后，再进行测试段的环形电导传感器信号测量，选用NI公司PXI 4472数据采集卡，并结合图形化编程语言 LABVIEW 7.1实现数据实时采集、存储及波形显示。考虑待测流体运动频率基本在50 Hz以内[18]，同时为了保证对气液两相流相关流速的有效跟踪测量，本次实验电导传感器采样频率设置为2000 Hz。此外，每个流动工况采样时间设置为30 s。环形电导传感器阵列测量系统如图2所示。

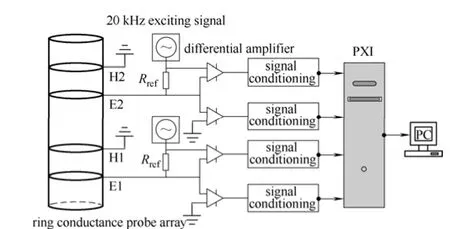
图2　环形电导传感器阵列测量系统Fig.2　Measurement system of ring shape conductance probe array

2　段塞流环形电导传感器阵列相关流速测量

图3为段塞流环形电导传感器阵列上下游信号及其互相关函数计算结果。段塞流典型流动特征表现为气塞与液塞沿管轴向交替运动。根据电导传感器测量电路原理，当激励电极与检测电极之间流体的导电性增强时，传感器输出电压值较低；当流体导电性减弱时，传感器测量电压值较高，即当段塞流中的气塞经过传感器时，传感器测量电压幅值在2 V左右；此外，由于气塞周围液膜厚度变化或液塞中分散气泡作用，电导传感器输出信号具有一定的波动性。

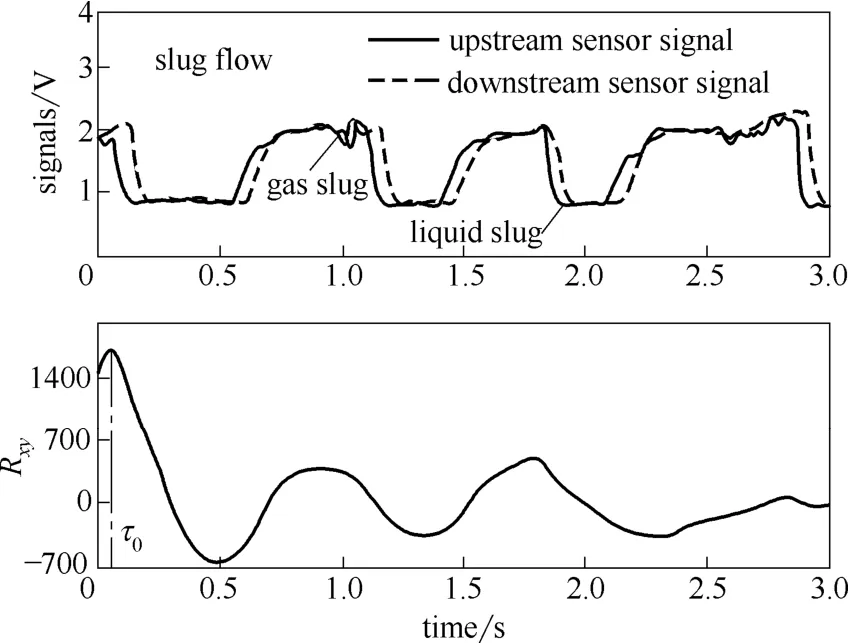
图3　段塞流电导传感器上下游信号及互相关函数Fig.3　Signals between upstream and downstream conductance probes and its cross-correlation function under slug flow(Usg=0.055 m·s-1,Usw=0.037 m·s-1)

本文采用互相关算法[19-20]计算延迟时间。假设上游传感器输出为x(t)，下游传感器输出为y(t)，下

游传感器输出相对x(t)在时间上滞后t0。x(t)和y(t)的互相关函数Rxy(t)可表示为

当t= t0时，Rxy(t)达到最大值。已知上下游传感器间距L，则气液两相流相关流速为

其中，上下游传感器间距L=0.03 m。图4是气相表观流速Usg分别为0.055、0.074、0.147、0.221、0.295 m·s-1时，随液相表观流速Usw逐渐增大的上游电导传感器测量信号变化。可以看出，随着水相表观速度增大，由于液相湍动作用增强，气塞长度趋于变短，气塞与液塞交替频率也趋于增大。

3　快关阀截取持气率数值模拟

快关阀截取段塞流持气率数值模拟流程如图5所示。

其持气率波动序列具体计算步骤如下。

（1）含泡液塞持气率模拟计算。首先，从环形电导传感器上游信号中判断气塞与液塞。根据实验测量数据，选取判别阈值为1.2 V，当测量电压大于1.2 V时，判定为气塞经过传感器；当测量电压小于1.2 V时，判定为液塞经过传感器，进而将段塞流测量信号划分为气塞与液塞交替序列。然后，提取液塞部分测量电压的平均值，根据液塞部分测量电压及全水时测量电压，再利用Maxwell方程估算含泡液塞部分的持气率值。由Maxwell方程可得含泡液塞持气率与混合电导率关系为

图4　上游电导传感器信号随水相表观流速变化Fig.4　Signals of upstream conductance probe versus superficial water velocity

式中，sw和sm分别为全水及含泡液塞电导率，Ys为液塞持气率，则持水率Yw=1-Ys，将其代入式(3)可得持水率Yw与含泡液塞电导率之间关系

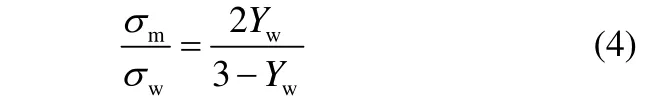
根据本文电导传感器测量电路原理，传感器输出电压与混合流体电导率呈反比，即

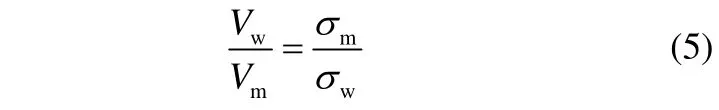
式中，Vw和Vm分别为全水及液塞的传感器输出电压平均值。将式(4)及式(5)联立可得液塞持气率表达式

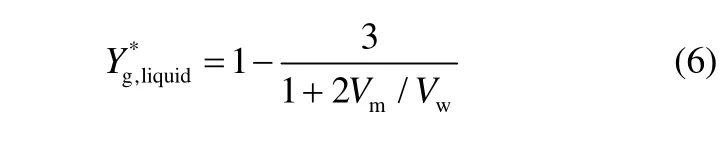
式中，Y*g,liquid为段塞流液塞部分持气率，Y*=1-Y。

g,liquidw

图5　快关阀截取持气率数值模拟流程Fig.5　Flow chart of QCV’s gas holdup acquisition by numerical simulation

（2）气塞与液塞长度模拟计算。基于环形电导传感器阵列上下游信号提取两相流相关流速。为减小相关流速测量误差，本文选取30000点数据长度进行互相关函数计算，以1000点为步长，逐步计算不同时间段内互相关函数的延迟时间，计算结果表明所有流动工况下延迟时间序列标准差均小于0.002，说明采用该方法计算的传感器上下游信号延迟时间较为稳定。最后基于延迟时间序列平均值及式(2)计算两相流相关速度。

根据两相流相关速度，结合步骤（1）得到的气塞和液塞交替时间序列，可得到流体流过上游传感器时对应的气塞与液塞交替的长度序列。图6列出了不同段塞流流动工况计算所得的气塞与液塞交替的长度序列，所有序列的持续时间均为25 s。

如图6所示，同一流动工况下气塞与液塞交替出现的长度均存在一定程度波动，表现为复杂的段塞流空间流动结构拟周期运动现象。当固定气相表观流速时，随着水相表观流速逐渐增加，液相湍动作用增强，长气塞被击碎为较短气塞，气塞的平均长度减小，相同时间内气塞个数增加，相应的液塞个数也增多，液塞平均长度也具有减小趋势，但没有气塞长度变化明显。当固定水相表观流速时，随着气相表观流速增加，气塞长度逐渐增大，而液塞长度增加较少，此时气塞长度明显大于液塞长度。

（3）快关阀门间距对截取持气率影响的模拟计算。以一定步长（本文设定步长为气塞平均长度的0.1倍）逐步移动快关阀截取流体序列的位置，计算每次截取得到的气塞和液塞长度占比，按比重加权计算持气率，气塞权值设为1，液塞权值为步骤（1）中所得液塞部分的视持气率Y*g,liquid。由此得到该快关阀门间距下模拟截取持气率的序列。

（4）快关阀门间距及截取次数对持气率影响的模拟计算。改变快关阀门间距，重复步骤（3）可得不同快关阀门间距时模拟持气率序列。根据简单随机抽样中重复抽样原则，样本容量计算公式如下[21]

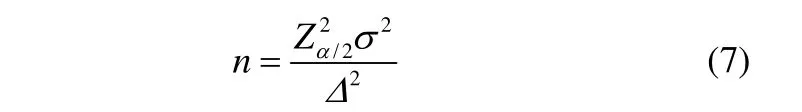
式中，n是需要样本量，即本文中快关阀截取次数；Za/2表示1-a置信水平下的Z统计量，如本文选取95%置信水平的Z统计量为1.96；s表示总体的标准差；D是允许误差，本文设置为5%。图7所示为Usg=0.055 m·s-1和Usw=0.037 m·s-1时，快关阀间距从0.5 m增加到4.0 m时模拟得到的持气率序列。随着快关阀间距增大，模拟持气率序列的波动逐渐减小，其序列标准差亦减小。

由式(7)计算各段塞流下不同阀门间距所需的截取次数结果如图8所示。结果表明随着快关阀门间距增大，所需截取次数逐渐减小。当阀门间距较小时，截取次数随着阀门间距增大迅速减小，减小速率随着阀门间距增大逐渐降低。在95%置信水平、允许误差为5%情况下，如果截取次数选为3，则需要快关阀门间距至少大于1 m，且随着气相表观流速的增大，所需阀门间距呈现逐渐增大的趋势。具体而言，当水相表观流速为0.037 m·s-1时，随着气相表观流速从0.055 m·s-1增加到0.295 m·s-1，采用3次快关阀截取所需的快关阀门间距从1.3 m增大到1.8 m左右。当水相表观流速为0.074 m·s-1和0.147 m·s-1时，随着气相表观流速增大，采用3次快关阀截取所需的快关阀门间距从小于1.5 m增大到2.0 m左右。这是由于相同水相表观速度下，增大气相表观速度导致气塞变长，使得流体结构在时间尺度上更加不均匀，快关阀截取到气塞或液塞所占比重具有明显差异，从而模拟计算的持气率序列标准差增大，相同截取次数所需的快关阀间距增大。

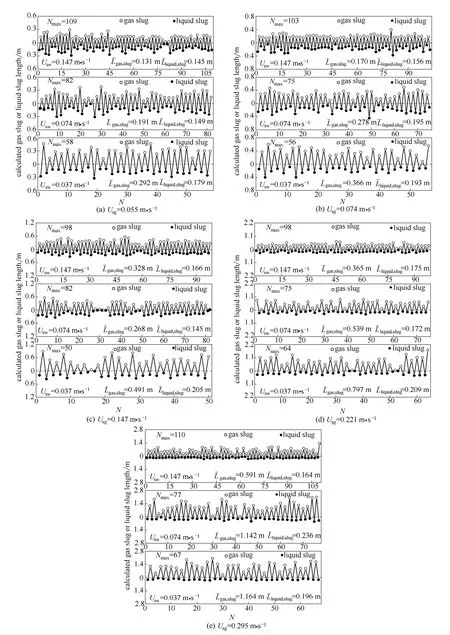
图6　不同段塞流气塞和液塞交替长度序列Fig.6　Length series of alternant gas and liquid slugs under different slug flow conditions

反之，当气相表观流速固定，增加水相表观流速，气塞长度变短，使得气塞与液塞交替时间变短，流体结构在时间尺度上更加均匀，最终导致相同截取次数所需的快关阀间距减小。如当气相表观流速为0.055 m·s-1时，随着水相表观流速从0.037 m·s-1增加到0.147 m·s-1，采用3次快关阀截取所需的快关阀门间距从1.3 m减小到1.1 m左右。当气相表观流速分别为0.074、0.147、0.211、0.295 m·s-1时，随着水相表观流速增大，采用3次快关阀截取所需的快关阀门间距呈现不同程度的减小。

图7　段塞流下快关阀间距变化时的持气率波动序列Fig.7　Gas holdup fluctuation series of slug flow with changes of spacing between valves(Usg=0.055 m·s-1,Usw=0.037 m·s-1)

4　实验验证及误差分析

为了验证快关阀法模拟计算结果可行性，本文选取Usg=0.221 m·s-1、Usw=0.037 m·s-1和Usg=0.074 m·s-1、Usw=0.074 m·s-1两个段塞流流动工况进行快关阀截取实验。本次验证实验在图1实验装置上进行改装，在距离入口0.75 m处安装上游快关阀，上下游快关阀间距设置为1.55 m。对每个流动工况，待流体流动稳定后同时关闭上下游快关阀。通过引流管将快关阀间液体导入量筒中测量体积，根据快关阀间总体积计算持水率，进而获得持气率。每个流动工况下分别截取快关阀50次，以获得足够样本数据。验证实验所得持气率数据如图9所示。

在Usg=0.221 m·s-1、Usw=0.037 m·s-1流动工况下，实验获得的持气率序列标准差为0.0296；在Usg=0.074 m·s-1、Usw=0.074 m·s-1流动工况下，实验获得的持气率序列标准差为0.0213。根据式（7）计算的两个流动工况在95%置信度及5%允许误差情况下需要的快关阀截取次数分别为2次和1次。如果按照前面快关阀持气率模拟计算方法，上述两个流动工况在快关阀间距为1.55 m时所需截取次数分别为6次和3次，其实验所得最低截取次数小于模拟计算得到的次数。分析二者之间差异的来源，一方面是由于实验中在人工快关阀关断时可能产生不同步关断误差，另一方面模拟计算方法也存在一定偏差。在模拟计算中，假设气塞持气率为1，由于忽略了气塞周围液膜及液滴存在，在模拟计算中会导致持气率序列存在一定误差。此外，在采用Maxwell方程计算含泡液塞持气率时，气液两相流分散相非均匀分布及泡径大小变化也会导致模拟的持气率序列存在一定误差。

以下对气塞与液塞权系数影响进行分析。假设对于序列中一段时间，从t1到t2，计算得到的气塞占比为a，液塞占比为b，从而a+b=1。设气塞和液塞平均持气率分别为yg,slug和yg,liquid，则该时间段内持气率为

对于整个时间序列，计算每一次截取所得的气液比例，假设比例序列分别为[a1,a2,…,an]和[b1,b2,…,bn]，对应ai+bi=1，i=1,2,…,n。设持气率序列为[Y*g1，Y*g2,…,

Y*

gn]，其中，Y*gi=aiyg,slug+biyg,liquid，结合ai+bi=1，可表示为Y*gi= yg,liquid+ai(yg,slug-yg,liquid)。则持气率序列的平均值和标准差分别为

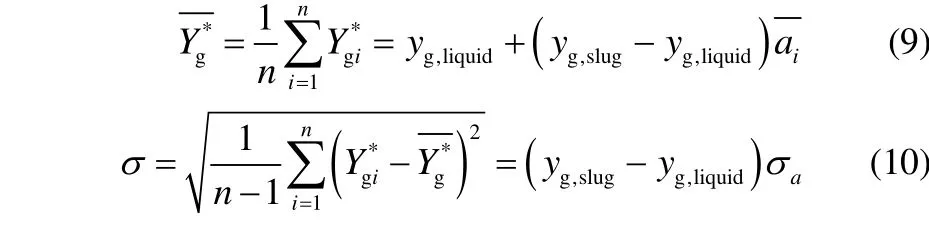
图8　段塞流情况下快关阀截取次数随快关阀间距变化趋势Fig.8　Trend of trapping numbers with changes of spacing between valves under slug flows

需要说明的是，对混状流持气率快关阀优化设计时，需对混状流流经传感器测量部分的气块设置合适权值，一般气块流经传感器的输出电压较段塞流气塞要低，使用权值1仍然是充分条件，但由此引入的误差也较大。对于泡状流，由于流体在时间和空间上分布都比较均匀，在保证快关阀同时关断的前提下，所需的快关阀门间距明显短于段塞流和混状流情况。calibration method for measuring liquid film thickness [J]. Int. J. Multiphase Flow，1992，18(3): 423-437. DOI: 10.1016/0301-9322(92)90026-D.

[3] TSOCHATZIDIS N A，KARAPANTSIOS T D，KOSTOGLOU M V，et al. A conductance probe for measuring liquid fraction in pipes and

图9　快关阀多次截取持气率误差波动Fig.9　Error fluctuation of QCV’s gas holdup at multiple trapping number(slug flow，LQCV=1.55 m)

5　结　论

（1）本文运用两相流相关测速法对环形电导传感器阵列信号进行了处理，计算提取了段塞流中的气塞与液塞轴向长度序列，采用Maxwell方程计算了含泡液塞持气率，根据气塞与液塞在段塞流长度序列中占比，加权计算得到了段塞流持气率波动序列，为气液两相段塞流快关阀法持气率测量提供了理论分析基础。

（2）对模拟计算获得的段塞流持气率波动序列进行了统计分析，对段塞流不同快关阀间距时获得95%置信度及5%允许误差所需的截取次数进行了预测，当水相表观速度一定时，随着气相表观速度增大，其相同截取次数所需的快关阀门间距呈增大趋势；当气相表观流速一定时，随着水相表观流速增大，其相同截取次数所需的快关阀门间距呈减小趋势。该结论为提高快关阀法测量段塞流持气率精度提供了实验设计依据。

References

[1] DYKESTEEN E，HALLANGER A，HAMMER E，et al. Non-intrusive three-component ratio measurement using an impedance sensor [J]. J. Phys. E.，1985，18(6): 540-544. DOI: 10.1088/0022-3735/18/6/017.

[2] KANG H C，KIM M H. The development of a flush-wire probe and packed beds [J]. Int. J. Multiphase Flow，1992，18(5): 653-667. DOI: 10.1016/0301-9322(92)90037-H.

[4] FOSSA M. Design and performance of a conductance probe for measuring the liquid fraction in two-phase gas-liquid flows [J]. Flow Meas. Instrum.，1998，9(2): 103-109. DOI: 10.1016/S0955-5986(98)00011-9.

[5] LUCAS G P，CORY J C，WATERFALL R C. A six-electrode local probe for measuring solids velocity and volume fraction profiles in solids-water flows [J]. Meas. Sci. Technol.，2000，11(10): 1498-1509. DOI: 10.1088/0957-0233/11/10/311.

[6] LUCAS G P，JIN N D. A new kinematic wave model for interpreting cross correlation velocity measurements in vertically upward bubbly oil-in-water flows [J]. Meas. Sci. Technol.，2001，12(9): 1538-1545. DOI: 10.1088/0957-0233/12/9/321.

[7] ODDIE G，SHI H，DURLOFSKY L J，et al. Experimental study of two and three phase flows in large diameter inclined pipes [J]. Int. J. Multiphase Flow，2003，29(4): 527-558. DOI: 10.1016/S0301-9322(03)00015-6.

[8] YE J M，PENG L H，WANG W R，et al. Helical capacitance sensor-based gas fraction measurement of gas-liquid two-phase flow in vertical tube with small diameter [J]. IEEE Sens. J.，2011，11(8): 1704-1710. DOI: 10.1109/JSEN.2010.2095004.

[9] YE J M，PENG L H，WANG W R，et al. Optimization of helical capacitance sensor for void fraction measurement of gas-liquid two-phase flow in a small diameter tube [J]. IEEE Sens. J.，2011，11(10): 2189-2196. DOI: 10.1109/JSEN.2011.2116115.

[10] 张立峰，王化祥. 一种新的电容层析成像电极组合激励测量模式[J]. 化工学报，2012，63(3): 860-865. DOI: 10.3969/j.issn.0438-1157. 2012.03.026. ZHANG L F，WANG H X. A new combined-electrode exciting-measuring mode for electrical capacitance tomography [J]. CIESC Journal，2012，63(3): 860-865. DOI: 10.3969/j.issn.0438-1157. 2012.03.026.

[11] 罗琴，赵银峰，叶茂，等. 电容层析成像在气固流化床测量中的应用 [J]. 化工学报，2014，65(7): 2504-2512. DOI: 10.3969/j.issn. 0438-1157.2014.07.012. LUO Q，ZHAO Y F，YE M，et al. Application of electrical capacitance tomography for gas-solid fluidized bed measurement [J]. CIESC Journal，2014，65(7): 2504-2512. DOI: 10.3969/j.issn.0438-1157.2014.07.012.

[12] CARTELLIER A. Optical probes for local void fraction measurements: characterization of performance [J]. Rev. Sci. Instrum.，1990，61(2): 874-886. DOI: 10.1063/1.1141457.

[13] MACCHI A，GRACE J R，BI H. Use of ultrasound for phase holdup measurements in multiphase systems [J]. Can. J. Chem. Eng.，2001，79(4): 570-578. DOI: 10.1002/cjce.5450790415.

[14] ZHENG Y，ZHANG Q K. Simultaneous measurement of gas and solid holdups in multiphase systems using ultrasonic technique [J]. Chem. Eng. Sci.，2004，59(17): 3505-3514. DOI: 10.1016/j.ces. 2004.05.016.

[15] JANA A K，DAS G，DAS P K. Flow regime identification of two-phase liquid-liquid upflow through vertical pipe [J]. Chem. Eng. Sci.，2006，61(5): 1500-1515. DOI: 10.1016/j.ces.2005.09.001.

[16] JIN N D，XIN Z，WANG J，et al. Design and geometry optimization of a conductivity probe with a vertical multiple electrode array for measuring volume fraction and axial velocity of two-phase flow [J]. Meas. Sci. Technol.，2008，19(4): 334-340. DOI: 10.1088/0957-0233/ 19/4/045403.

[17] CHENG W，LIU W H，HU B W，et al. Experimental study on gas-liquid two-phase flows in an areation tank by using image treatment method [J]. J. Hydrodyn.，2008，20(5): 650-655. DOI: 10.1016/S1001-6058(08)60108-0.

[18] 赵安，韩云峰，翟路生，等. 气液两相流电容传感器相浓度测量特性 [J]. 化工学报，2015，66(7): 2402-2410. DOI: 10.11949/j.issn. 0438-1157.20150166. ZHAO A，HAN Y F，ZHAI L S，et al. Characteristics of phase-concentration measurement for capacitance sensors in gas-liquid two-phase flow [J]. CIESC Journal，2015，66(7): 2402-2410. DOI: 10.11949/j.issn.0438-1157.20150166.

[19] BECK M S. Correlation in instruments: cross correlation flowmeters [J]. J. Phys. E.，1981，14(1): 7-19. DOI: 10.1088/0022-3735/14/1/001. [20] THORN R，BECK M S，GREEN R G. Non-intrusive methods of velocity measurement in pneumatic conveying [J]. J. Phys. E.，1982，15(11): 1131-1139. DOI: 10.1088/0022-3735/15/11/001.

[21] 陈克明，宁震霖. 市场调查中样本容量的确定 [J]. 中国统计，2005，3: 16-17. CHEN K M，NING Z L. Determination of sample size in market research [J]. China Statistics，2005，3: 16-17.

Optimal design for measuring gas holdup in gas-liquid two-phase slug flow using quick closing valve method

ZHAO An，HAN Yunfeng，ZHANG Hongxin，LIU Weixin，JIN Ningde
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

Abstract:Quick closing valve (QCV) method is a common means of calibrating gas holdup in gas-liquid two-phase flow test. Unreasonable selections of spacing between valves and trapping times in QCV could bring about large error in gas holdup measurement，particularly since the gas slug and liquid slug in slug flow present flow characteristics with random variability. In this study，an optimal design was proposed for measuring gas holdup using QCV method. The cross-correlation velocity of gas-liquid two-phase slug flow was measured based on the signals between axially upstream and downstream probes. Then，the lengths of gas slug and liquid slug were extracted from the upstream probe signals under different flow conditions. Also，the gas holdup in liquid slugs was calculated by using Maxwell equation. On that basis，the gas holdup series was simulated at different spacing between valves based on the gas slug ratio in pipe. By analyzing the fluctuation of gas holdup series，the floor level of trapping times was indicated under the condition of 95% confidence coefficient and 5% permissible error at different spacing between valves. Finally，an experiment was conducted to assess the trapping times in QCV with the spacing setting at 1.55 m length. The measuring errors of gas holdup using QCV method was statistically analyzed，and it was proved that the design guideline provided a sufficient condition for setting up thespacing between valves.

Key words:gas-liquid two-phase flow；slug flow; gas holdup；QCV method

DOI：10.11949/j.issn.0438-1157.20151293

中图分类号：TP 212.9

文献标志码：A

文章编号：0438—1157（2016）04—1159—10

基金项目：国家自然科学基金项目（51527805，11572220）；国家科技重大专项（2011ZX05020-006）。

Corresponding author:Prof. JIN Ningde，ndjin@tju.edu.cn