考虑信号交叉口转向类型的最优路径规划算法*
周熙阳 杨兆升,2,3 张伟,2,4† 邴其春 商强
(1.吉林大学 交通学院, 吉林 长春 130022; 2.吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130022;
3.吉林大学 吉林省道路交通重点实验室,吉林长春 130022; 4.山东高速股份有限公司, 山东 济南 250014)
考虑信号交叉口转向类型的最优路径规划算法*
周熙阳1杨兆升1,2,3张伟1,2,4†邴其春1商强1
(1.吉林大学 交通学院, 吉林 长春 130022; 2.吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130022;
3.吉林大学 吉林省道路交通重点实验室,吉林长春 130022; 4.山东高速股份有限公司, 山东 济南 250014)
摘要:针对现有最优路径规划算法没有充分考虑不同转向类型的车辆在信号交叉口处的等待时间,导致算出的最优路径实际效果不佳等问题,提出了一种考虑信号交叉口转向类型的最优路径规划算法.首先,根据不同的转向类型构建了信号交叉口等待时间模型;然后,提出了一种改进的星型表,对路网中邻接路段之间的转向类型与相应参数进行表达和存储优化;在此基础上,提出了考虑信号交叉口转向类型的拓展A*算法(CMTA*算法),并进行了算例验证.结果表明,相比于传统算法和考虑信号交叉口等待时间的CWTSI-SP算法,CMTA*算法所计算出的最优路径时间费用更低,并且运算效率更高.
关键词:最优路径规划算法;交叉口;转向类型;等待时间;交通工程
最优路径规划是智能交通诱导系统研究中的一项重要内容.不同于一般抽象网络,城市路网包含大量动态交通信息与约束条件,研究如何在实际的城市路网中为驾驶员规划最优路径,保证路径行程时间最短,对提高出行效率具有重要意义.城市路网中,驾驶员于信号交叉口等待的时间在其行程时间中占较大比重,而大多数最优路径规划算法(包括标号法[1- 2]、启发式算法[3- 6]等)仅考虑了路段的行程时间,导致所求最优路径与实际最优路径之间存在较大差异.因此,需研究考虑信号交叉口等待时间的最优路径规划算法.
目前,国内外学者主要研究将信号交叉口延误叠加进最优路径规划算法[7- 10].信号交叉口延误一般通过延误模型求得.若路段划分时将交叉口作为路段的一部分,则路段平均行程时间已包含交叉口延误[11].但交叉口延误只能反映车流的总体特征,通常取均值,而每一辆车的实际等待时间会因所遇信号灯状态的不同而呈现出较大差异.同样的“最优路径”,若某驾驶员不幸频遇红灯,那么对他而言,该路径可能并非最优.针对这一问题,杨帆等[12]通过对单车信号交叉口等待时间进行建模,提出了一种考虑信号交叉口等待时间的标号算法(CWTSI-SP算法),并用一个算例证明该算法所求的最优路径更贴近驾驶员的实际情况.
但CWTSI-SP算法存在以下不足:①没有考虑车辆在交叉口处的转向类型.在实际中,车辆从当前交叉口驶向同一个下游交叉口,根据来向的不同,可能进行直行、左转和右转,其中左转和直行可能分属不同的相位,而右转因控制方式相对独立,故不属于任何一个相位.但CWTSI-SP算法将驶向同一个下游交叉口的车辆归入同一个相位,与实际中的信号相位形式不符.②CWTSI-SP算法将等待时间模型叠加进传统Dijkstra算法,导致算法运行时间慢于传统Dijkstra算法.
针对上述方法的不足之处,文中提出了考虑信号交叉口转向类型的最优路径规划算法.首先,根据不同的转向类型,构建了信号交叉口等待时间模型.然后,提出了一种改进的星型表对邻接路段之间的转向类型进行表达和存储,并在此基础上设计了一种考虑信号交叉口转向类型的拓展A*算法.
文中的研究重点为考虑不同转向类型的最优路径搜索,研究的假设前提如下:①路网交叉口采用单点信号控制,交叉口信号周期已知且固定;②各信号相位相互独立,且相位起始时刻已知;③路段行程时间固定.
1考虑转向类型的信号交叉口等待时间模型
在信号交叉口,右转车辆往往不受信号灯控制,在礼让行人的前提下可即时通行,部分信号交叉口有专门的右转信号灯(多见于冲突点密集的交叉口),通常红灯时间较短.因此,当其它通行方向因红灯必须停车等待时,右转车辆往往可以快速通过交叉口.在如图1所示的路网中(无右转信号灯),车辆从节点4出发,经节点5驶向节点3.当车辆于ta时刻到达节点5时,节点5的灯态为南北直行方向绿灯,根据等待时间的不同,驾驶员有3种可能的选择:①等待直行绿灯,路径为5- 6- 3;②等待左转绿灯,路径为5- 8- 9- 6- 3;③即刻右转,路径为5- 2- 3.
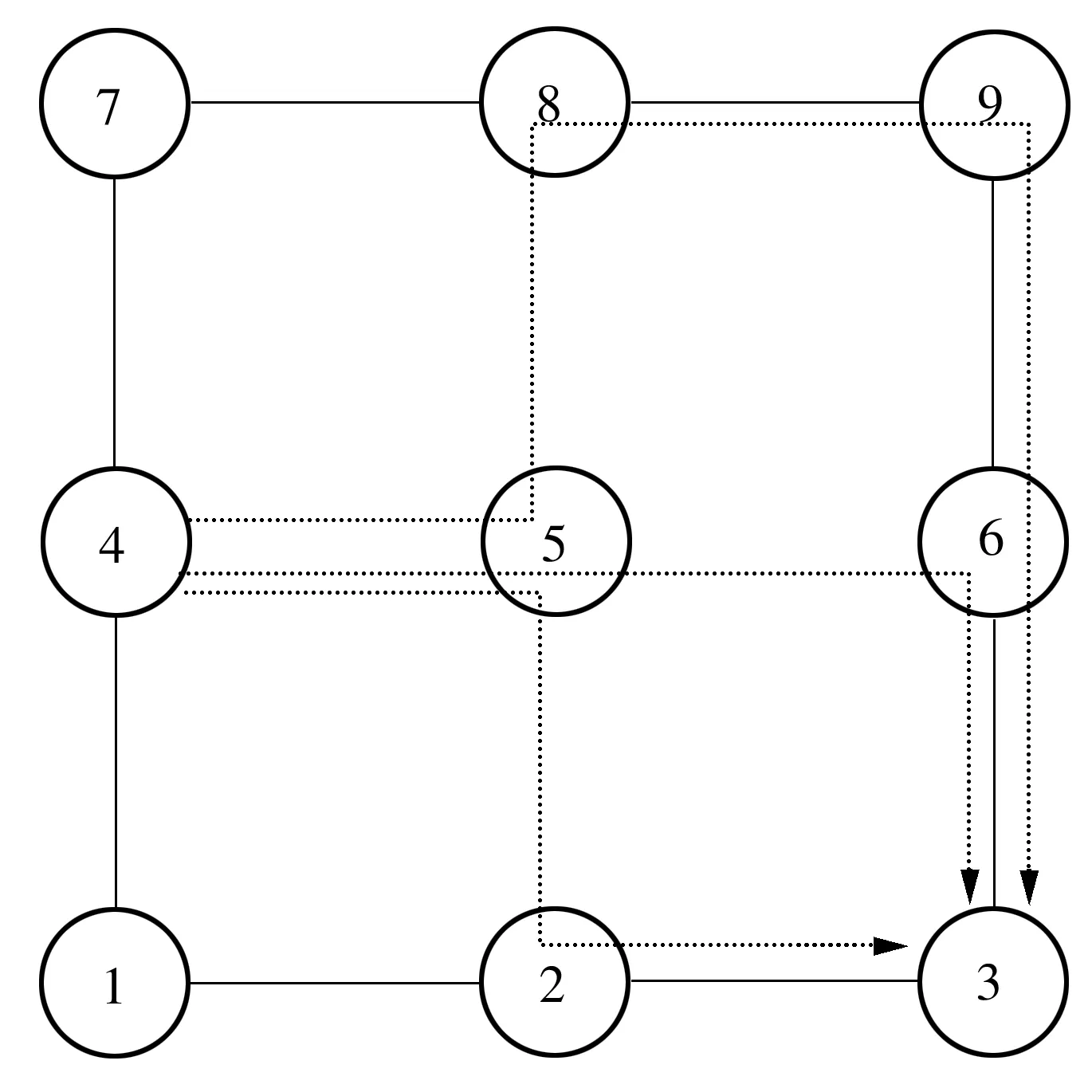
图1 路径选择示意图
机动车到达交叉口的时刻不同,所遇灯态也不同,因此等待时间随到达时刻发生变化.
ta,k=tl,k′+ωk′,k
(1)
tl,k′=ta,k′+tw,k′
(2)
式中,ta,k为到达节点k的时刻,tl,k′为离开上游节点k′的时刻,ωk′,k为有向路段k′,k的行程时间,tw,k′为节点k′的等待时间.
由于右转控制的特殊性,下面分右转与非右转两种情况对交叉口等待时间进行建模.
1.1右转等待时间
将有专门信号灯控制的右转定义为非自由右转,将没有专门信号灯控制的右转定义为自由右转,对两种右转分别进行讨论.
(1)非自由右转
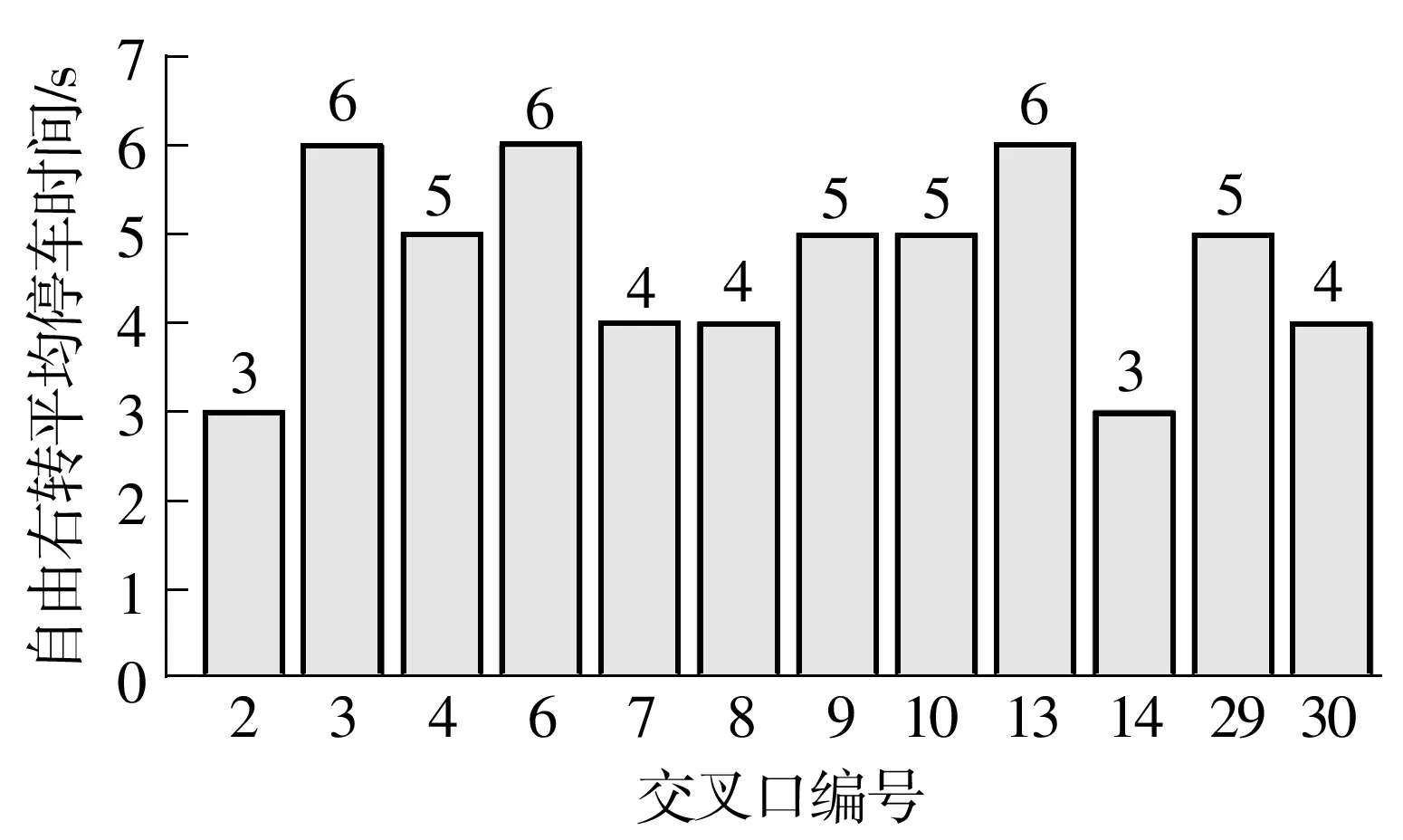
右转信号灯的信号配时如图2所示,若右转车辆在红灯期间到达,等待时间为红灯剩余时间;若右转车辆在绿灯期间到达,等待时间为0.
(3)
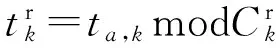
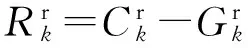
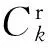
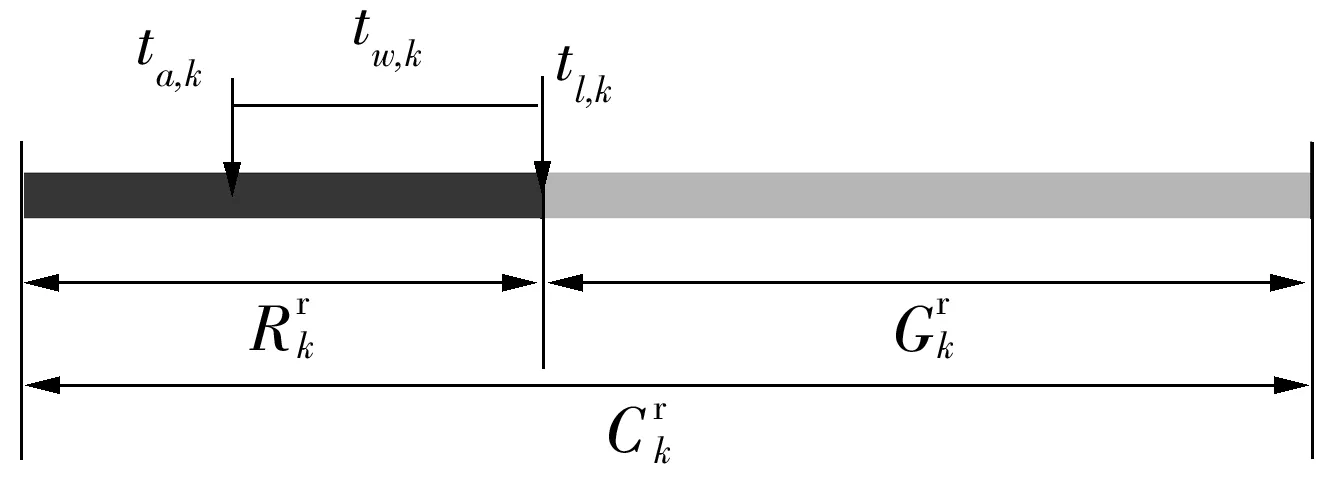
图2 非自由右转信号配时
(2)自由右转
在自由右转条件下,右转车辆不受路口红灯的限制,通常假设其tw,k为0,但在实际中,车辆右转时需给行人与非机动车流让行,因而会产生一定的随机等待时间.由于在无信号灯控制的条件下难以对每辆右转车的具体等待时间单独建模,因此,文中基于实际交通数据,为自由右转的车辆加上一个惩罚时间,从而对模型进行修正:
(4)

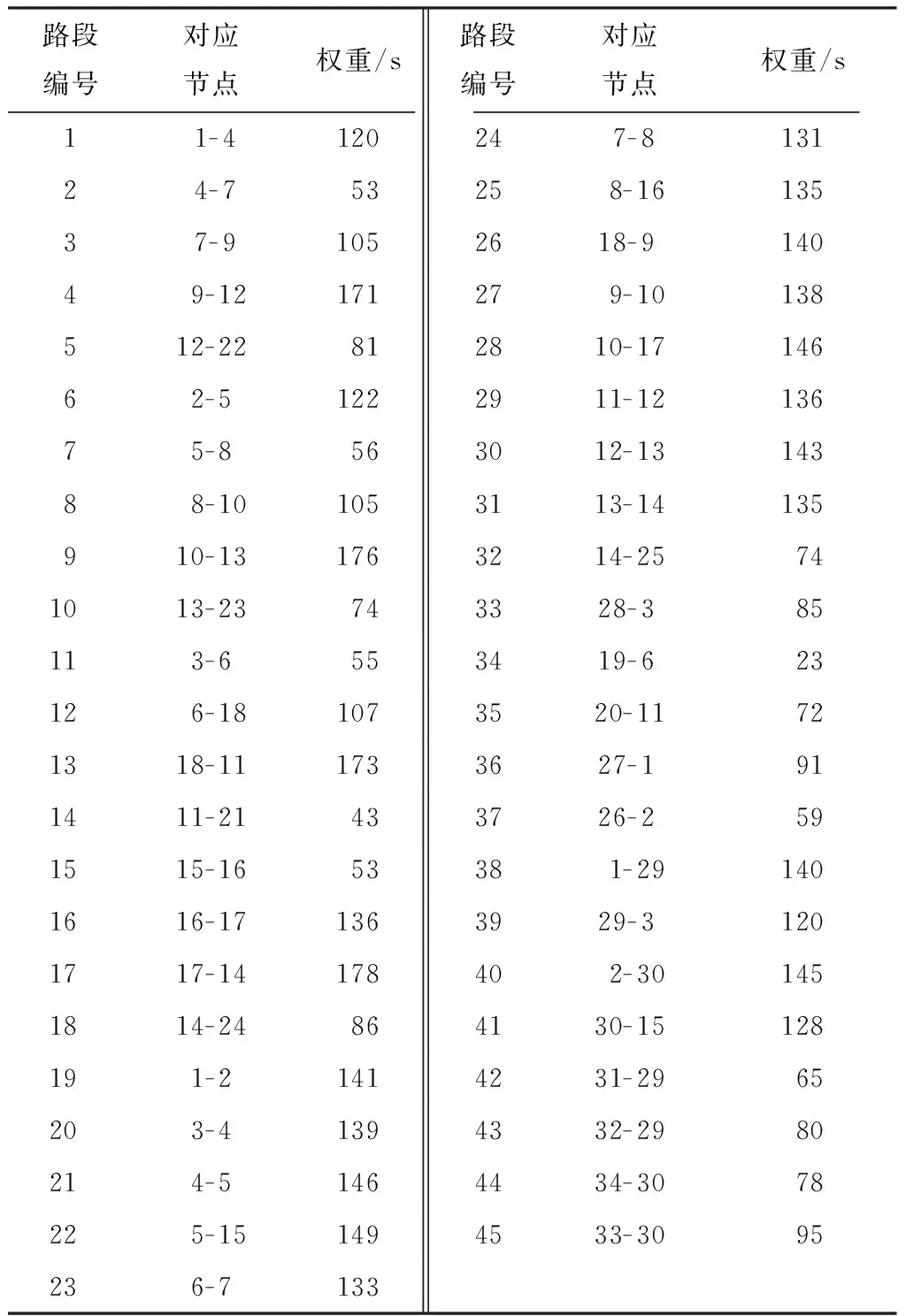
自由右转平均停车时间为自由右转车辆在停车线处的平均停车时间,由交通调查数据统计获得.处理时只统计在停车线处停车的右转车辆,因为后续车辆的排队时间仍属于路段行程时间.
由于右转车辆停车时间相对较短,往往能快速驶离交叉口,因此在交叉口处适当选择右转可显著缩短路径行程时间.
1.2非右转等待时间
非右转车辆包含直行车辆和左转车辆,它们共同接受信号灯控制,文献[12]中证明信号相位的切换将使等待时间发生突变,但其并未考虑两个相位之间的绿灯间隔时间(黄灯时间+全红时间).绿灯间隔时间内到达停车线的非右转车辆必须停车等待,因此绿灯间隔时间将影响等待时间的突变.文中考虑绿灯间隔时间,对非右转等待时间进行建模.
假设节点k共有N个信号相位,信号周期为Ck,绿灯间隔时间为h,车辆到达时相序为n,离开时相序为m.
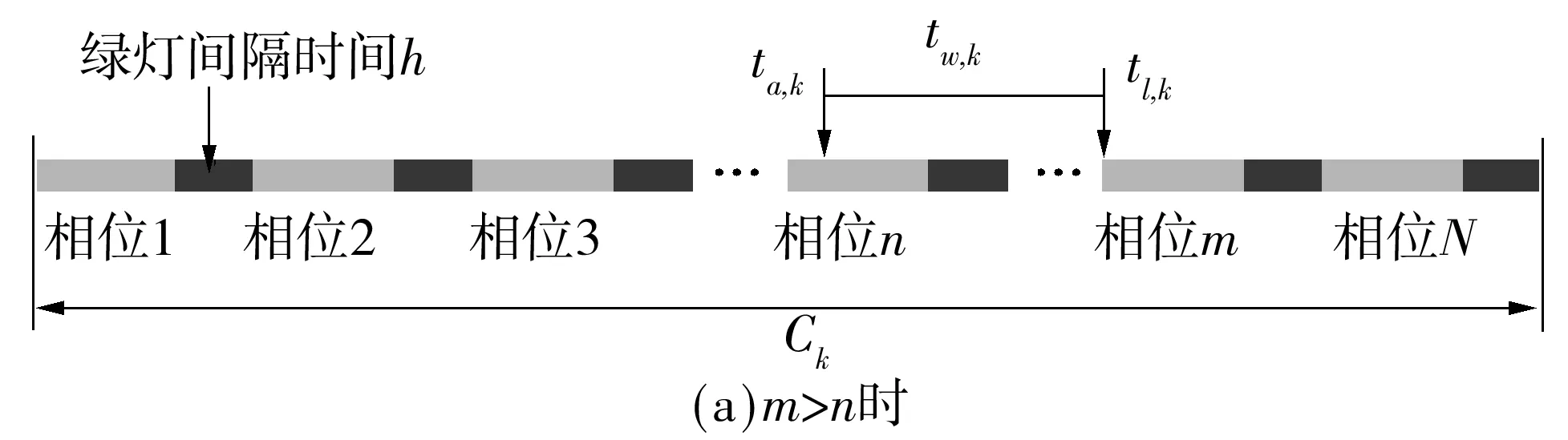

图3 非右转信号配时
(1)m>n时,如图3(a)所示,车辆可以在当前周期内离开.
(5)
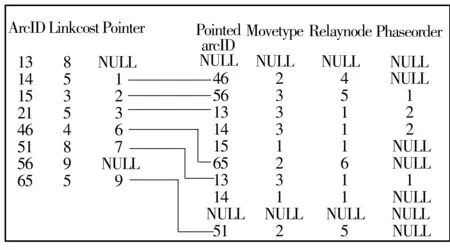
(2)m (6) (7) 显然,当m=n时,表示非右转车辆到达交叉口即遇到绿灯,此时tw,k为0. 2考虑转向类型的最优路径规划算法 2.1路网模型优化 为将文中的等待时间模型叠加进最优路径规划算法,路网模型必须能有效表达邻接路段之间的转向信息(为表述简便,界定“直行”也属于一种转向情况).Anez等[13]提出了对偶图表思想,将原图中的弧段映射为新图中的节点,而将原图中节点的转向映射为新图中的弧段,从而表达了路段之间的转向关系.但传统表达法(邻接矩阵、邻接表、星型表等)无法表达出邻接路段之间的转向类型(非自由右转、自由右转、非右转),以及其对应的交叉口相位相序. 文中提出一种改进的星型表,结合对偶图思想,以路段为存储对象,并引入3个数组:转向类型数组(Movetype)、末端节点数组(Relaynode)和相序数组(Phaseorder),从而表达邻接路段之间的转向类型、发生转向的节点以及转向所对应的相序. Movetype中存储的值为mtk,i,j,表示经节点k由路段i驶入路段j方向的转向类型:非自由右转则mtk,i,j=1,自由右转则mtk,i,j=2,非右转则mtk,i,j=3.称路段j为路段i的后继路段,节点k为路段i的末端节点,Relaynode中存储末端节点信息.Phaseorder中存储由路段i至路段j通行方向在节点k处所属的相序,由于相位相序仅针对非右转,故对于右转,赋值为NULL. 以图4所示的有向图为例,规定右转(2- 1- 5)和(5- 1- 4)为非自由右转,其余右转为自由右转,用改进的星型表对其进行表达,如图5所示. 图4 示例路网 图5 改进的星型表结构 图5中,数组ArcID存储路段信息,在该例中,路段13表示从节点1至节点3的路段,以此类推.数组Linkcost存储路段权重.数组Pointer存储指针,初始指向每一条路段的第一条后继路段所在地址.数组PointedarcID储存后继路段信息,每一条路段的后继路段按ArcID中的顺序排列.以路段21为例,路段权重为5,共3条后继路段:13、14、15,末端节点皆为节点1,故在Relaynode中皆赋值为1,指针指向路段13;21- 13为左转,对应节点1相位2,21- 14为直行,同样对应节点1相位2,21- 15为非自由右转,不分相位,故在Movetype中依次赋值为3,3,1,在Phaseorder中依次赋值为2,2,NULL.由于路段13、56无后继路段,故指针及其后续信息皆悬空,赋值为NULL. 以节点1为例,从图5中可看出节点1共有2个相位,第1相位为51- 13,第2相位为21- 13、21- 14同时放行,因此该星型表可以表达一个相位多种通行方向的情况.节点所包含的配时参数信息如表1所示. 表1 节点信号配时参数 表1中,若节点k为自由右转控制,则右转信号周期与右转绿灯时长皆赋值为NULL,若为非自由右转,则自由右转惩罚值为NULL.黄灯时长与全红时长之和为绿灯间隔时间,其取值由交管部门确定,一般黄灯时长3 s,全红时长2~3 s. 结合改进的星型表与节点配时参数表,即可完整表达与存储邻接路段间的转向类型、对应节点、对应相序,以及对应节点的具体配时信息,为最优路径规划算法计算交叉口等待时间提供条件.同时,改进的星型表存储了路段与节点之间的映射关系,通过指针可快速定位到节点,从而减小搜索空间,提高算法的搜索效率. 2.2考虑转向类型的拓展A*算法 A*算法是一种启发式搜索算法,利用估价函数限制搜索范围,具有搜索效率高,易于实现等优点.一般的A*算法并没有考虑信号交叉口等待时间,文中基于等待时间模型对A*算法进行拓展,提出考虑转向类型的A*算法(CMTA*算法). 在改进星型表的基础上,CMTA*算法由路段搜索节点.为便于描述,引入“弧节点”概念,定义如下:弧节点j即为以路段j为前驱路段的末端节点k(j).CMTA*算法的估价函数如式(8)所示. (8) 式中,f(j)为弧节点j的估价值,g(j)为从初始弧节点j到达弧节点的实际费用,ta,k(o)为初始弧节点的到达时刻,为已知量,ta,k(j)、ta,k(i)分别为弧节点j和弧节点i的到达时刻(弧节点j为弧节点i的后继弧节点),tl,k(i)为弧节点i的离开时刻,ωj为弧节点j的权重,即路段j的行程时间,tw,k(i)为弧节点i的交叉口等待时间,h(j)为弧节点j到目标弧节点的估计费用,D(j)为弧节点j与目标弧节点的欧式距离,Vmlim为路网最高限速值. 为保证找到最优路径,h(j)必须小于等于弧节点j到目标弧节点的实际费用.由于路网中两点之间的欧式距离最短,将其比上全路网的最高限速值,所得的行程时间必定小于实际行程时间. CMTA*算法具体步骤如下: 步骤1初始化,将所有弧节点的估价值f和实际费用g设为无穷,清空OPEN表和CLOSE表; 步骤2将初始弧节点加入OPEN表,并作为当前弧节点i,更新g(i)=0,然后将弧节点i从OPEN表移入CLOSE表; 步骤3将弧节点i的后继弧节点加入OPEN表,若后继弧节点已在CLOSE表中,则不加入; 步骤4对OPEN表中弧节点i的每一个后继弧节点j,按以下步骤计算f(j): (1)按式(9)计算弧节点i的到达时刻ta,k(i): ta,k(i)=g(i)+ta,k(o) (9) (2)对mtk,i,j进行判断:若mtk,i,j=1,按式(3)计算tw,k(i),转步骤(4);若mtk,i,j=2,按式(4)计算tw,k(i),转步骤(4);若mtk,i,j=3,转步骤(3); (4)按下式计算弧节点j当前实际费用g(j): g(j)=g(i)+tw,k(i)+ωj (10) 若当前g(j)小于原先值,则更新g(j),并按式(8)计算f(j);否则g(j)、f(j)保留原值; 步骤5对OPEN表中所有弧节点的估价值f进行排序,选择f最小的弧节点,将其作为当前弧节点i,并从OPEN表移入CLOSE表; 步骤6终止条件判别,若目标弧节点移入CLOSE表,表明找到最优路径,转步骤7;若OPEN表已空,且CLOSE表中没有目标弧节点,表明目标弧节点不可达,没有最优路径,算法终止;若非上述两种情况,转步骤3; 步骤7从目标弧节点回溯,输出最优路径,并顺序输出路径上所有末端节点,算法终止. CMTA*算法在A*算法的基础上叠加了信号交叉口等待时间模型,利用A*算法的启发性进行有向搜索,避免了传统标号算法必须遍历到目标节点的缺陷,提高了路径规划的效率.同时,CMTA*算法充分考虑了信号交叉口的控制方式与配时参数,在进行最优路径规划时根据车辆在交叉口处可能存在的各种转向类型,分别计算相应的交叉口等待时间,并以此作为路径费用的一部分,是一种考虑了交通控制系统的诱导算法. 3算例验证 以某城市试验区路网为算例路网,如图6所示. 该路网包含45条路段、20个参与试验的信号交叉口(以黄点标出),其中十字交叉口16个,T型交叉口4个,其坐标通过谷歌电子地图提取.算例条件设置如下. 图6 算例路网示意图 (1)路网边缘的14条路段为单向通行,以驶入路网为允许方向,其余29条路段为双向通行,两个方向权重相等,如表2所示.路网最高限速值设为70 km/h. 表2 路段权重表 (2)20个试验交叉口中,12个交叉口为自由右转(编号2、3、4、6、7、8、9、10、13、14、29、30),其余交叉口为非自由右转.文中通过视频调查数据对这12个交叉口的自由右转平均停车时间进行统计,取正常工作日早高峰25个周期的均值(取整)为统计结果,如图7所示. 图7 自由右转平均停车时间统计 (3)对所有试验交叉口的相位相序作统一规定:十字交叉口为4相位,相位1为南北向直行,相位2为东西向直行,相位3为南北进口左转,相位4为东西进口左转;15、16、17三个T型交叉口为2相位,相位1为南北向直行+南进口左转,相位2为西进口左转;18号交叉口为2相位,相位1为南北向直行+北进口左转,相位2为东进口左转. (4)设定起始点到达时刻与信号灯启动时刻均为0,非右转信号灯从相位1开始运行,右转信号灯从红灯启亮开始运行.交叉口的具体配时参数如表3所示. 选择80组具有一定距离且不在一条干线上的OD点对作为试验OD对.将文中提出的CMTA*算法与传统Dijkstra算法、文献[12]提出的CWTSI- SP算法进行对比,分别用3种算法计算出试验OD对间的最优路径,然后计算每条路径的总费用(路径总费用=路段权重之和+路径上所有交叉口的等待时间之和).按路径总费用对80组试验结果进行排序整理,如图8所示. 从图8中可看出以下两点: 1)对于同一对OD,用Dijkstra算法所计算的最优路径实际费用最高.这是由于Dijkstra算法并没有考虑信号交叉口等待时间,计算出的路径在交叉口处耗费了较多时间.其他两种算法考虑了信号交叉口等待时间,因此计算出的路径实际费用更低.并且,当OD对距离增大或受信号配时影响而导致路径费用升高时,CWTSI-SP算法与CMTA*算法的优势也愈加明显. 表3 交叉口信号配时表 图8 3种算法路径总费用对比 2)与CWTSI-SP算法相比,CMTA*算法所计算的路径实际费用更低.这是由于CWTSI-SP算法虽然考虑了信号相位,但没有考虑绿灯间隔时间,且没有考虑转向类型,运算过程中会将本向右转归入垂直方向直行相位或对向左转相位(由哪个相位更靠前决定),使计算结果产生偏差.CMTA*算法考虑了转向类型与绿灯间隔时间,能够准确地根据转向类型计算相应的等待时间,使计算出的最优路径更符合实际.例如,第80号试验OD对为11- 30(由西进口进入起点),CWTSI-SP算法所得路径为:11- 12- 13- 14- 17- 16- 15- 30,路径中包含3个周期较小的T型交叉口,但没有右转,路径费用为1 107 s,CMTA*算法所得路径为11- 14- 9- 7- 8- 5- 15- 30,包含3个右转,路径费用为934 s,明显优于CWTSI-SP算法. 图9为3种算法的性能对比.在80条路径的平均费用方面,CMTA*算法比Dijkstra算法降低了27.1%,比CWTSI-SP算法降低了13.7%;在80条路径的运算总时间方面,CMTA*算法比dijkstra算法降低了24.3%,比CWTSI-SP算法降低了34.9%.由于CWTSI-SP算法是在dijkstra算法的基础上叠加等待时间模型,因此运行时间大于一般dijkstra算法,而CMTA*算法以A*算法为基础,具有启发性,且采用改进的星型表优化了路网表达与存储结构,因此搜索效率更高.综上所述,CMTA*算法的性能优于其他两种算法. 图9 3种算法综合性能对比 4结语 文中提出了考虑信号交叉口转向类型的最优路径规划算法.通过对不同的转向类型进行分析,构建了信号交叉口等待时间模型,并提出了一种改进的星型表,使路网模型能够表达等待时间模型所需的参数,并在此基础上提出了基于等待时间模型的CMTA*算法.算例验证表明,CMTA*算法的运行效果要优于传统dijkstra算法与考虑信号交叉口等待时间的CWTSI-SP算法,不仅计算出的最优路径行程时间更小,且运算时间更低. 后续研究主要包括以下3个方面:①文中自由右转平均停车时间采用实际调查统计数据,而在大范围路网条件下进行交通调查需消耗较大的人力物力,下一步将研究自由右转停车模型,对自由右转的平均停车时间进行估算;②文中算法没有考虑交叉口协调控制的情况,下一步将针对此种情况,引入相位差参数,对算法进行改进;③为进一步提高算法运行效率,下一步将研究比A*算法更为高效的算法作为依托算法. 参考文献: [1]KLUNDER G A,POST H N.The shortest path problem on large-scale real-road networks [J].Networks,2006,48(4):182- 194. [2]徐长斌,刘艳梅.动态路径诱导算法研究 [J].公路交通科技:应用技术版,2007,10(1):35- 36. XU Chang-bin,LIU Yan-mei.The research of algorithm on dynamic path guidance [J].Journal of High-way and Transportation Research and Development:Applied Technique,2007,10(1):35- 36. [3]KIM Jinha,HAN Wook-Shin.Processing time-dependent shortest path queries without pre-computed speed information on road networks [J].Information Sciences,2014,255(1):135- 154. [4]韩李涛,牟乃夏.一种基于分层结构的最优路径算法 [J].山东科技大学学报(自然科学版),2013,32(3):77- 82. HAN Li-tao,MOU Nai-xia.An optimal path algorithm based on hierarchical structure [J].Journal of Shandong University of Science and Technology(Natural Science Edition),2013,32(3):77- 82. [5]杨庆芳,梅朵.基于云计算的城市路网最短路径遗传算法求解 [J].华南理工大学学报(自然科学版),2014,42(3):47- 58. YANG Qing-fang,MEI Duo.Cloud computing-based genetic algorithm to solve the shortest path in urban road networks [J].Journal of South China University of Technology(Natural Science Edition),2014,42(3):47- 58. [6]杜长海,黄希樾.改进的蚁群算法在动态路径诱导中的应用研究 [J].计算机工程与应用,2008,44(27):236- 239. DU Chang-hai,HUANG Xi-yue.Study on application of improved ant colony algorithm in dynamic route guidance [J].Computer Engineering and Applications,2008,44(27):236- 239. [7]FRANGIONI Antonio,GALLI Laura.Delay-constrained shortest paths:approximation algorithms and second-order cone models [J].Journal of Optimization Theory and Applications,2015,164(3):1051- 1077. [8]高淑萍,赵会宾.基于信号配时的动态路径诱导模型 [J].中国公路学报,2011,24(1):109- 114. GAO Shu-ping,ZHAO Hui-bin.Dynamic route guidance model based on signal lamp time assignment [J].China Journal of Highway and Transport,2011,24(1):109- 114.[9]黄美灵,陆百川.考虑交叉口延误的城市道路最短路径 [J].重庆交通大学学报(自然科学版),2009,28(6):1060- 1063. HUANG Mei-ling,LU Bai-chuan.Determination of the shortest path considering delays at intersections [J].Journal of Chongqing Jiaotong University(Natural Science Edition),2009,28(6):1060- 1063. [10]YANG Bai-yu,MILLER Elise.Adaptive routing considering delays due to signal operations [J].Transportation Research.Part B:Methodological,2003,38(5):385- 413. [11]李继伟.城市主次干路的路段行程时间估计与预测方法研究 [D].长春:吉林大学交通学院,2012. [12]杨帆,杨晓光.考虑信号交叉口等待时间的最短路径算法 [J].同济大学学报(自然科学版),2013,41(5):680- 686. YANG Fan,YANG Xiao-guang.Shortest path algorithm with a consideration of waiting time at signalized intersections [J].Journal of Tongji University(Natural Science Edition),2013,41(5):680- 686. [13]ANEZ J,DE La Barra T.Dual graph representation of transport networks [J].Transportation Research.Part B:Methodological,1996,30(3):209- 216. Optimal Route Planning Algorithm Considering Movement Type at Signal Intersections ZHOUXi-yang1YANGZhao-sheng1,2,3ZHANGWei1,2,4BINGQi-chun1SHANGQiang1 (1.College of Transportation, Jilin University, Changchun 130022, Jilin, China;2.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, Jilin, China;3. Jilin Province Key Laboratory of Road Traffic, Jilin University,Changchun 130022, Jilin, China;4. Shandong High-Speed Group Co.,Ltd.,Jinan 250014, Shandong, China) Abstract:As the existing optimal route planning algorithms do not fully consider the waiting time of vehicles with different movement types at signal intersections, no satisfactory optimal routes can be obtained. In order to solve this problem, an optimal route planning algorithm considering the movement type at signal intersections is proposed. In this algorithm, first, a waiting time model considering the movement type at signal intersections is esta-blished. Then, an improved forward star structure is constructed to optimize the representation and storage of the movement type and information in the road network. Moreover, an extended A* algorithm considering the movement type, namely CMTA* algorithm, is developed, and a case study is carried out. The results show that, as compared with the traditional algorithm and the CWTSI-SP algorithm considering the waiting time at intersections, CMTA* algorithm helps to obtain better routes with lower time cost. Key words:optimal route planning algorithm; intersection; movement type; waiting time; traffic engineering 收稿日期:2015- 07- 22 *基金项目:国家科技支撑计划项目(2014BAG03B03) Foundation item:Supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China(2014BAG03B03) 作者简介:周熙阳(1989-),男,博士生,主要从事智能交通运输系统研究.E-mail:xyzhou@vip.126.com †通信作者: 张伟(1978-),男,博士后,主要从事智能交通运输系统研究.E-mail:z_wei@126.com 文章编号:1000- 565X(2016)04- 0101- 08 中图分类号:U 491 doi:10.3969/j.issn.1000-565X.2016.04.015



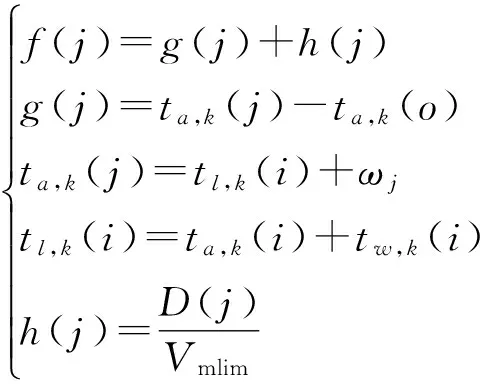
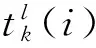


——国外课堂互动等待时间研究的现状与启示

