考虑直流功率调节次数限制的交直流系统动态无功优化*

李清　刘明波　赵文猛

(华南理工大学 电力学院， 广东 广州 510640)

考虑直流功率调节次数限制的交直流系统动态无功优化*

李清刘明波赵文猛

(华南理工大学 电力学院， 广东 广州 510640)

摘要：为避免直流功率的频繁调节，建立了考虑直流调节次数限制的交直流系统动态无功优化模型，并应用广义Benders分解方法求解.分解迭代中，将直流功率变量同整数变量一起划分到上层主问题中，这样下层问题能够分解为多个独立的单个时间段面的交直流优化子问题，同时采用一种紧凑的Benders割将子问题的优化信息传递到主问题中.在逐次线性逼近最优直流输电功率中，提出了一种动态调整直流功率变化步长的策略.最后以一个实际交直流互联大电网为例，验证了文中算法在限制直流功率调节次数方面的有效性和正确性，同时分析了不同最大调节次数限制取值对交直流动态无功优化结果的影响.

关键词：交直流系统；动态无功优化；广义Benders分解；逐次线性逼近

交直流互联电网中，相对于交流输电线路，直流线路传输功率具有更强的可控性，通过协调交直流并联线路的传输功率，能够有效降低系统的输电损耗[1- 2].考虑到互联电网一天中各区域负荷波动较大，若从单个时间断面考虑交直流互联电网无功优化问题，直流线路传输功率需要频繁调节，这不仅会降低设备的使用寿命，同时由于直流线路功率调整会导致系统有功潮流发生较大变化，不利于系统的稳定运行，因此从全天的角度来考虑计及直流调节次数限制的交直流动态无功优化问题更符合实际运行要求.

动态无功优化是一个多时段的非线性混合整数规划问题，如何处理变量的离散特性[3- 4]和高维特性[5- 6]一直是这类问题的研究难点，常见的计算方法包括动态规划法[7]、内点法[5- 6,8]和启发式算法[9- 12]等.其中文献[5- 6]在应用内点法求解时根据修正方程系数矩阵具有对角加边分块的结构特征，将高维线性方程组解耦为多个低维线性方程组.文献[8- 9]在处理离散变量时都将其松弛为连续变量，不同的是文献[8]中通过引入二次罚函数实现离散变量在优化中的逐次归整，而文献[9]中则根据连续优化结果建立一个整数二次规划模型获得离散归整结果.此外，文献[10]中结合遗传算法和内点法分别在处理离散变量和连续变量问题中的优势，将整数变量和连续变量分开进行优化，提出了一种有效解决动态无功优化问题的混合算法.在求解非线性混合整数规划问题中，广义Benders分解[13- 16]也是一种有效的方法.文献[15- 16]应用广义Benders分解将多时段的动态无功优化问题转化为上层整数规划问题和下层多时段耦合的非线性规划问题，经过反复迭代得到最优解.虽然文献[15- 16]中将离散变量和连续变量进行分层优化，但下层子问题是一个多时段耦合的问题，求解仍然比较困难.

文中在求解考虑直流调节次数限制的交直流系统动态无功优化时，为同时兼顾变量的离散特性和高维特性，考虑到相邻时段仅直流线路功率存在耦合的特性，在文献[15- 16]中介绍的广义Benders原理基础上，将参与时段间耦合的直流功率变量与整数变量一起划归到上层主问题中，这样下层问题能够解耦为各时段相互独立的交流系统无功优化子问题.分解迭代过程中采用一种紧凑的Benders割将子问题的优化信息传递到主问题中，同时为保证求解上层主问题得到的直流功率值在子问题中可行，迭代中通过动态调整直流功率的变化步长，应用逐次线性逼近法去获得最优的直流输电功率.

1考虑离散化直流输电调节约束的交直流系统动态无功优化模型

假设交直流系统共有Nb个交流节点、Ng台发电机、Nd条直流输电线路，选取系统全天有功损耗为目标函数.将全天等分为T个时间段，从而将各负荷母线有功和无功变化曲线分为T段，并认为各时间段中的负荷功率保持恒定，同时选择极小化各时间段的平衡机有功出力代替极小化系统的有功损耗，这样优化目标可以表示为

(1)

式中，PGs(t)为第t个时段下平衡机的有功出力.

图1为交直流系统及换流器接线示意图，其中Vi和θi为交流节点i处的电压幅值和相角，Pis和Qis为注入节点i的有功和无功功率，i=1,2,..,Nb;Vdk和Idk分别为换流器k侧直流电压和直流电流，Tdk和Xdk分别为换流变压器的变比和电抗，k=1,2,…,2Nd.

图1　换流站简化接线图

对于每个时段t，交直流系统需要满足的约束条件包括[17]：

a)纯交流节点的功率平衡方程：

(2)

式(2)中，Gij、Bij分别代表节点i和节点j之间的电导和电纳.

b)换流站交流节点的功率平衡方程：

(3)

式(3)中，φk(t)代表换流器k的功率因数角，当换流站在整流侧时spk=1，在逆变侧时spk=-1.

c)换流器的基本方程：

Vdk(t)-Tdk(t)Vk(t)cosθdk(t)+Idk(t)Xdk=0

(4)

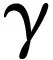
(5)

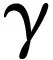
d)直流线路方程：

Vdr(t)-Vde(t)-Idr(t)Rdr=0

(6)

式(6)中：Vdr(t)、Vde(t)分别为整流测和逆变侧的直流电压；r,e=1,…，Nd；Rdr为直流线路电阻.

e) 变量上、下限值约束：

(7)

式(7)中变量的下标min和max分别表示下限和上限.优化中交流电压V、直流电压Vd和直流电流Id视为状态变量，机组无功出力QG、换流器控制角θd和换流变压器变比Td视为控制变量.

实际运行中，整流侧电压Vdr(t)保持为额定运行电压，因而直流线路电流的大小由所传输的直流功率Pdr(t)决定，即

(8)

由于计及了直流线路功率在一天内的调整次数限制，相邻时段间同一条直流线路传输的功率还需要满足以下约束条件：

(9)

式中：Pdr(t)为第r条直流线路在第t时段的功率；ΔPdr(t)表示第r条直流线路在t时段相对于第(t-1)时段的功率增减量；ur(t)∈{0,1}，是第r条直流线路在t时段的增/减状态，为0表示该直流线路在此时段维持与上一时段相同数值，为1表示此直流线路在上一时段基础上增加或减少，具体取决于ΔPdr(t)的数值；Crmax为第r条直流线路一天内允许的最大调节次数.

2基于广义Benders原理的分解计算

2.1主问题和子问题的分解及数学表达

为讨论方便，将式(1)-(9)描述的交直流动态无功优化模型简写为

(10)

s.t.

h(x1(t),x2(t),Pd(t))=0

(11)

{x1(t),x2(t)}∈X

(12)

{Pd(t),ΔPd(t),u(t)}∈Y

(13)

式中，x1=[θPGs]T代表无约束变量，x2=[VQG

VdTdθd]T代表有约束变量,X为式(7)所示的约束集合，Y为(8)-(9)的约束集合.

式(10)-(13)所描述的非线性混合整数规划问题中，相邻时段间仅直流功率变量存在耦合关系，因此文中在应用广义Benders原理时，将连续变量Pd(t)、ΔPd(t)与整数变量u(t)一起划分到上层主问题中，这样下层问题为T个直流功率分别给定下的交流系统无功优化子问题，此时各个子问题相互之间完全解耦.因而文中所考虑的交直流动态优化问题可以分解为两层优化进行.

下层优化问题为T个独立的非线性规划问题：

ξ(Pd(t))=minf(x1(t),x2(t),Pd(t))

(14)

s.t.

h(x1(t),x2(t),Pd(t))=0

(15)

{x1(t),x2(t)}∈X

(16)

上层优化问题为一个规模较小的混合整数规划问题：

(17)

s.t.

{Pd(t),ΔPd(t),u(t)}∈Y∩W

(18)

式(18)中集合W定义为

{Pd(t):∃(x1(t),x2(t))∈X}

(19)

s.t.

h(x1(t),x2(t),Pd(t))=0.

在下层优化问题中，直流功率为给定值，因此对每个子问题均需要增加如下等式约束：

(20)

(21)

(22)

这样上层优化问题可以表达为

(23)

s.t.

(24)

{Pd(t),ΔPd(t),u(t)}∈Y∩W

(25)

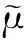
(26)

其中，

(27)

(28)

式中，ε为上下层目标函数值之间的间隙，ε0为预设的收敛精度.若式(26)满足则结束计算，否则将主问题求得的直流功率值传递到下层子问题中，待形成新的Benders割后增加到主问题约束集中，反复迭代直到满足条件(26).

2.2直流功率变化步长的动态调整策略

子问题反馈给上层主问题的Benders割中，系统有功损耗与直流线路功率间的关联被表示为线性形式，使得相邻两次分解迭代中主问题得到的直流功率可能会出现大幅振荡.由于直流功率调整会引起交流系统有功潮流较大的变化，这样会出现上层主问题优化得到的直流功率值在下层子问题中不可行的情况.为此，文中在主问题求解中对直流功率的变化加以一定步长约束，通过逐次逼近得到最终直流送电曲线.

(29)

(30)

(31)

(32)

3算法流程

由式(7)可以推导出在广义Benders分解框架下，计及直流功率调节次数限制的动态交直流互联大电网无功优化算法的完整计算步骤如下：

步骤1初始化.输入系统参数；设置各条直流线路功率的预设固定步长和一天内最大调节次数，以及收敛间隙精度值，置迭代次数k=1.

步骤2求解下层非线性子问题.根据上层主问题优化结果中的直流功率，求解下层各时间断面下的交直流无功优化子问题，得到各时段平衡机的有功出力和式(20)对应的拉格朗日乘子.

步骤3根据下层子问题的优化解形成式(22)所示的紧凑Benders割，并增添到主问题约束集合中.

步骤4求解上层混合整数规划问题.根据上一次主问题优化结果中ur(t)和Pdr(t)的值确定本次迭代中Pdr(t)的变化步长后，求解式(23)-(25)所示主问题，得到直流最优调节状态以及各直流线路的送电曲线.

步骤5计算上下两层问题目标函数的间隙ε，判断是否满足精度要求.若满足，则结束迭代，输出最终直流输电曲线和系统有功网损；否则，置k=k+1，转入步骤2.

4算例分析

4.1系统规模和参数

选取一实际交直流互联电网2013年4月某一日的等值主网架作为研究对象验证文中方法的有效性，优化考虑的时段尺度为00:00～24:00，以15min为一个断面间隔，这样全天可以分为96个时间断面.其中该等值系统的简化结构图如2所示，包含749个节点、144台发电机组、4条直流输电线路和662条变压器支路，在第6～41时间断面下交流线路数为351条，其它断面下线路条数为350条.4条直流输电系统的基本运行参数如表1所示.

图2　一个实际交直流互联电网简化接线图

Fig.2SimplifiedconnectiondiagramofanAC/DCinterconnectedpowersystem

表1直流输电系统基本运行参数

Table1BasicoperatingparametersoftheDCtransmissionsystem

直流系统额定功/MW整流侧额定电压/kV天广直流1800500高肇直流3000500兴安直流3000500云广直流5000800

设定直流线路传输的最大功率为额定功率值，最小功率为额定功率值的10%.此外考虑到实际电网运行中对电压幅值的安全约束要求，对不同电压等级设置表2所示的上、下限值.

表2　节点电压上、下限值

应用广义Benders分解迭代时，每条直流线路的预设步长为其额定功率值的1%，收敛间隙值ε0设为0.1%.第1次迭代时，对于00:00～08:00的时间断面，设各直流功率的初始值为其额定功率值的30%，对于08:00～24:00的时间断面，为其额定功率值的75%.文中所有算法均在GAMS[18]框架下编程实现，其中求解非线性子问题时调用CONOPT解法器，求解混合线性整数规划主问题时调用CPLEX解法器，计算机硬件平台为主频3.40GHz的英特尔至强双核处理器，内存为32GB.

4.2考虑调节次数限制下的直流输电曲线

设定每条直流线路的传输功率在一天内最大调节次数Crmax为24，应用文中算法求解计及直流功率调节次数限制的动态交直流无功优化，分解迭代过程中上下层目标值间隙的变化如图3所示.

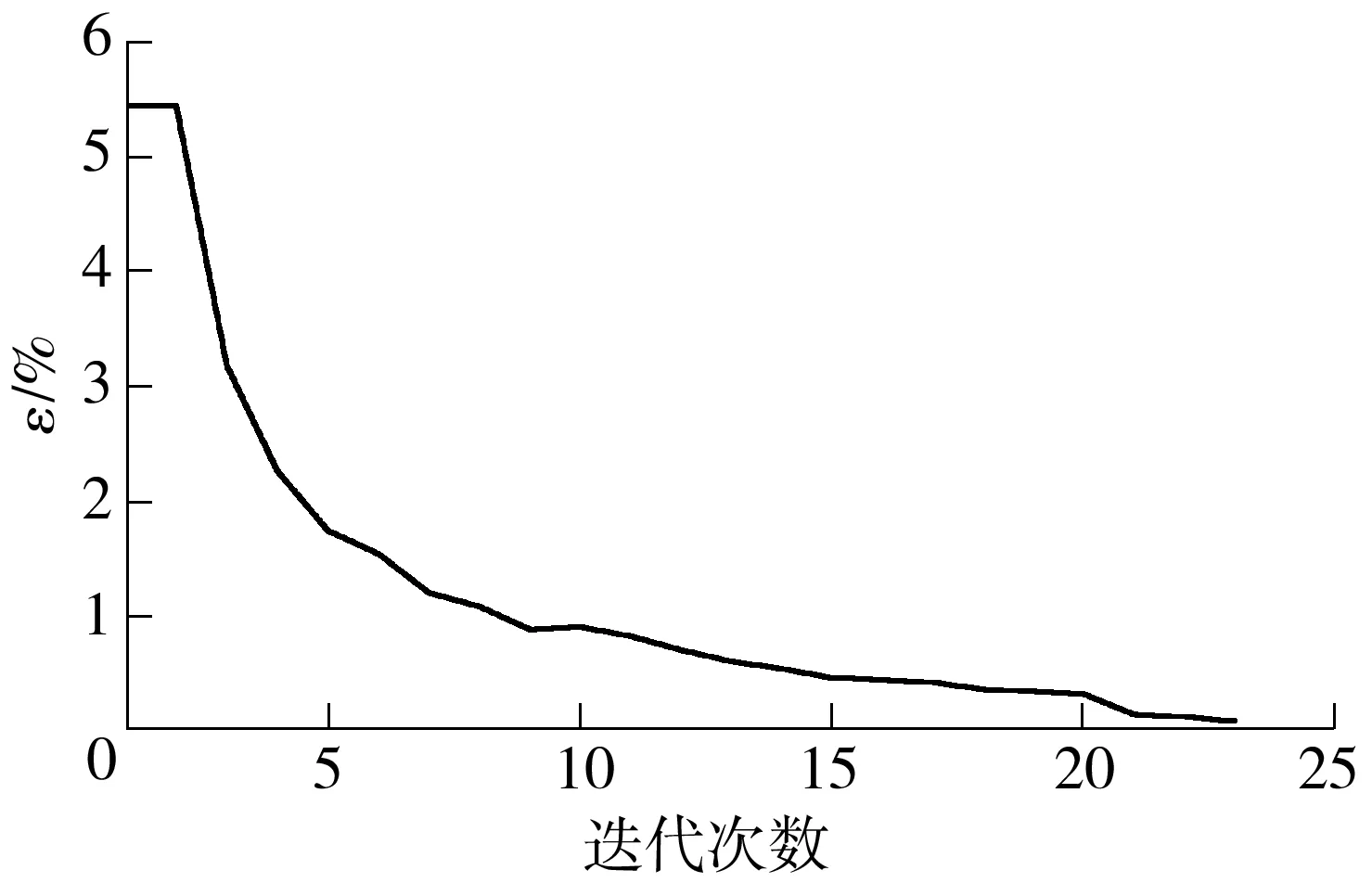
图3　迭代中上、下层目标值间隙的变化过程

Fig.3Changeofgapbetweenthemasterproblemandsubproblemduringiteration

当k=23时，上、下两层的目标函数值分别为20 436.90MW和20 453.10MW，此时两者间隙为0.08%，满足收敛要求.整个运算过程耗时1 303.48s，其中主问题计算耗时43.95s，子问题计算耗时1 259.53s.

优化前后各个时间断面下，系统有功损耗及节点电压与其额定电压的平均偏差变化情况分别如图4、5所示.在图4中，第19个时间断面系统降低的有功损耗为26.05MW，第93个时间断面系统降低的损耗为112.45MW，这两个断面分别为一天中降损值最小和最大的两个时段.与优化前相比，虽然优化后系统一天内减少的有功损耗为1 564.08MW·h，但各个时段下节点电压与其额定电压的平均偏差值均有一定增加，因此实际运行中以全网有功损耗最小为目标优化调整时也应兼顾节点电压与其额定电压的平均偏差值这个目标.

优化中本文也计算了未考虑直流调节次数限制下的96个交直流静态无功优化的情况，与优化前相比，

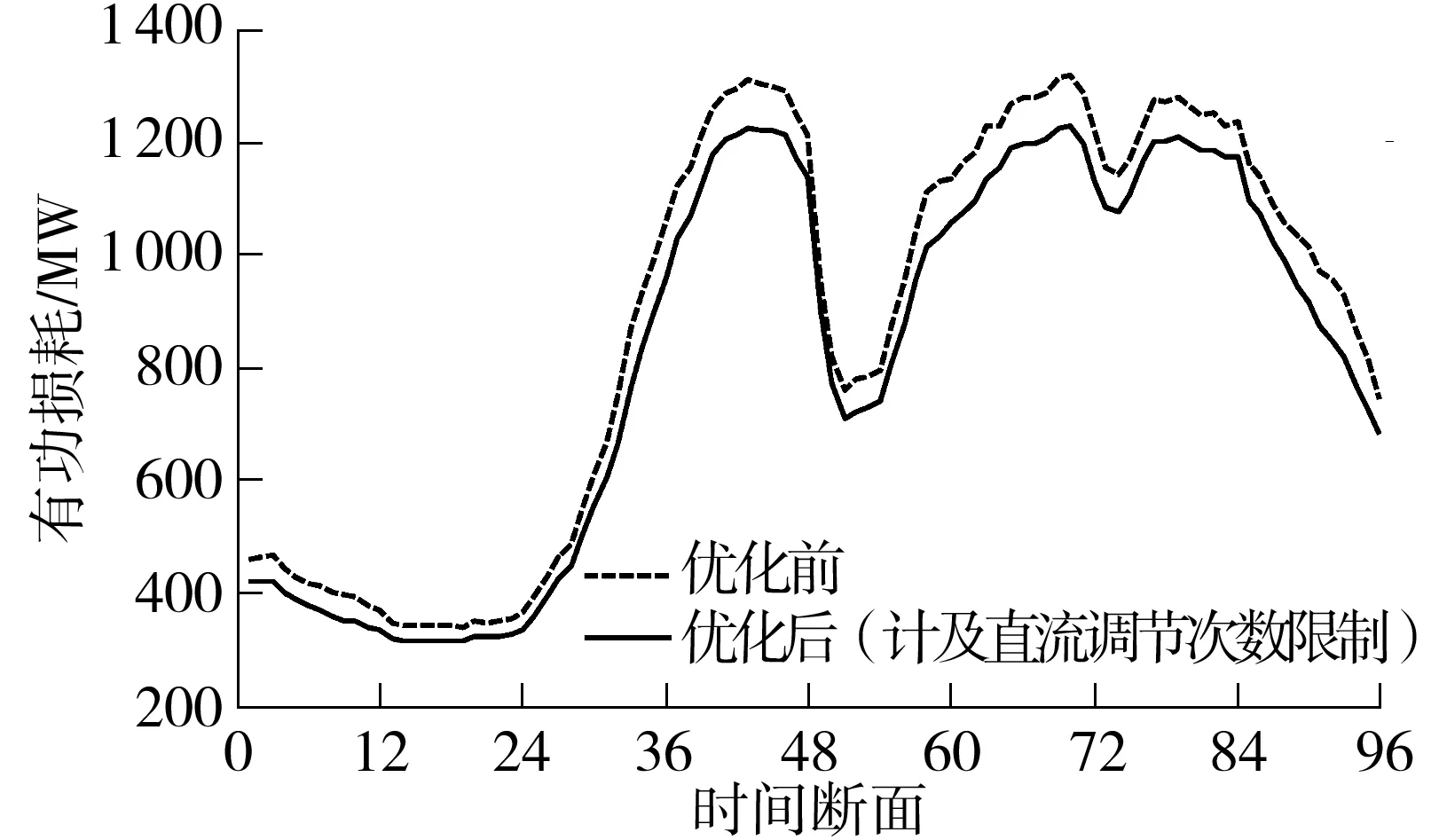
图4　优化前后系统有功损耗变化曲线

Fig.4Changcurvesofactivepowerlossbeforeandafteroptimization

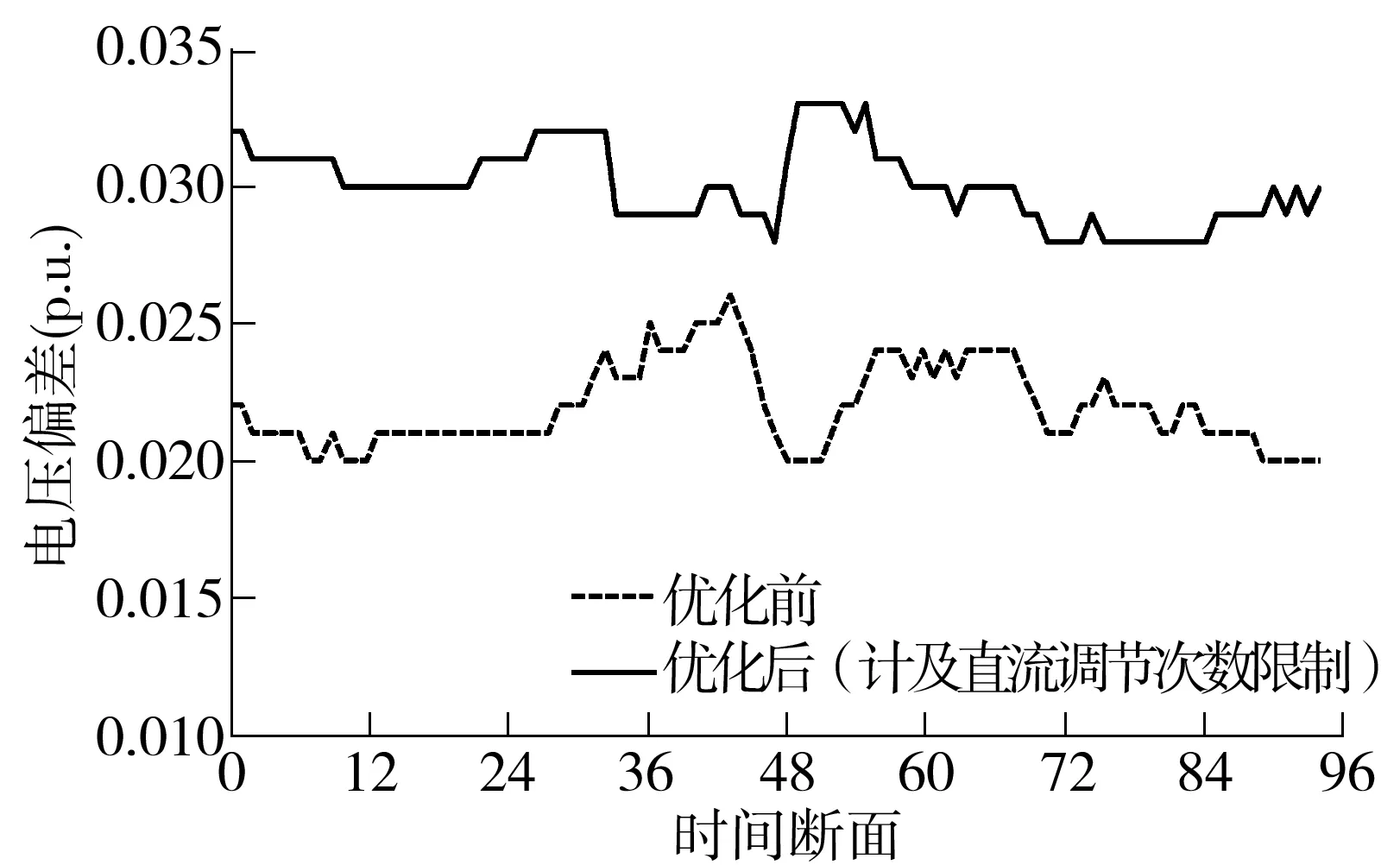
图5　优化前后系统电压偏差变化曲线

Fig.5Changcurvesofvoltagedeviationbeforeandafteroptimization

优化后系统一天内减少的有功损耗为1 581.23MW·h.虽然未考虑直流调节次数时系统在大部分时间断面内的有功损耗均小于考虑直流调节次数时的有功损耗，但两者间有功损耗的差值已很小，如图6中柱状图所示，尤其是前者优化得到的直流送电曲线波动较为频繁，而后者能够保证每条直流线路功率的调节次数不超过最大调节次数限制，4条直流线路的输电曲线如图7所示.

图6　考虑和不考虑直流调节次数时系统有功损耗的差值

Fig.6DifferenceofactivepowerlossescorrespondingtoconsideringDCpowerregulationlimitsandnotrespectively

未考虑直流功率调节次数限制时，由于相邻断面间的直流功率不存在耦合约束，导致优化得到的直流输电功率在进入下个时段时都需要调整，如图7中实点线所示.而引入直流功率最大调节次数限制后，由于各个时段之间的直流输电功率存在耦合使得这些时段下的交直流无功优化成为一个整体，优化得到的直流输电功率在一天内的调整次数均在设定的最大次数内，如图7中实线所示.

为比较这两种情况下直流功率的偏差程度，验证文中方法的正确性，统计每条直流在考虑直流调节次数时得到的最优送电曲线与未考虑直流调节次数时的平均偏差值，并用gap代表其占该直流线路额定功率值的比重：

(33)

图7　优化前后的直流线路全天送电计划曲线

Fig.7DailyschedulingcurvesofDCtransmissionpowerbeforeandafteroptimization

各直流输电线路的gap值如表3所示，可以看到，计及直流调节次数和未计及直流调节次数这两种情况下，每条直流线路送电功率的平均偏差值占其额定功率值的比重都很小.同时对比图7中实点线和实线的变化趋势也可以看到，两种情况下直流输电功率调整方向都是一致的，各个时段下两者的直流功率也比较接近，这也反映出文中所考虑的交直流动态无功优化在限制直流输电功率调节次数方面起到了较好的效果.

表3　不同直流输电系统的gap值

4.3不同调节次数限制下系统有功损耗结果分析

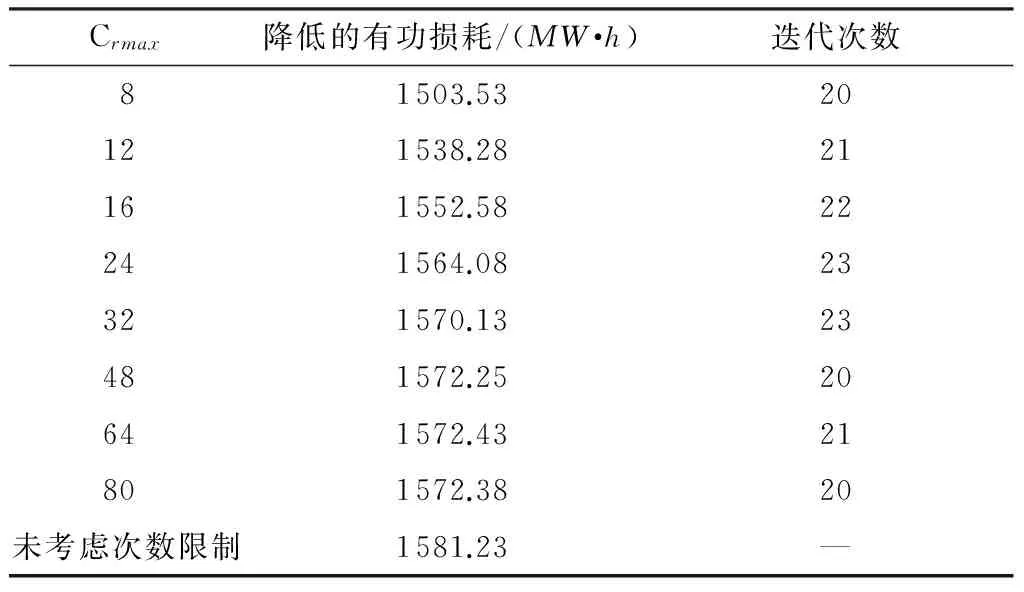
为分析不同直流最大调节次数限制取值对交直流动态无功优化结果的影响，表4列出了优化过程中设置不同的最大调节次数时系统一天降低的有功损耗.

由表4中最大调节次数与降低的有功损耗间的关系可以看到，随着直流线路调节次数限制值的放松，系统降低的有功损耗呈现出增大的趋势.从Crmax为8时开始，Crmax为12、16、24和32时系统的有功损耗在前者基础上分别减小了34.75、14.30、11.50和6.05MW·h，而当继续增大Crmax时系统降低的有功损耗已较小，说明此时放松调节次数限制对网损降低的作用已不再明显.

表4系统降低的有功损耗随不同Crmax取值的变化情况

Table4ChangeofactivepowerlosscorrespondingtoDifferentCrmax

Crmax降低的有功损耗/(MW·h)迭代次数81503.5320121538.2821161552.5822241564.0823321570.1323481572.2520641572.4321801572.3820未考虑次数限制1581.23—

5结语

为降低子问题的求解难度，文中在应用广义Benders原理求解交直流动态无功优化时，将参与各时段耦合的直流功率变量和整数变量一起划分到上层主问题中，提出了一种计及直流调节次数限制的交直流动态无功优化的新策略.为保证迭代分解中主问题优化得到直流功率值在子问题中可行，对直流功率变化设置一定的步长后，迭代中动态调整直流功率变化步长，通过对一个实际交直流互联电网的验证分析说明文中方法能够有效解决考虑调节次数限制后的交直流动态无功优化问题，对比优化前后系统有功损耗变化曲线，能够看到通过调整直流功率能够有效降低系统网损.另外，从不同最大动作次数限制取值对交直流动态无功优化结果的影响可以看到但减少直流调节次数是以系统有功损耗增加为代价，因此实际调度运行中应协调好两者之间的关系.

参考文献：

[1]邱有强,刘洪涛,邹江,等.南方电网直流输电损耗分析及基于降损的交直流潮流优化探讨 [J].南方电网技术,2008,2(4):83- 107.

QIUYou-qiang,LIUHong-tao,ZOUJiang,etal.AnalysisonHVDCtransmissionlossandoptimizationofAC/DCpowerflowforreducingtransmissionlossinCSG[J].SouthernPowerSystemTechnology,2008,2(4):83- 107.

[2]刘恺,陈亦平,张昆,等.大型交直流并联输电网网损优化理论及其在南方电网中的实现 [J].中国电机工程学报,2014,34(1):130- 137.

LIUKai,CHENYi-ping,ZHANGKun,etal.TheoreticalstudyoflossminimizationforalargeAC/DCpowersystemanditsimplementationinCSGsystems[J].Procee-dingsoftheCSEE,2014,34(1):130- 137.

[3]林济铿,石伟钊,武乃虎,等.计及离散变量基于互补约束全光滑牛顿法的无功优化 [J].中国电机工程学报,2012,32(1):93- 100.

LINJi-keng,SHIWei-zhao,WUNai-hu,etal.ReactivepoweroptimizationwithdiscretevariablesbasedoncomplementarityconstraintssmoothNewtonmethod[J].ProceedingsoftheCSEE,2012,32(1):93- 100.

[4]李志刚,吴文传,张伯明,等.一种基于高斯罚函数的大规模无功优化离散变量处理方法 [J].中国电机工程学报,2013,33(4):68- 76.

LIZhi-gang,WUWen-chuan,ZHANGBo-ming,etal.Alarge-scalereactivepoweroptimizationmethodbasedonGaussianpenaltyfunctionwithdiscretecontrolvariables[J].ProceedingsoftheCSEE,2013,33(4):68- 76.

[5]赖永生,刘明波.电力系统动态无功优化问题的快速解耦算法 [J].中国电机工程学报,2008,28(7):32- 39.LAIYong-sheng,LIUMing-bo.Fastdecompositionalgorithmforsolutionofdynamicreactivepoweroptimizationprobleminpowersystems[J].ProceedingsoftheCSEE,2008,28(7):32- 39.

[6]缪楠林,刘明波,赵维兴.电力系统动态无功优化并行算法及其实现 [J].电工技术学报,2009,24(2):150- 157.

MIAONan-lin,LIUMing-bo,ZHAOWei-xing.Parallelalgorithmofdynamicreactivepoweroptimizationanditsimplementation[J].TransactionsofChinaElectrotechnicalSociety,2009,24(2):150- 157.

[7]LIANGRH,CHENGCK.DispatchofmaintransformerULTCandcapacitorsinadistributionsystem[J].IEEETransactionsonPowerDelivery,2001,16(4):625- 630.

[8]刘明波,朱春明,钱康龄,等.计及控制设备动作次数限制的动态无功优化算法 [J].中国电机工程学报,2004,24(3):39- 45.

LIUMing-bo,ZHUChun-ming,QIANGKang-ling,etal.Dynamicreactive-poweroptimizationalgorithmincorporatingactionnumberconstraintsofcontroldevices[J].ProceedingsoftheCSEE,2004,24(3):39- 45.

[9]丁涛,郭庆来,柏瑞,等.松弛MPEC和MIQP的启发-校正两阶段动态无功优化算法 [J].中国电机工程学报,2014,34(13):2100- 2107.

DINGTao,GUOQing-lai,BORui,etal.Two-stageheuristic-correctionfordynamicreactivepoweroptimizationbasedonrelaxation-MPECandMIQP[J].ProceedingsoftheCSEE,2014,34(13):2100- 2107.

[10]颜伟,田甜,张海兵,等.考虑相邻时段投切次数限制的动态无功优化启发式策略 [J].电力系统自动化,2009,32(10):71- 75.

YANWei,TIANTian,ZHANGHai-bing,etal.Heuristicstrategyfordynamicreactiveoptimizationincorporatingactiontimeconstraintsbetweenadjacenttimeintervals[J].AutomationofElectricPowerSystems,2008,32(10):71- 75.

[11]杨素琴,韩念杭.计及调节次数的变电站动态电压无功优化控制的研究 [J].电力系统保护与控制,2010,38(24):131- 136.

YANGSu-qin,HANNian-hang.Dynamicreactivepower/voltageoptimizationcontrolofsubstationconsideringthenumberofswitchingoperations[J].PowerSystemProtectionandControl,2010,38(24):131- 136.

[12]董洁,赵凤展,杨仁刚.采用启发式策略的动态无功优化混合算法研究 [J].电力系统保护与控制,2011,39(5):35- 40.

DONGJie,ZHAOFeng-zhan,YANGRen-gang.Studyondynamicreactivepoweroptimizationhybridalgorithmusingheuristicstrategy[J].PowerSystemProtectionandControl,2011,39(5):35- 40.

[13]GEROMELJC,BELLONIMR.Nonlinearprogramswithcomplicatingvariables:theoreticalanalysisandnumericalexperience[J].IEEETransactionsonSystems,ManandCybernetics,1986,16(2):231- 239.

[14]SIFUENTESWS,VARGASA.HydrothermalschedulingusingBendersdecomposition:acceleratingtechniques[J].IEEETransactionsonPowerSystems,2007,22(3):1351- 1359.

[15]ALGUACILN,CONEJOAJ.MultiperiodoptimalpowerflowusingBendersdecomposition[J].IEEETransactionsonPowerSystems,2000,15(1):196- 201.

[16]RABIEEA,PARNIANIM.Voltagesecurityconstrainedmulti-periodoptimalreactivepowerflowusingbendersandoptimalityconditiondecompositions[J].IEEETransactionsonPowerSystems,2013,28(2):696- 708.

[17]王锡凡,方万良,杜正春.现代电力系统分析 [M].北京:科学出版社,2003:186- 189.

[18]GAMSDevelopmentCorporation.GAMS,theSolvers’Manual[EB/OL].[2015- 06- 01].http:∥www.gams.com/solvers/allsolvers.pdf.

DynamicReactivePowerOptimizationConsideringDCPower
RegulationLimitinAC/DCPowerSystems

LI QingLIU Ming-boZHAO Wen-meng

(SchoolofElectricPower,SouthChinaUniversityofTechnology,Guangzhou510640,Guangdong,China)

Abstract:In order to avoid frequent power regulation of DC transmission lines, a dynamic reactive power optimization model of AC/DC power systems, which takes into consideration the DC power regulation limits, is established and then solved by using the generalized Benders decomposition. In the decomposition process, the power variables of DC transmission lines are divided in the master problem together with integer variables, so that the sub-problem can be transformed into a set of independent AC/DC optimization problems in single time section. At the same time, a tightened Benders cut is used to transfer the sub-problem information into the master problem. Moreover, in order to obtain the optimal power of DC transmission lines in a successive linear way, a dynamic step adjustment strategy is proposed. The results on a real large-scale AC/DC interconnection power grid demonstrate the correctness and effectiveness of the proposed method in restricting the regulation times of DC power. Finally, the effect of maximum regulation limit on the dynamic reactivepower optimization results is analyzed.

Key words:AC/DC power system; dynamic reactive power optimization; generalized Benders decomposition; successive linear approximation

收稿日期：2015- 06- 11

*基金项目：国家高技术研究发展计划(863计划)项目(2012AA050209)；国家自然科学基金资助项目(51277078)

Foundation items: Supported by the National High Technology Research and Development of China(863 Program) (2012AA050209)and the National Natural Science Foundation of China(51277078)

作者简介：李清(1989-)，男，博士生，主要从事电力系统优化与控制研究.E-mail：liqing6291@163.com.

文章编号：1000- 565X(2016)04- 0055- 08

中图分类号：TM 712

doi：10.3969/j.issn.1000-565X.2016.04.009