基于最小熵解卷积和能量算子的滚动轴承故障诊断方法
柳玉昕,石 岩,王美俊,田松峰
(1.东北石油大学 电气信息工程学院,黑龙江 大庆 163318;2.燕山大学 经济管理学院,河北 秦皇岛 066004;3.华北电力大学 能源动力与机械工程学院,河北 保定 071003)
基于最小熵解卷积和能量算子的滚动轴承故障诊断方法
柳玉昕1,石岩2,王美俊3,田松峰3
(1.东北石油大学 电气信息工程学院,黑龙江 大庆163318;2.燕山大学 经济管理学院,河北 秦皇岛066004;3.华北电力大学 能源动力与机械工程学院,河北 保定071003)
摘要:针对滚动轴承故障识别困难这一问题,提出了基于最小熵解卷积和能量算子的诊断方法。首先利用最小熵解卷积算法对原始振动信号进行预处理,削弱冗余噪声成分的干扰,增强故障特征,继而计算解卷积信号的Teager能量算子输出,并对所得的瞬时能量信号做频谱分析,最终通过分析能量谱中的频率成分实现故障类型的准确判定。实测信号分析结果表明,基于最小熵解卷积和能量算子的诊断方法能够有效提取轴承故障信号中的微弱特征信息,具有一定工程应用价值。
关键词:滚动轴承;故障诊断;最小熵解卷积;Teager能量算子
0引言
作为风力发电机、鼓风机、电动机等电力设备上的重要组成部件,滚动轴承的运行状态直接影响设备的整体性能及工作效率,如果能在轴承早期失效阶段实现故障的准确判别并及时排除隐患,对于确保设备安全稳定运行,避免出现连锁事故及经济损失具有重要意义,因此探寻行之有效的滚动轴承故障诊断方法一直以来都是学术界和工程界的研究热点[1-2]。
近些年,针对轴承故障检测这一问题,相关学者进行了深入研究,提出了诸多具有针对性的诊断策略,如罗忠辉[3]结合离散小波变换和经验模态分解来诊断电机轴承故障,效果较为理想,但离散小波变换实质上是对信号频带的一种格型二进制剖分,这种信号分解方式很容易造成故障相关成分能量的泄露。Wang等[4]则利用约束独立成分分析来处理轴承加速疲劳试验信号,该方法具有可借鉴之处,但在故障信号分离过程中需要构造一个准确的参考信号,参考信号构建的不合理将直接导致特征提取失败;在文献[5]中,作者提出了融合可调品质因子小波变换和集合经验模态分解的滚动轴承微弱特征提取方法,但可调品质因子小波的参数设定值对最终分析结果存在较大影响,很难同时确定合理的品质因子及冗余因子。为提取轴承早期失效信号中的特征信息,唐贵基等[6]提出了自适应最大相关峭度解卷积方法,但是利用粒子群来优化解卷积算法时,仍需要根据一定的先验知识来设定搜寻过程中的控制参数。
针对上述方法存在的不足,为了快速、准确、有效地提取出轴承早期故障阶段的微弱特征信息,本文提出一种基于最小熵解卷积和能量算子的故障甄别方法,并利用试验平台上拾取的轴承内、外圈故障振动信号对所述方法进行验证。
1最小熵解卷积
设通过传感器拾取的实测信号由下式表示为[7-8]:
y(n)=h(n)·x(n)+e(n)
(1)
其中,x(n)为原始激励信号,e(n)为噪声,h(n)为系统频响函数,y(n)是实测信号。
最小熵解卷积(MinimumEntropyDeconvolution,MED)可通过构造逆滤波器ω(n),从实测信号y(n)中恢复得到原始激励信号x(n),即:
x(n)=ω(n)·y(n)
(2)
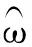
(3)

(4)
由式(2)可知:
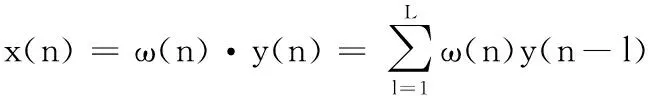
(5)
其中,L为逆滤波器ω(n)的长度。
对上式两侧同时求导,整理后可得:

(6)
结合式(4)和式(6),进一步计算得出:
(7)
上式可写成如下矩阵形式:
b=Aω
(8)
其中,A为实测信号y(n)的Toeplitz自相关矩阵,b=(b(l))T,而b(l)的表达式如下:
(9)
(10)
通过式(8)可迭代计算出逆滤波器矩阵ω=A-1b。
最小熵迭代计算流程可简要归纳如下:
(1)将ω(0)中的所有元素初始化为1;
(2)迭代计算x(n)=ω(n)(i-1)·y(n);

(4)计算ω(i)=A-1b(i);

2Teager能量算子
对一个时间信号x(t)做Teager能量算子运算后,可得到其瞬时能量信号φ{x(t)},数学表达式为[9]:

(11)
传统意义上的信号能量定义为信号幅值的平方,只代表动能或势能,而信号x(t)经能量算子运算后得到瞬时能量信号φ{x(t)},其本质为振动瞬时幅值和瞬时频率二者的平方之积,同时包含了动能和势能,是信号瞬时总能量的一种表述[10]。由于瞬态冲击信号通常振动幅值变化剧烈,振动频率较高,因此相对于传统的信号能量定义,能量算子能更为有效地突出冲击成分的瞬态特征。
3故障诊断流程
滚动轴承故障初期,由于存在运行环境噪声干扰及振动传递路径衰减等不利因素的影响,因此特征信息较弱,故障识别相对困难。MED方法可通过迭代过程构造出合理的滤波器反作用于信号的传递路径,恢复得到原始激励信号。轴承局部损伤信号通常蕴含周期性冲击成分,将MED方法作为一种预处理手段,对原始信号进行降噪处理,可减少无关成分的干扰,挖掘出信号中被噪声掩埋的连续脉冲,更有利于后续的分析过程。能量算子则可以快速准确的追踪信号总能量的变化,增强信号的瞬态特征,并具有响应迅速、计算简单等优点,适合作为后续处理技术来检测信号中的冲击脉冲成分。鉴于上述分析,本文将MED与能量算子相结合来处理滚动轴承故障信号,有望取得满意的分析效果,基于最小熵解卷积和能量算子的诊断方法的具体流程如下:
(1)利用MED算法对原始信号进行降噪处理。
(2)计算解卷积信号的Teager能量算子输出,得到解卷积信号的瞬时能量信号。
(3)为分析瞬时能量信号的周期性质,对其做进一步傅立叶变换,得到相应的能量谱。
(4)对比分析能量谱中幅值突出的频率成分及轴承理论故障特征频率,最终判定故障类型。
4试验信号分析
通过实测信号来验证所述方法的有效性,滚动轴承为6205型深沟球轴承,利用电火花加工技术在试验台轴承内、外圈分别制造一个直径约为0.18mm的微小凹痕来模拟轴承故障。试验过程中,利用安置在轴承座上方的压电加速度传感器采集竖直方向的振动信号,试验平台及传感器安装位置如图1所示,其中采样频率为12000Hz,采集点数8192点,传动轴转速1797r/min。根据轴承结构参数计算得到的特征频率如表1所示[11]。

图1 故障试验台

型号保持架fc内圈fi外圈fo滚动体fe620511.93162.19107.26141.17
实测信号的波形及谱图如图2所示,由于轴承损伤程度较轻,因此振动信号时域波形中周期性冲击特征不明显,频谱中没有出现明显的共振频带,低频段未发现故障相关成分。对时域信号做进一步包络谱分析,结果如图3所示,虽然谱图中能够找到内圈故障特征频率fi及其倍频成分2fi,但存在较多幅值较大的干扰谱峰,特征频率谱线成分不够突出,影响轴承运行状态的准确判定。
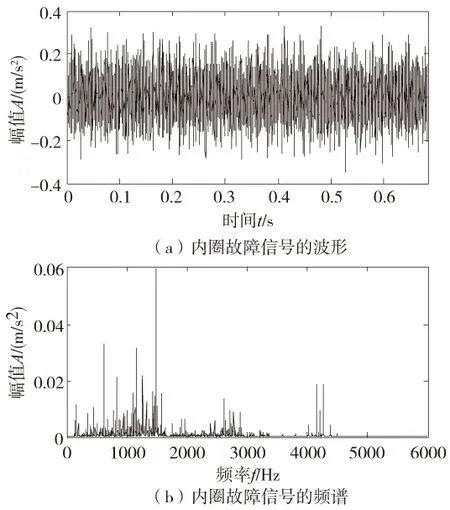
图2 内圈故障信号的波形及频谱
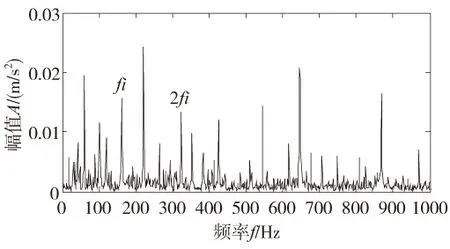
图3 内圈故障信号的包络谱
下面运用基于最小熵解卷积和能量算子的诊断方法对上述信号进行处理。图4a为原信号经MED处理后的结果,通过对比可以发现,原信号经过解卷积运算后,噪声干扰成分得到了良好的抑制,与轴承局部损伤有关的周期性冲击成分被有效挖掘出来。计算所得解卷积信号的瞬时能量波形,并做进一步频谱分析,结果如图4b所示。从所得的能量谱中,我们可以找到幅值十分明显的内圈故障特征频率及其各阶倍频成分fi~6fi,由此可以很容易断定轴承内圈存在局部缺陷,分析结果与实际情况完全一致。
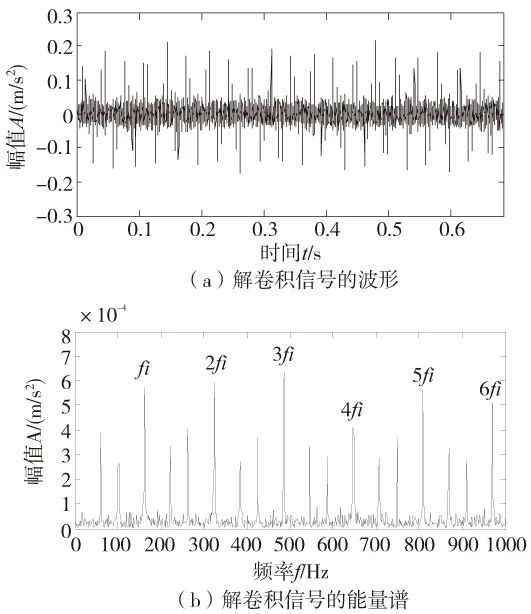
图4 本文方法的内圈故障信号分解结果
外圈故障信号的时域波形及谱图如图5所示,相比于内圈故障信号,该信号波形中冲击成分比重有所增加,但仅通过观察波形仍无法甄别轴承进行状态。图5b所示频谱中,信号的主导频率成分集中在2500Hz~5500Hz范围内,在低频段也未发现故障相关频率成分。该信号的包络谱分析结果如图6所示,虽然谱图中存在与外圈缺陷相对应的频率成分,但特征频率的倍频成分峰值不够明显,故障特征成分的连续性欠佳,分析效果存在很大的提升空间。
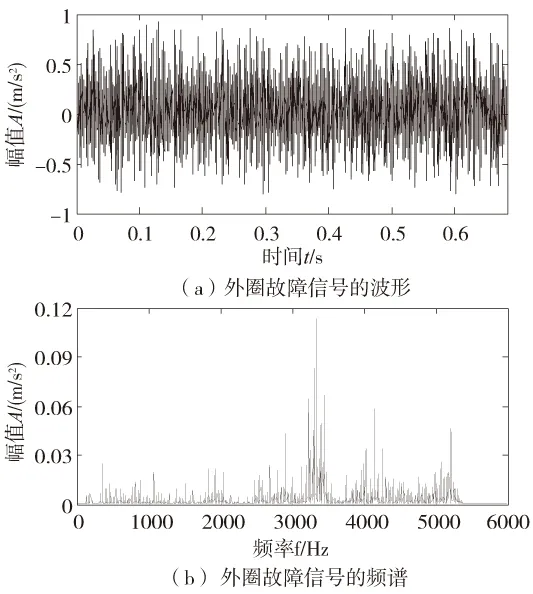
图5 外圈故障信号的波形及频谱
利用本文所述方法对外圈故障信号进行分析,结果如图7所示。同未经处理的原始信号相比,解卷积信号中周期性冲击特征更为明显,噪声干扰得到了一定抑制。所得能量谱中,外圈故障特征频率fo及相应倍频成分处谱线幅值均十分突出,而且倍频阶次连续,高达9阶。通过图6与图7b分析结果的对比可发现,本文阐述的方法能够更为直观明朗地表征出轴承故障相关成分。
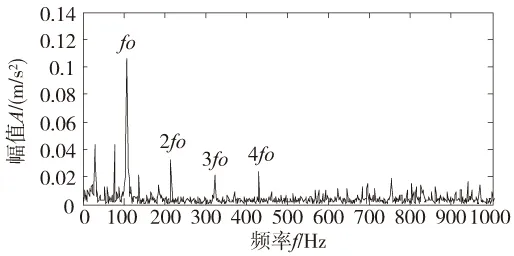
图6 外圈故障信号的包络谱

图7 本文方法的外圈故障信号分解结果
5结束语
针对滚动轴承故障识别问题,本文提出一种基于最小熵解卷积和能量算子相结合的诊断方法,实测信号分析结果表明,将两种方法相互结合,能够有效发挥二者的优势,做到优势互补。利用所述方法对拾取的故障信号进行处理,能够从信噪比较低的原始信号中顺利挖掘出隐含的故障特征信息,给出准确、可靠的诊断结果,并且与传统的频谱分析,包络谱分析方法相比,本文方法的分析效果更佳,优势明显,从而可以为设备维修和生产计划安排争取足够的缓冲时间,对于实际工程应用来说具有一定意义。
[参考文献]
[1] 安国庆,秦程,郭立炜,等.峭度滤波器用于电机轴承早期故障特征提取[J].电机与控制学报,2014,18(6):55-60.
[2] 唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报,2015,49(5):73-81.
[3] 罗忠辉,薛晓宁,王筱珍,等.小波变换及经验模式分解方法在电机轴承早期故障诊断中的应用[J].中国电机工程学报,2005,25(14):125-129.
[4] Wang Z Y,Chen J,Dong G M, et al.Constrained independent component analysis and its application to machine fault diagnosis[J].Mechanical Systems and Signal Processing,2011,25(7):2501-2512.
[5] Wang H C,Chen J,Dong G M.Feature Extraction of Rolling Bearing’s Early Weak Fault Based on EEMD and Tunable Q-factor Wavelet Transform[J].Mechanical Systems and Signal Processing,2014,48(1-2):103-119.
[6] 唐贵基,王晓龙.自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].中国电机工程学报,2015,35(6):1436-1444.
[7] 王宏超,陈进,董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报,2013,49(1):88-94.
[8] WIGGINS R A.Minimum entropy deconvolution,geophys[J].Exploration,1978,16:21-35.
[9] 唐贵基,王晓龙.基于EEMD降噪和1.5维能量谱的滚动轴承故障诊断研究[J].振动与冲击,2014,33(1):6-10.
[10] 王天金,冯志鹏,郝如江,等.基于Teager能量算子的滚动轴承故障诊断研究[J].振动与冲击,2012,31(2):1-5.
[11] Wang Y, Xu G H, Liang L,et al.Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis[J].Mechanical Systems and Signal Processing,2015,54-55:259-276.
(编辑赵蓉)
AMethodofFaultDiagnosisforRollingBearingBasedonMinimumEntropyDeconvolutionandEnergyOperator
LIUYu-xin1,SHIYan2,WANGMei-jun3,TIANSong-feng3
(1.DepartmentofElectricalInformationEngineering,NortheastPetroleumUniversity,DaqingHeilongjiang163318,China;2.SchoolofEconomicsandManagement,YanshanUniversity,QinhuangdaoHebei066004,China)
Abstract:To overcome the difficulty of fault diagnosis for rolling bearing,a diagnosis method based on minimum entropy deconvolution and Teager energy operator was proposed.Firstly,the original fault signal was preprocessed using the minimum entropy deconvolution algorithm, the interference of the redundant noise component could be weakened and the fault characteristic could become more obvious.Then the output of the Teager energy operator of the deconvolution signal was calculated,and the frequency spectrum analysis was performed on the obtained instantaneous energy signal.Finally,the fault type could be judged by analyzing the frequency components in the energy spectrum.The analysis results of the measured signal showed that,the method based on minimum entropy deconvolution and Teager energy operator could effectively extract the weak characteristic information immersed in the fault signal of the bearing,and has a certain value for engineering application.
Key words:rolling bearing;fault diagnosis;kurtosis;minimum entropy deconvolution;Teager energy operator
文章编号:1001-2265(2016)06-0114-04
DOI:10.13462/j.cnki.mmtamt.2016.06.030
收稿日期:2015-12-24;修回日期:2016-01-04
作者简介:柳玉昕(1987—),男,黑龙江绥化人,东北石油大学硕士研究生,研究方向为数值模拟与故障诊断,(E-mail)478074576@qq.com。
中图分类号:TH166;TG506
文献标识码:A

