双转台五轴联动数控机床轮廓误差控制方法*

庄丙远，赵国勇，翟静涛，侯春宏

(山东理工大学 机械工程学院，山东 淄博　255049)

双转台五轴联动数控机床轮廓误差控制方法*

庄丙远，赵国勇，翟静涛，侯春宏

(山东理工大学 机械工程学院，山东 淄博255049)

摘要：五轴数控加工中，机床几何精度、动态特性不匹配等因素引起的各种误差最终会表现为零件的轮廓误差，所以控制和补偿轮廓误差具有重要意义。以双转台五轴联动数控机床为对象，采用D-H法建立了数控机床运动学模型。运用运动学正解模型，揭示了刀心位置轮廓误差和刀轴方向轮廓误差的产生规律，为轮廓误差补偿控制提供了理论依据。在此基础上设计了一种轮廓误差补偿控制方法。仿真实验证明该控制方法能有效减小轮廓误差。

关键词：运动学模型；刀心位置轮廓误差；刀轴方向轮廓误差；误差补偿

0引言

五轴联动数控机床可以同时调整刀心位置和刀轴方向，广泛用于复杂曲面零件加工。在加工过程中，由于受到机床精度、伺服系统动态特性不匹配等因素的影响，难免会产生轮廓误差。近年来，如何补偿并减小轮廓误差已经成为一个研究热点。

轮廓误差控制一般有两种方法：一是通过控制各轴跟随误差来间接达到减小轮廓误差的目的。如孙兴伟[1]提出的前馈加反馈的复合控制方法能有效地减小跟随误差，从而减小零件轮廓误差。二是直接控制轮廓误差。如Koren[2]提出的交叉耦合控制器，可以将轮廓误差补偿量分配到各联动轴，实现各轴之间的协同控制。后来，人们对其进行了多方面的改进，设计了不同类型的交叉耦合控制器[3-6]，但大部分都是针对两轴或三轴机床的。对于五轴机床，由于增加了旋转轴，刀具运动变得更加复杂，轮廓误差不仅与刀心位置有关，还与刀轴姿态有关。所以对于五轴数控机床，存在着两种轮廓误差：刀心位置轮廓误差和刀轴方向轮廓误差。孙开珊[7]利用空间解析几何的方法对四轴和五轴机床建立了误差分配模型，但只计算了三个平动轴方向上误差补偿量，而对于转动轴则没有进行额外的补偿。霍彦波[8]对转动轴与平动轴联动加工圆弧时的轮廓误差进行了分析，但没有考虑刀轴方向对轮廓误差的影响。Sencer[9]针对五轴机床提出了一种多输入多输出的连续时间积分滑块模型控制器，能同时减小刀心位置轮廓误差和刀轴方向轮廓误差。

本文首先建立了双转台五轴机床的运动学模型，分析了各进给轴对刀心位置轮廓误差和刀轴方向轮廓误差的影响规律；在此基础上设计了一种五轴联动数控机床轮廓误差补偿控制方法，该方法能同时减小刀心位置轮廓误差和刀轴方向轮廓误差；最后用Matlab程序对其有效性进行了验证。

1双转台五轴机床运动学建模

CAM系统根据零件表面特征，生成工件坐标系下的刀位数据，包括参考刀心位置坐标和参考刀轴方向矢量。要把这些数据转化为伺服系统的控制数据，需要对机床进行运动学建模：求解各轴的关节变量与刀具在工件坐标系中的位置姿态的映射关系。五轴数控机床运动学建模包括运动学正解和运动学逆解模型。

图1　双转台五轴联动数控机床示意图

1.1运动学正解模型

已知五个进给轴的运动位置分别为x，y，z，α，γ，求工件坐标系下的刀心位置坐标和刀轴方向矢量。用s和c分别表示sin和cos，则坐标转换矩阵为:

T=Trans(Qx,Qy,Qz)·Rot(C,-γ)·

Rot(A,-α)·Trans(-x,-y,z)=

(1)

则刀心位置坐标为:

(2)

刀轴方向矢量为:

(3)

当五个轴的偏差分别为dx、dy、dz、dα、dγ时，刀心位置偏差为:

(4)

由式(4)可知，刀心位置偏差的X方向、Y方向分量与五个轴的偏差都有关，而Z方向分量只与Y轴、Z轴、A轴的偏差有关。

刀轴方向偏差为:

(5)

由式(5)可知，刀轴方向偏差的X方向、Y方向分量与两个旋转轴的偏差有关，而Z方向分量只与A轴偏差有关。

1.2运动学逆解模型

(6)

由式(2)可得：

(7)

2轮廓误差计算模型

2.1刀心位置轮廓误差计算模型

五轴机床的刀心位置轮廓误差被定义为实际刀心位置到理论轮廓曲线的最短距离。如图2所示，设Pn为当前采样周期理想插补点，Pn-i为Pn前面第i个插补点，Pa为当前采样周期实际刀心位置，e为跟随误差；εt为理论上的刀心位置轮廓误差。

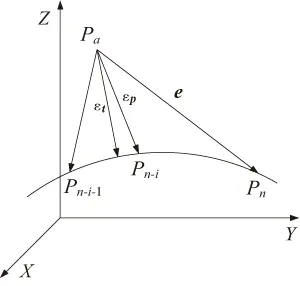
图2　刀心位置轮廓误差模型

提出的刀心位置轮廓误差计算方法为：依次计算并比较当前实际刀心位置Pa与插补点Pn、Pn-1、Pn-2、Pn-3、Pn-4之间的距离，若在点Pn-i处得到最小值，则把PaPn-i=εp近似作为刀心位置轮廓误差。点Pn-i称为轮廓误差计算点或轮廓误差补偿点。

2.2刀轴方向轮廓误差计算模型

五轴机床的刀位数据文件中，每个刀心位置都对应一个刀轴方向。由于刀轴方向矢量都是单位矢量，若把矢量起点放在原点，则矢量终点将在一个半径为1的球面上移动，其轨迹称为刀轴方向轨迹。

本文把五轴机床的刀轴方向轮廓误差定义为轮廓误差补偿点处的刀轴方向矢量与实际刀轴方向矢量之间的夹角。如图3所示，设Or为当前采样周期轮廓误差补偿点Pn-i处的参考刀轴方向矢量；Oa为实际刀轴方向矢量，则本文定义的刀轴方向轮廓误差为:

εo=

(8)

当εo用弧度表示时，其大小等于Or和Oa两个矢量终点之间球面圆弧的长度，近似等于对应的弦长，即：

(9)

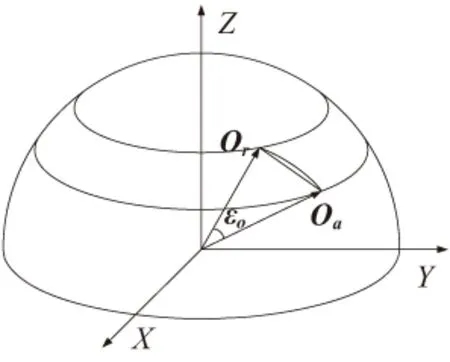
图3　刀轴方向轮廓误差模型

3轮廓误差补偿控制方法

为了达到理想的加工精度，需要同时对刀心位置轮廓误差和刀轴方向轮廓误差补偿控制，本文提出的控制方法如图4所示。

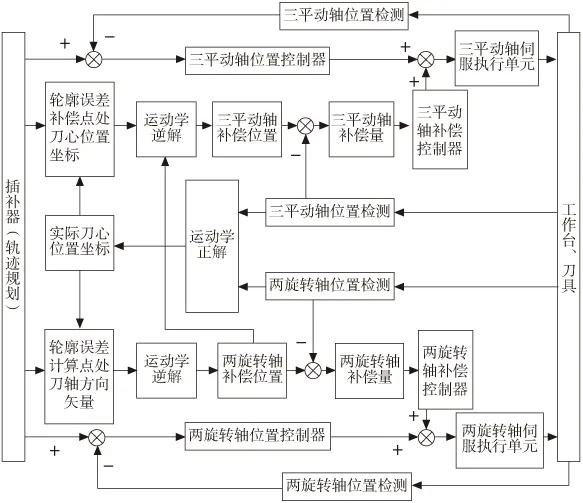
图4　轮廓误差控制方法

在第k个采样周期，通过三平动轴和两旋转轴的光栅尺检测各轴的实际位置xa、ya、za、αa、γa，与插补器输出的理想位置对比，计算出各轴的跟随误差，然后分别输入到各轴的位置控制器(采用PID控制器)中，得到各轴的控制电压量Ux(k)、Uy(k)、Uz(k)、Uα(k)、Uγ(k)。

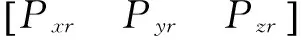
用各轴补偿位置xr、yr、zr、αr、γr减去检测到的实际位置xa、ya、za、αa、γa，即可得到各轴的补偿量Δx(k)、Δy(k)、Δz(k)、Δα(k)、Δγ(k)，输入到轮廓误差补偿控制器(采用PI控制器)之后得到各轴的电压补偿量，例如X轴电压补偿量为：

(10)

式中KPx、KIx分别为PI控制器的比例、积分系数。最后把各轴电压补偿量叠加到各轴控制电压量后输入到各轴的伺服执行装置。

4轮廓误差补偿控制效果验证

一个典型的进给伺服系统方框图如图5所示。图中u为输入电压信号，Ka为电流放大器增益，Kt为电机转矩常数，J为等效转动惯量，B为等效粘性阻尼，Rg为传动增益，v为输出的位移信号或角度信号。这里暂且不考虑由其他因素引起的干扰，则进给伺服系统的开环传递函数为：

(11)

图5　进给系统方框图

采用如表1所示的机床参数进行仿真。

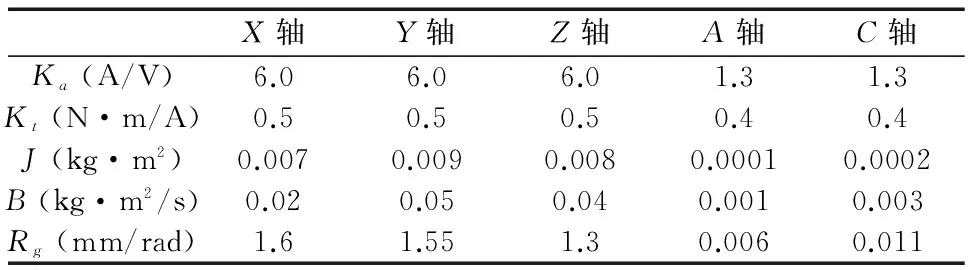
表1　机床加工参数

设参考刀心位置轨迹为螺旋线，参数方程为：

(12)

设刀轴方向轨迹为半径为1的球面与一个圆柱体的交线，其参数方程为：

(13)

使用轮廓误差补偿控制器之前，轮廓误差曲线如图6所示；使用轮廓误差补偿控制器之后，轮廓误差曲线如图7所示。

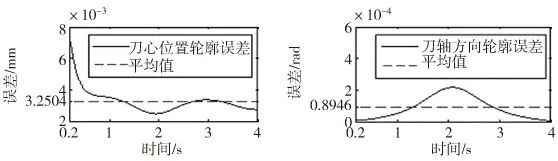
图6　使用轮廓误差补偿控制器之前轮廓误差曲线

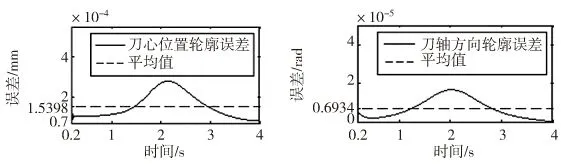
图7　使用轮廓误差补偿控制器之后轮廓误差曲线

由Matlab仿真结果可知，使用轮廓误差补偿控制器之后，刀心位置轮廓误差平均值由使用前的3.2504×10-3mm降低到1.5398×10-4mm；刀轴方向轮廓误差平均值由使用前的0.8946×10-4rad降低到0.6934×10-5rad。这两种轮廓误差均大幅度减小，说明提出的轮廓误差补偿控制方法效果明显。

5结束语

本文建立了双转台五轴数控机床的运动学模型，包括运动学正解和运动学逆解，并得出结论：刀心位置轮廓误差与五个轴的误差都有关，而刀轴方向轮廓误差只与两个旋转轴的误差有关。提出了一种基于运动学正逆解模型的轮廓误差补偿控制方法，并进行了仿真验证。对于五轴联动数控机床，在每个采样周期综合考虑刀心位置轮廓误差和刀轴方向轮廓误差，对五个进给轴进行补偿控制，可有效提高机床轮廓精度。

[参考文献]

[1] 孙兴伟,董蔚,王可,等.数控机床伺服系统跟随误差对加工轮廓的影响[J].制造技术与机床,2010(6):76-78.

[2]YKoren.Cross-CoupledBiaxialComputerControlforManufacturingSystems[J].ASME, 1980,102(4): 265-272.

[3] 丛爽,刘宜.多轴协调运动中的交叉耦合控制[J].机械设计与制造,2006(10):166-168.

[4] 王丽梅,武志涛,孙宜标,等.直接驱动XY平台轮廓误差分析及法向交叉耦合控制[J].电机与控制学报,2010,14(9):63-68.

[5] 周延松.三轴数控系统的轮廓误差补偿方法研究与实现[D].杭州:浙江工业大学,2013.

[6] 赵欢,朱利民,丁汉,等.基于高精度轮廓误差估计的交叉耦合控制[J].机械工程学报,2014,50(3):158-164.

[7] 孙开珊.多轴空间轮廓误差的建模与交叉耦合补偿[D].武汉:华中科技大学,2007.

[8] 霍彦波,丁杰雄,谢东,等.五轴数控机床转动轴与平动轴联动的轮廓误差仿真分析[J].组合机床与自动化加工技术,2012(3):21-24.

[9]BSencer,YAltintas.ModelingandControlofContouringErrorsforFive-AxisMachineTools—PartII:PrecisionContourControllerDesign[J].ASME,2009,131(3):1-10.

[10] 陈则仕,张秋菊.D-H法在五轴机床运动学建模中的应用[J].机床与液压,2007,35(10):88-90.

(编辑赵蓉)

Contour Error Control Approach of Five-axis Linked CNC Machine Tools with Double Rotating Table

ZHUANG Bing-yuan, ZHAO Guo-yong, ZHAI Jing-tao, HOU Chun-hong

(Department of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255049, China)

Abstract：In five-axis CNC machining, the various errors caused by geometric precision, dynamic characteristics mismatching of the machine tools will result in the part contour errors. So it is important to control and compensate the contour errors. The kinematic model of five-axis machine tools with double rotating table was established based on D-H method. Through forward kinematics, the axial motion laws causing the tool tip contour error and the tool orientation contour error were obtained, which could provide a theoretical foundation for the contour error compensation control. At last, a contour errors control approach based on the kinematic model was developed. It has been proved to be effective through simulated experiment.

Key words：kinematic model; tool tip contour error; tool orientation contour error; error compensation

文章编号：1001-2265(2016)06-0103-03

DOI:10.13462/j.cnki.mmtamt.2016.06.027

收稿日期：2015-07-29;修回日期：2015-08-18

*基金项目：国家自然科学基金项目“五轴联动数控轮廓误差耦合控制理论与方法研究”(51105236)

作者简介：庄丙远(1989—)，男，河南舞阳人，山东理工大学硕士研究生，研究方向为数控技术与装备；通讯作者：赵国勇(1976—)，男，山东淄博人，山东理工大学教授，博士，研究方向为机械制造自动化技术，(E-mail)zgy709@126.com。

中图分类号：TH165;TG659

文献标识码：A