磁悬浮永磁直线电动机自抗扰控制器设计*

蓝益鹏，刘宇菲

(沈阳工业大学 电气工程学院，沈阳 110870)

磁悬浮永磁直线电动机自抗扰控制器设计*

蓝益鹏，刘宇菲

(沈阳工业大学 电气工程学院，沈阳 110870)

摘要：磁悬浮永磁直线电动机实现了直接驱动和无摩擦进给，有效提高伺服系统的反应速度和精度。针对电动机运行中受到系统外扰和内扰的问题，将自抗扰控制器引入磁悬浮永磁直线电动机。首先，建立电动机在d-q坐标下的数学模型，分析系统非线性强耦合的本质原因；其次，将速度，d，q轴电流作为系统状态量，设计三个一阶自抗扰控制器。将电流间存在的耦合项视为系统内部扰动，应用扩张状态观测器估计系统输出和受到的综合扰动，并在反馈中加以补偿，实现系统的反馈线性化；最后，建立采用自抗扰控制的系统仿真模型。仿真结果表明，采用自抗扰控制的磁悬浮永磁直线电动机伺服系统具有良好的动态性能，并且能有效抑制内外扰动，具有很强的鲁棒性。

关键词：磁悬浮永磁直线电动机；自抗扰控制；解耦控制；反馈线性化

0引言

磁悬浮永磁直线同步电机兼有永磁电机和直线电机各自独特的优势，并且具有运行可靠，结构简单，非接触，无摩擦的特点，因而在精密加工、电子装配线和仪器仪表业有着广泛的应用，是高速精密数控加工的理想驱动元件[1-2]，但是由于伺服系统取消了全部中间环节，负载和外部干扰直接作用于伺服系统，严重损害系统运行的平稳性和精度[3]，所以在高速高精度场合，必须降低这些扰动对系统的影响。

自抗扰控制器(Auto Disturbances Rejection Controller，记作ADRC)技术的提出源于PID控制的思想，韩京清教授针对经典PID控制进行了改进，提出了自抗扰控制技术。自抗扰控制器包括：跟踪微分器(TD)，扩张状态观测器(ESO)和非线性状态误差反馈(NLSEF)三部分，是一种基于过程误差的调节方法，能自动补偿被控对象的失配和来自外界的扰动，具有很强的抗干扰能力[4-6]，其最大优点是不依赖被控对象的具体数学模型，广泛应用于复杂，不确定性非线性系统中[7]。

本文将对磁悬浮永磁直线电动机设计ADRC控制器，对电动机的速度，电流id和iq分别控制，将电流子系统中的耦合项视为扰动，实现电动机的动态解耦控制，很好的抑制了模型中非线性因素和外部干扰。

1数学模型

对磁悬浮永磁直线电动机矢量控制时，假设铁心饱和可以忽略，且反电动势是正弦的，气隙磁阻可转成傅立叶级数，磁势沿气隙以正弦分布，并且不计涡流和磁滞损耗。磁悬浮永磁直线伺服系统在d-q轴下的数学方程为：

(1)

(2)

其中，ud,uq,id,iq,Ld,Lq,ψd,ψq分别为d-q坐标系下的动子电压，电流，电感和磁链，ψf为永磁体励磁磁链，Rs为动子电阻，v为动子线速度，np为极对数，τ为极距。

动子电磁推力方程为：

(3)

当Ld=Lq=L，电磁推力为：

Fe=Kfiq

(4)

Kf为电磁推力系数：

(5)

由于电动机动子处于悬浮状态，与导轨之间无摩擦，则机械运动方程为[8]：

(6)

其中，M为动子质量，Fl为负载阻力，Fd为端部效应力。

由式(1)、(2)、(4)、(6)得到磁悬浮永磁直线电动机在d-q坐标系下的状态空间模型为：

(7)

从状态方程中可以看出，磁悬浮永磁直线电动机是一个多变量，强耦合，非线性的系统，其中电流id的状态方程中含有iq和v的耦合项，iq的状态方程中含有id和v的耦合项，这些来自系统内部的耦合项的存在使电流方程成为非线性方程，对系统性能造成极大干扰；速度方程中存在负载变化和端部效应力变化的不确定因素，影响电动机的平稳运行，所以设计控制器时需要对干扰项进行抑制。

2自抗扰控制

2.1非线性跟踪微分器(TD)

非线性跟踪微分器将非线性方法引入微分器设计中，根据参考输入和受控对象的限制安排过渡过程并提供这个过程的各阶导数，能够有效减小系统初始误差，并解决系统响应快速性和超调之间的矛盾[9]。本文对各个状态量采用一阶TD设计，数学描述为：

(8)

(9)

其中，α为非线性因子，δ为滤波因子，都为可调系数，当α<1时，fal函数具有大误差小增益，小误差大增益的特性[10]。

2.2扩张状态观测器(ESO)

扩张状态观测器采用非光滑结构，能观测出被控对象的各个状态量和作用在被控对象上的综合扰动，包括系统内扰和外扰。扩张状态观测器与系统无关，只与扰动变化率有关，由于实际情况中总扰动有界，因此状态观测器可以实现对未知扰动的实时观测。一阶扩张状态观测器数学描述如下：

(10)

其中，w为系统输出，u为控制输入，b为系统参数，β21,β22为可调参数，变量z22称为被扩张的状态。

2.3非线性状态误差反馈(NLSEF)

NLSEF利用TD的输出和ESO的输出之间的误差计算状态误差反馈控制量，再对ESO观测到的外部扰动进行补偿，从而实现对被控对象的反馈线性化，最终生成控制量。一阶NLSEF的数学描述为：

(11)

3控制器设计

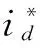
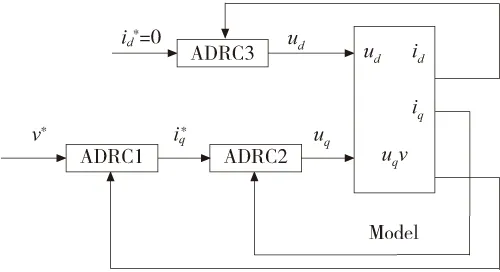
图1　采用ADRC的系统结构图

图中，ADRC1为速度自抗扰控制器，ADRC2和ADRC3分别为电流iq和id的自抗扰控制器，每个控制器都为一阶，利用这3个一阶控制器可以实现系统扰动自动补偿，保证系统对参考信号的稳定跟踪并抑制内外扰动。

仿真过程中的重点是控制器参数的调整。ADRC涉及的可调参数较多，通常采取分离性原则，按照先内环后外环的顺序，各部分参数调整的简略方法如下：

(1)δ1,δ22,δ3是fal函数线性区间的长度，与误差范围有关，一般取很小的值，但过于小容易产生高频振荡，根据经验取0.1左右，仿真中根据实际需要设定。

(2)α1,α22,α3为fal函数的指数因子，一般取[0，1]。

(3)β1,β21,β22,β3是对系统性能影响最大的参数。β1和β3在一定范围内越大，系统的跟踪效果越好；β21与β22决定了ESO的性能，β21较小导致z21跟踪较慢，过大会引起振荡，β22一般比β21大1～2个数量级。这些参数范围较大，一般不容易确定，可参照文献[11-13]的参数调整方法进行。

4仿真研究

在matlab环境下建立采用ADRC的磁悬浮永磁直线电动机控制系统simulink模型。电动机相关参数如下：M=50kg,Rs=1.6878Ω,L=25.92mH,

np=3,ψf=0.1754Wb,τ=33mm。给定阶跃信号作为速度参考信号，仿真结果如下：

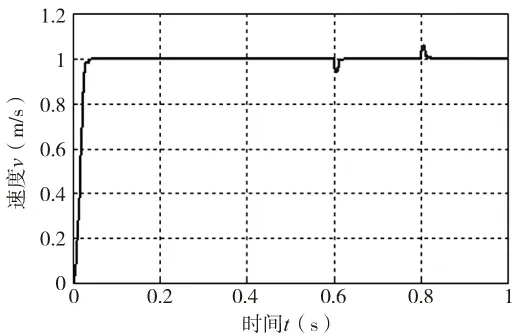
图2　速度响应曲线

图3　电流iq响应曲线

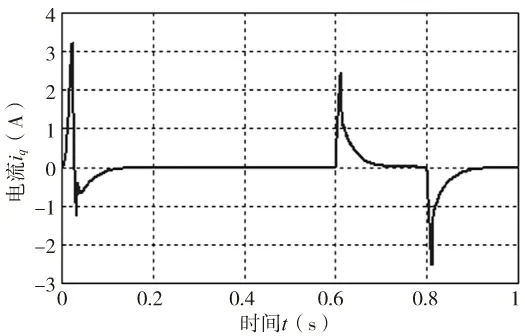
图4　电流id响应曲线

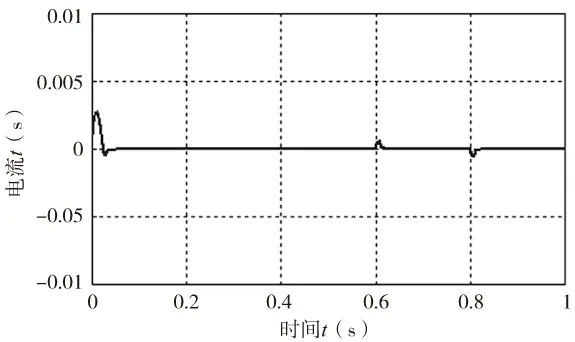
图5　ESO对速度参考信号的跟踪误差

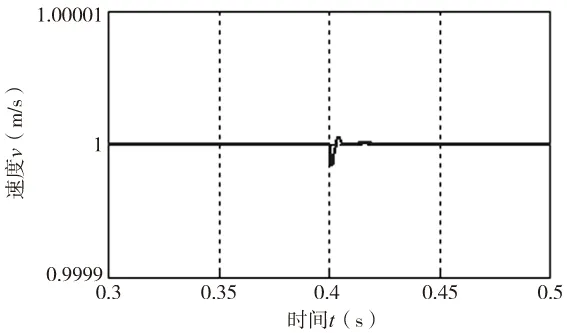
图6　电阻变化时速度响应曲线(局部放大)

在0.6s时外加25N负载扰动，0.8s时卸掉负载，图2～图4分别为速度v，电流iq和id的响应曲线，如图所示，速度能在0.1s内迅速跟踪参考信号，达到稳定并且无超调；电流iq和id开始存在震荡，但可以在0.1s内迅速平稳，系统响应在外加负载后能迅速恢复到稳定状态，说明采用ADRC的控制策略使系统获得良好的动态性能；图5为ESO对速度的估计与参考信号之间的误差，最大误差不到0.005，说明ESO能有效观测系统状态量；图6为0.4s时，电阻变化后速度响应曲线的局部放大图，由图可见，电阻变化对系统状态的影响非常小。所以，无论是外部扰动还是由系统本身参数变化导致的内部扰动，ADRC控制器具有较强的抗干扰能力，能使系统具有较好的动态性能和很强的鲁棒性。

5结论

对于具有内扰和外扰同时作用的磁悬浮永磁直线电动机伺服系统，采用三个一阶ADRC控制器对系统的速度v，电流iq和id分别进行控制，利用扩张状态观测器对扰动的观测作用，对电流间存在的耦合进行解耦，再对扰动进行补偿，实现系统的反馈线性化。仿真结果表明，ADRC控制下的系统具有良好的动态性能，对于内扰和外扰能有效抑制，具有很强的鲁棒性。

[参考文献]

[1] 仇翔，俞立，南余荣．永磁同步直线电机控制策略综述[J].微特电机，2005(10)：39-43．

[2] 江思敏，王先逵，钱磊．全数字反馈高性能永磁直线电动机的机电系统设计[J]．中国机械工程，2002，13(11)：967-969．

[3] 张代林，陈幼平，艾武,等．基于光测模型的直线电机干扰抑制技术的研究[J]．中国电机工程学报，2007，27(12)：14-18．

[4] 韩京清．自抗扰控制技术[M]．北京：国防工业出版社，2008．

[5] 黄本润，夏立，吴正国．自抗扰控制器在动态电压恢复器中的应用[J]．电机与控制学报，2012，16(6)：106-110．

[6] Wu Dan，Chen Ken．Design and analysis of precision active disturbance rejection control for noncircular turning process[J]．IEEE Transactions on Industrial Electronics，2009，56(7)：2746-2753．

[7] 王松．永磁同步电机的参数辨识及控制策略研究[D].北京:北京交通大学,2011.

[8] 田录林，张靠社，王德意,等．永磁导轨悬浮和导向磁力研究[J]．中国电机工程学报，2008，28(21)：135-139．

[9] 刘清．基于自抗扰控制器的永磁同步电机伺服系统控制策略的研究及实现[D]．天津:天津大学，2011．

[10] 黄庆，黄守道，陈泽远,等．不对称电压下PWM整流器的变结构自抗扰控制[J]．电机与控制学报，2014，18(1)：50-55．

[11] 韩京清，张荣．二阶扩张状态观测器的误差分析[J]．系统科学与数学，1999，19(4)：455-471．

[12] 张荣，韩京清．串联型扩张状态观测器构成的自抗扰控制器[J]．控制与决策，2000，15(1)：122-124．

[13] 康忠健，陈学允．非线性扩张状态观测器的一种设计方法[J]．电机与控制学报，2001，5(3)：199-203．

(编辑赵蓉)

Auto Disturbances Rejection Controller Design of Magnetic Levitation Permanent Magnet Linear Motor

LAN Yi-peng，LIU Yu-fei

(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)

Abstract：Maglev permanent magnet linear motor achieves direct drive and frictionless feed and improves the response speed and precision of the servo system effectively. In view of the problem that motor disturbs by the external disturbances and perturbation in operation, introduce the ADRC to the maglev permanent magnet linear motor. First, establish the mathematical model in d-q coordinates and analysis the essential reasons of nonlinear and strong coupling. Second, design three ADRC controllers of one order with regarding the speed, d, q axis current as the system state quantities. The coupling between the currents will be seen as disturbances of the inner system, using the extended state observer to estimate the system output and the comprehensive disturbances, compensate in the feedback to realize the feedback linearization of the system. Finally, establish the simulation model of the control system. The result shows that, the maglev permanent magnet linear motor servo system with ADRC has well dynamic performance, restrains the internal and external disturbance effectively and has strong robustness.

Key words：magnetic levitation permanent magnet linear motor; ADRC; decoupling control; feedback linearization

文章编号：1001-2265(2016)06-0096-03

DOI:10.13462/j.cnki.mmtamt.2016.06.025

收稿日期：2015-07-16

*基金项目：国家自然科学基金资助项目(50975181)

作者简介：蓝益鹏(1962—)，男，陕西华县人，沈阳工业大学副教授，硕士生导师，研究方向为数控技术、鲁棒控制，(E-mail)lanyipengg@163.com。

中图分类号：TH166;TG659

文献标识码：A