数控机床服役态全行程尺寸关系模型研究*
马军旭,金 涛,胡 敏,赵万华
(西安交通大学 机械制造系统工程国家重点实验室,西安 710054)
数控机床服役态全行程尺寸关系模型研究*
马军旭,金涛,胡敏,赵万华
(西安交通大学 机械制造系统工程国家重点实验室,西安710054)
摘要:重力、热等造成机床在装配时的精度发生变化,因此在机床精度设计时应考虑服役态因素的影响。文章提出一种考虑服役态影响的尺寸关系模型用于机床精度设计。首先对基础件进行离散表征,利用尺寸链理论,建立了服役态全行程尺寸关系模型。其次给出了服役态下尺寸关系模型中各环的等效尺寸计算方法。最后以某型号机床Y轴尺寸为例,进行了服役态全行程尺寸关系模型实验验证。结果显示:在全行程范围内,封闭环尺寸实测值与利用服役态尺寸关系模型得到的计算值最大相差2.2μm,封闭环尺寸实测值与几何态封闭环尺寸计算值最大相差3.8μm,服役态尺寸关系模型更接近于实际情况。
关键词:服役态;全行程;离散表征;尺寸关系模型
0引言
数控机床几何精度占数控机床精度的70%以上。通常通过设计制造(主动)和补偿(被动)两种措施保证机床几何精度。在几何精度设计时,使用尺寸链进行公差分析与设计。
从1978年Hillyard R.C.博士[1]首次提出计算机辅助确定零件的几何形状、尺寸和公差的概念开始,公差模型经历了属性模型[2]、漂移模型[3]、参数化模型[4]、运动学模型[5]、自由度模型[6]等时期。利用公差模型进行公差分析,提出了基于齐次转换矩阵方法[7]、矢量环及直接线性化方法[8]、基于雅克比矩阵的虚拟接点法[9]、约束自由度模型[10]、矢量公差法[11]、Gap-Space方法[12]和扩展空间技术[13]等方法或技术。利用公差模型进行公差设计,建立了一系列的公差-成本模型[14-15]、公差优化算法[16-18]、公差综合模型[19-20]等,出现了一系列的公差设计理论,如:矢量公差设计[21]、并行公差设计[22]、鲁棒公差设计[23]和动态公差控制[24]等。
上述文章主要针对公差模型、公差分析和公差设计,利用多体系统理论、小位移旋量理论、齐次坐标变换方法、模拟退火算法、遗传算法和模糊神经网络等建立了不同的数学模型,研究了公差的建模方法,公差大小是否满足几何功能要求、是否满足可装配性、可制造性以及制造成本等CAT问题。

图1 服役态与几何态对比示意图
如图2所示,图2a表示固定件是刚体,移动件在不同位置时,固定件尺寸、移动件尺寸和封闭环尺寸关系,此时A1=A3。图2b表示固定件是柔体,移动件在不同位置时,三者间的尺寸关系,此时A1≠A3。
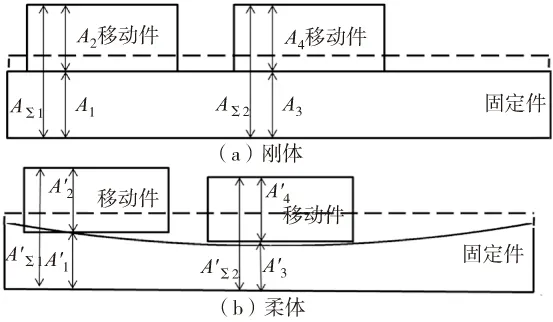
图2 在全行程不同位置对比刚体与柔体变形示意图
因此,数控机床在精度设计时,需要考虑全行程不同位置时服役态的影响,上述模型或方法不能很好地满足这种情况。
本文的目的是建立用于公差设计的服役态尺寸关系模型。利用离散点尺寸描述全行程内固定件的尺寸变化,根据尺寸链理论建立全行程服役态尺寸关系模型。计算在全行程不同位置处,服役态因素造成的封闭环尺寸变化。
2服役态尺寸变化模型
2.1几何要素的离散与表征
由于传统的尺寸链中,直线和平面简化成理想情况所造成的不足,建立服役态尺寸关系模型时,需要对零部件中与尺寸相关的几何要素(线、面)重新进行表征。如图3所示,把固定件沿X方向离散成若干份。离散原则如下:
(1)测量基准视为理想要素,没有误差。
(2)运动方向等距离离散。
在离散后的物体上放置一个坐标系XOY,称为零件坐标系,任一位置的尺寸利用特征点坐标表示。点P的坐标为Pi(xi,yi),测试基准与X轴的距离为y0,则在全行程内不同位置处,固定件尺寸为
Ly(xi)=yi+y0i=1…n
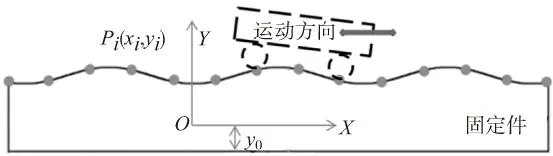
图3 尺寸与坐标关系示意图
2.2服役态尺寸关系模型
如图4所示的数控机床直线运动轴部件,通常由固定件(床身等)、导轨滑块系统(直线导轨或静压导轨灯)和移动部件(工作台等)组成,在进给方向(Y方向)上由螺母丝杠或者直线电机驱动。
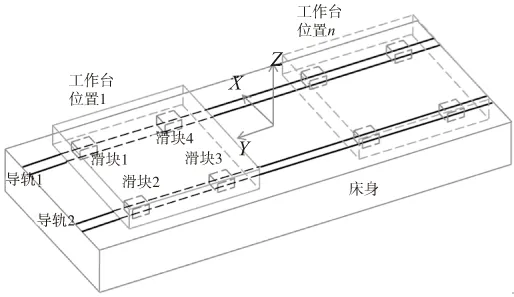
图4 机床直线轴结构示意图
设在Y方向全行程内分成n段,则工作台在全行程有(n+1)个位置。在导轨1和导轨2上,分别有2(n+1)个位置与滑块相对应。取2(n+1)个点的坐标代替床身的Z向尺寸。如图5所示。

图5 床身尺寸离散示意图
根据尺寸链理论,在全行程任一位置,建立工作台与地面(理想基准)的服役态尺寸关系模型,如图6所示。则服役态全行程尺寸关系模型为:
AΣi=A1i+A2ii=1…n
(1)

图6 服役态尺寸关系模型
2.3封闭环尺寸的计算
由服役态尺寸关系模型可知,组成环为固定件尺寸A1i和移动件尺寸A2i;封闭环为AΣi。
在全行程的任一位置,床身尺寸(固定件尺寸)由滑块尺寸决定。
在Y轴不同位置处,固定件尺寸A1i的等效尺寸为:
(2)
A滑块是滑块位置对应的床身尺寸。由加工后尺寸和服役态变形共同决定,在全行程内随滑块位置变化。
本文仅以俯仰造成的尺寸变化为例等效移动件尺寸。在Y轴不同位置处,移动件尺寸A2i的等效尺寸为:
(3)
A2为移动件的理想尺寸;L为滑块在Y向的间距,如图7所示。
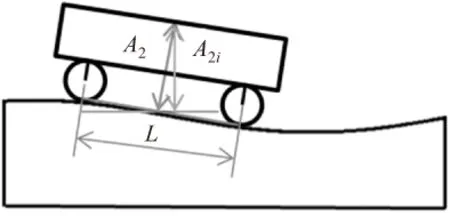
图7 尺寸A2i等效示意图
由公式(1)、(2)、(3)即可得到封闭环尺寸。
3实验方法
本实验的目的是验证在全行程不同位置时,服役态因素(此时只考虑重力)造成的封闭环尺寸变化,以及本文所提出的方法有效性。
图8呈现的是本文的实验装置。包括两个部分:某型号机床和激光跟踪仪。激光跟踪仪Laser Tracker Leica TN90精度为3μm。

图8 实验测试图
本文中,实验分两步进行。第一步,拆下工作台,分别在两个导轨上推动滑块,建立固定坐标系。在Y方向全行程分成5段,在离散的不同位置处,利用激光跟踪仪采集滑块在固定坐标系下的坐标值。根据离散数量,两根导轨共采集24个点。第二步,安装工作台。激光跟踪仪保持不动,保证测试在同一个坐标系进行。在离散的6个位置处,以工作台上一点代替工作台表面,分别采集其在固定坐标系的坐标值。不论导轨滑块坐标值测试点还是工作台上测试点,每个测试点重复采集五次坐标值,各点的坐标值由五次平均得到。
利用游标卡尺(精度为0.01mm)分别在四个滑块位置测试工作台尺寸,每个位置测试五次,取平均值作为工作台尺寸(移动件尺寸)。
由尺寸和坐标的关系可知,固定件尺寸A1i和封闭环尺寸AΣi由坐标测试值和坐标轴到尺寸测试面的距离决定。本文采用坐标测试值代替A1i和AΣi,相当于测试基准由固定件底面变为坐标系坐标轴,不影响计算结果的准确性。
测试时,环境温度变化在24.2±0.2℃以内。
4结果和讨论
表1所示为工作台拆下后(几何态),在Y轴行程不同位置处,由公式(2)计算得到的床身尺寸等效坐标值;以及工作台重力造成床身不同位置处变形后(服役态),床身尺寸等效坐标值。由表可知,工作台安装到床身后,在工作台重力作用下,Y轴不同位置处的床身尺寸不同。床身尺寸变化的最小值为2.5μm,最大值为2.9μm。
游标卡尺测试得到工作台平均尺寸为95.81mm。由公式(3)计算得到工作台尺寸等效坐标值,如表2所示。
由公式(1)计算分别得到几何态和服役态下封闭环尺寸如表3所示。
由激光跟踪仪测试得到的装配后工作台尺寸(封闭环尺寸)坐标值如表3所示。
图9为封闭环尺寸实测值、服役态计算值和几何态计算值的对比图。
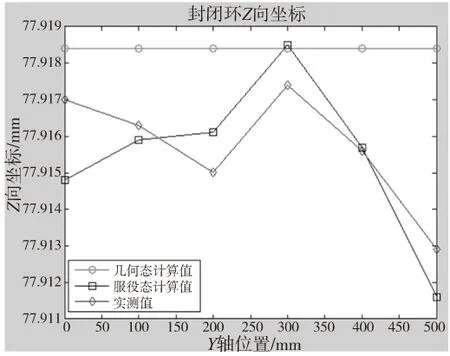
图9 封闭环尺寸实测值、服役态计算值及几何态计算值对比

Y轴位置(mm)0100200300400500床身坐标(mm)几何态-17.8951-17.8938-17.8938-17.8915-17.8941-17.8982服役态-17.8892-17.8900-17.8931-17.8906-17.8925-17.8937床身尺寸变化量(μm)5.93.80.70.91.64.5

表2 Y轴不同位置处工作台尺寸等效后的坐标值

表3 服役态、几何态计算值与实测值对比表
在Y轴全行程不同位置处,封闭环尺寸是变化的。只考虑几何状态时,封闭环尺寸为77.9185mm,考虑服役态时,全行程内,封闭环尺寸最大差值为6.9μm,实测值最大差值为4.5μm。只考虑几何状态时,床身尺寸是由不同位置的测试值平均得到的一个数值。由于床身尺寸采用离散表征,服役态造成在全行程不同位置时,床身尺寸的变化是不同的。由此也会造成移动件的姿态变化,冯更新[25]等的研究证明了磨床中确实存在这种姿态变化。
在服役态和几何态两种情况下,封闭环尺寸计算值是不相同的。几何态计算值和服役态计算值最大相差6.0μm,平均值相差3.1μm。这是由于重力作用造成的尺寸变化。文中只考虑了重力的影响,机床在使用过程中,其他因素(热、装配应力等)也会造成服役态尺寸变化。
测试值与服役态计算值最大相差2.2μm,各点偏差的平均值1.03μm;与几何态计算值最大相差3.8μm,各点偏差的平均值2.78μm。这说明考虑服役态影响的计算结果比几何态的计算结果更符合实际情况。
5结论
通过理论分析和实验测试得到如下结论:
(1)本文建立了服役态全行程尺寸关系模型。利用此模型计算出的服役态全行程尺寸变化量,是进行尺寸设计和精度设计的依据,后续可以依此为基础,研究公差分配和误差补偿问题。
(2)本文利用所建立的模型计算了工作台在重力作用下造成装配后封闭环尺寸的变化量。结果表明考虑服役态影响的尺寸计算比纯几何态的尺寸计算更符合实际情况。
[参考文献]
[1] Hillyard R C. Dimensions and Tolerances in Shape Design [D].London: University of Cambridge, 1978.
[2] Tsai J C, Wang W W. Development of a Computer-Aided Tolerancing System in CAD Environment[M].Global Consistency of Tolerances. Springer Netherlands, 1999: 47-54.
[3] Requicha A A G. Toward a theory of geometric tolerancing[J]. The International Journal of Robotics Research, 1983, 2(4): 45-60.
[4] Krishnan K K, Eyada O K, Ong J B. Modeling of manufacturing processes characteristics for automated tolerance analysis[J]. INTERNATIONAL JOURNAL OF INDUSTRIAL ENGINEERING-APPLICATIONS AND PRACTICE, 1997, 4(3): 187-196.
[5] Desrochers A, Rivière A. A matrix approach to the representation of tolerance zones and clearances[J]. The International Journal of Advanced Manufacturing Technology, 1997, 13(9): 630-636.
[6] Kandikjan T,Shah J J, Davidson J K. A mechanism for validating dimensioning and tolerancing and tolerancing schemes in CAD systems[J]. Computer-Aided Design,2001, 33(10):721-737.
[7] Whitney D E,Gibert O L. Representation of geometric variations using matrix transforms for statistical tolerance analysis in assemblies[J].IEEE International Conference on Robotics and Automation.1993,93(2):314-321.
[8] Chase K W, Magleby S P, Glancy C G. A comprehensive system for computer-aided tolerance analysis of 2-D and 3-D mechanical assemblies[M]//Geometric Design Tolerancing: Theories, Standards and Applications. Springer US, 1998: 294-307.
[9] Laperriere L, Lafond P.Tolerance analysis and synthesis using virtual joints[J].In Proceedings of 6th CIRP Seminars on Computer Aided Tolerancing.Enschede,Nether lands,1999:452-458.
[10] 胡洁,熊光楞,吴昭同.基于变动几何约束网格的公差设计研究.机械工程学报.2003,39(5):20-26.
[11] Weber C,Britten W,Thome O. Conversion of geometrical tolerances into vectorial tolerance representations-A major step towards computer aided tolerancing[C].In International Design Conference, Dubrovnik, 1998.
[12] Zou Z, Morse E P. A gap-based approach to capture fitting conditions for mechanical assembl[J]y.Computer-Aided Design,2004, 36(8):691-700.
[13] Lee S,Yi C. Tolerance analysis for multi-chain assemblies with sequence and functionality constraints[J].In Proceedings of IEEE1997,International Conference on robotics and automation.Albuqyerque,New Mexico,1997.
[14] Bjorke O.Computer-Aided Tolerancing[M].2nded. NewYork:ASME Press,1989.
[15] Dong Z, Hu W, Xue D. New production cost-tolerance models for tolerance synthesis[J].Journal of Engineering for Industry. 1994, 116(3):199-206.
[16] Parkinson D B. Assessment and optimization of dimensional tolerances. Computer-Aided Design. 1985,17(4):191-199.
[17] Lee W J, Johnson G E. Optimal tolerance allotment using a genetic algorithm and truncated Monte-Carlo Simulation[J]. Computer-Aided Design. 1993,25:601-611.
[18] Chase K W,Greenwood W H,Loosti B G,et al. Least cost tolerance allocation for mechanical assemblies with automated process selection[J].Manufacturing Review. 1990.3:49-59.
[19] Pramanik N. A generic framework for design evolution:From function to form mapping to synthesis of tolerances[D]. Syracuse: Syracuse University,2003.
[20] Dantan J Y,Mathieu L,Ballu A,et al.Tolerance synthesis:quantifier notion and virtual boundary[J]. Computer-Aided Design.2005,37(2):231-240.
[21] Humienny Z,Thome O,Weber C.Vectorial dimensioning and tolerancing in computer aided tolerancing[C]. Poland:Proceedings of International Conference Mechatronics,2000, 47-450.
[22] Peng Heping,Jiang Xiangqian,Liu Xiaojun.Concurrent optimal allocation of design and process tolerance for mechanical assemblies with interelated dimension chains[J].International Journal of Journal of Production Research,2008,46(24):6963-6979.
[23] Jeang A.Robust tolerance design by response surface methodology[J].International Journal of Advanced Manufacturing Technology,1999,15:399-403.
[24] McGarvey R G,Lehtihet E A,Castillo E D,et al.On the frequency and location of set point adjustments in sequential tolerance control[J].Internatioanal Journal of Production Research,2001,39(12):2659-2674.
[25] 冯更新.浅析机床动态下的装配尺寸链问题[J].磨床与磨削,1994(2):48-50.
(编辑赵蓉)
Research on Dimension Relationship Model Under Service Conditions in Whole Stroke of CNC Machine Tool
MA Jun-xu, JIN Tao, HU Min, ZHAO Wan-hua
(State Key Laboratory for Manufacturing System Engineering,Xi’an Jiaotong University,Xi’an 710054,China)
Abstract:The precision of CNC machine tools changes in the assembly process due to gravity and thermal effect. So, the effect of the service state on the precision should be considered during the design of CNC machine tools. This paper presents a dimension relationship model under service conditions, which is used for the precision design of CNC machine tools. Firstly, the geometrical feature of fixed part is discretized as a set of coordinate points. Then a dimension relationship model under service conditions in the whole stroke of operation is constructed based on the dimension chain theory. Secondly, the calculation method of the dimensions in the model is developed. Finally, Y-axis dimension of a CNC machine tool is tested to verify the dimension relationship model under service conditions. The results show that at any position in the whole stroke of operation, the biggest different is 2.2μm between the tested values and the calculated values; and the biggest different is 3.8μm between the tested values and the calculated values.
Key words:service conditions; whole stroke; discrete; dimension relationship model
文章编号:1001-2265(2016)06-0092-04
DOI:10.13462/j.cnki.mmtamt.2016.06.024
收稿日期:2015-06-16
*基金项目:国家自然科学基金资助项目(51235009);国家“高档数控机床与基础制造装备”科技重大专项(2011ZX04016-101,2012ZX04005011)
作者简介:马军旭(1981—),男,河南周口人,西安交通大学博士研究生,研究方向为数控机床精度保持性,(E-mail)mx810606@sohu.com;通讯作者:赵万华(1965—),男,辽宁本溪人,西安交通大学教授,博士研究生导师,研究方向为高速、超高速以及精密数控机床集成理论和机电耦合,(E-mail)whzhao@mail.xjtu.edu.cn。
中图分类号:TH162;TG506
文献标识码:A

