基于领域划分的逆向参数化建模*
丛海宸,成思源,杨雪荣,张湘伟
(广东工业大学 机电工程学院,广州 510006)
基于领域划分的逆向参数化建模*
丛海宸,成思源,杨雪荣,张湘伟
(广东工业大学 机电工程学院,广州510006)
摘要:近年来,逆向工程中的参数化建模方法成为研究的重要方向。通过对目前应用比较广泛的基于曲面的逆向参数化建模和基于实体特征的逆向参数化建模的方法分别进行了分析,提出了基于领域划分的逆向参数化建模方法,并详细介绍了这种参数化建模方法的优势及其参数化建模的一般流程。以逆向参数化建模软件Geomagic Design X为平台,通过典型实例参数化建模及误差分析验证了该建模方法的优势,为逆向工程的参数化建模提供了一种更加有效、准确的建模方法。
关键词:逆向工程;领域划分;Geomagic Design X;参数化建模
0引言
随着逆向工程(Reverse Engineering,RE)的发展,其在产品设计开发领域中应用日趋广泛。因参数化建模可实现模型的参数化修改,所以实现逆向参数化建模,能方便对原产品进行二次设计,成为逆向工程发展的新方向[1]。逆向参数化建模已成为消化吸收先进技术,实现新产品快速开发的重要技术手段。
逆向参数化建模方法是在理解原始设计意图的基础上,提取原始设计信息,构建准确的参数化CAD模型[2]。在逆向参数化建模中,我们参考的对象来源于扫描获得的网格模型,通过提取网格曲面的特征,进行逆向参数化建模。本文提出一种基于领域划分的逆向参数化建模方法,通过对原产品网格模型进行领域划分,可实现对不同特征更加准确的分割以及对同一特征不同曲率区域进行辨别,有利于创建非规则特征的参数化模型,对复杂自由形状实现精确拟合,从而创建出准确的参数化CAD模型。该方法可对含有规则特征和非规则特征的复杂形状产品创建出准确的参数化模型,在机械等领域有着广泛的应用前景。
1逆向参数化建模
1.1网格面结构
多边形网格面是实物原型重构的基础[3]。逆向参数化建模过程中,扫描原产品获得点云数据后,需将点云数据进行处理得到多边形网格面,再对多边形网格面进行特征提取创建参数化模型。

图1 多边形网格组成
多边形网格面是由三角形面片拼接组成的,基本元素包括单元面、单元边线、单元顶点及边界[4],如图1所示。单元边线及单元顶点构成三角形单元面,三角形单元面相互拼接,将边界范围内的区域填充形成多边形网格面。
1.2逆向参数化建模方法
目前在逆向工程中的参数化建模方法主要有两类:基于曲面的逆向参数化建模方法和基于实体特征的逆向参数化建模方法。
基于曲面的逆向参数化建模方法是将网格模型根据不同网格面区域(包含单元面、单元边线和单元顶点)所隐含的几何特征进行轮廓线探测,通过轮廓线进行网格区域划分,而后将网格区域拟合,构建几何曲面特征,再进行裁剪、缝合构建出曲面模型,最后将曲面模型导入到正向软件(UG、SolidWorks等)中,进行正向参数化建模,从而得到参数化模型[5]。具体流程图如图2所示。

图2 基于曲面的逆向参数化建模流程
该方法在划定轮廓线时,对轮廓线位置要求较高,如轮廓线位置不准确,会导致拟合曲面所得面片形状发生偏置,且区域拟合时会受偏差较大的单元顶点和单元曲线的影响,产生较大误差,尤其是对非规则自由曲面,在拟合过程中会发生形变。在参数化建模工程中,需要正向、逆向软件操作,建模过程繁琐,建模周期长。
基于实体特征的逆向参数化建模方法是通过对网格面模型进行三维规则特征提取创建基准坐标系,再用基准面或基准面所建平面截取网格模型获得多段线或拟合曲面,然后通过实体参数化建模操作构造出对应的参数化特征,最后通过布尔运算创建出参数化模型[6]。具体流程图如图3所示。

图3 基于实体特征的逆向参数化建模流程
该方法在轮廓线划分区域后,仅能通过规则特征(如平面、圆柱体、圆锥体)创建基准坐标系,对于整体形状非规则产品,无法提取特征基准,创建便于参数化建模的坐标系较为困难。创建非规则特征时,需要进行多次特征编辑(裁剪、求和、求差等),且曲面拟合时也是通过区域进行拟合,会受偏差较大的单元顶点和单元曲线的影响,产生较大误差,不能有效、准确的创建特征复杂的产品参数化模型。因此基于实体特征的逆向参数化建模方法不适合非规则特征、复杂自由曲面的产品的参数化建模。
2基于领域划分的逆向参数化建模
2.1领域的定义
领域是由单元面组成的区域,不含有单元边线和单元顶点,在进行领域划分时,可根据曲率值划分不同特征领域。
在进行特征提取或曲面拟合时,领域会消除单元边线和单元顶点的影响,从而提取出更加规则的特征形状以及拟合出更准确的曲面片。根据曲率划分领域,可以更好地区分不同特征,而且可以对于同一特征的不同曲率形状加以划分,有利于特征的更好表达。
2.2基于领域划分的逆向参数化建模
基于领域划分的逆向参数化建模方法首先是对多边形网格按曲率进行领域划分,将模型特征通过领域组进行表达;然后根据领域创建基准坐标系,进行特征提取创建二维截面线[7]和投影边界轮廓线,并对参数值进行修改和添加线段约束关系,获得更加准确的二维草图,再对草图进行拉伸、旋转、扫描等操作,创建参数化模型;同时根据领域进行曲面拟合,创建面片;最后将面片与参数化模型进行布尔运算,得到准确的原始产品参数化模型[8]。具体流程图如图4所示。

图4 基于领域划分的逆向参数化建模流程
3应用实例
3.1导入数据模型划分领域
通过手持式激光扫描仪获取产品的表面多边形网格数据模型,然后将数据模型以.stl格式文件导入Geomagic Design X中,并进行网格数据模型处理(如:修补模型、简化三角形数量等操作),得如图5所示网格面模型。

图5 产品网格模型
将网格模型按曲率划分领域,并将相同特征领域合并,不同特征领域分割,得到规则特征领域1和领域3,非规则特征领域2和领域4。如图6所示。
按曲率划分领域可以使不同特征更好的进行区分(如领域1和领域2),也可以使同一特征的不同形状区域进行辨别(如扇叶包括正面领域2及背面领域4)。有利于提取规则特征和非规则特征进行多次曲面拟合,更有效地创建参数化模型。
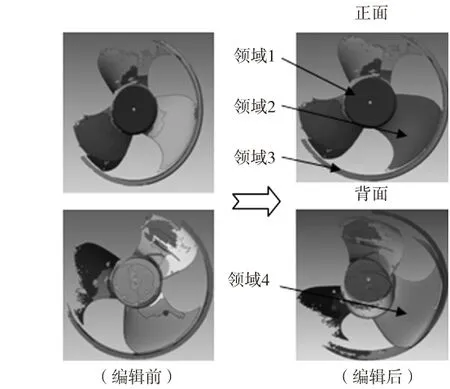
图6 领域编辑
领域组划分完成后,根据领域1和领域3的回转特征创建回转轴线,因回转轴仅根据回转特征领域1和领域3进行提取,排除了其他特征的干扰,因此所提取回转轴位置精度较高。再将领域1进行平面拟合,因领域仅根据单元面进行拟合,消除了单元边线和单元顶点的影响,位置精度会相对较高,且领域1拟合所得平面与领域1特征提取所得回转轴系统会自动默认其垂直关系,拟合出以回转轴为法线的平面,方便建立合理坐标系。然后根据回转轴线与平面创建基准坐标系,获得前基准面、右基准面、上基准面三个基准面[9],如图7所示。
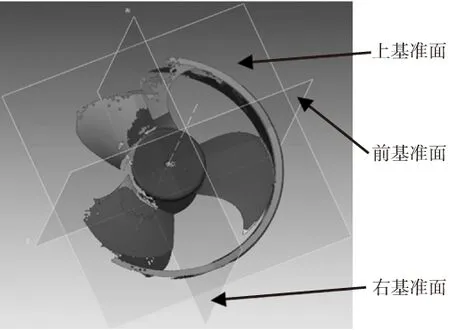
图7 模型基准面创建
前基准面所设置位置数据模型相对较完整,有利于截取规则特征领域1和领域3的截面多段线。领域1所处位置是模型最顶端平面,所以将上基准面设置在此处,有利于投影非规则特征领域2的边界多段线。因此,通过领域不但可以快速的提取出准确、理想的基准轴、基准面,而且根据同一领域提取、拟合同一特征的线或面可方便的判断其几何位置关系,并加以约束,从而有利于创建准确的参数化模型。
3.2特征提取
特征提取是通过软件检测所选择的三维网格面数据中几何体素的曲率特征,并计算几何体素之间的拓扑关系与交点来实现的[10]。根据特征不同,进行特征的截面多段线及投影边界线提取,对各线段几何参数加以修改并对各线段相互位置关系加以约束。
领域1和领域3为规则特征,通过前基准面截取特征,获得截面多段线,并进行参数化修改创建草图,然后将草图轮廓绕回转轴旋转建模,得到参数化模型1,如图8所示。

图8 领域1、3参数化建模操作流程
领域2为非规则特征,通过将模型投影到前基准面,获得边界线曲线,再对曲线进行拟合、约束创建草图,并进行参数化修改,然后将草图轮廓拉伸到领域4建模,得到参数化模型2,如图9所示。

图9 领域2参数化建模操作流程
拉伸到领域功能简化了拉伸实体后再进行曲面拟合并裁剪的过程,从而实现了快速创建参数化模型。
根据领域2进行曲面拟合,创建曲面1。通过领域进行曲面拟合,消除了单元边线和单元顶点的影响,可以拟合出更加光滑、准确的特征曲面。然后以面片为刀具,将参数化模型2进行裁剪[11],获取参数化模型3,如图10所示。

图10 领域拟合后裁剪得参数化模型3
将参数化模型3以回转轴线1进行圆周阵列,便可得到参数化模型4,如图11所示。

图11 参数化模型4
3.3布尔运算
参数化建模后,所得模型仍不是一个完整模型,需通过布尔运算,将各部分模型合并。将参数化模型1、4合并,得到完整参数化实体模型。然后将参数化模型与扫描数据进行偏差分析[11],如图12所示。
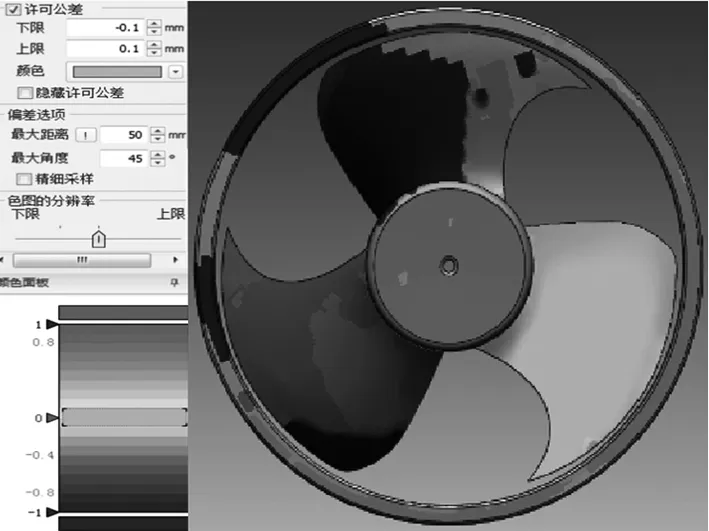
图12 参数化模型与扫描数据偏差分析
观察差值大小,对于差值较大部分,可在参数建模过程中所自动生成的特征树草图里根据提取多段线直接修改参数值,最终得到准确的原产品参数化模型,如图13所示。

图13 参数化模型及其特征树
4总结
本文提出了基于领域划分的逆向参数化建模方法,并分析了这种参数化建模方法的优势及其参数化建模的一般流程。以Geomagic Design X软件为平台,通过创建某风机的转子和叶片的逆向参数化模型为例,证明了该建模方法可以有效地进行特征提取;拟合出较高精度的自由曲面形状;准确、快速的重构产品参数化模型。并以原始采集数据为依据,对参数化模型进行了误差分析,表明该参数化建模方法可为含有规则和非规则特征的复杂产品逆向参数化建模提供一种有效、准确的解决方案。
[参考文献]
[1] 刘军华,成思源,蒋伍,等. 逆向工程中的参数化建模技术及应用[J]. 机械设计与制造,2011(10):82-85.
[2] 成思源,洪树彬,杨雪荣. 逆向工程技术综合实践[M]. 北京:电子工业出版社,2010.
[3] 倪小军. 点云数据精简及三角网格面快速重构技术的研究与实现[D]. 苏州:苏州大学,2010.
[4] 林建立,唐磊, 雍俊海. 多边形网格的非流行封闭三角形网格正则化[J]. 计算机辅助设计与图形学学报,2014,26(10):1557-1566.
[5] 赵忠华. 复杂曲线曲面的参数化建模及多轴运动控制研究[D]. 北京:华北电力大学,2014.
[6] 蔡敏,成思源,杨雪荣,等. 基于Geomagic Design Direct的残缺数据实体重构[J]. 组合机床与自动化加工技术,2015(3):21-23.
[7] 隋亦熙. 逆向工程中曲线曲面特征提取研究[D]. 杭州:浙江大学,2008.
[8] Chang K,Chen C. 3D shape engineering and design parameterization[J]. Computer-Aided Design, 2011,5(8):681-692.
[9] 史庆国. 浅谈基准及其选择[J]. 中国轻工教育,2000(3):41-42.
[10] Bénière R,Subsol G,Gesquière G,et al. A comprehensive process of reverse engineering from 3D meshes to CAD models[J]. Computer-Aided Design,2013,11(45):1382-1393.
[11] 刘炀,陈曦,石鸽娅. 逆向工程技术在曲面重构及检测中的应用[J]. 组合机床与自动化加工技术,2012(1):51-57.
(编辑赵蓉)
Reverse Parametric Modeling Based on Division of Region
CONG Hai-chen,CHENG Si-yuan,YANG Xue-rong,ZHANG Xiang-wei
(Guangdong University of Technology , College of Electromechanics Engineering, Guangzhou 510006,China)
Abstract:In recent years, the method of parametric modeling has become an important direction of research in reverse engineering. This paper analyzed the widely used methods of reverse parametric modeling which are parametric modeling method based on surface and solid feature, and proposes a parametric modeling method based on division of region, and the benefits of this parametric modeling approach and the general process are detailed. With the reverse parametric modeling software Geomagic Design X as platform, the advantage of the reverse parametric modeling method is verified through modeling and error analysis of typical example, which provided a more effective and accurate solution for the parametric modeling based on reverse engineering.
Key words:reverse engineering; division of region; Geomagic Design X; parametric modeling
文章编号:1001-2265(2016)06-0071-04
DOI:10.13462/j.cnki.mmtamt.2016.06.018
收稿日期:2015-07-26
*基金项目:广东省科技计划项目(2011A060901001,2013B061000006,2014A040401078);广州市科技计划项目资助(2013J4300019);广东省研究生教育创新计划项目(2015SFKC23)
作者简介:丛海宸(1991—),男,山东威海人,广东工业大学研究生,研究方向为逆向工程研究,(E-mail)657712928@qq.com。
中图分类号:TH166;TG506
文献标识码:A

