圆角铣削动态切削力方向力系数的时变性研究*
谢黎明,苏彩虹,靳 岚,芮执元
(兰州理工大学 机电工程学院,兰州 730050)
圆角铣削动态切削力方向力系数的时变性研究*
谢黎明,苏彩虹,靳岚,芮执元
(兰州理工大学 机电工程学院,兰州730050)
摘要:针对圆角铣削加工过程切削力不稳定问题,建立考虑再生颤振作用下的圆角铣削动态切削力模型,通过铣削过程中刀具相对于工件坐标的变化,推导切入、切出角随刀具角速度变化的计算公式,研究动态切削力的方向力系数的时变性问题,在仿真得到的颤振稳定性叶瓣图基础上,对圆角铣削在颤振条件下方向力系数的时变性处理的正确性进行验证,并分析了切削力系数及铣刀齿数对颤振稳定性的影响,为圆角铣削切削参数的选择提供了可靠依据。
关键词:圆角铣削;颤振稳定性;动态切削力;方向力系数
0引言
圆角铣削是通过铣刀的圆周进给运动形成圆柱表面的一种铣削工艺,具有加工效率高、工艺使用范围广等优点,因此广泛用于工业生产,特别是汽车工业中。在实际生产中,由于圆角处接触面积大,在没有工件特定长径比以及不考虑丝杠间隙的情况下,刀片通常以顺铣方式,从最大切削厚度处开始切削以降低热量,减少加工淬硬趋势。但是,随着刀具与工件接触面积和进刀径向弧度增加,刀具与工件易产生颤振,造成切削力不稳定。
圆角铣削切削力同时包含切削周期及铣刀绕圆角中心旋转的周期成分。除了周期定向因素随时间的变化,刀齿切入、切出角随时间的变化也增加了其动力学的复杂性。为了解决圆角铣削变切削力及颤振问题,学者们提出了一种圆角铣削颤振时域模型,通过数学建模实现了对圆弧加工中时变切削力和颤振稳定域的预测[1-4]。但是,所建模型是将圆角铣削问题简化为直线铣削,并未体现圆角铣削平均方向力系数的时变性。文献[5]中用最大径向啮合角代替名义径向啮合角推导了平均方向力系数计算公式,虽仿真得到了稳定图形,但未表示出切入切出角在圆角铣削过程的变化规律,建立的模型并不准确。本文在文献[5]所建模型的基础上,以内圆角为研究对象,通过铣削过程中刀具相对于工件坐标位置的变化,推导出顺铣时切入、切出角随刀具角速度变化的计算公式,有效解决动态切削力的方向力系数的时变性问题,对现有的动力学模型进行修正,使其更加准确,并进行仿真,以检测圆角铣削在颤振条件下方向力系数的时变性处理的正确性,同时分析了切削力系数及铣刀齿数对颤振稳定性的影响,为加工参数的选择与优化提供理论依据。
1圆角铣削动态切削力建模
1.1圆角铣削瞬时侵入角变化规律
圆角铣削的几何参数如图1所示[6]。图中以铣刀中心为原点建立局部坐标系,以角中心为原点建立全局坐标系,φ为两坐标系夹角,ae为名义径向切深,θe为刀具与工件的瞬时径向啮合角,ω为铣刀旋转角速度,Ω为圆角进给角速度,W1、W2分别为已加工和待加工圆弧的中心,R1、R2分别为其半径。
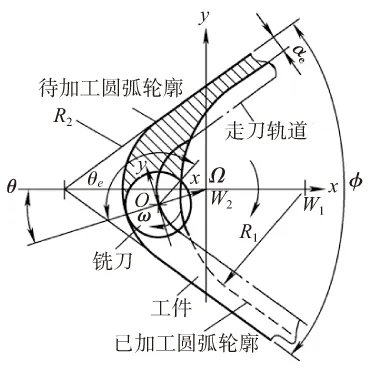
图1 圆角铣削几何参数示意图

图2 轴向、径向切削力示意图
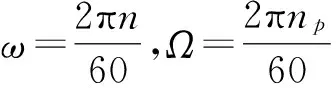
θ(k)=θ0+Ωkt,φ(k)=φ0+ωkt(k=0,1,2…)
(1)
其中θ0和φ0分别为刀具和刀齿的最初位置,从实际切削过程分析可以知道,只有当φst(θ)≤φj(k)≤φex(θ)时,刀具将会在切削区域且刀齿j进行切削,以下建模分析均以此为前提 。
1.2动态切削力模型
铣削时,切削力在X和Y两个方向上对加工系统进行激励,引起的动态位移经过坐标变换作用在刀齿j的切削厚度方向上可以表示为[8]:
h(θ,φj)=ftsinφj+Δxsin(φj+θ)+Δycos(φj+θ)
(2)
式中:ft——每齿进给量;
θ——铣刀中心相对于圆角中心的角位移;
φj——刀齿j的瞬时浸入角;
Δx——刀具与工件x方向动态位移;
Δy——刀具与工件y方向动态位移。

图3 动态切削厚度变化示意图
公式(1)中的切削厚度有两部分构成,一部分是刀具作为刚体运动的静态切削厚度(ftsinφj),另一部分是当前刀齿与前一个刀齿振动引起的动态切削厚度变化,动态切削厚度变化如图3所示。
尽管切削厚度的静态部分在铣削时也发生改变,但由于它与本文所考虑的再生作用无关,故在颤振稳定性分析中可以被忽略,于是可得:
h(θ,φj)=Δxsin(φj+θ)+Δycos(φj+θ)
(3)
设轴向切深为ap,铣刀齿数为n,作用在刀齿j上的切向、径向力为:
(4)
式中:g(θ,φj)——单位阶跃函数;
ktckte——切向、径向切削力系数;
krckre——切向、径向刃口力系数。
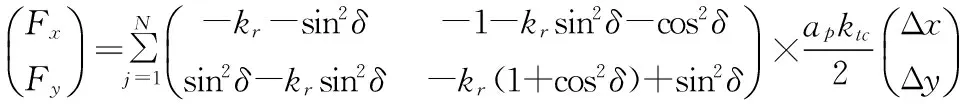
(5)
式中kr=krc/ktc表示为切削力系数与刃口力系数的比例关系,而δ=φj(t)+θ为两齿方向与主轴以及相对于圆形路径的刀具中心定位。将其表示为矩阵形式为:
(6)
式中A(t)——方向力系数矩阵;

假设φp为齿间角,由图2 可知θ=Ωt,φ=ωt,故θ=(Ω/ω)φ,在切削周期T处将方向力系数矩阵进行傅里叶级数展开可得:

(7)
式中
(8)
切入、切出角沿走刀路径的不断改变使平均方向力系数具有时变性,使得用解析法求解圆角铣削颤振稳定域十分复杂。文献[5]中使用最大径向啮合角θemax来代替切入切出角,将直线铣削颤振稳定域解析算法应用于圆角铣削,虽得到了稳定图形,但未表示出切入切出角在圆角铣削过程的变化规律,建立的模型并不符合实际生产。本文通过铣削过程中刀具相对于工件坐标位置的变化,推导出了切入、切出角的计算公式,使圆角铣削的动力学模型更准确。
2切入角与切出角公式推导
在本文中刀齿切入切出角通过刀具与待铣圆槽的相交位置的变化进行推导。假设刀具与待铣圆槽相交点为P(x,y),圆角中心到待铣圆轨迹距离为Rs,铣刀半径为Rc,b1为工件位置坐标的上边界。根据图4所示的位置示意图[3]可得刀具运动轨迹表达式及圆槽轨迹线公式:
(9)

(a) 铣削过程刀具位置示意图
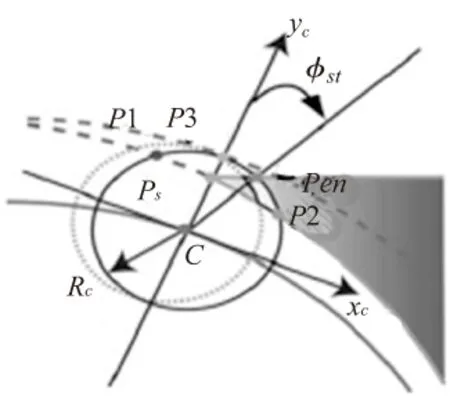
(b) 局部示意图
设刀具初始切入位置为pen(y=b1),根据式(8)可以得到位置坐标为:
(10)
式中:
c1=-2(Rs-Rc)sinθ

x=Ay+B
(11)
将式(9)代入待加工圆槽轨迹线公式得:
即:
a2y2+a1y+a0=0
(12)
式中a2=A2+1,a1=2AB+2Ac,
公式(12)为一元二次方程,求解可以得到两个根,即刀具与待加工圆槽轨迹线相交点p1和p2:
(13)
通过铣削机理可知,在工件上边界外,刀齿不会切削材料,所以在点p1和p3(见图4b)之间切削并未开始,刀齿在p3点处开始进入工件,p2点处切出。点p3及刀齿c位置坐标可以表达为:
(x3,y3)=(Rssinθ,Rscosθ)
(xc,yc)=((Rs-Rc)sinθ,(Rs-Rc)cosθ)
(14)
pen,p3,c三角形可以算出在点pen处切入角:
(15)
式中:
p3,c,p2三角形可以算出切出角:
(16)
式中
点p3,c,p2的位置坐标可以用刀具角度位移变量θ来表示,通过公式(1)中刀具角度位移变量θ的变化公式即可计算出切入角和切出角。
3实验仿真与分析
本文以某厂动梁无滑枕式铣车复合加工中心HMC100S为试验平台进行仿真,该加工中心所用刀架为直驱摆头动力刀架。运用ANSYS软件进行计算和分析得到转速在35~12000r/min运转时[10],对应主轴的频率为0.583~200Hz,动力刀架的前两阶固有频率落在此范围内,当铣刀刀齿的频率等于主轴频率时发生共振。对动力刀架系统取两阶模态,假设X、Y单方向模态相同,其模态参数见表1。

表1 动力刀架系统模态参数
根据上文分析基础上,推导铣削颤振稳定域解析式并利用MATLAB/Simulink搭建仿真模型[11-12],由于实际生产多采用顺铣方式加工,给定切削条件如下:采用带有8个齿的立铣刀顺铣加工灰铸铁工件,切削力系数分别为Ktc=2193.49MPa,Krc=3309.15MPa,Kte=76.33MPa,Ktc=606.68MPa。圆角的几何参数为:Rp=20mm,φ=90°。仿真条件:d=20mm,ae=3mm,νf=3000mm/min-1得到结果如图5~图7所示。

图5 机床的颤振稳定性极限图

图6 铣刀齿数对稳定性的影响

图7 切削系数对稳定性的影响
主轴转速在35r/min到12000r/min范围内,曲线变化频率较大。曲线的下方为稳定区,上方为切削颤振区,所有叶瓣的波谷均位于一条水平线上,该水平线的纵坐标值为最小稳定切深(此处为1.8mm),即当轴向切深小于该值时,在机床性能允许的情况下,无论使用多大的转速加工均不会发生颤振。轴向切深随着转速变大而周期性变化,随着转速提高,变化周期越来越大;在固定其他参数的前提下,轴向极限切削深度与齿数成反比,齿数越多,越容易发成颤振。随着切削力系数的增加,稳定区域变小,最小临界切深略有降低。由此可见,仿真结果与圆角铣削颤振解析算法结果一致。在实际中可以根据稳定性极限图来选择选择相关切削参数,以保证切削正常进行。
4结论
(1)本文建立了考虑再生作用的圆角铣削动态切
削力模型,通过铣削过程中刀具相对于工件坐标位置的变化,推导出了切入、切出角的计算公式,有效解决了动态切削力的方向力系数的时变性问题,对现有模型进行了修正。
(2)用MATLAB进行仿真,得到了铣削加工稳定性叶瓣图,验证了圆角铣削在颤振条件下方向力系数的时变性处理的正确性;分析了铣刀齿数和切削力系数对颤振稳定性的影响。可以看出轴向切深变化周期随着转速提高而增大;在其他参数固定前提下,随着齿数的增多及切削力系数的变大,颤振更易发生。
(3)可以根据本文的仿真结果避开不稳定切深,为圆角铣削过程参数提供了选择范围,进而为消除和避免颤振,用合理加工参数进行生产以提高加工质量及加工效率,提供了比较可靠的依据。
[参考文献]
[1] LI Zhongqun,LIU Qiang. Predication of cutting force for circular corner milling[C].Proceedings of ICMEM2007 International Conference on Mechanical Engineering and Mechanics,November 5-7,2007,Wuxi,China. 2007:1283-1289.
[2] LI Y,LIANG S Y. Cutting force analysis in transient state milling processes[J]. The International Journal of Advanced Manufacturing Technology,1999,15:785-790.
[3] KARDES N,ALTINTAS Y. Mechanics and dynamics of the circular milling process[J]. Journal of Manufacturing Science and Engineering,2007,129:22-31.
[4] BUDAK E,ALTINTAS Y. Analytical prediction of chatter stability in milling-part I:General formulation; Part II:Application to common milling systems[J]. ASME Journal of Dynamic System,Measurement and Control,1998,120:22-36.
[5] 李忠群,刘强.圆角铣削颤振稳定域建模与仿真研究[J].机械工程学报,2010,46(4):181-186.
[6] N Kardes,Y Altintas.Manufacturing Automation Laboratory,University of British Columbia.Mechanics and Dynamics of the Circular Milling Process,2007,120(4):21-31.
[7] LI Zhongqun,LIU Qiang. Solution and analysis of chatter stability for end milling in the time-domain[J]. Chinese Journal of Aeronautics,2008,21(2):169-178.
[8] 刘强,李忠群.数控铣削加工过程仿真与优化——建模、算法与工程应用[M].北京:航空工业出版社,2011.
[9] BUDAK E. Analytical models for high performance milling. Part II :Process dynamics and stability[J].International Journal of Machine Tools & Manufacture,2006,46(12-13):1489-1499.
[10] 陈钦.铣车复合加工中心关键部件静动态分析[D].兰州:兰州理工大学,2014.
[11] 迟玉伦,李郝林.铣削颤振稳定域叶瓣图确定方法研究[J].振动与冲击,2014(4):90-93.
[12] 杨毅青,刘强.数控机床切削稳定性分析及实验研究[J].振动与冲击,2014(10):101-105.
(编辑赵蓉)
Study on the Time Variability of the Directional Milling Coefficients of the Dynamic Cutting Force in the Circular Milling
XIE Li-ming,SU Cai-hong,JIN Lan,RUI Zhi-yuan
(School of Mechanical and Electronical Engineering,Lanzhou University of Technology,Lanzhou 730050,China)
Abstract:Considering of the instability problem of cutting force in circular milling, the dynamics cutting force of circular milling is modeled to include the regenerative effect. The expression of the entry and the exit angles varing with the tool′s angular positions are derived by the change of the tool relative to the workpiece′s postions .Hence the time varing problem of the comesponding average directional force coefficients are effectively solved.the dynamic simulation is developed based on dynamic modeling and stability lobes diagram is abtained and the correctness of the comesponding average directional force coefficients is verified. The influence of cutter tooth number and cutting force coefficient on the chatter stability is studied.As a result, a reliable basis can be provided for the determination of cutting conditions of circular milling.
Key words:circular milling;chatter stability;dynamic cutting force;comesponding force coefficients
文章编号:1001-2265(2016)06-0051-04
DOI:10.13462/j.cnki.mmtamt.2016.06.013
收稿日期:2015-08-04
*基金项目:“高档数控机床与基础制造装备”国家重大科技专项(2010ZX04001-032)
作者简介:谢黎明(1962—),男,回族,安徽黄山人,兰州理工大学教授,研究方向为先进制造技术及数字化技术;通讯作者:苏彩虹(1990—),女,石家庄人,兰州理工大学硕士研究生,研究方向为先进制造技术,(E-mail)sucaihong09112@sina.com。
中图分类号:TH162;TG65
文献标识码:A

