基于博弈分析的网络零售商条件免运费阈值决策研究
宋杰珍,黄有方
(上海海事大学科学研究院,上海市201306)
基于博弈分析的网络零售商条件免运费阈值决策研究
宋杰珍,黄有方
(上海海事大学科学研究院,上海市201306)
摘要:条件免运费(CFS)是网络零售商普遍采用的面向消费者的运费策略之一。针对包含一个网络零售商、一个快递服务商及众多消费者构成的三层供应链,本文首先分析了消费者对条件免运费策略的反应行为,然后分别在分散决策与集中决策模式下求解出了网络零售商免运费阈值的均衡决策。通过两种模式下决策结果的对比,发现网络零售商免运费阈值决策与消费者特征、市场特征及商品特征三类变量有关,且分散决策下网络零售商制定的免运费阈值过高,这使得消费者总购买人次减少了50%,供应链整体期望利润减少了25%。
关键词:斯坦尔伯格博弈;免运费;网络零售;消费者效用
一、引言
近年来,网络零售作为一个重要的销售渠道得到了突飞猛进的发展。网络零售与线下零售的重要区别是网络零售需要对消费者订购的商品进行配送,[1]由此产生的相关费用对网络零售商来说是一笔不小的开支。据估计,一些领域如杂货、玩具等的配送费用可占网络零售商运营成本的30%。[2]虽然向消费者收取运费是补偿配送费用的一种方式,但是收取运费可能会对消费者的购买决策产生极大的负面影响。消费者通常认为网络零售商赚取的利润能够支撑其免运费策略,因此,其运费支付意愿非常低。[3]弗雷斯特研究中心(Forrester Research)的一项调查表明,44%的消费者会在运费结算阶段放弃购物。[4]与此对比,沃克·金沙通信公司(Walker Sands Communication)的调查表明,大约83%的消费者认为免运费是其网上购物的首要原因。[5]由美国联合包裹速递服务公司(UPS)委托互联网信息服务提供商ComScore所做的一份调查也表明,大约80%的消费者认为免运费非常重要。[6]然而,现实中大多数网络零售商却不愿意实施完全免运费,因为这使得他们本来就很低的利润雪上加霜。[7]
鉴于收取运费和完全免运费都是一个两难的选择,很多网络零售商采取了一种折中的方式——条件运费策略或条件免运费策略。条件免运费(Contingent-Free-Shipping,CFS)是一个更加常用的术语,是指仅在消费者购买达到一定的条件(主要包括购买量和购买价值的条件)时才对其免除运费。亚马逊在其运输与配送政策中声明:“如果你购买的商品由亚马逊配送且订单价值达到或超过35美元,那么你就可以享有免运费的权力”。我国最大的网上直销商城——京东商城,也对其注册会员实行购物满79元免运费的策略;如果购买低于79元,需支付5元的固定运费。
条件免运费(CFS)策略使得网络零售商能够平衡运费成本,同时兼顾对消费者的吸引作用。本文考虑快递服务商配送服务批发价格对网络零售商的影响,在供应链的环境下研究网络零售商免运费条件的最优设置。本文的免运费条件特指购买价值条件,即消费者享受免运费的最小购买金额,用免运费阈值(CFS Threshold)表示。
一些学者基于实证研究的方式证明了网络零售商的运费策略能够影响消费者的购买决策[8-11]还有一些学者研究了供给方免运费策略下的购买方订购决策,[12-15]然而这些文献中免运费策略都是外生给定的,未涉及免运费策略的制定。冷(Leng)等[16]2005年在B2B环境下研究了免运费策略的制定,其中,供应方先确定免运费阈值,然后零售商再决定购买数量。虽然该研究基于博弈论的视角研究了免运费阈值决策,但其B2B的环境缺乏终端消费者的反应。冷(Leng)[17]等2010年分析了终端消费者的反应,并在B2C的环境下研究了网络零售商的免运费阈值与产品定价的联合优化,但是没有考虑快递服务商的行为及影响。肖青和王东[18]分析了网络零售商与消费者之间的博弈并在此基础上研究了网络零售商面向多产品配送的免运费阈值决策,但是该研究面对的是网络零售商自营配送的情况。此外,布恩(Boone)和甘尼香(Ganeshan)[19]、阿雷奥拉贝塞利尔(Becerril-arreola)等[20]及江(Jiang)等[21]也研究了网络零售商免运费阈值及其他决策变量的联合优化问题,然而,与冷(Leng)等2010年的研究类似,这些研究都是在假定快递服务商批发价格策略给定的基础上,针对网络零售商单一企业的决策优化。
综上,目前关于免运费策略的研究中,很少在考虑消费者行为基础上通过分析网络零售商与快递服务商之间的相互作用来研究免运费阈值的优化问题。在配送服务外包的情形下,网络零售商免运费阈值决策一方面影响消费者的购买行为,另一方面受其快递服务商批发价格策略的影响。因此有必要从供应链博弈的视角研究三方参与者(网络零售商、快递服务商、消费者)的行为及相互影响,以期对最优免运费策略的制定提供参考。
二、建模及求解
(一)模型背景及假设
在由一个快递服务商、一个网络零售商及众多消费者构成的三级供应链中,消费者向网络零售商下达一个包含一揽子商品的购买订单,然后,网络零售商通过快递服务商向消费者提供订单配送服务。网络零售商向消费者提供条件免运费(CFS)的运费政策,即当消费者实际购买金额达到或超过免运费阈值g时,不用支付配送运费,否则消费者需要支付金额为T的固定运费。考虑到收取运费对消费者需求的负面影响,本文假设网络零售面临的市场需求q(用消费者总购买人次来衡量)与免运费阈值和固定运费线性负相关,且满足关系式q=Q-kg-hT。其中,Q>0是市场潜在需求规模,k>0与h>0分别是市场需求对免运费阈值及对固定运费的敏感系数。网络零售商所售卖商品的平均毛利润率为p,快递服务商单位订单的配送成本为c,快递服务商面向网络零售商制定的单位订单配送服务批发价格为w。用下标r、s分别代表网络零售商及快递服务商,用上标C、D分别代表集中决策与分散决策情形。
为了建模的需要,规定以下假设:
假设1:快递服务商仅基于订单数量向网络零售商收取配送服务费用,即配送服务费用仅与订单数量有关,与订单重量、价值、体积等都无关;该假设在网络零售商所售卖商品价值低、重量小、体积小及没有特殊配送需求时一般是合理的。
假设2:所有参与主体都是理性的。消费者追求自身效用最大化,网络零售商及快递服务商追求利润或期望利润最大化,不存在消费者非理性购买或企业亏本促销的情形。
假设3:供应链中信息是完全的。
假设4:消费者总能找到某种商品组合,使其实际购买金额达到任意一个数值。
假设5:不考虑订单拆分及合并,每人次的购买产生且仅产生单位配送订单。
假设6:为使市场需求不为零,且网络零售商及快递服务商均有利可图,pb>w(b是消费者的最大计划购买金额)及Q-hT>0成立。
在上述模型背景及假设条件的基础上,将分别在网络零售商与快递服务商不同合作模式即分散决策与集中决策两种情形下建立模型,以研究免运费阈值决策的制定。
(二)消费者购买决策分析
在建模之前,有必要对CFS策略对消费者的影响进行分析,以便推算消费者的实际购买金额。
通常情况下,在购物之前消费者都会对本次消费有一个预算。为了与实际购买金额相对应,本文把该预算称为计划购买金额并用变量x来表示。现实生活中,消费者每一次的计划购买金额通常是不同的,为此,本文假设x为区间[0,b](b≥g)上的连续可导的随机变量,且其分布函数为F(x),概率密度函数为f(x)。
用y来代表计划购买金额为x的消费者的实际购买金额,则一个具有代表性的消费者效用函数为:[22]
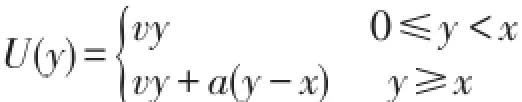
其中,v为实际购买金额不超过计划购买金额时的边际效用,a是超过计划购买金额时的边际效用。根据实际情况,令v>1,0<a<1。可见,U(y)为一个分段递增函数,随着实际购买金额的增加,消费者效用不断增大,但是当购买金额超过计划时,其增速变小。
消费者购买商品的负效用包括支付商品价格带来的负效用和支付运费带来的负效用。假设支付商品价格带来的负效用等于实际购买金额的相反数-y,则不考虑运费时,消费者购买商品的净效用为:

其中,v-1是实际购买金额不超过计划购买金额时的边际净效用,-(1-a)是超出计划购买金额时的边际净效用。由于v>1,0<a<1,所以v-1>0,-(1-a)<0。这说明当消费者实际购买金额不超过购买计划时,消费者增加购买对其是有利的。但是当实际购买金额超过计划时,由于边际净效用小于零,消费者继续购买是不明智的。这也解释了现实中为什么大多数消费者都不愿意超出其购买计划的原因。
根据(1)式,在不考虑运费情况下,消费者实际购买金额等于计划购买金额时其净效用V(y)达到最大。因此,不考虑运费时消费者会刚好购买等于其计划购买金额的商品,即消费者最优的购买金额等于其计划购买金额,y*=x。
然而,考虑运费时,部分消费者由于需要支付运费,因而其净效用会发生一定的变化。这种变化可能导致消费者购买决策的变化。前文已假设消费者支付商品价格带来的负效用为-y。这里相应地假定支付运费带来的负效用为-δT(δ>0),其中,δ是总的负效用(-y-δT)中运费支付所占有的权重。δ越大,消费者支付固定运费T所带来的负效用越大,消费者越不愿意支付运费。因此,可以用来表示消费者对运费的支付意愿。
在CFS策略影响下,消费者的实际购买决策分情况讨论如下:
1.当x≥g时
当x≥g时,网络零售商制定的免运费阈值小于消费者计划购买金额。消费者按照最优购买金额购买时就能满足免运费条件。因此消费者决策不受CFS策略的影响,即消费者不会改变其购买决策,其最优购买金额为y*=x。
2.当x<g时
当x<g时,消费者最优购买金额小于免运费阈值。如果不增加购买量,消费者需要支付固定运费T。因此,此时消费者会权衡是否要增加购买。如果消费者不增加购买(不能享受免运费),消费者实际的净效用为(v-1)x-δT。如果消费者增加购买,由于消费者会购买到等于免运费阈值的购买金额(过多的购买只会带来负效用)。此时消费者实际的净效用为(v-1)x-(1-a)(g-x)。
当(v-1)x-δT≥(v-1)x-(1-a)(g-x),即x<时,消费者不增加购买时的实际净效用大于增加购买时的实际净效用,因此消费者应当选择不增加购买,其最优购买金额y*=x;当时,消费者不增加购买时的净效用小于增加购买时的净效用,因此消费者应增加购买,其最优购买金额y*=g。
综上,可得到命题1。
命题1:当免运费阈值g给定时,计划购买金额为x的消费者的最优购买决策是:
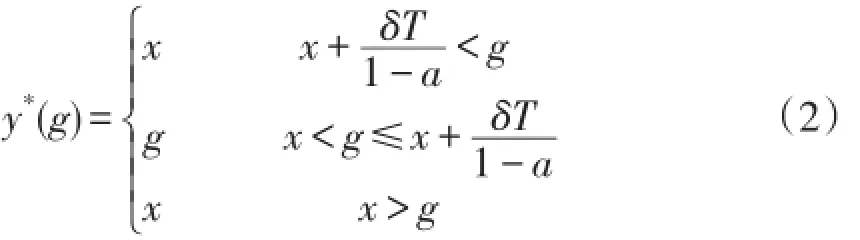
命题1显示,消费者最优购买决策依赖于网络零售商免运费阈值及其自身计划购买金额的大小。当计划购买金额固定时,如果免运费阈值很高,消费者增加购买带来的负效用高于免运费带来的正效用,增加购买的代价较高,因此消费者应当维持原购买计划;如果免运费阈值适中,消费者计划购买金额与免运费阈值比较接近,此时免运费带来的正效用足以弥补增加购买带来的负效用,因此消费者应当增加购买以获得免运费;如果免运费阈值较低,消费者按照原计划购买金额已经享有免运费的权力,而继续购买只会带来负的净效用,因此,消费者应当维持原来的购买计划不变。
由于消费者计划购买金额x∈[0,b],累积分布函数为F(x),概率密度函数为f(x),根据命题1,可以得到消费者实际购买金额的期望值E(y)为:
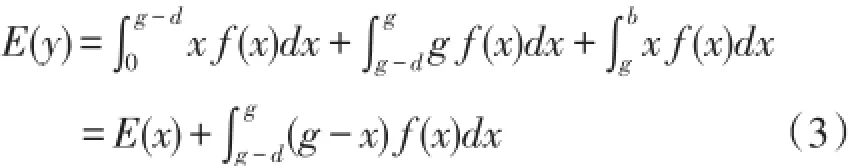
其中,E(x)是随机变量x的均值,代表消费者平均每次的计划购买金额,也可以理解为某次购买时点上多个消费者的平均计划购买金额。
(三)网络零售商与快递服务商分散决策
考虑到消费者的购买决策,理性的网络零售商与快递服务商会依据自身的利益分别进行免运费阈值决策及配送服务批发价格决策。假设快递服务商占据主导地位,首先决定配送服务批发价格w,然后网络零售商再决定免运费阈值g。根据斯坦尔伯格(Stacklberg)博弈模型的求解方法,首先来分析网络零售商的免运费阈值决策。
1.网络零售商的决策
假设网络零售商是风险中性的,则其期望利润函数是:
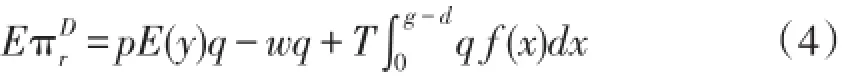
其中,pE(y)q是网络零售商出售商品的期望利润(不含运费);wq是网络零售商向快递服务商支付的运费;T∫0g-dq f(x)dx是网络零售商向购买金额不足免运费阈值的消费者收取的运费。
由于F(x)及f(x)是抽象函数,无法进行进一步的分析,所以需要给出F(x)及f(x)的具体形式。为了简化计算,假定x服从均匀分布,则
把(3)式及q=q0-kg-hT代入,(4)式可重写为:
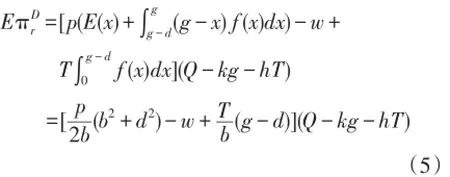
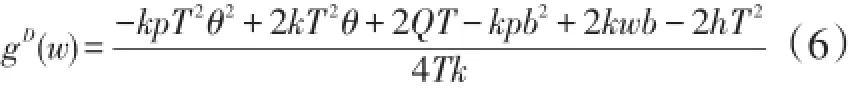
把(6)式代回q=Q-kg-hT及(4)式,可以得到在给定的配送服务批发价格下,市场需求及网络零售商的期望利润是:
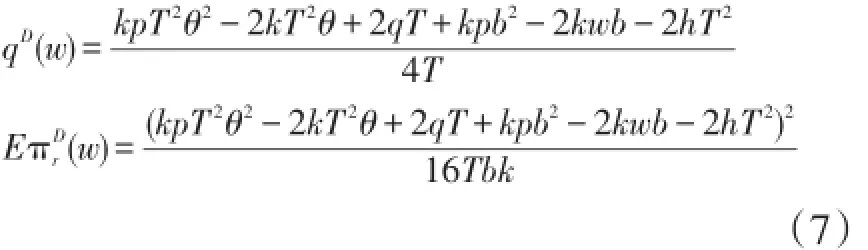
2.快递服务商的决策
快递服务商的期望利润函数是:
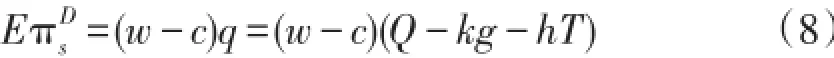
把(6)式代入(8)式,得到:
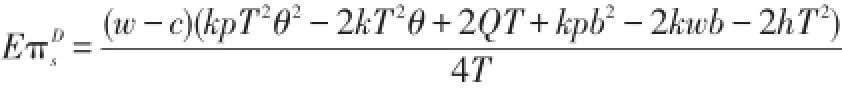
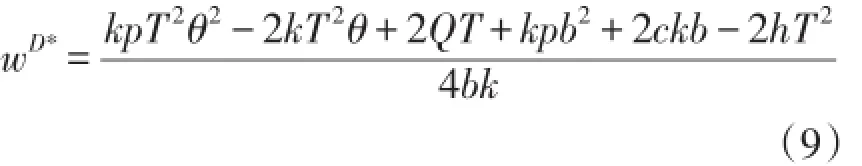
把(9)式代入(6)式,得到分散决策下的最优免运费阈值为:
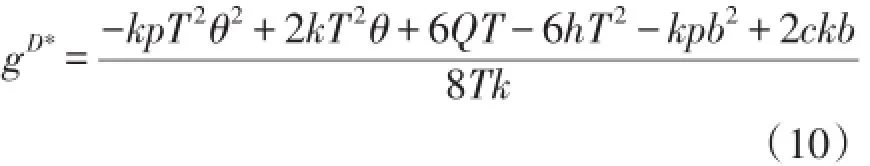
(四)网络零售商与快递服务商集中决策
集中决策类似于网络零售商自营配送或有一个虚拟决策主体对双方决策进行协调。把(5)和(8)两式相加,得到决策主体的期望利润函数是:
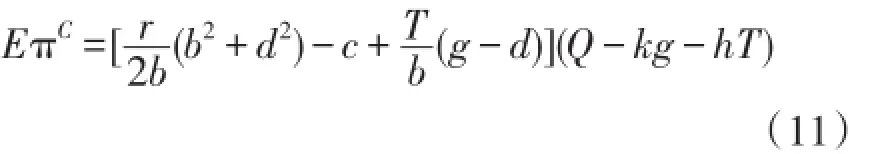
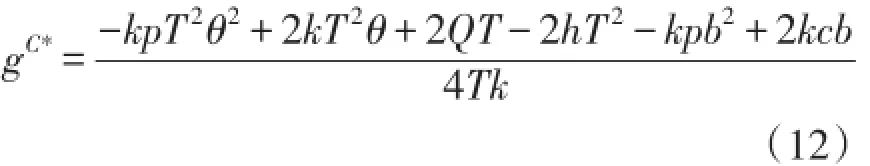
三、分散决策与集中决策的对比分析
通过对分散决策下的(10)式以及集中决策下的(12)式求偏导,可以得到:
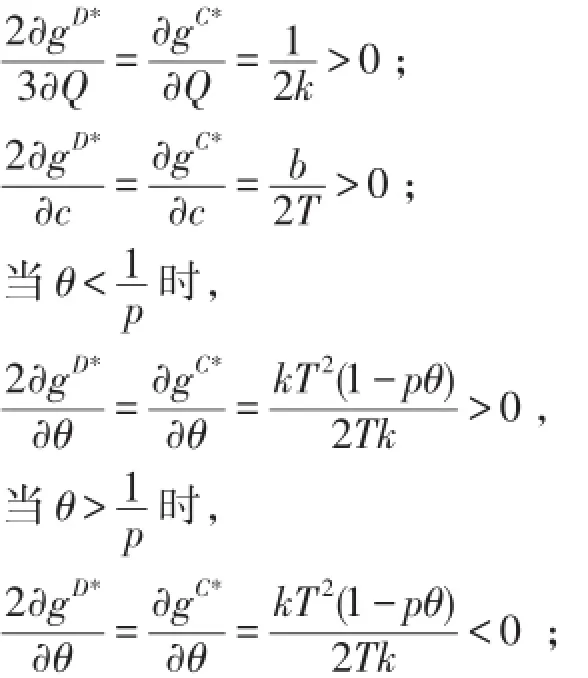

因此可以得到命题2。
命题2:最优免运费阈值具有下述性质:与市场潜在需求规模成正比;与单位配送成本成正比;当消费者运费支付意愿较高时,与支付意愿成反比;当运费支付意愿较低时,与支付意愿成正比;与商品的平均毛利润率及消费者平均计划购买金额成反比;与市场需求对免运费阈值和对固定运费的敏感系数成反比。
该命题从直观上很容易得到解释,且与经营实践相符。
当市场潜在需求规模较大时,网络零售商通过收取运费获得的收益大于降低免运费阈值吸引消费者获得的收益,因此提高免运费阈值是有利的。现实中经常可以看到一些处于起步阶段的网络零售商利用运费促销甚至完全免运费吸引消费者,提高消费者总购买人次。随着企业的发展,潜在市场需求规模增大,降低免运费阈值以提高市场需求的策略不再占优,相反提高免运费阈值却可以获得不菲的运费收益,因此有的企业会提高免运费阈值。例如,针对重点城市当当网最早全场无限额免运费,2008年后把免运费阈值改成20元,2014年又涨到39元。
免运费阈值通常会随着配送成本的增加而增加以弥补相关支出。生鲜产品的配送成本比普通产品较高,所以很多网络零售商针对生鲜产品的免运费阈值通常高于普通产品,如1号店超市2016年针对普通产品68元免运费,但是生鲜产品99元免运费。
当消费者运费支付意愿较高(对应较低的δ及较小的θ值)时,免运费促销的推动作用较小,网络零售商要增加利润必须考虑免运费阈值对市场需求的影响。由于市场需求与免运费阈值成反比,所以消费者运费支付意愿越高,网络零售商越应当降低免运费阈值以刺激需求来提高利润。消费者运费支付意愿较低时的分析与此类似。从现实来看,目前我国消费者的总体支付意愿处于较低的水平,但是由于消费者收入的增加及购物理性的增强,消费者的支付意愿具有逐渐上升的趋势,因此很多购物网站的免运费阈值也是逐渐增加的。当当网在2014年将甘肃、新疆、西藏等地区的免运费标准由29元调整至99元,不足99元订单将收取5元运费。虽然这有可能是市场潜在需求规模、成本等因素的影响,但是消费者运费支付意愿的提高也是一个不可忽视的因素。
消费者最大计划购买金额较大及商品利润率较高,都意味着网络零售商盈利水平较高,一般来说,盈利水平较高的企业能够承担较高的运费成本,通常都会实施较为宽松的运费政策,即免运费阈值较低或完全免运费。例如,售卖高档珠宝的网络零售商钻石小鸟对消费者实行完全免运费的策略。
最后,市场需求对免运费阈值或对固定运费越敏感,免运费阈值或固定运费每增加1单位导致消费者总购买人次减少得越多,企业提高免运费阈值的损失就越大。因此,理性的网络零售商不会提高免运费阈值。当产品进行降价促销时,消费者通常关注商品降价带来的效用,对免运费阈值的敏感性降低,因此销售折扣商品的网络零售商如唯品会等大都设置比其他网络零售商要高的免运费阈值。
接下来把不同情形下的免运费阈值决策及供应链绩效进行比较以考察不同合作模式的影响。
首先,把(6)式及(12)式进行对比,可以发现由于c<w,因此gC*<gD*。
进一步,把(10)式及(12)式分别代入q=Q-kg-hT,得到分散决策与集中决策下的市场需求分别为:
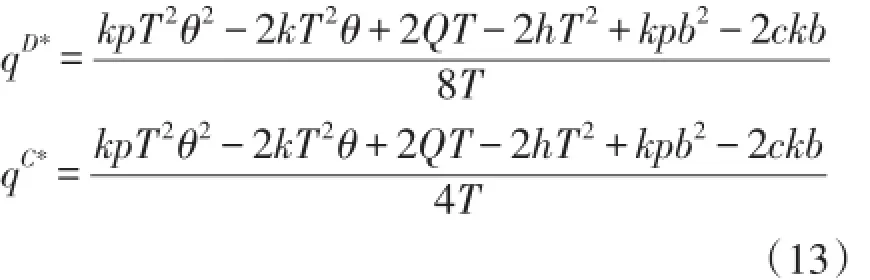
把(9)式及(10)式分别代入(5)式和(8)式,得到分散决策下网络零售商的期望利润、快递服务商的期望利润及供应链整体的期望利润分别为:

把(12)式代入(11)式,得到集中决策下的供应链整体期望利润为:
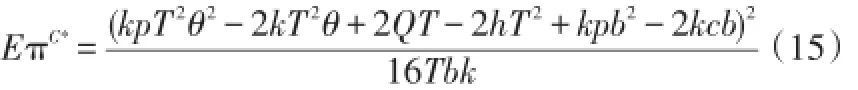
命题3:与集中决策相比,在分散决策情形下,网络零售商倾向于制定较高的免运费阈值,这使得市场需求(消费者总购买人次)减少了50%,并使得供应链整体期望利润降低了25%。
四、案例应用
这里以当当网为案例背景对前述结论进行解释与验证。相关数据来源于当当网年报、新闻报道及专家调查,商品范围仅限于自营书籍。当当网在A地区与某快递服务商进行配送服务合作,该地区潜在的市场需求规模为Q=600万(人次)。当当网的商品平均毛利润率(不含运费)为r=6.8%,并规定未达到免运费阈值时,消费者需要支付固定运费T=5(元)。市场需求对免运费阀值的敏感系数为k=60 000(人次),对固定运费的敏感系数是h=10 000(人次)。在消费者负效用中,运费的相对权重是δ=2,消费者计划购买金额服从均匀分布,且x∈[0,180],最大购买金额b=180元,超出购买计划时,消费者边际效用系数a=0.5。该快递服务商单位订单的配送成本为c=4元。
根据公式(10)、(12)~(15),得到分散决策与集中决策下的供应链决策及绩效如表1所示。
当当网目前的免运费阈值为49元,与分散决策下的59.615元比较接近。考虑到基本数据误差的影响,该阈值在分散决策模式下基本合理或可适度降低。
通过表1可以发现,分散决策下的免运费阈值高于集中决策下的免运费阈值,市场需求减少了50%,供应链整体期望利润减少了25%。因此,如果当当网能够与快递服务商进行集中决策,免运费阈值可以进一步降低。
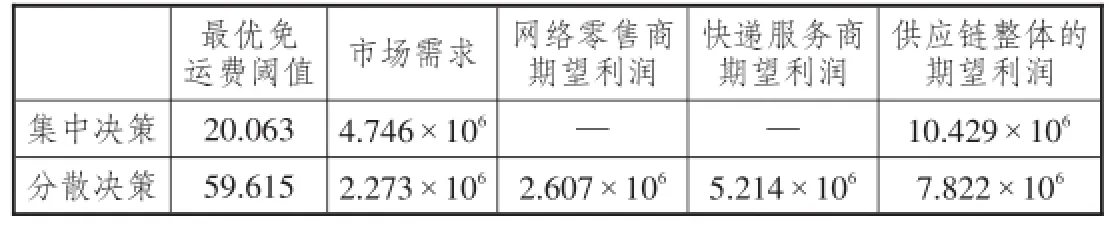
表1 集中决策与分散决策下的供应链决策及绩效
接下来对最优免运费阈值决策进行敏感性分析,以期对最优免运费阈值的性质(命题2)进行验证,并对当当网在外部环境变化时的运费政策调整提供一定的参考。
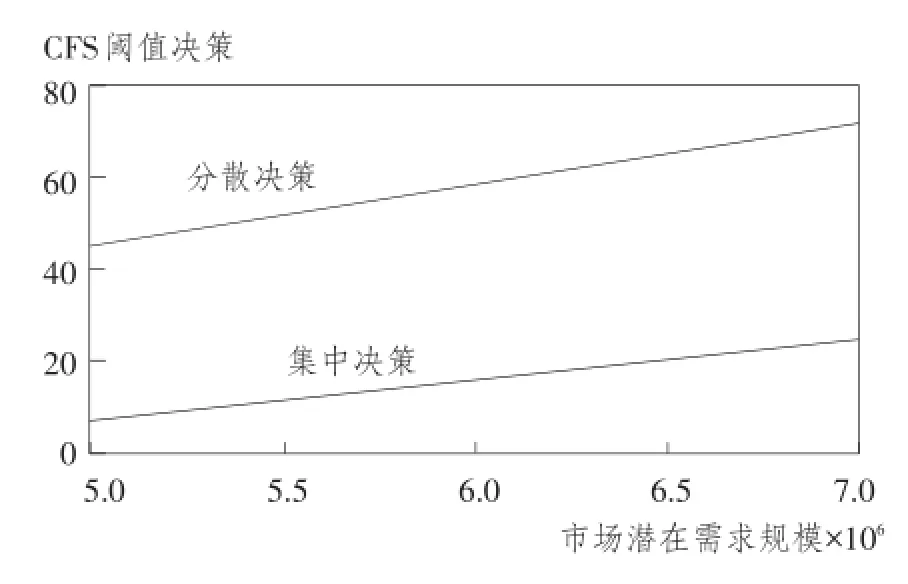
图1 CFS阈值决策与市场潜在需求规模的关系
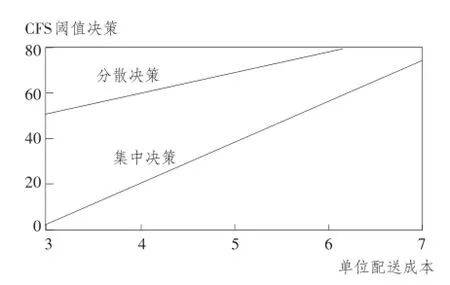
图2 CFS阈值决策与单位配送成本的关系

图3 CFS阈值决策与消费者运费支付意愿的关系

图4 CFS阈值决策与市场需求对免运费阈值敏感系数的关系
在图1中,假设市场潜在需求规模Q在500万元至700万元之间变化。在图2中,假设单位订单配送成本c在3元到6元之间变化。由图1和图2可以看出,最优免运费阈值与潜在市场需求规模和单位订单配送成本都成正比。
在图3中,当消费者运费支付意愿1/δ较大时,最优的免运费阈值与δ成正比。一旦运费支付意愿1/δ低于(δ超过7.353),最优的免运费阈值会随着支付意愿的降低(δ值的增加)而降低。
在图4和图5中,令市场需求对免运费阈值和对固定运费的敏感系数分别在50 000 到70 000和5 000到50 000之间变化,可以发现,市场需求对这两个变量的敏感性越高,最优的免运费阈值应当越低。
图6和图7分别显示了消费者最大计划购买金额b在140元至240元之间变化,以及商品平均毛利润率p在6%至10%之间变化时最优免运费阈值的变化情况,可以看出,最优的免运费阈值与消费者最大计划购买金额(在本文中也对应着消费者的平均计划购买金额)及商品平均毛利润率成反比。
五、结束语
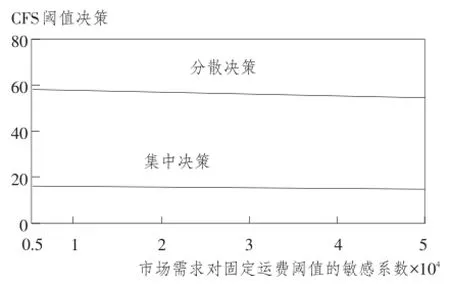
图5 CFS阈值决策与市场需求对固定运费敏感系数的关系
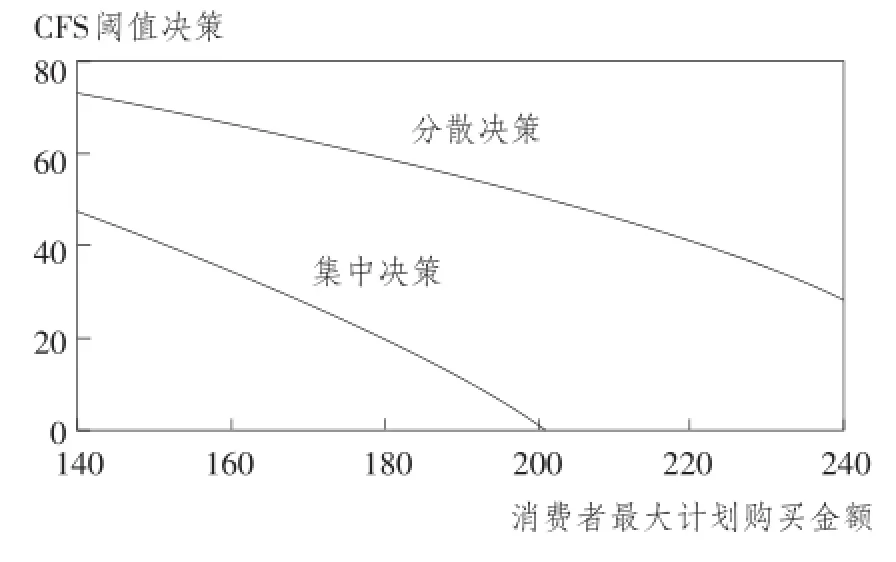
图6 CFS阈值决策与消费者最大计划购买金额的关系
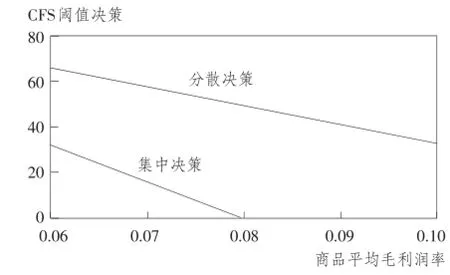
图7 CFS阈值决策与商品平均毛利润率的关系
条件免运费(CFS)是常见的网络零售商促销策略之一。本文基于博弈论研究了网络零售环境下CFS阈值的优化问题,除了从理论上得到CFS阈值的解析解及相关性质之外,还结合企业经营的实践对相关结论进行了解释和验证。
本文的研究成果至少可以为网络零售商环境下CFS策略的优化提供两点启示。首先,CFS策略的优化要全面考虑与消费者相关的特征变量(消费者对运费的支付意愿、消费者的计划购买金额)、与市场相关的特征变量(潜在市场需求规模、市场需求对免运费阈值和固定运费的敏感系数)及与商品相关的特征变量(平均毛利润率及单位配送成本),所有这些变量使得销售不同商品的不同网络零售商甚至相同零售商在不同经营时期的最优免运费阈值都不一样。其次,CFS策略的优化要考虑网络零售商和快递服务商之间的相互作用。双方的合作模式(集中决策还是分散决策)对最优的CFS阈值有巨大影响。为了提高供应链整体及单个企业的期望利润,分散决策下网络零售商与快递服务商应对免运费阈值进行协调优化。
为了便于求解及分析,本文在模型背景及假设中做了一些简化。未来更加深入的研究包括但不限于:第一,考虑两个网络零售商竞争的情形;第二,考虑消费者计划购买金额的其他分布形式如正态分布等;第三,考虑配送成本及配送服务批发价格与商品价值相关的情形;第四,研究分散决策下网络零售商与快递服务商的协调机制。
参考文献:
[1]Gümüs Mehmet,Li Shanling,Oh Wonseok,et al.Shipping fees or shipping free?a tale of two price partitioning strategies in online retailing[J].Production and operations management,2013(4):758-776.
[2]BARSH J,CRAWFORD B,GROSSO C.How E-tailing can rise from the ashes[J].The mckinsey quarterly,2000 (3):98-109.
[3]Goethals Frank,Leclercq-vandelannoitte Aurelie,Tutuncu Yazgi.French consumers'perceptions of the unattended delivery model for e-grocery retailing[J].Journal of retailing and consumer services,2012(1):133-139.
[4]SUCHARITA M.The state of retailing online 2009:profitability,economy,and multichannel[R].Forrester Research,2009.
[5]Walker Sands.Reinventing retail:What businesses need to know for 2015[R/OL].http://www.walkersands.com/pdf/2015 _future-of-retail.pdf .
[6]Com Score.UPS Pulse of the Online Shopper[R/OL].http://thenewlogistics.ups.com/retail/comscorestudy/documents/UP S_com Score_Whitepaper_2014.pdf.
[7]Forrester Research.Smarter strategies for free shipping[R/OL].https://www.ups.com/media/en/Smarter_Strategies_for_Free_Shipping.pdf.
[8]Schindler ROBERT-M,Morrin MAUREEN,Bechwati NADA-NASR.Shipping charges and shipping-charge skepticism:implications for direct marketer's pricing formats[J].Journal of interactive marketing,2005(1):41-53.
[9]LEWIS M.The effect of shipping fees on customer acquisition,customer retention,and purchase quantities[J].Journal of retailing,2006(1):13-23.
[10]LEWIS M,SINGH V,FAY S.An empirical study of the impact of nonlinear shipping and handling fees on purchase incidence and expenditure decisions[J].Marketing science,2006(25):51-64.
[11]Huang Wen-Hsien,Cheng Yi-Ching.Threshold free shipping policies for internet shoppers[J].Transportation research part A,2015(82):193-203.
[12]Zhou Bin,Katehakis Michael-N,Zhao Yao.Managing stochastic inventory systems with free shipping option[J].European journal of operational research,2009(1):186-197.
[13]HUA G W,WANG S Y,CHENG T C E.Optimal order lot sizing and pricing with free shipping[J].European journal of operational research,2012(2):435-441.
[14]周永圣,王磊,何明珂.供应商免费送货条件下零售商的订货策略选择研究[J].系统科学与数学,2012(3):288-296.
[15]Kwon Kysang,Cheong Taesu.A minimax distribution-free procedure for a newsvendor problem with free shipping[J].European journal of operational research,2014(1):234-240.
[16]Leng M,Parlar M.Free shipping and purchasing decisions in B2B transactions:A game-theoretic analysis[J].IIE trans,2005(37):1119-1128.
[17]LENG M,BECERRIL-ARREOLA R.Joint pricing and contingent free-shipping decisions in B2C transactions[J].Production and operations management,2010(4):390-405.
[18]肖青,王东.网上零售业多产品配送服务定价研究[J].计算机应用研究,2013(9):2619-2621.
[19]Boone Tonya,Ganeshan Ram.Exploratory analysis of free shipping policies of online retailers[J].International journal of production economics,2013(2):627-632.
[20]Becerril-arreola Rafael,Leng Mingming,Parlar Mahmut.Online retailers' promotional pricing,free-shipping threshold,and inventory decisions:A simulation-based analysis[J].European journal of operational research,2013 (2):272-283.
[21]Jiang Yuanchun,Shang Jennifer,Liu Yezheng.Optimizing shipping-fee schedules to maximize e-tailer profits[J].Int.J.Production Economics,2013(146):635-645.
[22]Khouja Moutaz,Pan Jingming,Ratchford Brian-T,Zhou Jin.Analysis of free gift card program effectiveness[J].Journal of retailing,2011(4):444-461.
责任编辑:方程
Decision on Contingent-Free-Shipping Threshold for E-retailers based on Game Analysis
SONG Jie-zhen and HUANG You-fang
(Shanghai Maritime University,Shanghai201306,China)
Abstract:Contingent-Free-Shipping(CFS)is a prevalent strategy offered to consumers adopted by e-retailers.In a threelevel supply chain containing one e-retailer,one courier service provider and quantity of consumers,the responsive behavior of a representative consumer to the CFS policy is analyzed.Then it solves out the equilibrium strategies about how the retailer deciding the CFS threshold value under decentralized and centralized cases.By comparison of the strategies under the two cases,it is found that the optimal CFS thresholds are relevant to the attributes of consumers,market demand and the commodity.Besides,in the decentralized case the e-retailer tends to set a higher threshold value,resulting in the total demand dropped by 50%and the expected profit of the entire supply chain decreased by 25%.
Key words:Stackelberg game;free shipping;online retailing;consumer utility
中图分类号:F274
文献标识码:A
文章编号:1007-8266(2016)07-0033-09
收稿日期:2016-05-16
作者简介:宋杰珍(1980—),女,湖北省襄阳市人,上海海事大学科学研究院博士生,主要研究方向为供应链协调管理;黄有方(1959—),男,浙江省新昌县人,上海海事大学科学研究院教授,博导,博士,主要研究方向为物流管理与工程。

