基于小波分析的大坝监测数据处理

崔 伟 杰,　李　饶,　张 学 峰

(1.雅砻江流域水电开发有限公司，四川 成都　610000;2.德阳市水务局，四川 德阳　618000)

基于小波分析的大坝监测数据处理

崔 伟 杰1,李饶1,张 学 峰2

(1.雅砻江流域水电开发有限公司，四川 成都610000;2.德阳市水务局，四川 德阳618000)

摘要：大坝监测系统所采集的监测数据资料存在异常值并受噪声的影响，小波分析具有多分辨率、时频分析的特点。小波分析方法能准确、迅速的定位监测数据序列中异常值，适合运用于数据较多的情况。利用点的小波变换模极大值和阈值法能有效的去除异常值，避免人工去除的繁琐过程。对去除异常值后的序列进行小波软阈值去噪，消除监测数据中噪声的影响，为后续监测资料分析评价提供能反映大坝真实性态的数据。同时该方法适应性较广，能运用到其他数据预处理中，但必须根据实际情况选择合适的小波函数以及阈值。

关键词：小波分析；异常值检测；实例分析；大坝监测数据

0引言

由于受监测环境、监测位置、测试人员等的影响，大坝监测设施所测得的数据不可避免的存在误差，并且受噪声的影响。其中由于观测错误引起的误差称为粗差，含粗差的测值称为异常值[1]。噪声以及异常值的存在会影响监测数据的真实性，对不真实的数据进行分析一定程度上会产生不可靠的评价。因此，去除监测数据中的异常值以及消除噪声对监测数据的影响具有重要意义。徐洪钟的《基于小波分析的大坝观测数据异常值检测》[2]提出利用小波分析检测监测数据中的异常值，但并没有提出如何去除数据中异常值以及如何消去噪声影响。小波分析具有空间局部化、多分辨率分析的特点，监测数据中的异常值可以看作信号的奇异点，通过跟踪小波变换的模极大曲线确定奇异点的位置，而奇异点的奇异性强弱可由小波变换的模极大值来刻画，然后利用阈值法去除监测数据中的异常值[3]。对去除异常值后的监测数据序列，利用小波软阈值去噪法进行去噪处理，最后根据处理后的小波系数重构原信号，达到去除异常值以及消噪的目的。为后续分析评价提供真实的数据资料。

1小波分析

1.1小波变换

(1)

(2)

称为f(t)的小波变换。其中a为尺度因子，b为位移因子。

若f(t)为连续函数或信号，小波基函数ψa,b(t)的两个参数a和b均为连续变量，且ψ(t)满足容许性条件，则连续小波变换的逆变换存在，形式如下：

(3)

1.2信号奇异性

若函数在某处有间断或某阶导数不连续，则称该函数在此处有奇异性。信号的奇异性包含了信号的本质信息。函数的局部正则性常用Lipschitz指数度量[4]。

定义1：如果存在常数Kv>0和[α]次多项式pv，使得

∀t∈R,|f(t)-pv|≤Kv|t-v|α

(4)

称函数r在点v∈R为Lipschitzα(α≥0)。

定义2：设f(x)∈L2(R)，若f(x)对∀x∈δx0，小波函数ψ(x)是实函数且连续可微，并具有n阶消失矩(n∈Z+)，则有|Wf(s,x)|≤Ksα。K为常数，则称α为x0点的Lipschitz指数。

设θ(x)是一个光滑函数，小波函数ψ(x)是θ(x)的一阶单数，即ψ(x)=dθ(x)/dt，则f的连续小波变换为

(5)

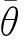
1.3异常值去除及去噪

监测数据序列信号用其多分辨分析子空间V0表示，则有

V0=V1⊕W1=V2⊕W2⊕W2=…=Vd⊕Wd-1⊕Wd-2⊕…⊕W2⊕W1

(6)

其中Vi为小波分解后信号的低频部分，Wi为小波分解后信号的高频部分(i=1,2,…,d)；d为分解的层数。

在大坝监测数据序列中，异常值以及噪声引起的数据一般分布在高频部分，对小波分解后的高频部分进行处理，可达到去除异常值以及噪声影响的目的，将处理后的高频系数与低频系数重构，可得处理后的监测数据序列。

有些异常值可能是由水位、温度、降雨等环境量变化引起的，因此，要对这些值进行判别[6]：利用小波分析锁定数据中可能的异常值，再利用逐步回归模型对监测数据序列进行回归分析，计算实测值与拟合值残差序列的标准差σ，根据拉依达准则，随机误差超出±3σ的概率极小，对可能是异常值的残差就行检验，未超出±3σ，则可认为是环境因素引起变化的正常值；反之则为异常值，需进行剔除。

本文利用阈值法去除异常值，这一过程与硬阈值去噪相反：

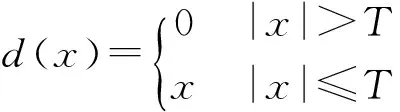
(7)

式中，T为所选阈值。即将大于给定阈值的高频系数定为零，保留小于给定阈值的高频系数，这里阈值的选取跟正常值分解的高频系数范围有关，应接近正常值分解的高频系数上限，这样既能去除异常值又使对正常值的影响降到最小。

对去除异常值的监测数据序列进行软阈值去噪：

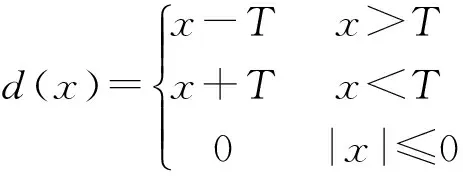
(8)

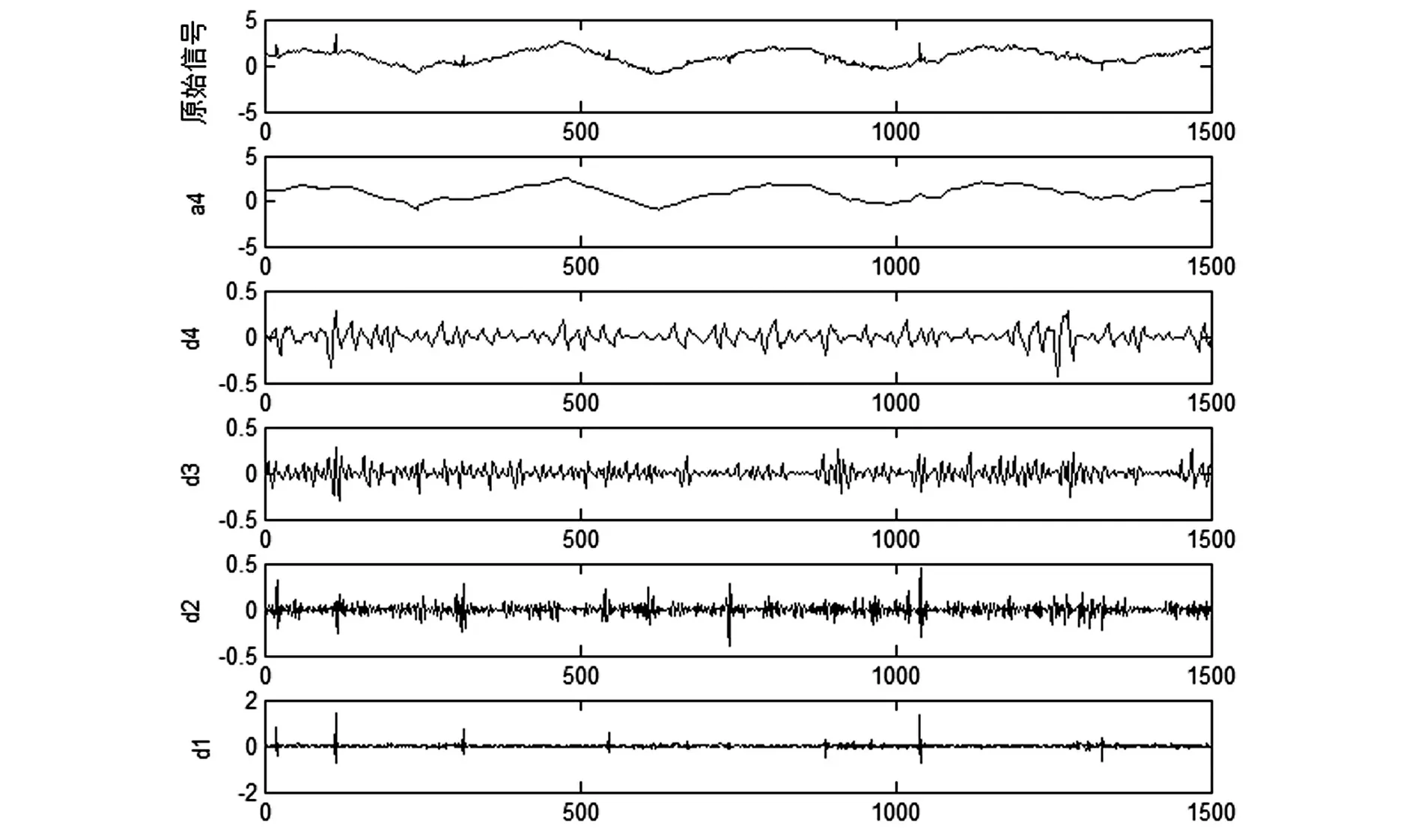
图1　db2小波分解序列图

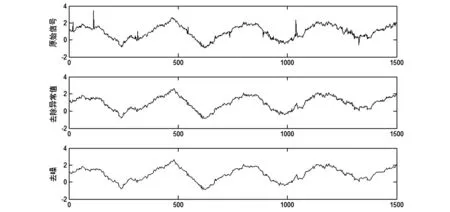
图2　小波分析处理数据效果对比图

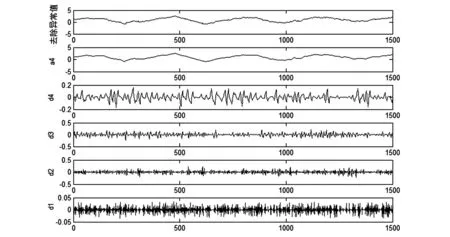
图3　去除异常值后小波分解序列图

此处阈值的选取要根据信号的相对平稳性以及信噪比的大小而定，对于平稳性较差的信号，阈值应选得小一些；同一信号，信噪比大时，噪声功率小，阈值应选得小一些[7]。

2实例分析

选取某混凝土坝变形监测P3测点自2010年9月1日到2014年10月9日共1500组数据，一般较小尺度下的小波变换能减小频率混叠现象，这里选用正则性较好的db2小波对该序列进行4层分解，分解的结果如图1所示，其中d1、d2、d3、d4为序列的高频部分，a1为序列的低频部分。

由图1可知，高频部分d1在t=19、t=113、t=315、t=545、t=889、t=1039以及t=1327处有可传播的模极大值点。高频部分d2在t=736处有模极大值点。高频部分d1和d2还存在一些幅值不大数量较多的模极值点，其奇异性是由噪声引起的。对该监测序列建立逐步回归模型，对上述异常点进行检验，发现以上8个点的实测值与拟合值的残差均超过±3σ，说明这几个点均为异常点。利用式(7)，选用合适的阈值，分别对高频部分进行处理，去除异常值。去除效果与原始数据对比图见图2所示。

绘制去除异常值后的小波分解序列图，如图3所示。从图中可以看出，高频部分受噪声影响较大，波动较剧烈。利用式(8)，选用合适的阈值，对去除异常值的高频序列进行去噪处理。处理后监测序列与原始监测序列对比如图2所示。

由图2可知，监测数据经过小波阈值处理后，能较好的消除异常值，原始序列未出现明显变化，保留了监测数据序列变化趋势。由图2、图3可知，软阈值去噪法去噪效果较好，能有效的消除序列中噪声影响，使监测数据序列更加光滑、失真小。

3结论

大坝监测系统所采集的监测数据资料存在异常值并受噪声的影响，小波分析具有多分辨率、时频分析的特点。小波分析方法能准确、迅速的定位监测数据序列中异常值，适合运用于数据较多的情况。利用点的小波变换模极大值和阈值法能有效的去除异常值，避免人工去除的繁琐过程。对去除异常值后的序列进行小波软阈值去噪，消除监测数据中噪声的影响，为后续监测资料分析评价提供能反映大坝真实性态的数据。同时该方法适应性较广，能运用到其他数据预处理中，但必须根据实际情况选择合适的小波函数以及阈值。

参考文献：

[1]何金平. 大坝安全监测理论与应用[M]. 中国水利水电出版社, 2010.

[2]徐洪钟, 吴中如, 李雪红,等. 基于小波分析的大坝观测数据异常值检测[J]. 水电能源科学, 2002(4):20-21.

[3]潘泉. 小波滤波方法及应用[M]. 清华大学出版社, 2005.

[4]孙延奎. 小波分析及其应用[M]. 机械工业出版社, 2005.

[5]何浩祥, 孙立, 闫维明,等. 基于小波分析的结构损伤信号奇异性检测[J]. 工业建筑, 2007, 37(S1):204-207.

[6]袁晓峰. 大坝安全监测资料分析若干问题研究——万安电厂典型坝段监测资料分析[D]. 南昌大学, 2007.

[7]张德丰. 基于小波的信号阈值去噪算法研究[J]. 现代计算机：专业版, 2007(5):26-28.

收稿日期:2016-05-25

中图分类号:TV42+1.1；X830.3

文献标识码:A

文章编号:1001-2184(2016)03-0109-03

作者简介:

崔伟杰(1988-)，男，河北石家庄人，毕业于河海大学水工结构工程专业，现于雅砻江流域水电开发有限公司从事项目管理工作；

李饶(1988-)，男，四川资阳人，毕业于四川大学水工结构工程；现于雅砻江流域水电开发有限公司从事项目管理工作；

张学峰(1986-)，女，山西文水人，毕业于河海大学水工结构工程专业，现于德阳市水务局从事党建党务人事管理工作.

(责任编辑：卓政昌)