基于高斯混合模型的说话人识别研究
朱宇轩
(西华大学,四川 成都 610039)
基于高斯混合模型的说话人识别研究
朱宇轩
(西华大学,四川 成都 610039)
摘要:说话人识别本质上是一个模式识别问题,而模式识别系统的目标是要在表示空间和解释空间之间找到一种映射关系。高斯分布又称为正态分布,是一个在数学、物理及工程领域都非常重要的连续分布函数,它描述了一种围绕某个单值聚集分布的随机变量。
关键词:高斯分布;随机变量
1引言
在实际生活中,许多物理现象以及各种心理学测试分数都近似地服从高斯分布。在统计学以及许多统计测试中高斯分布也是应用最广泛的一类分布。高斯混合模型(Gaussian Mixture Model,GMM)是单一高斯密度函数的扩展,由于高斯混合模型可以逼近任意形状的概率密度分布,所以高斯混合模型被广泛的运用到各种领域,如语音识别,图像识别等,并取得了理想的效果。
2GMM模型基本概念
GMM混合模型可以看作一种状态数为1的连续分布的隐马尔可夫模型CDHMM。它是用M个单高斯分布的线性组合来描述帧特征在特征空间中的分布。一个M阶的混合高斯模型的概率密度函数可以由M个单高斯概率密度函数加权和得到,其表达式如下:
(1)
式中:X是一个D维随机向量;M是混合模型的阶数;ωi,i=1,…,M是混合权重,且其满足以下条件:
(2)
bi(X),i=1,2,…,M是子分布,每个子分布是D维的联合高斯概率分布,可表示为:
(3)
式中,μi是均值向量,Σi是协方差矩阵。
整个高斯混合模型可以通过参数均值向量、协方差矩阵和混合权重来描述。所以高斯模型λ可以表示为:
λ={ωi,μi,∑i},i=1,…M
(4)
3GMM模型的训练
GMM模型的训练就是给定一组训练数据,依据某种准则确定模型的参数。最常用的参数估计方法是最大似然(Mxaimum Likehhood,简称为ML)估计。最大似然估计是把待估计的量看成固定但未知的量,然后求出能够使学习样本出现概率最大的参数值,并把它作为参数的估值。GMM模型参数的初始化有两种不同的方法:第一种是使用一个与说话人无关的HMM模型对训练数据进行自动分段。训练数据语音帧根据其特征分到M个不同的类中(M为混合高斯分量的个数),与初始的M个高斯分量相对应。每个类的均值和方差作为模型的初始化参数。第二种方法从训练数据序列中随机选择M个矢量作为模型的初始化参数。尽管有实验证明EM算法对于初始化参数的选择并不敏感,但是第一种方法训练要优于第二种方法。
另外由于条件的限制,通常得不到充分语音数据对模型参数进行训练。GMM模型的协方差矩阵的一些分量可能会很小,这些很小的值对模型参数的似然对函数影响很大,严重影响系统的性能。为了避免小的值对系统性能的影响,在EM算法的迭代计算中,可以对协方差的值设置一个门限值,在训练过程中令协方差的值不小于设定的门限值。门限值设置可通过观察协方差矩阵来定,一般情况下,决大多数值都大于0.0001。只有极少数值在这个范围之外,为此,可将门限值设置为0.001。
4GMM模型的识别
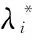
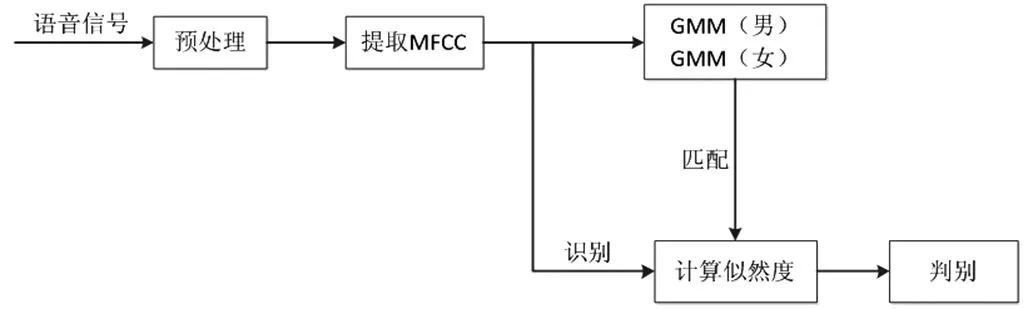
图1 GMM模型的说话人性别识别系统结构框图
根据贝叶斯理论,最大后验概率可表示为:
(5)
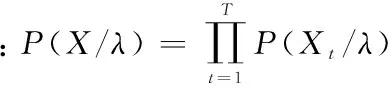
(6)
其对数形式为:
(7)
由于P(λt)的先验概率未知,我们假定该语音信号被判别为男声和女声的可能性相等,即:
(8)
对于一个确定的观察值矢量X,P(X)是一个确定的常数值,对男声和女声模板相等。因此求取后验概率的最大值可以通过求取P(X/λi)获得,所以识别该语音是男声还是女声可以表示为:
i*=argmaxP(X/λi),i=1,2
(9)
式中:i*即为识别出的说话人性别最大概率。
5总结
考虑到高斯函数对真实数据的较好描述,另外由于高斯函数的线性组合仍然是高斯函数,而且在理论上任意形式的总体分布都可以用若干个高斯函数的混合来逼近。所以采用高斯混合函数来估计语音特征的概率分布,这样就得到了说话人的高斯混合模型。
参考文献:
[1]吴朝晖,杨莹春. 说话人识别模型与方法[M].北京:电子工业出版社,1995.
[2]邓英, 欧贵文.基于HMM的性别识别[J].计算机工程与应用, 40(15): 74-75.
作者简介:朱宇轩,性别:男,民族:汉族,籍贯: 四川南充,职务:工人,学历:大学本科,单位:西华大学,研究方向:电子,计算机。
中图分类号:TN915
文献标志码:A
文章编号:1671-1602(2016)12-0136-01

