ANFIS微波加热过程分段温度预测模型
王伟,周新志
(1.四川大学 电子信息学院,四川 成都 610065; 2.四川大学 智能控制研究所, 四川 成都 610064)
ANFIS微波加热过程分段温度预测模型
王伟1, 2,周新志1, 2
(1.四川大学 电子信息学院,四川 成都 610065; 2.四川大学 智能控制研究所, 四川 成都 610064)
摘要:在微波加热过程中加热介质在不同温度阶段有不同的内部特性,传统的温度预测方法难于同时对加热介质低温段与高温段温度取得满意的预测结果。为此提出了一种基于ANFIS 的分段温度预测模型,该方法建立基于K均值聚类法的温度划分机制,并采用不同结构的ANFIS预测加热介质不同温度阶段的温度。低温阶段构建常规ANFIS预测温度,高温阶段利用减法聚类能从数据中确定模糊规则的特性构建ANFIS预测温度。仿真结果表明,与采用单一结构的ANFIS和BP(back propagation)神经网络的预测结果相比,ANFIS分段温度预测模型可同时在加热介质低温段与高温段取得较好的预测结果,模型效率可达到97.41%,显著提高了预测准确率,这有助于提高实际微波加热过程的生产效率和安全性。
关键词:微波加热过程;分段温度预测;K均值聚类;ANFIS;BP神经网络;减法聚类
中文引用格式:王伟,周新志. ANFIS微波加热过程分段温度预测模型[J]. 智能系统学报, 2016, 11(1): 61-69.
英文引用格式:WANG Wei, ZHOU Xinzhi. Temperature-sectioned prediction model for microwave heating process based on adaptive network-based fuzzy inference system[J]. CAAI Transactions on Intelligent Systems, 2016, 11(1): 61-69.
作为一种新型加热方式,微波加热以其高效、清洁、环保的特点,广泛应用于化工、食品、冶金、材料等领域[1-3],并逐渐成为实现我国节能减排目标的绿色工艺手段之一。在微波加热过程中,加热介质内部特性诸如介电常数、电导率、热传导系数等随温度升高而变化,使得温度变化复杂,在加热过程中会出现热失控现象[1],对生产造成危险。因此对加热介质温度的准确预测是保证大功率微波源加热过程安全性、可靠性,使其用于实际加热过程的重要研究课题之一。
目前,国内外学者针对温度预测方法已做了大量研究。Pedreno-Molina等提出RBF神经网络与多项式矩阵方程相结合的思想用于微波辅助干燥过程温度的预测[4]。TRIPATHY P. P. 等于2009年使用神经网络方法预测日光干燥过程的食品温度,取得了满意的结果[5]。国内学者王安娜等于2006年利用粒子群算法优化BP网络,建立新的钢水终点温度预报模型,提高了LF炉钢水温度的预测速度和精度[6]。2012年崔桂梅等利用数据挖掘理论提取样本数据特征,建立了T-S模糊神经网络模型预测高炉铁水的温度,预测结果验证了其方法优于BP网络预测[7]。然而,上述方法也有不足之处。其一是神经网络的温度预测方法对样本要求较高,并且无法充分利用已有的经验知识。其二是以上方法均未考虑加热介质不同温度阶段内部特性的不同对其温度的影响。
针对已有研究成果的不足,本文首次提出采用自适应神经模糊推理系统来预测微波加热过程加热介质的温度。ANFIS[8]将神经网络与模糊系统结合,结合模糊系统可以利用专家知识、对样本要求低的特点弥补神经网络的不足,特别适合于复杂过程的预测问题。在此基础上,根据加热介质在不同温度阶段有不同的内部特性,引入K均值聚类法将加热介质温度分为低温阶段和高温阶段分别进行预测。以下将从数据预处理、构建低温、高温阶段温度预测模型以及仿真结果等方面阐述该预测模型及其结果。
1数据预处理
在微波加热过程中,传感器测量的实际温度信号经常会掺杂噪声,呈现出温度突变等非平稳特性,这样的温度突变点不能仅仅将其当做噪声去除掉,而需要考虑微波加热过程中出现的热失控现象[1]。区别于传统傅里叶变换去噪方法,小波变换在非平稳信号的去噪方面具有突出的优越性。研究表明,Donoho提出的小波阈值去噪方法是工程中应用最广泛的方法[9]。在此使用小波阈值去噪方法对传感器测量的含噪温度信号进行处理。含噪温度数据可按式(1)定义为

(1)
式中:s(t)为原始温度数据,n(t)是服从正态分布、不相关且方差为常量的高斯白噪声。
小波阈值去噪方法首先选取合适的小波基对含噪温度信号进行小波分解,然后根据选择的阈值函数和阈值对分解后的高频系数进行阈值量化处理,最后根据低频小波系数和去噪后的高频小波系数重构信号,获得去噪温度信号[10]。
从上述小波去噪过程可知,信号去噪效果的好坏与小波基的选择、分解的层数、阈值函数的选取以及阈值的确定有直接关系。阈值函数分为软、硬两种,相比于硬阈值函数软阈值函数去噪效果更加平滑,因此本文选择软阈值函数,软阈值函数定义如式(2)所示:
(2)
阈值由极大极小阈值估计方法确定,产生一个最小均方误差的极值作为阈值。除了确定阈值函数和阈值的估计方法,还需要选择合适的小波基和最佳分解层数。在此采用实验的方法确定小波基以及分解层数,并采用信噪比(SNR)、均方根误差(RMSE)以及平滑度指标[11]作为去噪效果的评价标准。在综合测试了几种常用的小波基以及不同的分解层数后,得出如表1所示的结果。
表1不同小波基以及分解层数去噪效果的评价结果
Table1De-noising result evaluation of different wavelet basis and destruct levels
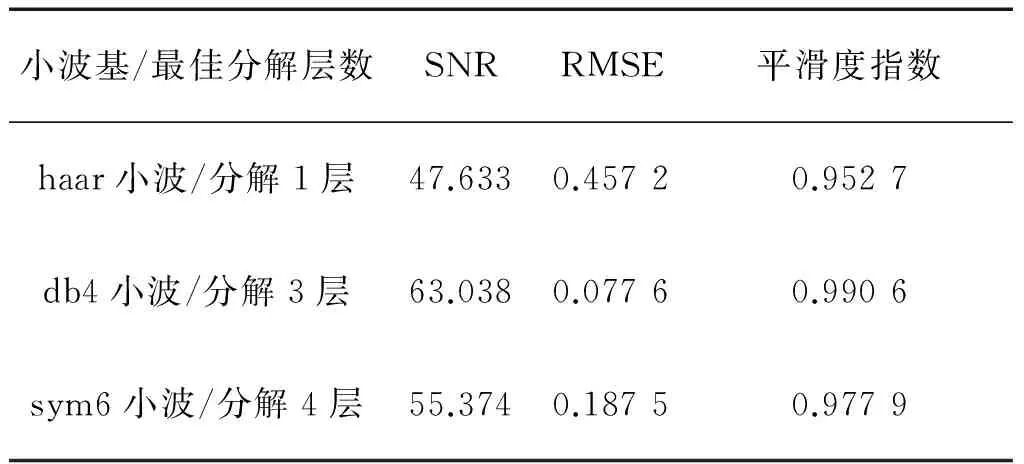
小波基/最佳分解层数SNRRMSE平滑度指数haar小波/分解1层47.6330.45720.9527db4小波/分解3层63.0380.07760.9906sym6小波/分解4层55.3740.18750.9779
从表1的去噪效果可以看到,选用db4小波对原始温度数据进行3层分解,信噪比可以达到63.038,高于使用db4小波和sym6小波去噪信号的信噪比;均方根误差为0.077 6,比db4小波和sym6小波的均方根误差更小;平滑度指数略高于db4小波和sym6小波,表示去噪信号更加平滑。因此选用db4小波对原始温度数据进行3层分解,可以达到很好的去噪效果,其原始含噪温度数据与去噪之后的温度数据如图1所示。
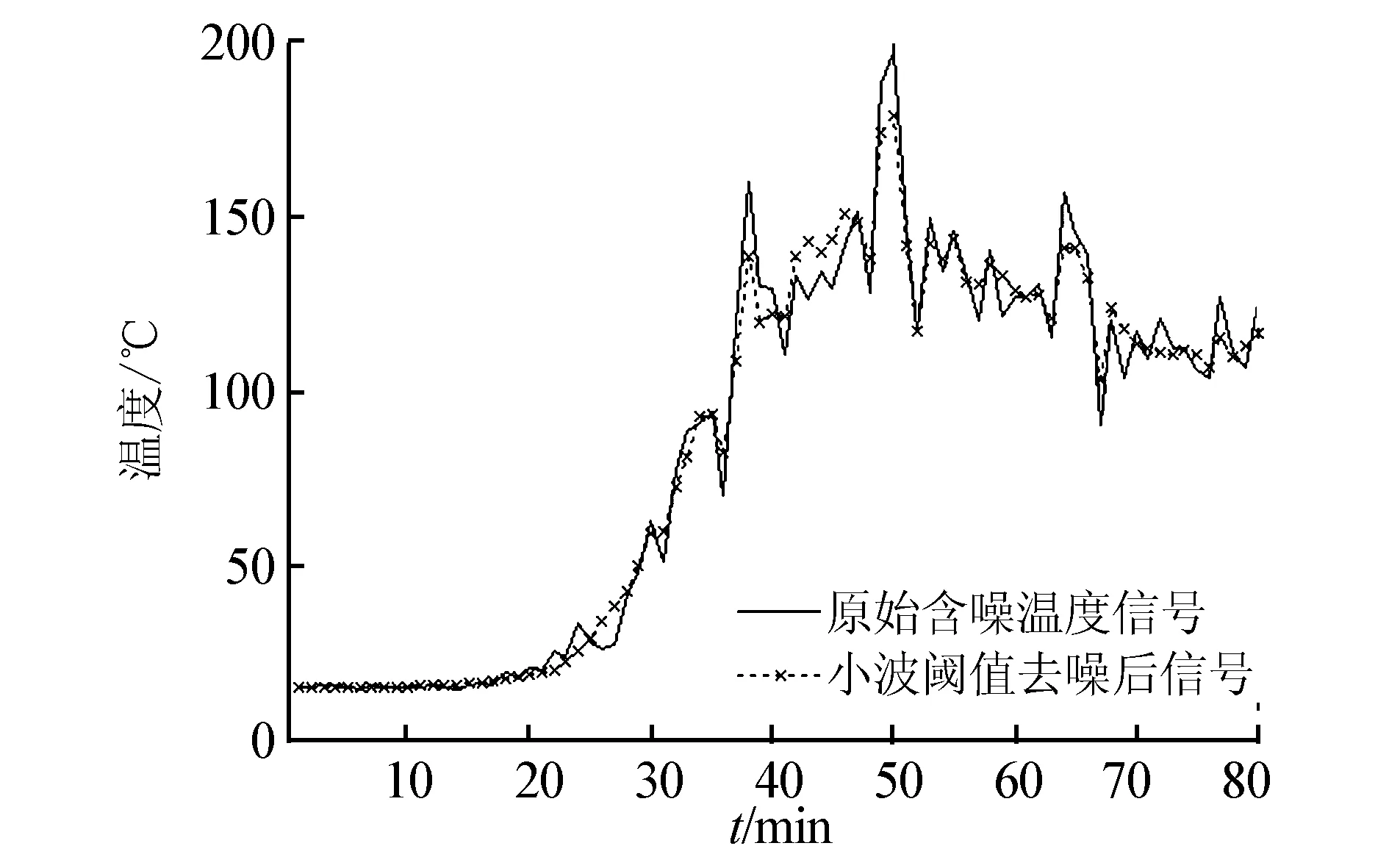
图1 阈值去噪效果Fig.1 Wavelet threshold method de-noising results
从图1可以看到,使用db4小波基进行3层分解去噪可以很好地滤除随机噪声,信号重构精度较高,而且较好地保留了原始温度数据的细节信息。
2ANFIS分段温度预测模型
从图1可以看出微波加热过程介质温度的变化大致分为以下3个阶段:低温阶段、升温阶段、高温阶段。在低温阶段,加热介质的温度变化较为平稳,加热介质内部特征变化不大,其温度较容易预测;而在高温阶段,加热介质内部特性随温度发生变化,反映为温度呈现波动性变化,温度预测较低温阶段困难。根据这一现象,建立了基于K均值聚类法的温度划分机制,将加热介质温度数据划分为低温阶段和高温阶段,采用不同结构的ANFIS分别进行预测。

图2 温度划分机制Fig.2 Temperature sectioned mechanism
2.1K均值聚类法温度划分机制
对于温度数据的划分,K均值聚类方法可以方便地将数据按其特征进行分类,同一个聚合类中数据的特征比不同聚合类中数据的特征更为相近。故利用K均值聚类算法将加热介质温度数据划分为低温区数据和高温区数据。算法首先从样本数据中选择2个数据点作为初始低温区与高温区的聚类中心,然后计算每个样本数据点到初始聚类中心的欧氏距离:
式中:Di,j表示第i个样本数据和第j个样本数据之间的距离,i、j=1,2,…,n,n为样本数据维数;xik与xjk分别表示第i个数据点与第j个数据点的第k维分量。按欧氏距离将每个数据点分到最近的初始聚类中心,之后重新计算这2个聚类的中心,直到2个聚类中心不再发生变化,即划分了低温区域数据与高温区域数据。流程图如图2所示。
2.2ANFIS分段温度预测模型


(a)训练阶段
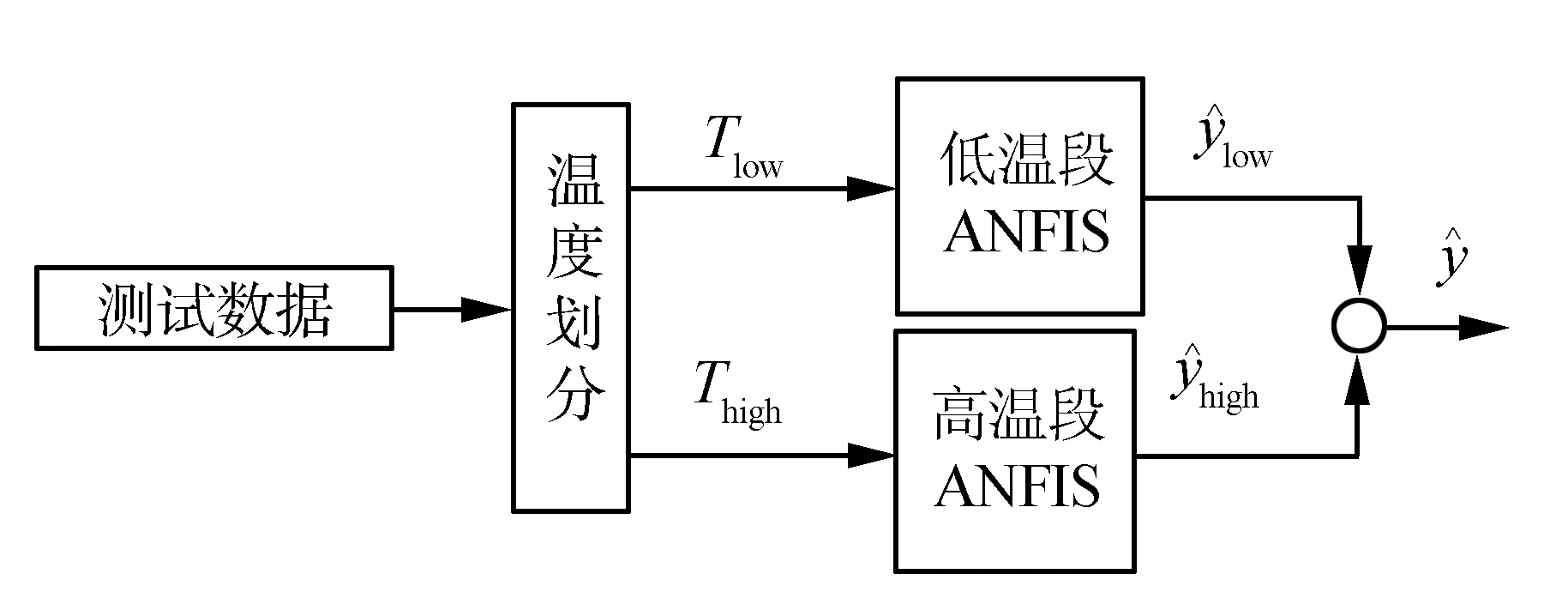
(b)预测阶段图3 ANFIS分段温度预测模型Fig. 3 ANFIS temperature sectioned prediction model
2.3构建低温段ANFIS
低温段构建了基于零阶Sugeno模糊模型的ANFIS[12-15],即系统输出为系统输入量的线性组合,采用5层网络结构[16-19],系统结构如图4所示。
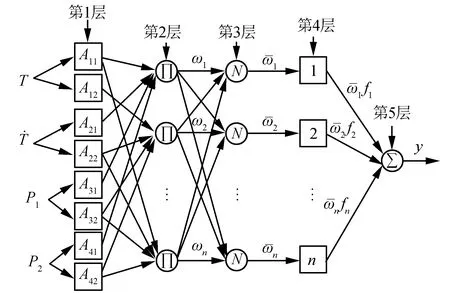
图4 ANFIS结构Fig. 4 The structure of ANFIS
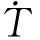
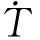
第1层为模糊化层,计算各输入变量所对应模糊集合的隶属度函数值,该层每个节点均为一个自适应节点,节点输出按式(3)计算:
(3)
式中:μAik表示计算第i个输入变量属于第k个模糊语言变量的隶属度函数值。
第2层为模糊规则层,用来匹配模糊规则的前件,对输入量进行模糊与运算,计算出每条规则的适应度:
(4)
第3层为归一化层,对第2层的输出进行归一化计算,第i个节点计算第i条规则的权重与所有规则的权重之和的比值:
(5)
第4层为去模糊化层,计算每条规则的输出:
(6)
该层每个节点为自适应节点,{pi,qi,ri,si,ti}称为后件参数。
第5层为输出层,对第4层的输出进行求和得到系统输出:
(7)
从上述推理过程可知,ANFIS网络输出可表示为后件参数{pi,qi,ri,si,ti}的线性组合:
(8)
后件参数{pi,qi,ri,si,ti}按如下方法进行调整。定义误差代价函数[20]为
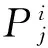
(9)
式中β为学习率。
由于低温阶段的介质温度比较平稳,输入量变化较小,因此低温段预测构建的ANFIS前件将每个输入变量分为两级语言变量,即大(large)和小(small)。模糊隶属度函数常选择钟形隶属度函数或者高斯隶属度函数,但对于隶属度函数的选择一般依据经验设定,尚无确定的理论依据。在此,我们对比了钟形隶属度函数和高斯隶属度函数在加热介质低温段的预测效果,如图5所示。

(a)实际低温区温度

(b)高斯隶属函数预测

(c)钟形隶属函数预测图5 钟形隶属函数与高斯隶属函数低温段温度预测结果Fig.5 Prediction result in low temperature use bell membership function and gauss membership function
图5(a)为实际的低温温度曲线,图5(b)和图5(c)分别为使用高斯隶属函数和钟形隶属函数的预测结果,可以观察到这2种隶属函数在低温阶段都有着较好的预测效果。再以均方根误差(RMSE)、平均误差(ME)和标准差(STD)作为评价标准,得到2种隶属函数的预测结果评价,如表2所示。
表2钟形隶属函数与高斯隶属函数低温段温度预测结果对比
Table2Prediction results in low temperature between bell membership function and gauss membership function

隶属函数RMSESTDME钟形隶属函数2.1222.5601.472高斯隶属函数2.2052.6591.533
从表2的结果可以看出,选取钟形隶属度函数的ANFIS在低温段的温度预测结果均方根误差为2.122,平均误差为1.472,要略好于选取高斯隶属度函数的ANFIS。因此,我们确定模糊集合的隶属度函数为钟形函数的形式,函数表达式如式(10):
(10)
在确定了隶属度函数之后,需要确定钟形隶属度函数的具体参数{a,b,c}。ANFIS系统利用BP反向传播算法和最小二乘算法[21]来计算隶属度函数的最佳参数[11]。首先固定前件参数,采用梯度下降法调节后件参数;此后,将误差信号沿网络反向传播,在反向过程中,固定后件参数,调节前件参数。为避免梯度下降法容易陷入局部极小值的缺点,采用附加动量因子[22]的方法来寻找ANFIS的前件参数最优解,这样可以综合考虑目标误差函数在梯度上的作用和在误差曲面上变化趋势所带来的影响,具体参数调整公式如式(11)~(13):
(11)
(12)
(13)
式中:i=1,2,3,4为输入变量维数,j=1,2为输入变量的语言变量级数,k为迭代次数,β(k)为第k步学习率,λ为动量因子,取值范围为(0,1),设f为系统输出,yd为期望输出,则E(k)=(yd-f)2/2。
调整之后的低温段ANFIS输入对应的模糊集合及隶属度函数参数a、b、c的值如表3所示。
表3低温段ANFIS输入量对应的模糊集合及隶属函数参数调整值
Table 3The fuzzy sets and membership function parameters of each input in low temperature ANFIS

输入量模糊集合模糊语言值abc TA11SMALL81.72.015.2TA12LARGE81.72.2178.TA21SMALL52.11.9-39.TA22LARGE42.11.944.6P1A31SMALL21.22.3-0.8P1A32LARGE21.62.043.1P2A41SMALL21.62.6-0.1P2A42LARGE21.82.143.5
2.3构建高温段ANFIS
由于加热介质内部特性随温度升高而发生变化,其高温段的温度变化更复杂,对低温段适用的ANFIS模型不再适合于高温段温度预测,因此需要构建高温段ANFIS预测加热介质的温度。考虑到减法聚类[14-15, 23-25]算法无需预先设定聚类数,可以根据样本数据的特征自行确定聚类数目以及聚类中心的优点[13],在高温段的ANFIS预测模型中,使用了减法聚类算法确定高温段的输入和输出语言变量的隶属度函数个数和模糊规则个数,使得到的ANFIS结构更加符合输入数据的特征。减法聚类过程如下:
(14)

2)按式(15)修改每一个数据点的聚类中心潜在值:
(15)
式中:pi′表示更新之后的潜在值,γb定义了一个聚类中心潜在值显著减小的邻域半径,朱广宇等[26]给出了式(16)用来确定γa、γb:
(16)
影响减法聚类结果的最主要参数为γa,我们将其称为接受域,通常取值范围为[0,1]。在构建高温段ANFIS的预测模型时,通过实验的方式来确定减法聚类算法的接受域,变量γa以步长0.1从0.3变化至0.8,我们按式(17)计算预测模型效率系数,并得到如图6所示结果。
(17)
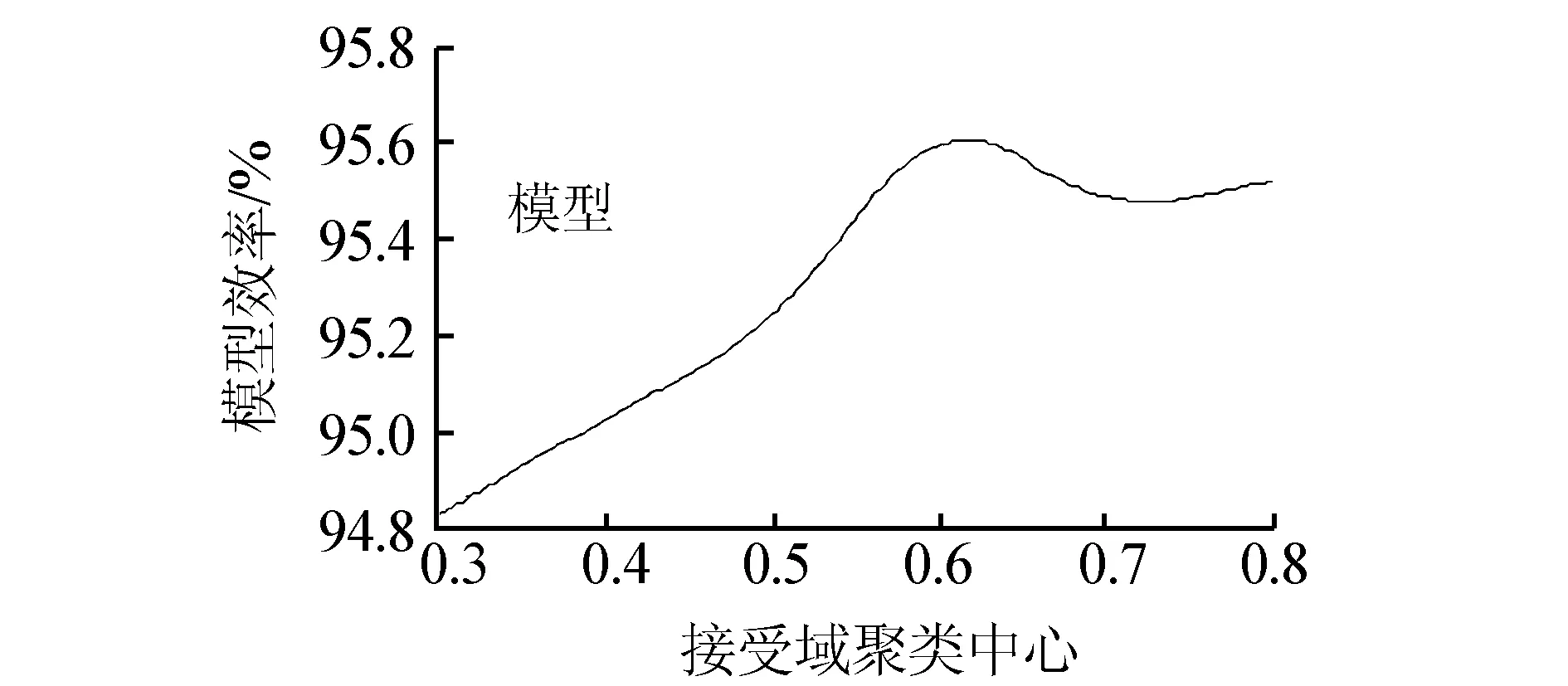
图6 伴随聚类中心接受域变化的模型效率曲线Fig.6 Model efficiency curve with the change of clustering center accept ratio
图6描述了伴随聚类中心接受域γa变化的减法聚类ANFIS的模型效率。从中可以明显观察到模型的性能在接受域为0.6时最高,为95.57%,因此聚类中心的接受域γa设定为0.6。这样在高温段构造的自适应神经模糊推理系统中共产生了4条规则。
3仿真结果及分析
为了验证本文提出的微波加热过程温度分段预测方法的性能,使用由南京三乐公司大功率微波煤炭干燥生产线上实际采集的过程数据进行仿真。该大功率微波煤炭干燥生产线共包含5个微波加热腔体,每个微波加热腔体包含2个微波功率源,在此采集了1号和2号微波腔体共233组数据。我们选择1号微波加热腔体的151组数据作为训练数据;选择2号微波加热腔体的82组数据作为预测数据,利用MATLAB进行仿真验证,并与BP神经网络、单一的ANFIS温度预测结果进行对比。分段温度预测方法在低温段使用的ANFIS指定隶属度函数为钟形,每个输入对应两级语言变量,共有16条模糊规则,训练300次;高温段ANFIS使用减法聚类算法,γa取0.6,训练300次,确定了4条模糊规则。根据经验公式,BP神经网络隐层节点数为12,学习率为0.1,共训练300次。单一的ANFIS温度预测指定隶属度函数为钟形,每个输入对应两级语言变量,共有16条模糊规则,训练300次。分别使用以上3种预测方法得到了如图7(b)~(d)所示的预测结果,图7(a)为实际预测数据样本。
(a)实际预测数据样本
(b)BP网络预测结果

(c)单一ANFIS预测结果

(d)ANFIS分段温度预测结果图7 3种预测方法的预测结果与实际预测数据样本的比较Fig.7 Comparison of results between Original prediction samples and three different prediction methods
由图7可以看出,BP网络在高温段的预测效果不理想,很难预测出加热介质温度的波动以及出现的峰值;单一的ANFIS预测结果要好于BP网络,低温段与高温段都有着较好的预测准确率,但是在峰值部分容易出现预测结果过高;相比起前2种预测方法,本文使用的ANFIS温度分段预测方法在低温段与高温段的预测结果更优,低温段预测结果与实际数据拟合较好,高温段在峰值部分没有出现预测结果过高的现象,总体趋势与实际数据接近。3种模型下加热介质部分温度预测值与实际值比较见表4。
表43种模型下加热介质部分温度预测值与实际值比较
Table 4Comparison of results between prediction value and real value with three different models

样本号温度/℃实际值ANFIS温度分段单一ANFISBP网络117.018.018.118.9225.721.520.819.0365.956.455.479.4495.9105.1111.5106.45107.0107.2103.396.16111.9114.8117.6106.77117.9112.3112.3109.98121.8119.1118.4110.59125.9129.9132.9121.910131.0125.5126.5121.911140.1138.7143.5128.912144.9150.0150.5129.913156.9142.7126.2129.614178.1174.3186.4170.615204.7199.0191.3160.5
3种模型预测性能对比见表5。选用以下指标作为模型评价标准:均方根误差(RMSE)、标准差(STD)、模型效率(R2)、误差项平方和(SSE)和平均绝对误差(MAE)。ANFIS温度分段预测方法的均方根误差为8.08,标准差9.64,误差项平方和5 354.9,平均绝对误差5.12。几项评价指标均低于单一ANFIS预测方式和BP网络预测,模型效率系数达到97.41%,高于其他预测方法。这表明提出的预测模型结果精度更高、性能更优、适应性更强。这是因为加热介质在不同温度下的内部特性不同,采取将温度分段,在低温段与高温段采用不同结构的ANFIS,根据其数据反映的加热介质在该温度段的内部特性确定模糊规则数与隶属度函数参数,更加适合于微波加热过程的温度预测。
表53种预测方法性能
Table 5The performance of three different prediction methods

预测方法RMSESTDSSEMAER2/%ANFIS温度分段8.089.645354.95.1297.41单一ANFIS9.3311.037145.55.9996.54BP网络10.9710.199875.67.3195.21
4结束语
在微波加热的过程中,加热介质在不同温度阶段有不同的内部特性,其温度在低温阶段与高温阶段有不同的变化趋势。基于此,本文提出了一种基于ANFIS的分段温度预测方法,将加热介质温度划分为低温阶段和高温阶段分别进行预测。在低温段使用常规ANFIS进行预测,在高温阶段使用减法聚类从样本中提取模糊规则,构建ANFIS进行预测。预测结果表明,基于ANFIS的温度分段预测方法在样本数量有限的情况下取得了令人满意的准确率,在低温段与高温段都有着良好的表现,优于传统的BP网络与单一ANFIS的预测结果。对于提高微波加热过程的效率和安全性具有重要的参考价值。
参考文献:
[1]刘长军, 申东雨. 微波加热陶瓷中热失控现象的分析与控制[J]. 中国科学 E辑: 技术科学, 2008, 38(7): 1097-1105.
LIU Changjun, SHEN Dongyu. Analysis and control of the thermal runaway of ceramic slab underheating ceramics[J]. Science in China series e: technological science, 2008, 51(12): 2233-2241.

[3]WEI W, YIN H M, TANG J M. An optimal control problem for microwave heating[J]. Nonlinear analysis: theory, methods & applications, 2012, 75(4): 2024-2036.
[5]TRIPATHY P P, KUMAR S. Neural network approach for food temperature prediction during solar drying[J]. International journal of thermal sciences, 2009, 48(7): 1452-1459.
[6]王安娜, 陶子玉, 姜茂发, 等. 基于PSO和BP网络的LF炉钢水温度智能预测[J]. 控制与决策, 2006, 21(7): 814-816, 820.
WANG Anna, TAO Ziyu, JIANG Maofa, et al. Intelligence temperature prediction of molten steel in LF based on PSO combined with BP neural network[J]. Control and decision, 2006, 21(7): 814-816, 820.
[7]崔桂梅, 李静, 张勇, 等. 基于T-S模糊神经网络模型的高炉铁水温度预测建模[J]. 钢铁, 2013, 48(11): 11-15.
CUI Guimei, LI Jing, ZHANG Yong, et al. Prediction modeling study for blast furnace hot metal temperature based on T-S fuzzy neural network model[J]. Iron and steel, 2013, 48(11): 11-15.
[8]DONOHO D L. De-noising by soft-thresholding[J]. IEEE transactions on information theory, 1995, 41(3): 613-627.
[9]陶珂, 朱建军. 小波去噪质量评价方法的对比研究[J]. 大地测量与地球动力学, 2012, 32(2): 128-133.
TAO Ke, ZHU Jianjun. A comparative study on validity assessment of wavelet De-noising[J]. Journal of geodesy and geodynamics, 2012, 32(2): 128-133.
[10]茹斌, 张天伟, 王宇欣. 基于小波去噪及ARMA模型的故障率预测方法研究[J]. 测控技术, 2014, 33(10): 43-46, 50.
RU Bin, ZHANG Tianwei, WANG Yuxin. Research on the method of failure rate prediction based on wavelet and ARMA model[J]. Measurement & control technology, 2014, 33(10): 43-46, 50.
[11]JANG J S R. ANFIS: Adaptive-network-based fuzzy inference system[J]. IEEE transactions on systems, man and cybernetics, 1993, 23(3): 665-685.
[12]TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transactions on systems, man and cybernetics, 1995, SMC-15(1): 116-132.
[13]NAYAK P C, SUDHEER K P. Fuzzy model identification based on cluster estimation for reservoir inflow forecasting[J]. Hydrological processes, 2008, 22(6): 827-841.
[14]MIRRASHID M. Earthquake magnitude prediction by adaptive neuro-fuzzy inference system (ANFIS) based on fuzzy C-means algorithm[J]. Nature hazards, 2014, 74(3): 1577-1593.
[15]Al-MAYYAHI A, WANG W, BIRCH P. Adaptive neuro-fuzzy technique for autonomous ground vehicle navigation[J]. Robotics, 2014, 3(4): 349-370.
[16]HIDAYAT, PRAMONOHADI S, SARJIYA, et al. A comparative study of PID, ANFIS and hybrid PID-ANFIS controllers for speed control of Brushless DC Motor drive[C]//Proceedings of International Conference on Computer, Control, Informatics and Its Applications (IC3INA). Jakarta, Indonesia, 2013: 117-122.
[17]蒋浩宇, 富立, 范耀祖. ANFIS在车辆导航系统信息融合中应用的仿真研究[J]. 系统仿真学报, 2006, 18(4): 1051-1054.
JIANG Haoyu, FU Li, FAN Yaozu. Simulation study on application of ANFIS for information fusion of vehicle navigation system[J]. Journal of system simulation, 2006, 18(4): 1051-1054.
[18]夏琳琳, 苗贵娟, 初妍, 等. 基于自适应神经模糊系统的足球机器人射门点的确定[J]. 智能系统学报, 2013, 8(2): 143-148.
XIA Linlin, MIAO Guijuan, CHU Yan, et al. Determination of shooting point for soccer robot based upon adaptive neuro-fuzzy in ference system[J]. CAAI transactions on intelligent systems, 2013, 8(2): 143-148.
[19]张秀玲, 逄宗鹏, 李少清, 等. ANFIS的板形控制动态影响矩阵方法[J]. 智能系统学报, 2010, 5(4): 360-365.
ZHANG Xiuling, PANG Zongpeng, LI Shaoqing, et al. A dynamic influence matrix method for flatness control based on adaptive-network-based fuzzy inference systems[J]. CAAI transactions on intelligent systems, 2010, 5(4): 360-365.
[20]YU Xiaohu, CHEN guoan. Efficient backpropagation learning using optimal learning rate and momentum[J]. Neural networks, 1997, 10(3): 517-527.
[21]蒋静芝, 孟相如, 李欢, 等. 减法聚类-ANFIS在网络故障诊断的应用研究[J]. 计算机工程与应用, 2011, 47(8): 76-78, 86.
JIANG Jingzhi, MENG Xiangru, LI Huan, et al. Study on application of subtractive clustering and adaptive network-based fuzzy inference system in network fault diagnosis[J]. Computer engineering and applications, 2011, 47(8): 76-78, 86.
[22]PLATON R, AMAZOUZ M. Modeling of a drying process using subtractive clustering based system identification[C]//Proceedings of the Joint 9thIFSA World Congress and 20thNAFIPS International Conference. Vancouver, BC, Canada, 2001: 2994-2999.
[23]王增福, 潘泉, 郎林, 等. 基于减法聚类的动态航迹聚类算法[J]. 系统仿真学报, 2009, 21(16): 5240-5243, 5246.
WANG Zengfu, PAN Quan, LANG Lin, et al. Dynamic track cluster algorithm based on subtractive clustering[J]. Journal of system simulation, 2009, 21(6): 5240-5243, 5246.
[24]朱广宇, 刘克, 乔梁. 基于T-S模型的交通状态自适应神经模糊推理系统建模与仿真[J]. 北京交通大学学报, 2012, 36(6): 96-101.
ZHU Guangyu, LIU Ke, QIAO Liang. Modeling and simulation for traffic states with ANFIS based on T-S model[J]. Journal of Beijing jiaotong University, 2012, 36(6): 96-101.
[25]张智星, 孙春在, [日]水谷英二. 神经-模糊和软计算[M]. 西安: 西安交通大学出版社, 2000: 346-401.
ZHANG Zhixing, SUN Chunzai, MIZUTANI E. Neuro-fuzzy and soft computing[M]. Xi’an: Prentice Hall, 2000: 346-401.
[26]李国勇, 杨丽娟. 神经·模糊·预测控制及其MATLAB实现[M]. 3版. 北京: 电子工业出版社, 2013: 305-379.
LI Guoyong, YANG Lijuan. Neural-fuzzy-predictive control and the realization by MATLAB[M]. 3rded. Beijing: Publishing House of Electronics Industry, 2013: 305-379.
Temperature-sectioned prediction model for microwave heating process based on adaptive network-based fuzzy inference system
WANG Wei1,2, ZHOU Xinzhi1,2
(1. College of Electronic Information, Sichuan University, Chengdu 610065, China; 2. Institute of Intelligent Control, Sichuan University, Chengdu 610064, China)
Abstract:During the microwave heating process, materials in different temperature regions have different internal characteristics. Using traditional temperature forecasting methods, it is difficult to obtain satisfactory prediction results for both low-and high-temperature sections in a medium. To solve this problem, this study proposes a new temperature-sectioned forecasting model based on the ANFIS (adaptive neuro-fuzzy inference system). For this method, we established a temperature-division mechanism based on K-means clustering. Additionally, we used an ANFIS with different structures to forecast the temperature of the heated medium at different stages. We also constructed a conventional ANFIS to predict a material’s low temperature and a subtraction-clustering ANFIS that determines the fuzzy rules from data to predict a material’s high temperature. Simulation results demonstrate that the proposed method achieves satisfactory results for both low- and high-temperature sections when compared to ANFISs and BP(back propagation) networks with a single structure. Model efficiency can reach 97.41% and the prediction accuracy is significantly improved. The proposed model can improve the efficiency and safety of the microwave heating process.
Keywords:microwave heating process; sectioned temperature prediction; K-means clustering; adaptive Neuro-Fuzzy inference system; BP nerve network; subtraction clustering
DOI:10.11992/tis.201501028
收稿日期:2015-01-30. 网络出版日期:2015-12-29.
基金项目:国家“973”计划资助项目(2013CB328903).
通信作者:周新志.E-mail: xz.zhou@scu.edu.cn.
中图分类号:TP18; TP301.6
文献标志码:A
文章编号:1673-4785(2016)01-0061-09
作者简介:

王伟,男,1989年生,硕士研究生,主要研究方向为智能控制。

周新志,男,1966年生,教授,博士,主要研究方向为人工智能、智能控制技术及应用。作为主要研究者或项目负责人承担了国家“973”计划、国家自然科学基金项目、四川省科技攻关项目等多项,获国家专利2项,发表学术论文30余篇。
网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20151229.0844.022.html

