宽带噪声调频信号对脉冲压缩的干扰机理研究

孙清清,郑　坤,曹旭源,王　洪

(1.电子信息控制重点实验室,成都 610036;2.电子科技大学 电子工程学院,成都 611731)

宽带噪声调频信号对脉冲压缩的干扰机理研究

孙清清1,2,郑坤1,曹旭源1,王洪2

(1.电子信息控制重点实验室,成都 610036;2.电子科技大学 电子工程学院,成都 611731)

摘要：为了分析宽带噪声调频信号对脉冲压缩滤波器的干扰效应,引入随机微分的理论,建立了调频噪声干扰信号所满足的福克-普朗克(Fokker-Planck)方程,求解得出干扰信号通过脉压滤波器输出时域包络的概率密度分布函数。基于干扰信号输出的分布函数,采用“等效视数”和幅度压制系数作为干扰效果评估指标,仿真分析了噪声调频干扰信号的带宽、幅度以及频率引导误差对干扰效果的影响。

关键词:干扰机理;脉冲压缩;噪声调频干扰;随机微分

0引言

有源压制式噪声干扰是脉冲压缩雷达常见的干扰形式之一。为了具体评估压制式噪声的干扰效应,需要深入雷达信号处理的各个主要环节,得到干扰参数对雷达信号处理相关环节的具体影响量值。这对干扰机设计过程中的干扰参数选择具有重要的参考价值。脉冲压缩匹配滤波器是雷达信号处理的一个重要环节。评估压制干扰对其产生的具体效果在雷达设计和试验中仍具有十分重要的意义。

目前,已有不少针对压制式干扰对脉冲压缩滤波器的干扰效果评估的研究成果,大部分研究是基于统计模型仿真的方法评估干扰的效果[1-2],仿真的方法难以对于干扰参数的具体影响量值进行一般性的评估。也有研究针对具体的干扰参数,如文献[3-4]基于统计学理论,研究了宽带调频噪声干扰对线性调频匹配滤波器的干扰效果,推导出最大输出包络起伏的指标下最优的调制噪声带宽以及噪声调频干扰带宽与瞬时调频斜率之间的关系。这对于干扰使用的调制噪声特性研究具有参考价值,但实际中调制噪声带宽指标要求一般不是很严格。理想的评估方法是得到干扰通过滤波器后的概率密度分布函数,利用概率密度函数的丰富性态可分析各类干扰参数的具体影响机理。如文献[5-6]采用基于随机微分方法推导出了理想调频噪声干扰信号通过线性调频脉压滤波器的输出信号概率密度分布函数的含时解,并基于信息准则对射频噪声的干扰效果进行评估。在实际实施压制干扰中,理想调频噪声干扰是不可能实现的。调制噪声带宽无穷大的情况下干扰信号功率谱趋于一个尖峰,即干扰带宽很小,属于窄带调频噪声干扰信号,实际中通常使用宽带噪声调频干扰实施瞄准-阻塞式干扰。本文针对常规的宽带噪声调频干扰对脉压滤波器的干扰效果,得到干扰经过匹配滤波器后输出包络的概率密度函数,分别研究不同干扰参数的影响机理。

本文针对常用于瞄准-阻塞式干扰的宽带噪声调频信号,首先对噪声调频干扰信号的统计特性进行了分析,然后推导出噪声调频干扰通过脉压滤波器后时域包络的概率密度函数,并基于得到概率密度函数提出输出信干比和幅度压制系数两种干扰评估指标,最后分别研究噪声干扰信号带宽、干扰信号幅度和频率引导误差对干扰效果的影响。

1宽带调频噪声干扰信号统计特性分析

理想噪声调频干扰信号为广义平稳随机过程,可表示为[7]

(1)

(2)

则随机过程e(t)的功率谱密度可表示为

(3)

推导可得高斯过程e(t+τ)-e(t)的方差函数:

(4)

噪声调频信号的功率谱:

(5)

其中,△Ωn=2πBn,mfe=KFMσn/Bn=fde/Bn为有效调频指数,fde为有效调频带宽,当mfe≫1时噪声调频干扰信号表现为宽带调频。

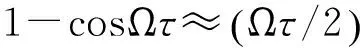
(6)

(7)

2基于随机微分的宽带调频噪声信号分析

本节通过推导得到宽带噪声调频干扰通过脉压滤波器后的概率密度函数。首先建立噪声调频干扰信号所满足的福克-普朗克方程,利用群移傅里叶变换将偏微分方程转换为时变系数的线性齐次常微分方程组,然后使用龙格库塔(Runge-Kutta)数值积分法求解方程组,最后通过群移逆傅里叶变换得到概率密度函数的含时解。

假设雷达接收机中频滤波器输入的噪声调频干扰信号为

(8)

线性调频脉压滤波器的传递函数为

(9)

则滤波器的输出信号:

(10)

(11)

当t≤τ≤t+△t时,

因此

(12)

式(11)中,

(13)

将式(13)代入式(11)得到

(14)

因此

(15)

因为

则

(16)

令z(t)=r(t)ejθ(t),将式(16)转化为极坐标的形式:

(17)

式(17)左端:

(18)

式(17)右端:

(19)

联立式(17)、(18)、(19)可得式(20):

(20)

其中

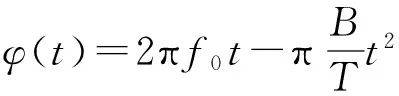
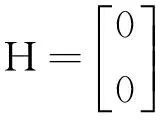
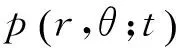
(21)

利用群移傅里叶变换(MGFT)的微分算子[9],可以将式(21)写成:

(22)

对式(22)进行MGFT变换可以得到

(23)

则式(23)可化简为

(24)

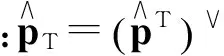
根据矩阵Kronecker积的性质,M=I⊗A+BT⊗I,即

其中,B为对角矩阵,且b0,0=0,则式(24)可化简为时变系数的线性常微分方程组:

(25)

(26)

(27)

由此,得到干扰通过线性调频匹配滤波器输出的幅度分布,如式(27),后面将基于此分布函数讨论干扰效应的评估指标。

3干扰效应评估指标

调频噪声干扰信号通过匹配滤波器后输出仍是随机过程。依据最佳干扰波形理论输出信号的信息熵越大即时域波形的起伏越大干扰效果越好,物理意义上表示为输出信号“交流”分量功率占总功率的比重越大。基于最佳波形准则,信息熵、输出信噪比[5,10]和“等效视数”[3]等都可用于评估干扰的效果。本文定义干扰效果的评估指标“等效视数”(ENL)为

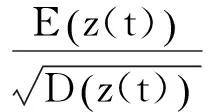
(28)

“等效视数”的倒数反映了信号时域波形的起伏大小。“等效视数”的数值越大信号波形起伏越小干扰效果越差,反之干扰效果越好。

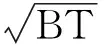
(29)

由此,本文定义另一个干扰评估指标幅度压制系数,以pfa=C时在接收机输入端干扰幅度与信号幅度的比值定义为幅度压制系数KA,C为常数,即

(30)

幅度压制系数与一般的功率压制系数本质含义是类似的,对于脉压滤波器后的恒虚警检测等信号处理过程都是基于信号幅度的检测。因此,幅度压制系数理论上更符合干扰效果评估的需求。

4仿真实例

线性调频脉压滤波器是脉冲压缩的一种常用方法。本文主要研究宽带噪声调频干扰信号通过线性调频脉压滤波器输出的干扰效果,线性调频脉压滤波器的时域表达形式为

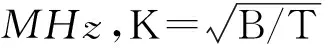
如式(8),当干扰信号幅度Uj=1,干扰信号载频fj=75MHz,即干扰频率引导误差δf=|f0-fj|=0,式(27)中的t=10μs,干扰通过脉压滤波器后输出的概率密度函数曲线如图1。图中横坐标表示幅度值,纵坐标为概率密度函数值,概率密度函数曲线类似于正态分布曲线,输出幅度均值约为3.24,即调频噪声信号经过脉压滤波器后的幅度增益约为3.24。

基于概率密度函数,以下将分析干扰的参数与干扰评估指标的具体关系,包括干扰与信号的带宽比、干扰的频率引导误差及干扰与信号的幅度比。

图2中横坐标为噪声调频干扰带宽与线性调频脉冲压缩滤波器带宽的比值,纵坐标为“等效视数”,参数δf=0,Uj=0。从图2可知,带宽比值为0.4时“等效视数”出现极大值,称为“随机共振”现象[5,10]。

图1　典型概率密度函数曲线　　　图2　ENL与带宽比的关系

图3中横坐标为干扰频率引导误差δf,纵坐标为“等效视数”,参数Bj/B=1,Uj=0。图中并无明显的极值点,实际实施干扰时引导误差应尽可能保证干扰频谱覆盖目标信号。

图4中横坐标为信号幅度归一化时的干扰幅度值,纵坐标为“等效视数”,参数Bj/B=1,δf=0。由图可知,干扰与信号幅度比为2时“随机共振”最强。当Bj/B=0.5或2、δf=0时,Uj/U0与虚警概率pfa的关系如图5。

进一步考察干扰与信号带宽比和幅度压制系数的关系,取虚警概率pfa=0.1和pfa=0.9时,带宽比Bj/B与幅度压制系数Ka的关系如图6。

图6给出了幅度压制系数、干扰和信号的带宽比及虚警概率三者之间的关系。由图可知,不同的虚警概率下,带宽比大于1时,带宽比与幅度压制系数近似成线性关系。带宽比越大则幅度压制系数越大,即输入干信幅度比越大。

图3　ENL与频率引导误差的关系　　　图4　ENL与干扰幅度的关系

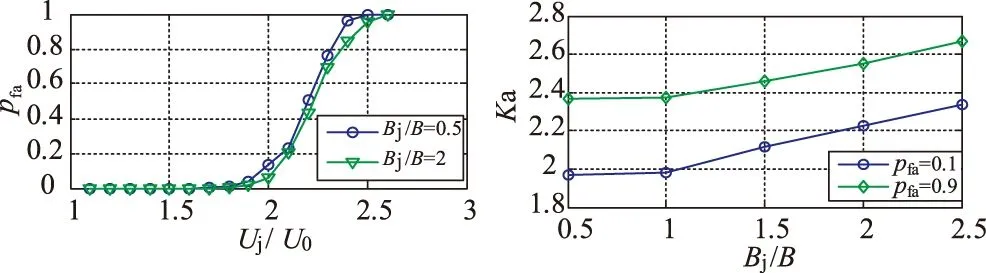
图5　典型参数下的虚警概率曲线　　　图6　幅度压制系数与带宽比的关系

上述的多组仿真都是基于特定雷达参数条件下,结果表明干扰参数带宽、幅度和频率引导误差均对脉压滤波器输出的干扰效应产生不同的影响。结束语

本文深入研究脉压雷达匹配滤波器信号处理过程,以ENL和幅度压制系数为指标,定量分析了宽带噪声调频干扰对脉压滤波器的干扰机理,并给出特定参数下的仿真结果,对干扰机设计具有一定的参考价值。后续的研究将进一步对脉压雷达其他关键的信号处理过程,如恒虚警检测、动目标检测等进行一般压制式干扰的效应评估,具体量化各种压制干扰对脉压雷达的干扰效应。

参考文献:

[1]宋春江,张剑云.噪声干扰对线性调频脉冲压缩滤波器的干扰效果分析[J].电子对抗技术,2000,15(5):l-10.

[2]李敬勇.对线性调频脉冲压缩雷达干扰的时域分析[J].电子对抗技术,1998,13(3):15-20.

[3]刘阳,王雪松,李永祯.噪声调频信号对宽带调频雷达的干扰机理[J].现代雷达,2008,30(10): 52-56.

[4]高建卫,魏青,杨绍全.噪声调频信号对合成孔径雷达的干扰[J].航天电子对杭,2004,20(4): 16-19.

[5]贺静波.基于随机微分的噪声干扰信号处理方法及其应用研究[D].武汉:华中科技大学,2009.

[6]HeJing-bo,HuSheng-liang.TheStochasticResonanceofNoiseFrequencyModulationSignalUsingMotion-GroupFourierTransform[C]//AppliedMechanicsandMaterials,2015: 1452-1455.

[7]赵国庆.雷达对抗原理[M].2版.西安: 西安电子科技大学出版社,2012: 135-138.

[8]WangY,ZhouY,MaslenDK,etal.Solvingphase-noiseFokker-Planckequationsusingthemotion-groupFouriertransform[J].IEEETransactionsonCommunications,2006,54(5): 868-877.

[9]WangY.ApplicationsofDiffusionProcessesinRobotics,OpticalCommunicationsandPolymerScience[D].Boltimore:TheJohnsHopjinsUniversity,2001.

[10]ChizhevskyVN,GiacomelliG.Improvementofsignal-to-noiseratioinabistableopticalsystem:Comparisonbetweenvibrationalandstochasticresonance[J].PhysicalReviewA,2005,71(1).

Jamming mechanism of wideband noise FM signals to pulse compression

SUN Qing-qing1,2, ZHENG Kun1, CAO Xu-yuan1, WANG Hong2

(1. Key Laboratory of Electronic Information Control, Chengdu 610036; 2. School of Electronic Engineering,University of Electronic Science and Technology of China, Chengdu 611731)

Abstract:The effect of the jamming on radar signal processing is studied, which has a significant impact on the design of the jammer. In order to analyze the jamming effect of the wideband noise FM signals to the pulse compression filter, the stochastic differential theory is introduced, and the Fokker-Planck equations of the FM noise jamming signals are established. The calculation results indicate that the jamming signals output the probability density distribution function of the time-domain envelop via the pulse compression filter. Based on the distribution function output by the jamming signals, with "equivalent number of looks" and the amplitude suppression coefficient as the evaluation indexes of the jamming effect, the effect of the bandwidth, amplitude and frequency guiding error of the noise FM jamming signals on the jamming effect is simulated and analyzed.

Keywords:jamming mechanism; pulse compression; noise FM jamming; stochastic differential

收稿日期:2015-12-18;修回日期:2015-12-25

基金项目:国防基础科研基金项目(B1120133036);电子信息控制重点实验室基金项目

作者简介:孙清清(1990-),男,硕士研究生,研究方向:雷达信号处理、高速实时信号处理;郑坤(1982- ),男,高级工程师,博士,研究方向:电子对抗技术、雷达信号及数据处理;曹旭源(1987- ),助理工程师,硕士,研究方向:雷达干扰技术、数字信号处理技术;王洪(1974-),男,副教授,博士,研究方向:雷达信号处理、ADS-B、多点定位、数字接收机和高速实时信号处理。

中图分类号:TN97

文献标志码:A

文章编号:1009-0401(2016)02-0030-05