采用无差动滚齿确定挂轮定数
马跃峰,赵杏根,刘 义
(晋中经纬钰鑫机械有限公司,山西 晋中 030601)
•专家答疑
采用无差动滚齿确定挂轮定数
马跃峰,赵杏根,刘义
(晋中经纬钰鑫机械有限公司,山西 晋中030601)
摘要:为了解决采用无差动装置滚齿机加工小螺旋角齿轮,加工原理、公式推导过程欠缺的问题,详细演示了其加工参数的计算推导过程;通过实例说明采用无差动装置滚齿机加工螺旋齿轮参数的计算及挂轮定数的确定。指出:当齿轮螺旋角太小、差动挂轮速比大于1∶6时,或螺旋齿数为质数齿、齿数大于100齿时,都可采用无差动挂轮滚齿,利用推导公式进行挂轮调整,加工效果良好。
关键词:无差动装置;挂轮;螺旋角;推导公式;滚齿机
0引言
滚齿机的传动机构主要有两种:一种有差动装置,一种无差动装置,当斜齿轮螺旋角太小、差动挂轮速比大于1∶6时,就无法使用差动挂轮;这时可以用无差动装置滚齿机加工(也适用于质数齿螺旋齿轮)。生产中常遇到小螺旋角齿轮的加工,采用无差动装置滚齿机加工取得了很好的效果,解决了加工螺旋齿轮的难题。
虽然,大量的技术资料中都有关于无差动装置滚齿机加工参数的计算公式,但是公式的来源和推理却没有详细地报道[1-3]。笔者将详细介绍无差动装置滚齿机的加工原理、过程和计算公式的推导,以供工艺技术员、齿轮工参考。
1有差动滚齿机作无差动滚齿机使用
无差动滚齿机或未用差动装置的有差动装置滚齿机,如图1所示;当加工螺旋齿轮时,会出现差动蜗杆脱开、交换齿轮锁死的问题。
当主轴1传动伞齿轮A滚切直齿时,可以不用差动装置;当把齿轮D端的凸键插入齿轮C端内,再把轴14的蜗杆与差动装置的蜗轮C脱开,使差动装置成为一体;当轴2转动时,直接传动到轴1使差动装置不产生作用,就没有了差动挂轮比。因为在这种情况下加工螺旋齿轮必须依靠分齿挂轮和进刀挂轮配合完成,所以这两个挂轮比的计算就和正齿轮不同。

1—齿轮A;2—齿轮B;3—蜗轮C;4—齿轮D;5—蜗杆轴14。图1 无差动装置的滚齿机
当用右旋滚刀滚切右旋斜齿轮时,图2中AB为齿轮展开尺寸,Ft为垂直进刀量,理论上滚刀从A点至E点应切完一圈;但由于斜齿轮的关系,切削并未完成,必须使齿轮旋转延长至D才能完成切削。

图2 右旋滚刀滚切右旋斜齿轮示意
那么,当滚刀旋转z/a转时,工作台必须旋转AD/AE,但AD/AE=AC/AB;又因AB=πd节,则:
(1)
(2)
如果把左右旋齿轮都进行考虑,则式(2)变为:
(3)
式中:
z——齿轮齿数;
d节——节圆直径;
a——滚刀头数。
如图2所示,垂直进刀有两种情况:当滚刀旋转z/a转时,垂直进刀量为Fh;当工作台旋转1周时,垂直进刀量为Ft。将图2局部放大为图3,Fh、Ft为垂直进刀量,α为螺旋角。




图3 垂直进刀



式中:
a1、d1——分齿交换齿轮;
c′——分齿挂轮定数;
c′=24,与前同样,c′不等于c。

式中:
tn——齿轮周节,tn=πmn;
mn——齿轮法向模数。
代入:a1/b1=24ac/(zc∓1)
因为分齿挂轮:
式中:
PL=πmn/sinα(轴向节距PL)
c(取整数)=PL/Ft(c为计算系数)

仿德的Y37型:滚齿机分齿挂轮定数c′=24,垂直进刀定数为9/32。
2生产实例
在Y37型无差动装置的滚齿机上滚螺旋齿轮,见传动图4(利用上述公式计算Y37型无差动滚齿机分齿运动链方程和垂直进刀运动链方程从略)。
2.1例一
加工一个圆柱螺旋齿轮(磨滚刀刃口用靠模),螺旋角α=1°18′(左旋),模数m=4mm,z=14mm、

图4 Y37型无差动滚齿机示意
进刀量S垂=1mm,滚刀头数a=1,试求各组挂轮?
分析:该齿轮螺旋角太小,差动挂轮速比小于1∶6,不能用差动挂轮滚齿;故应采用无差动滚齿,现用公式计算如下:




式中:
πmn——法向周节;
c——计算用系数。
进刀向上走。
2.2例二
有一个8级精度的螺旋齿轮,齿宽=40mm、模数=2.5mm、齿数=28、螺旋角α=15°30′(左旋)、S垂=1mm,滚刀用单头右旋,试求各组挂轮?
解:① 计算齿轮的轴向节距PL
PL=πmn/sinα=28.85(mm)
c=PL/1≈29


③ 进刀挂轮:


2.3例三
有一个质数螺旋齿轮,模数mn=1.75mm、齿数z=103、螺旋角α=11°30′(右旋)、进刀S垂=1mm、滚刀用单线右旋,试求各组挂轮?
解:① 计算齿轮的轴向节距PL
所以c=PL/S垂≈28(取整数)
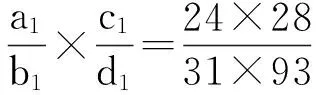

如图4所示,Y37型无差动滚齿机S垂进刀系的轴连接在工作台分齿交换齿轮之后,与Y38型滚齿转动相似,如要求Y37型分齿运动链方程和垂直进刀运动链方程,可参考Y38型滚齿机运动方程计算求知。
3结语
3.1当齿轮螺旋角太小(差动挂轮速比太大)时,用差动挂轮滚齿不现实,故应采用无差动滚齿,利用推导公式进行挂轮调整,加工效果良好。
3.2当螺旋齿轮为质数齿时,齿数大于100齿则分度挂轮无交换齿轮,同样可用无差动挂轮滚齿,如例3,103齿的齿轮已批量生产。
3.3式中“+”为滚刀与加工齿轮螺旋角同方向,“-”时为滚刀与加工齿轮螺旋角反方向。
参考文献:
[1] 北京业余机械学院工人班.齿轮原理与制造[M].北京:科学出版社,1970.
[2] 天津齿轮机床研究所.齿轮手册[M].天津:天津科学技术出版社,1979.
[3] 熊万武.挂轮选用表[M].北京:机械工业出版社,1968.
Determination of Gear Change Number Using Non-differential Hobbing
MA Yuefeng,ZHAO Xinggen,LIU Yi
(Jinzhong Jingwei Yuxin Machinery Co.,Ltd.,Jinzhong 030601,China)
Abstract:In order to solve the problems with the production of gear with small spiral angle using the non-differential hobbing machine,the processing principle and formula derivation,a detailed presentation is given of the processing parameters of the calculation process.The example shows how to make determination of gear change number using non-differential hobbing for spiral gears.It is pointed out that when the gear spiral angle is too small and the differential hanging wheel speed ratio is greater than 1∶6,or helical teeth number is of prime number and the teeth number is greater than 100 teeth,non-differential gear hobbing is employed,using the derived formula regulating the hanging round with good processing effect.
Key Words:non-differential devices;gear change;spiral angle;derived formula;gear hobbing machine
收稿日期:2015-09-21
作者简介:马跃峰(1959—),男,山西榆次人,工程师,主要从事纺织机械制造及工艺、工装、改造设计等工作。
中图分类号:TS103.7+4
文献标志码:B
文章编号:1001-9634(2016)03-0018-03

