起伏地表频域/时域航空电磁系统三维正演模拟研究

张博, 殷长春, 刘云鹤, 蔡晶

吉林大学地球探测科学与技术学院， 长春　130026

起伏地表频域/时域航空电磁系统三维正演模拟研究

张博, 殷长春*, 刘云鹤, 蔡晶

吉林大学地球探测科学与技术学院， 长春130026

摘要由于航空电磁系统具有工作频率低、时间延迟短等特点，地形对航空电磁响应有很大影响，忽略地形影响会给航空电磁数据解释造成很大误差.本文将基于非结构化网格的矢量有限元法应用于模拟起伏地表条件下频域/时域(FD/TD)三维航空电磁系统响应.该方法由于采用非结构网格，与传统的结构化网格电磁正演算法相比，能更好地拟合地形和地下不规则异常体，提高对不规则地形和地下介质航空电磁响应的计算精度.通过将计算结果与半空间模型的半解析解及已发表的结果进行对比，检验了本文算法的精度.通过对典型山峰和山谷地形航空电磁响应分析对比，总结了地形对航空电磁响应的影响特征.研究结果对航空电磁地形效应的识别和校正具有指导意义.关键词航空电磁； 三维正演； 地形效应； 矢量非结构有限元法

Starting from the frequency-domain Maxwell′s equations, we obtain a vector Helmholtz equation for a stable solution when air is present. We use the Galerkin method to discretize the Helmholtz equation and obtain the final finite-element equations. To accelerate the calculation speed, the source response in a free-space is used as the primary field, while the direct solver is used to deal with the multiple-source problem. After calculating the frequency-domain AEM responses, a Hankel′s transform is applied to obtain the time-domain EM responses.

To check the accuracy of the presented algorithm for AEM topographic modeling,we compare our results with both the semi-analytical results and those from published literatures.After that, we calculate the EM responses for 3D models with only topography and with both topography and anomalous targets.

From profiled AEM responses, we draw similar conclusions to those of Yin (2015), while from area AEM responses, we find that: 1) for frequency-domain AEM systems, the real part of AEM response contains more information to deep earth than the imaginary part; 2) for time-domain AEM system, the magnetic induction dB/dtreveals the underground conductivity distribution better than theBfield. These features provide the theoretical basis for identification and correction of topographic effect from the AEM measurements.

1引言

航空电磁法由于其高效、经济、且无需地面人员接近勘查区等特点，在地质填图、油气勘探、矿产普查及工程和环境调查等方面得到了广泛的应用(Wolfgram and Goiden, 2001; Paine and Collins, 2003;Smith et al., 2006; Pfaffhuber et al., 2009;Tan et al., 2009; Yang and Oldenburg, 2013).国内外众多学者研究表明，地形效应对航空电磁响应的影响巨大(Liu and Becker, 1992; Annetts et al.，1998；Mitsuhata, 2000; Baba and Seama, 2002; Sasaki and Nakazato, 2003; Nam et al.，2007；刘云鹤和殷长春，2013；蔡晶等，2014).忽略这种影响会给航空电磁数据解释带来很大误差(殷长春等,2015).然而人们对带地形条件下频/时域三维航空电磁响应的研究还十分有限.传统的有限差分、积分方程和基于规则网格的有限元法已经被广泛应用于解决三维航空电磁正演模拟问题(Newman and Alumbaugh，1995；Avdeev et al.，1998)，然而这些方法往往采用矩形或长方体对模型进行剖分，在处理不规则地形或地下复杂异常体时往往需要将网格剖分得很细，浪费计算资源，且拟合地形效果不佳.近年，一些学者使用非结构网格对电磁正演问题进行的研究主要集中在海洋电磁领域(Um et al., 2010;Ren et al.，2014; Fu et al., 2015)，采用非结构化网格对起伏地表条件下三维频/时域航空电磁响应进行模拟的学者较少.由于航空电磁已经越来越广泛地应用于地球物理勘探，地形对航空电磁响应的影响十分巨大，本文将基于非结构网格的矢量有限元法应用于带地形条件下三维频/时域航空电磁系统响应正演模拟.

由于非结构网格能够有效剖分任意复杂地质模型，其在电磁正演模拟中的应用比传统的结构化网格和二叉树网格更加广泛.本文采用体积和质量约束的Delauany四面体剖分技术对计算区域进行网格剖分.由于对Maxwell方程进行直接求解会出现解不稳定的问题，我们使用电场的Helmholtz方程进行问题求解.一次/二次场分离算法与直接计算总场算法相比具有更高的计算精度和更好的稳定性，因此本文采用分离算法对航空电磁响应进行模拟.我们使用Galerkin方法对Helmholtz方程进行离散，得到三维航空电磁正演问题对应的数学方程.由于航空电磁具有多源性，我们采用直接分解技术对矩阵方程进行求解.在得到不同频率的航空电磁响应后，我们对频率域响应进行汉克尔变换，从而得到时间域航空电磁响应.

我们首先通过对比本文计算结果与半空间模型的解析解以及其他已发表的结果检验算法的精度.然后，我们针对典型山峰和山谷地形模型计算航空电磁响应，分析纯地形模型航空电磁响应特征.为了进一步分析地形对航空电磁系统响应的影响，我们还计算和分析了地形模型中埋藏异常体模型的电磁响应.

2正演算法

电磁场在发射源附近变化非常剧烈，使用直接计算总场方法进行正演模拟时，为保证正演精度，必须将源附近的网格划分得很细，浪费大量的计算资源.一次场二次场分离算法将异常体看成虚拟源以代替真实源，从而避免了真实发射源附近场值变化剧烈的问题.然而，理论研究表明，一次场二次场分离方法不适合处理背景场难以获得的复杂地电模型(Mitsuhata, 2000; Jahandari and Farquharson, 2014)，这是由于获得背景场耗费的计算资源十分巨大.此外，该方法必须将起伏地表看成异常体，当发射源或接收点位于起伏地表附近时，发射源和接收点附近的起伏地表必须被划分成很密的网格以保证求解精度.由于航空电磁收发装置距离地面有一定的飞行高度，因此无需将起伏地表网格划分得很密.另外，由于该方法对于任意复杂模型均可使用源在全空间的响应作为背景场，能大幅度减少背景场计算工作量.从以上分析可以看出，一次场二次场分离算法在处理航空电磁正演问题时保留了计算精度高、网格划分少的优点；同时避免了复杂模型背景场计算量大，对发射源和接收点附近的起伏地表网格要求剖分密等缺点.本文采用一次场二次场分离算法对三维航空电磁响应进行模拟.二次场满足如下形式的Maxwell方程：

(1)

(2)

式中σ是电导率，σs=σ-σp(σp是背景电导率)，Ep是背景电场，Es是待求解的二次场，μ是磁导率.直接求解(1)式和(2)式会出现解不稳定问题.由此，三维航空电磁通常对Helmholtz方程进行求解.从(1)和(2)式我们可以得到电、磁场满足的Helmholtz方程.我们利用电场的Helmholtz方程进行求解，即

(3)

为确保电场具有唯一解，本文对计算区域的外边界添加了Dirichlet边界条件：

(4)

式中Ω表示计算区域外边界，g表示二次场在边界处的场值.本文令计算区域的边界远离异常体，因此可以假设g=0.(3)和(4)式构成了二次电场对应的边值问题.

本文使用有限元法求解边值问题包括以下几个步骤：

1) 将计算区域离散成小单元；

2) 计算(3)式与形函数N的L2内积以得到边值问题对应的泛函形式(L2内积的定义见附录B)；

3) 计算上述边值问题的泛函，得到整体刚度矩阵；

4) 求解有限元方程，得到问题的解.

图1　矢量有限元四面体单元内电场分布Fig.1　Electrical fields in a tetrahedron element for vector FEM

我们首先使用Delaunay方法对计算区域进行四面体网格剖分.Delaunay网格的具体性质及剖分方法见附录A.为了保证网格剖分质量，对网格剖分添加了体积和质量约束.使用节点有限元法进行电磁场数值模拟存在严重的缺陷.首先,由于未强加散度条件，节点有限元法求解出来的场可能出现非物理解；其次，由于节点有限元法在介质分界面处求解出的场不具有连续性，在介质分界面处强加边界条件十分不便.矢量有限单元法由于将电场赋于棱边上, 并且其基函数在每个单元内自然满足散度条件，确保了电场在介质分界面处的连续性，从而克服了节点有限元的缺陷.本文选择的矢量有限单元每个单元中电场在棱边上的分布情况如图1所示.

对(3)式与基函数在每个小单元进行L2内积，并使用格林公式和分部积分，可以得到边值问题对应的变分形式.对变分形式的边值问题使用有限元方法进行离散，并将所有小单元对应的系数矩阵进行组合，我们可以得到形式如下的整体矩阵方程：

(5)

式中Es是棱边上的矢量电场，系数矩阵K是由每个单元对应的小矩阵K1和K2组成的对称稀疏非Hermitian矩阵，右端项向量b由每个单元对应的源项向量be=K3Ep组成.公式(5)的推导过程见附录B.

由于航空电磁的移动平台特征具有多源性，传统的迭代求解算法处理该问题时需要对每个源进行一次单独正演，计算速度慢.本文采用直接分解算法对(5)式进行求解.该方法针对模型不变的情况只需一次分解就能得到所有源对应的响应(Oldenburgetal., 2013)，求解效率较之于传统的迭代算法有很大提高.由式(5)求得棱边上的电场Es后，空间任意位置的磁场可由Faraday′s定律得到：

(6)

由(5)和(6)式计算出多个频率对应的航空电磁系统响应，针对本文发射的阶跃波信号，利用正弦变换(等价于0.5阶汉克尔变换)对频率域航空电磁响应进行反傅里叶变换：

(7)

(8)

式中t表示时间，J表示贝塞尔函数，ω为角频率.经过以上变换，我们可以由频率域航空电磁响应得到时间域航空电磁响应.

3精度验证

为了检验本文算法对三维航空电磁响应的模拟精度，我们将本文计算结果与Sasaki和Nakazato(2003)使用有限差分计算的起伏地表频率域航空电磁响应进行对比；对于时间域航空电磁响应，我们将本文的结果与半空间模型的半解析解进行对比.Sasaki和Nakazato(2003)计算的梯形山峰模型(简称模型一)及其网格划分情况如图2a所示.山峰高50m，顶部和底部分别宽20m和220m；模型的电阻率为100Ωm；收发装置采用水平共面装置，收发距10m，发射频率为16kHz，飞行高度固定为距离起伏地表30m.图2b给出了本文模拟结果与Sasaki和Nakazato(2003)模拟结果之间的对比，图2c给出两者之间的相对误差.从图中可以看出，两者吻合较好，最大相对误差不超过4%.

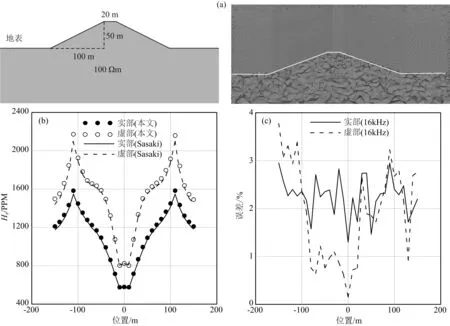
图2　本文模拟结果与Sasaki和Nakazato(2003)模拟结果对比(a) 山峰模型； (b) 模拟结果对比； (c) 相对误差.Fig.2　Comparison of results from this paper with those from Sasaki and Nakazato(2003) (a) A trapezoid hill model; (b) Comparison of the FE solution of this paper with those from Sasaki and Nakazato(2003); (c) Relative errors.

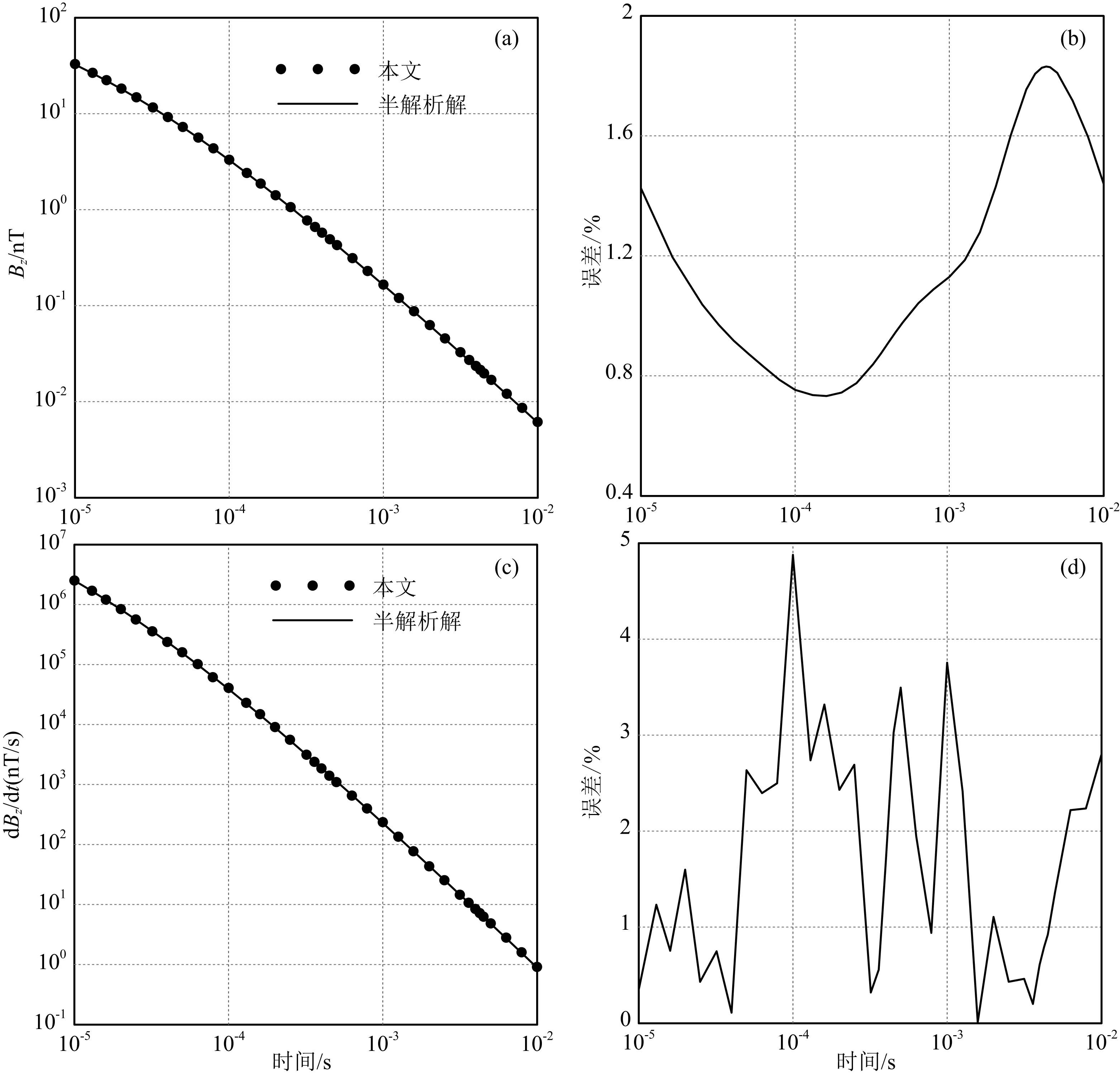
图3　本文模拟结果与半解析解对比(a) Bz模拟结果对比； (b) Bz相对误差曲线； (c)dBz/dt模拟结果对比； (d) dBz/dt相对误差曲线.Fig.3　Comparison of FE results from this paper with the semi-analytical results from Yin et al. (2013)(a) Comparison of time-domain Bz; (b) Relative errors for Bz; (c) Comparison of dBz/dt; (d) Relative errors for dBz/dt.

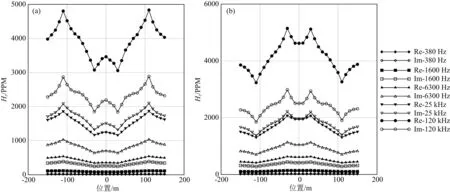
图5　纯地形模型频率域航空电磁测线响应(a) 模型二响应； (b) 模型三响应.Fig.5　Frequency-domain AEM responses in profile(a) EM responses for model 2； and (b) for model 3.

由于带地形模型时间域航空电磁响应发表的正演模拟结果较少，本文将计算结果与半空间模型的半解析解(殷长春等, 2013)进行对比.收发装置参考FUGRO系统，参数设置如下：发射高度30m，接收高度50m，发射、接收线圈的水平距离为10m，发射偶极矩为615000Am2，发射波形为阶跃波(下文所有时间域系统参数均相同).正演模拟结果对比如图3a和3c所示，相对误差如图3b和3d所示.从图中可以看出，B场最大误差不超过2%，dB/dt仅个别点相对误差在3%附近，整体相对误差不超过3%.由此我们得出结论：本文的正演模拟方法无论对频率域还是时间域均具有较高的计算精度.

4地形影响特征分析

下面我们通过模拟山峰和山谷地形频率/时间域三维航空电磁响应，分析地形对航空电磁响应的影响特征.山峰和山谷地形模型如图4a和4b所示(简称模型二和模型三).山峰高度和山谷深度均为20m，在顶部和底部的宽度分别为60m和220m，模型的电阻率为100Ωm.对于频率域航空系统，本文模拟了水平共面(HCP)装置380Hz, 1600Hz, 6300Hz, 25kHz, 120kHz五个频率的电磁响应，装置距离地表30m，收发距10m(下文所有频率域系统均与此相同).对于时间域航空电磁响应，本文模拟了FUGRO系统在10-5～10-2s之间12个时间道的航空电磁响应.由于在低频段和晚期，航空电磁正演响应受地形影响很小，本文的正演响应结果平面分布仅给出120kHz(高频)和1600Hz(中低频)以及10-5s(早期时间道)和3.2×10-4s(中晚期道)的结果，而对测线正演响应我们给出了全部12个时间道以及5个频率的计算结果.图5a和5b分别给出了模型二和模型三对应5个频率的电磁响应信号，测线位于模型中心剖面；图6和图7分别给出了模型二和模型三频率域航空电磁响应的平面分布；图8给出了模型二和模型三12个时间道电磁信号的响应，测线位于模型中心剖面；图9和10分别给出了模型二和模型三时间域航空电磁B和dB/dt的平面响应.

从图5、8的模拟结果和响应特征分析我们可以得出如下结论： (1) 地形对频率域和时间域航空电磁响应均有较大影响，航空电磁数据处理解释不能忽略地形效应； (2) 频率越高或时间道越早，电磁响应受地形的影响越大.这是因为高频段电磁信号穿透能力较弱，反映的信息主要来自距离航空电磁收发装置较近的地表介质；而低频段电磁信号穿透能力较强，反映的信息主要来自距离航空电磁收发装置较远的地下深部介质.由此也揭示了地形影响主要出现在高频段电磁信号中.与之相对应，早期道电磁信号反映的信息来自距离航空电磁收发装置较近的地表介质，而晚期道信号反映的信息主要来自离航空电磁收发装置较远的地下深部介质.因此，地形对早期时间道电磁信号影响较大； (3) 带地形航空电磁响应的曲线形态与地形之间存在镜像关系.在地形的拐点位置，电磁响应显示出剧烈的变化.从图6、7、9、10的模拟结果和响应特征分析我们可以进一步看出： (1) 对于同一频率的电磁信号，航空电磁响应的实部受地形影响小于虚部，而虚部则能够更好地刻画地形的形态，对精细结构的反应能力更强； (2) 对于同一时间道的电磁信号，B场受到地形的影响小于dB/dt场，而dB/dt场能够更好地刻画地形的形态，对精细结构的反映能力更强.这是由于磁场B是磁感应dB/dt的积分，在一定程度上平滑了异常电磁响应，使得地下(包括地形)精细结构的刻画能力受到减弱.

5地形对异常体响应的影响特征

为分析地形对异常体响应的影响，我们设计了山峰和山谷地形下埋藏低阻异常体的模型(简称模型四和模型五).模型四和模型五如图11a和11b所示.山峰和山谷模型参数与模型二和模型三参数相同，异常体埋在距离地表30m的位置，大小40m×

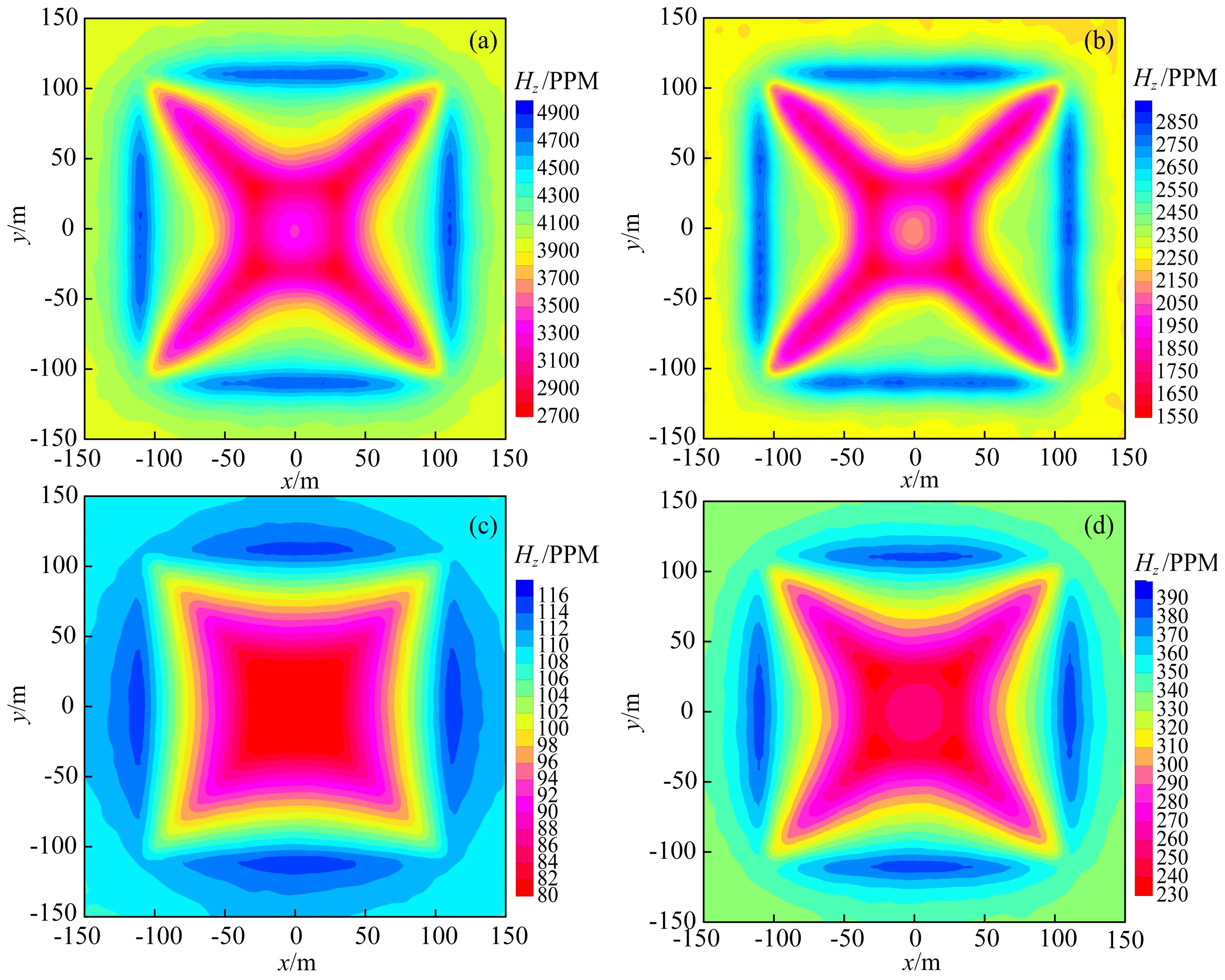
图6　模型二频率域航空电磁响应平面分布

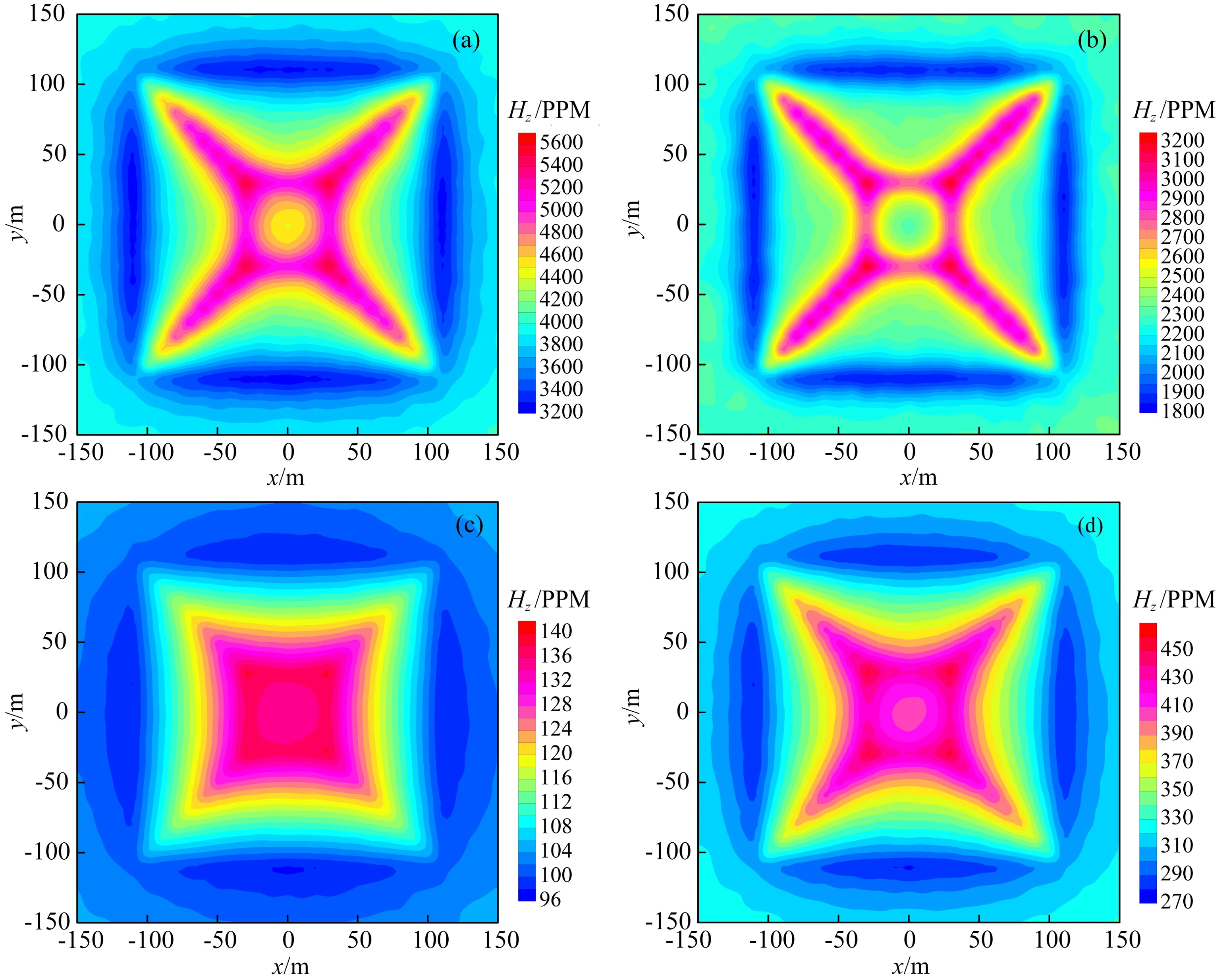
图7　模型三频率域航空电磁响应平面分布

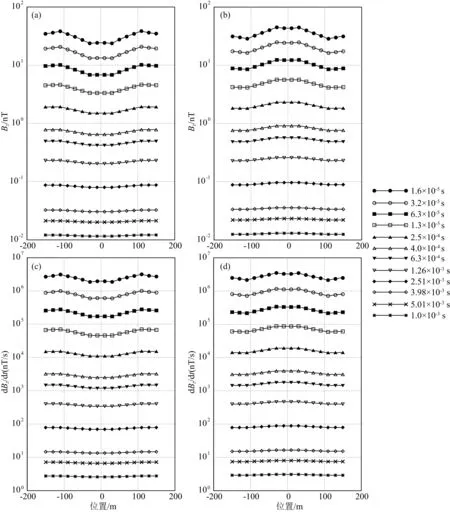
图8　时间域航空电磁测线响应(a) 模型二Bz响应； (b) 模型三Bz响应； (c) 模型二dBz/dt响应； (d) 模型三dBz/dt响应.Fig.8　Time-domain AEM responses in profile(a) Bz for model 2; (b) Bz for model 3; (c) dBz/dt for model 2; (d)dBz/dt for model 3.

40 m×30 m，电阻率为1 Ωm，围岩电阻率为100 Ωm.图12a和12b分别给出模型四和五5个频率的电磁响应信号.测线位于模型中心剖面，而图13和14分别给出了模型四和模型五频率域航空电磁的平面响应.图15给出了模型四和模型五12个时间道的电磁响应，测线位于模型中心剖面，而图16和17分别给出了模型四和模型五时间域航空电磁B和dB/dt的平面响应.

从图12、15的模拟结果和响应特征分析我们可以得到如下结论：纯地形与带地形异常体的响应曲线在高频段和早期时间道差异较小；然而，随着频率的降低或时间的延长，两者差异逐渐变大，地下电性不均匀体的影响突出表现出来.这从物理上很容易解释：在高频段和早期时间道，电磁信号穿透浅，主要反映地表信息，此时地形响应占主导地位，而异常体的响应微弱、难以识别；随着频率降低，或时间向晚期道推移，电磁信号逐步穿透地下介质，地表和地形响应减弱，而异常体的响应增强.由此，我们可以得出结论，地形效应主要体现在频域电磁信号的高频段或时域电磁信号的早期道，而有一定埋深目标体的电磁响应主要体现在中低频和中晚期时间道(取决于良导体导电性和埋深).

从图13、14、16、17中的模拟结果和响应特征分析我们可以进一步看出： (1) 对于频率域结果，高频信号的虚部刻画地形细节的能力强于实部，而低频信号的实部对具有一定埋深的异常体反映能力更强.以上现象表明，对于本文设计的模型，无论是高频信号还是中低频信号，频率域响应的实部包含的深部信息都较虚部丰富，而虚部则包含更多的浅层信息； (2) 对于时间域响应，无论是早期时间道信号刻画地形精细结构的能力，还是晚期时间道信号反映异常体的能力，dB/dt都强于B.这一现象再次说明dB/dt能够更好地刻画介质的电性变化特征.

图9　模型二时间域航空电磁响应平面分布(a) 10-5s的Bz响应； (b) 3.2×10-4s的Bz响应； (c) 10-5s的dBz/dt响应； (d) 3.2×10-4s的dBz/dt响应.Fig.9　Plane view of time-domain AEM response for model 2(a) Bz field at 10-5s; (b) Bz field at 3.2×10-4s; (c) dBz/dt at 10-5s; (d) dBz/dt at 3.2×10-4s.

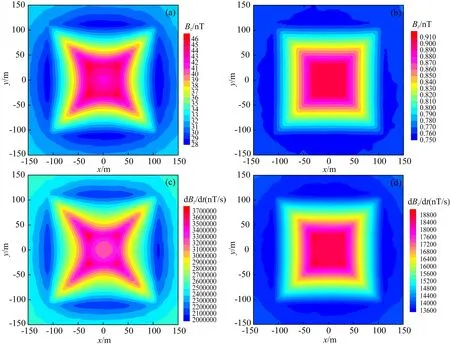
图10　模型三时间域航空电磁响应平面分布(a) 10-5s Bz响应； (b) 3.2×10-4s Bz响应； (c) 10-5s dBz/dt响应； (d) 3.2×10-4s dBz/dt响应.Fig.10　Plane view of time-domain AEM response for model 3(a) Bz field at 10-5s; (b) Bz field at 3.2×10-4s; (c) dBz/dt at 10-5s; (d) dBz/dt at 3.2×10-4s.

图11　带地形和异常体模型(a) 山峰模型(模型四)； (b) 山谷模型(模型五).Fig.11　An abnormal body under topography(a) An hill model (model 4); (b) A valley model (model 5).

图12　带地形和异常体模型频率域航空电磁响应(a) 模型四响应； (b) 模型五响应.Fig.12　Frequency-domain AEM responses in profile for (a) model 4 and (b) model 5

6结论

本文基于有限元方法能够模拟复杂模型，而非结构网格可以很好地模拟起伏地表的特点，成功将非结构矢量有限元法应用于模拟带地形条件下三维航空电磁响应正演模拟.通过与均匀半空间的半解析解及已发表模型结果进行对比，验证了本文算法具有较高的精度.通过选择使用源在全空间的解析解作为背景场，并采用直接分解求解器对矩阵方程进行求解，大大提高了正演计算速度.本文研究成果一定程度上为有效识别地形效应和异常体响应提供可能，对航空电磁数据解释在一定程度上提供了理论支撑.

通过大量理论模型的计算结果，我们得出如下结论：

(1) 对于频率域航空电磁系统，高频电磁信号虚部刻画地形细节的能力强于实部，而低频电磁信号实部反映具有一定埋深异常体的能力更强.由此我们可以合理推测，无论高频信号还是中低频信号，频率域航空电磁响应的实部包含的深部信息都较虚部丰富；

(2) 对于时间域航空电磁系统，早期时间道磁感应dB/dt刻画起伏地表细节的能力强于磁场B，而在晚期时间道dB/dt对异常体的反映能力较之于磁场B更强.因此，dB/dt对地质体电性分布变化更为敏感，在刻画异常体精细结构方面更具优势.

(3) 然而，由于地形和异常体响应处于相同数量级，为有效实现航空电磁数据反演解释，对地形影响进行模拟和校正十分必要.这将是我们未来的研究内容.

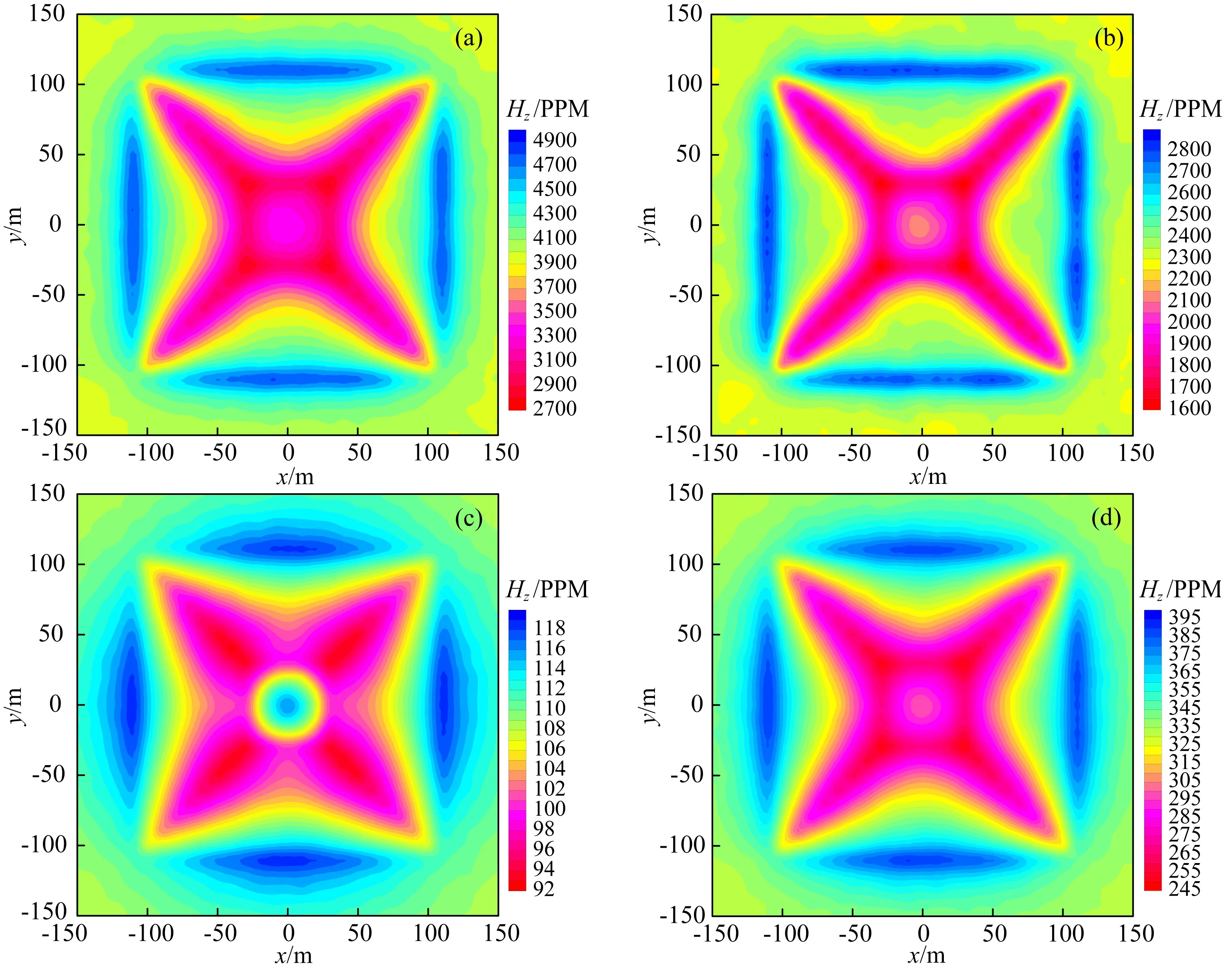
图13　模型四频率域航空电磁响应平面分布

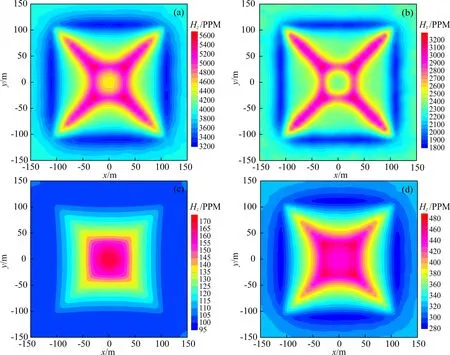
图14　模型五频率域航空电磁响应平面分布

图15　时间域航空电磁测线响应(a) 模型四Bz响应； (b) 模型五Bz响应； (c) 模型四dBz/dt响应； (d) 模型五dBz/dt响应.Fig.15　Time-domain AEM responses in profile(a) Bz for model 4; (b) Bz for model 5; (c) dBz/dt for model 4; (b) dBz/dt for model 5.

附录ADelaunay非结构网格性质及剖分方法

Delaunay四面体剖分方法能够得到高质量的四面体网格，目前已经成为电磁数值模拟中常用的一种网格剖分方法.Delaunay四面体剖分方法剖分网格具有如下性质：

(1) 空圆特性，即确保任意Delaunay四面体网格中任意四面体外接球范围内不会有其他点存在；

(2) 最大化最小角特性，即在散点集可能形成的四面体网格中，Delaunay四面体剖分所形成的四面体的最小角最大.性质1确保了划分网格的唯一性，并为网格剖分提供了一种依据，性质2确保了划分网格具有较高的质量.图A1比较了四个节点情况下Delaunay和非Delaunay网格剖分结果.图A1(a)中三角形BCD的外接圆将点A包含在内，因此剖分结果为非Delaunay网格；图A1(b)中三角形ABC和ACD的外接圆未将任何不属于三角形的节点包含在内，剖分结果为Delaunay网格.从图中我们可以看出Delaunay网格剖分比非Delaunay网格剖分具有更好的质量.

图A1　二维网格剖分示例(a) 非Delaunay网格； (b) Delaunay网格.Fig.A1　An example for 2D grids(a) General grids； (b) Delaunay grids.

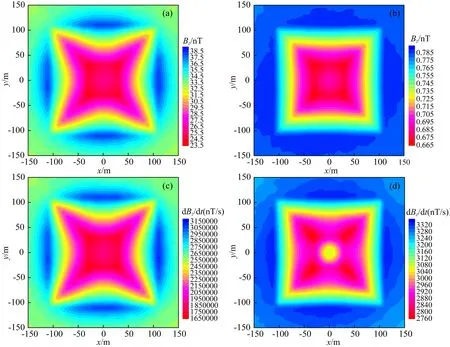
图16　模型四时间域航空电磁响应平面分布(a) 10-5s的Bz响应； (b) 3.2×10-4s的Bz响应； (c) 10-5s的dBz/dt响应； (d) 3.2×10-4s的dBz/dt响应.Fig.16　Plane view of time-domain AEM responses for model 4(a) Bz at 10-5s; (b) Bz at 3.2×10-4s; (c) dBz/dt at 10-5s; (d) dBz/dt at 3.2×10-4s.

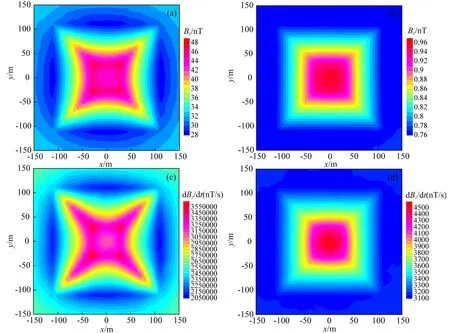
图17　模型五时间域航空电磁响应平面分布(a) 10-5s的Bz响应； (b) 3.2×10-4s的Bz响应； (c) 10-5s的dBz/dt响应； (d) 3.2×10-4s的dBz/dt响应.Fig.17　Plane view of time-domain AEM responses for model 5(a) Bz at 10-5s; (b) Bz at 3.2×10-4s; (c) dBz/dt at 10-5s; (d) dBz/dt at 3.2×10-4s.

基于性质1，我们给出一种Delaunay网格剖分方法如下(以二维情况为例)：

1) 构造一个大型辅助四边形，将空间所有节点包含在内；

2) 连接辅助四边形的一条对角线，形成两个大型三角形；

3) 将节点逐一插入辅助四边形内，若新节点的插入使某个三角形不再遵守性质1，则记录这个三角形，所有上述不遵守性质1的三角形构成了Delaunay腔；

4) 删除Delaunay腔内的已有三角形，将新插入的节点与Delaunay腔的顶点连接，得到腔内重新划分的网格；

5) 重复3—4步骤，直到所有节点被插入四边形内；

6) 删除与大辅助四边形有关的三角形单元，完成网格剖分.

附录B单元刚度矩阵推导

为方便下文推导，重写公式(3)：

(B1)

对(B1)式与基函数在每个小单元进行L2内积：

(B2)

并使用格林公式和分部积分，可以得到边值问题对应的变分形式：

∭ΩiωμσsNe·EpdΩ，

(B3)

(B4)

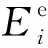
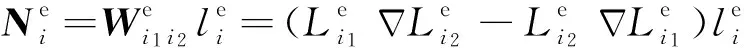
(B5)

式中L为标量有限元基函数，l表示棱边长度.从式(B5)中我们可以看出，矢量基函数自然满足散度为0条件.将(B4)式中的电场插值函数代入(B3)式，对于每个四面体单元我们可以得到

K1Es+K2Es=K3Ep，

(B6)

式中

(B7)

(B8)

(B9)

(B10)

将所有小单元对应的系数矩阵进行组合，我们可以得到形式如下的整体矩阵方程：

K Es=b.

(B11)

References

Annetts D, Sugeng F, Raiche A. 1998. The effect of topography on airborne electromagnetic response.∥ SEG Expanded Abstracts. New Orleans, Louisiana.Avdeev D B, Kuvshinov A V, Pankratov O V, et al. 1998. Three-dimensional frequency-domain modeling of airborne electromagnetic responses.ExplorationGeophysics, 29(2): 111-119. Baba K, Seama N. 2002. A new technique for the incorporation of seafloor topography in electromagnetic modelling.GeophysicalJournalInternational, 150(2): 392-402,doi:10.1046/j.1365-246X.2002.01673.x. Cai J, Qi Y F, Yin C C. 2014. Weighted Laterally-constrained inversion of frequency-domain airborne EM data.ChineseJournalofGeophysics(in Chinese), 57(3): 953-960, doi: 10.6038/cjg2014032.

Fu H H, Wang Y Q, Um E S, et al. 2015. A parallel finite-element time-domain method for transient electromagnetic simulation.Geophysics, 80(4): E231-E224, doi: 10.1190/geo2014-0067.1. Jahandari H, Farquharson C G. 2014. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids.Geophysics, 79(6): E287-E302, doi: 10.1190/geo2013-0312.1. Jin J M. 1998. Electromagnetic Finite-Element Method (in Chinese). Xi′an: Xidian University Press. Liu G M, Becker A. 1992. Evaluation of terrain effects in AEM surveys using the boundary element method.Geophysics, 57(2): 272-278, doi: 10.1190/1.1443240.

Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data.ChineseJ.Geophys. (in Chinese), 56(12): 4278-4287, doi: 10.6038/cjg20131230.

Mitsuhata Y. 2000. 2-D electromagnetic modeling by finite-element method with a dipole source and topography.Geophysics, 65(2): 465-475, doi: 10.1190/1.1444740.

Nam M J, Kim H J, Song Y, et al. 2007. 3D magnetotelluric modelling including surface topography.GeophysicalProspecting, 55(2): 277-287, doi: 10.1111/j.1365-2478.2007.00614.x. Newman G A, Alumbaugh D L. 1995. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences.GeophysicalProspecting, 43(8): 1021-1042.

Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data.Geophysics, 78(1): E47-E57, doi: 10.1190/geo2012-0131.1.

Paine J G, Collins E W. 2003. Applying airborne electromagnetic induction in groundwater salinization and resource studies, West Texas.∥ Symposium on the Application of Geophysics to Engineering and Environmental Problems. San Antonio, Texas, U.S.A., 722-738. Pfaffhuber A A, Monstad S, Rudd J. 2009. Airborne electromagnetic hydrocarbon mapping in Mozambique.ExplorationGeophysics, 40(3): 237-245, doi: 10.1071/ASEG2009ab040. Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2014. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling.Geophysics, 79(6): E255-E268, doi: 10.1190/geo2013-0376.1.

Sasaki Y, Nakazato H. 2003. Topographic effects in frequency-domain helicopter-borne electromagnetics.ExplorationGeophysics, 34(2): 24-28, doi: 10.1071/EG03024. Smith B D, Thamke J N, Cain M J, et al. 2006. Helicopter Electromagnetic and Magnetic Survey Maps and Data, East Poplar oil field area, August 2004, Fort Peck Indian Reservation, northeastern Montana. Open-File Report.Tan K P, Munday T, Halas L, et al. 2009. Utilizing airborne electromagnetic data to map groundwater salinity and salt store

at Chowilla, SA.∥ASEG Extended Abstracts 2009: 20th Geophysical Conference. ASEG, 1-6.Um E S, Harris J M, Alumbaugh D L. 2010. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite-element electric-field approach.Geophysics, 75(4): F115-F126, doi: 10.1190/1.3473694. Wolfgram P, Goiden H. 2001. Airborne EM applied to sulphide nickel-examples and analysis.ExplorationGeophysics, 32(4): 136-140.

Yang D K, Oldenburg D W. 2013. 3D conductivity models of Lalor Lake VMS deposit from ground loop and airborne EM data sets.∥23rd International Geophysical Conference and Exhibition. Melbourne, Australia: ASEG, 1-4. Yin C C, Huang W, Ben F. 2013. The full-time electromagnetic modeling for time-domain airborne electromagnetic systems.ChineseJ.Geophys. (in Chinese),56(9):3153-3162,doi:10.6038/cjg20130928. Yin C C, Zhang B, Liu Y H, et al. 2015. 2.5-D forward modeling of the time-domain airborne EM system in areas with topographic relief.ChineseJ.Geophys. (in Chinese), 58(4): 1411-1424, doi: 10.6038/cjg20150427.

附中文参考文献蔡晶, 齐彦福, 殷长春. 2014. 频率域航空电磁数据的加权横向约束反演. 地球物理学报, 57(3): 953-960, doi: 10.6038/cjg2014032. 金建铭. 1998. 电磁场有限元方法. 西安: 西安电子科技大学出版社. 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究. 地球物理学报, 56(12): 4278-4287, doi: 10.6038/cjg20131230. 殷长春, 黄威, 贲放. 2013. 时间域航空电磁系统瞬变全时响应正演模拟. 地球物理学报, 56(9): 3153-3162, doi: 10.6038/cjg20130928. 殷长春, 张博, 刘云鹤等. 2015. 2.5维起伏地表条件下时间域航空电磁正演模拟. 地球物理学报, 58(4): 1411-1424, doi: 10.6038/cjg20150427.

(本文编辑胡素芳)

3D modeling on topographic effect for frequency-/time-domain airborne EM systems

ZHANG Bo, YIN Chang-Chun*, LIU Yun-He, CAI Jing

CollegeofGeo-explorationSciencesandTechnology,JilinUniversity,Changchun130026,China

AbstractAirborne electromagnetic (AEM) exploration is an effective geophysical tool, especially suitable for survey in ridged mountain areas. Theoretical research shows that topography has serious effect on airborne EM responses. Negligence of this effect may create large errors in AEM interpretations. However, until now little study has been done on 3D topographic effect on frequency-/time-domain(FD/TD) airborne EM systems. Most scholars dealt with this problem using a structured grid that can′t simulate topography accurately. We present analgorithm using edge-based unstructured finite-element method(FEM).

KeywordsAirborne EM; 3D forward modeling; Topographic effect; Unstructured vector finite-element method

基金项目国家自然科学基金重点和面上项目(41530320，41274121)，国家青年基金项目(41404093)，国家重大科研装备研究项目(ZDYZ2012-1-03，20130523MTEM05)联合资助.

作者简介张博，1989年生，男，博士生，主要从事航空电磁正反演方面的研究. E-mail:em_zhangbo@163.com *通讯作者殷长春， 1965年生，男，教授，主要从事电磁勘探理论，特别是航空和海洋电磁方面的研究. E-mail:yinchangchun@jlu.edu.cn

doi:10.6038/cjg20160431 中图分类号P631

收稿日期2015-09-11，2015-11-06收修定稿

张博, 殷长春, 刘云鹤等. 2016. 起伏地表频域/时域航空电磁系统三维正演模拟研究.地球物理学报，59(4):1506-1520,doi:10.6038/cjg20160431.

Zhang B, Yin C C, Liu Y H, et al. 2016. 3D modeling on topographic effect for frequency-/time-domain airborne EM systems.ChineseJ.Geophys. (in Chinese),59(4):1506-1520,doi:10.6038/cjg20160431.