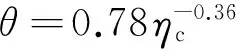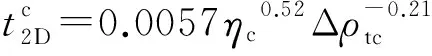克拉通岩石圈对流减薄的数值模拟

程华冬， 黄金

1 中国科学技术大学地球和空间科学学院地震与地球内部物理实验室， 合肥　230026 2 蒙城地球物理国家野外科学观测研究站， 合肥　230026

克拉通岩石圈对流减薄的数值模拟

1 中国科学技术大学地球和空间科学学院地震与地球内部物理实验室， 合肥230026 2 蒙城地球物理国家野外科学观测研究站， 合肥230026

摘要采用二维有限元数值模拟的方法研究了岩石圈的对流减薄过程，特别是克拉通岩石圈的对流减薄过程.模型的主要参数包括增厚岩石圈的宽度x、增厚倍数γ、以及与岩石圈组分变化导致的黏性和密度变化密切相关的黏性比(ηc)和浮力数(B)或等效密度变化(Δρtc).数值计算结果显示，地幔对流将逐渐减薄增厚的岩石圈部分，(1)当B=0和ηc=1时，即对一般地幔岩石圈，增厚岩石圈对流减薄的时间可表示为0.0073γ0.70x0.26.将数值结果应用于地球，意味着增厚到300 km的岩石圈，如宽度为300 km，对流移除增厚部分回到初始平衡厚度120 km大约需要225 Ma；如宽度为1500 km，移除增厚部分大约需要342 Ma.(2)当B和ηc较小，克拉通岩石圈对流减薄过程与一般加厚岩石圈的对流减薄过程类似，但减薄时间受克拉通组分浮力和黏性比的影响而显著增长，克拉通岩石圈对流减薄的时间可表示为γ0.78ηc-0.36x0.04.因而，对300 km厚的克拉通岩石圈，如克拉通岩石圈的密度比周围地幔的密度低0.4%(即B=0.1)，宽度1500 km，若克拉通岩石圈黏性因组分影响比普通地幔岩石圈大10倍，其被对流减薄到120 km大约需要1.18 Ga.(3)当B和ηc增大到一定量时(如B≥0.2且ηc>10)，克拉通岩石圈被移除的过程将发生变化，由于组分浮力的影响，对流主要不是将克拉通岩石圈带到软流圈地幔中，而主要是将较厚的岩石圈物质向两边推送.在此情况下，克拉通岩石圈能长时间(>3 Ga)保持稳定.

关键词克拉通岩石圈； 岩石圈减薄； 岩石圈减薄移除时间

1引言

克拉通是大陆上相对稳定的构造单元，包括地壳和岩石圈地幔(Rudnick and Fountain, 1995;Schubert et al., 2001).地质、地球物理和地球化学研究显示：克拉通有200多公里的岩石圈根，有的厚达300到400 km；克拉通区域表面热流值小；岩石圈根相对较冷、含水量低，并且显示出是部分熔融分异后的残留物；岩石圈根的密度相对较小、黏性较高；克拉通形成后可长期保持稳定，有的可长达40亿年(Boyd et al., 1985;Carlson et al., 2005;King, 2005;Pearson, 1999;Pearson et al., 1995).但是有些克拉通(如美国的Wyoming克拉通、我国的华北克拉通)在其形成后遭遇过改造(Carlson et al., 2004;Gao et al., 2002).其中华北克拉通是目前研究最为广泛和深入的地区.在华北克拉通发现了38亿年的陆壳残留物(Liu et al., 1992).在经历了早元古代(约25—18亿年间)的增生聚合碰撞事件后随着岩石圈厚度增大,华北克拉通作为一个完整的大陆块体长时期处于相对稳定的状态(Zhao et al., 2001).金伯利岩研究显示约在早古生代(～4.6亿年前)华北克拉通地幔岩石圈根的厚度约为200 km(路凤香等, 1991).大约在中侏罗世(～1.6亿年)中国东部开始大规模火山喷发.目前的初步研究认为华北克拉通岩石圈减薄发生在晚中生代，在早白垩世(1.2—1.3亿年)达到高潮，岩石圈的厚度从200 km减薄到80～120 km左右.伴随着这一过程，大量的火山活动使地幔岩石浸入地壳，地壳运动非常活跃，导致古老的华北克拉通的解体或破坏(Griffin et al., 1998;Menzies et al., 1993;Wu et al., 2005;Xu, 2001;邓晋福等, 2003;范蔚茗和Menzies, 1992;李江海等, 2004;邵济安等, 2002;吴福元等, 2003;许文良等, 2004;赵越等, 2004).

尽管目前对造成克拉通岩石圈减薄的机制和过程仍有许多争论，但普遍认为对流减薄在克拉通岩石圈减薄过程中具有重要影响.克拉通岩石圈减薄的概念性模型包括拆沉、对流侵蚀、热侵蚀、橄榄体和熔体的相互作用、岩浆提取、岩石圈地幔水化、以及机械拉张等(吴福元等, 2008).不同机制导致的岩石圈减薄后的后果和地表反应存在区别(吴福元等, 2008;朱日祥等, 2012).各种概念模型都有相应的地质、地球物理和地球化学观测等数据支撑(Carlson et al., 2005;Duggen et al., 2003;King, 2005;Schurr et al., 2006;Zhao and Zheng, 2007;吴福元等, 2008;许文良等, 2004).但对华北克拉通，目前的研究结果显示，由于岩石圈俯冲的影响，华北克拉通区域及其下覆地幔受到影响，软流圈地幔和岩石圈地幔的相互作用是导致华北克拉通被破坏的主因(朱日祥等, 2011, 2012).因而研究软流圈地幔对流对岩石圈地幔的影响具有重要意义(朱日祥等, 2012).

研究地幔对流对岩石圈的影响一直是地球动力学研究所关心的话题(Buck and Toksöz, 1983;Davies, 1994;Houseman et al., 1981;Huang et al., 2003;Marotta et al., 1999;Morency et al., 2002;Olson et al., 1988;Schott and Schmeling, 1998;Shapiro et al., 1999;Yuen and Fleitout, 1985;乔彦超等, 2012, 2013).数值模拟结果显示，加厚岩石圈减薄的过程和时间与模型参数密切相关.不同模型由于关注的对象不同，模型参数各异，导致得到的岩石圈减薄时间尺度变化很大，从～10 Ma(Marotta et al.,1999)到几百个Ma(Buck and Toksöz, 1983;Houseman et al., 1981)、甚至能够长期保持稳定(Shapiro et al., 1999).因而，定量研究加厚岩石圈的对流减薄和模型参数的关系，显得十分重要.

Morency等(2002)通过数值计算和理论分析的方法，定量分析了加厚岩石圈根在对流地幔中被移除的时间.其结果显示，加厚岩石圈根的移除时间与其大小(即其二维模型中的加厚岩石圈根的厚度和宽度)和黏性参数密切相关，并给出了估算公式.这对讨论增厚岩石圈的减薄过程及其对地表的影响等具有重要意义.然而在Morency等(2002)的模型中并未考虑克拉通地幔岩石圈和普通地幔岩石圈之间可能存在的由化学组分不同引起的密度和黏性差异，而这正是克拉通岩石圈和一般地幔岩石圈间的差异所在.现有研究都显示，克拉通岩石圈的密度和黏性差异对其稳定性具有重大影响(Lenardic and Moresi, 1999;Lenardic et al., 2003;O′Neill et al., 2008;Wang et al., 2014;Yoshida, 2012).因而本文将在Morency等(2002)的定量化方法的研究基础上，通过在数值模型中增加考虑由化学组分引起的岩石圈的密度和黏性变化的影响，进一步研究克拉通岩石圈在对流地幔中的减薄过程和减薄时间，为讨论克拉通岩石圈的对流减薄提供数值参考模型.

2数值模型

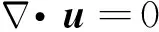
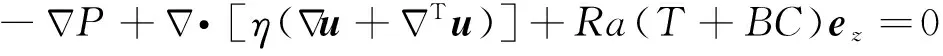
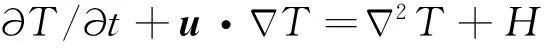
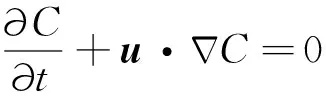
(1)

其中，u，P，η，T和H分别为流体速度矢量、压力、黏性系数、温度和内生热，C代表组分场，初始时刻，岩石圈内C=1，其余部分C=0.ez为z方向上的单位矢量，Ra为Rayleigh数，B是组分浮力数，其定义分别为：

(2)

其中，ρ0是地幔的参考密度，α是热膨胀系数，g是重力加速度，ΔT是模型上下边界温度差，D是模型深度，κ是热扩散系数，η0是底部边界的参考黏性，Δρc=ρ0-ρlith是组分密度差，ρlith指克拉通岩石圈的密度.方程组(1)无量纲化时的参数为：长度[L]=D；时间[t]=D2/κ；黏性[η]=η0；温度[T]=ΔT；内生热率[H]=(CpκΔT)/D2.

模型假定地幔黏性与温度相关，其无量纲形式为：

(3)

式中，E是无量纲的活化能，与活化能E*的关系：E=E*/(RΔT)，T0=Ts/ΔT是无量纲的表面温度，ηz表示黏性随深度的变化，这里主要用于表示软流圈.当无量纲化的深度Z<0.66时ηz=1/30，其他区域为ηz=1.ηc是组分黏性比，表示岩石圈组分变化导致的黏性变化.C=0的组分ηc=1，C=1的区域为岩石圈，通过改变ηc来模拟克拉通岩石圈的黏性变化.

数值模型是3×1的二维模型，方程(1)采用二维有限元程序Citcom解算.模型划分为289×97个有限单元网格，在靠近上下边界处，适度进行了网格加密.上表面给定温度，下表面热流为0，上表面固定，下表面和侧面边界自由滑移.本文模型深度取值1000 km，一方面能反映出软流圈与下地幔的黏性跳变，另一方面则是增大分辨率，模型选用的其他参数值见表1.根据(2)式，模型瑞利数Ra=1.3×107.由于我们研究的是拟稳状态下的对流模型，考虑到地球的冷却效应，为保证地幔温度保持大约1250 K，模型选取的内生热略大于地球内生热(Turcotte and Schubert, 2002).

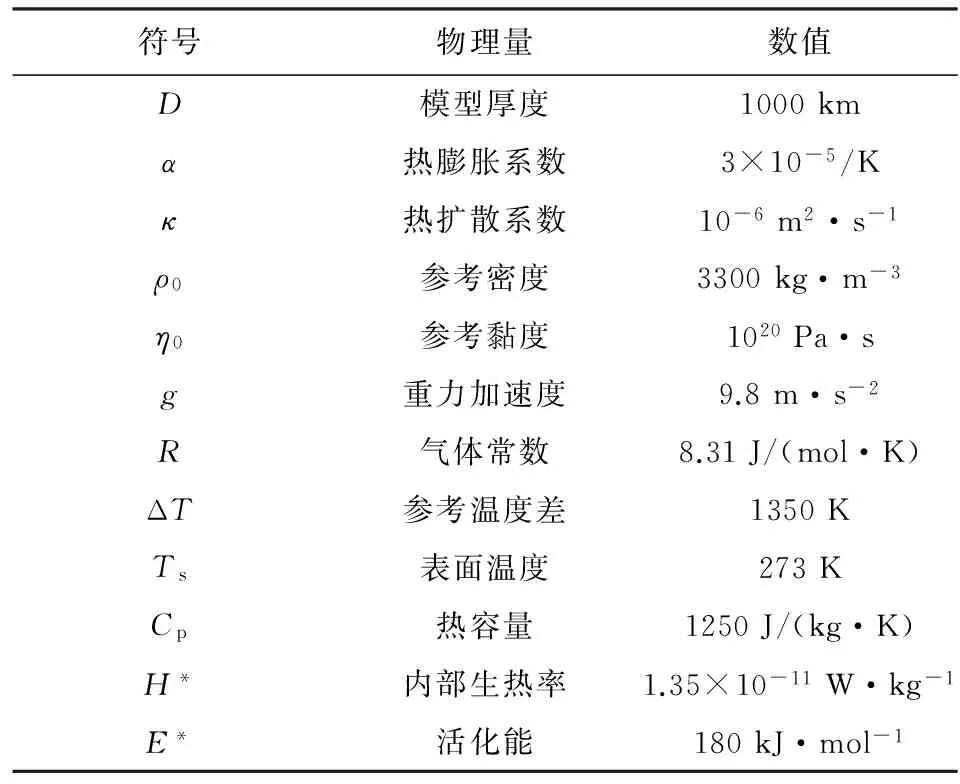
表1　模型参数值

为了定量研究克拉通岩石圈根的对流减薄时间，这里参考Morency等(2002)的做法，即：(1)首先计算一个参考模型，使其达到拟稳状态，此时模型的表面热流、内部温度以及均方根速度等基本保持不变.由于E很大，模型表现为近似刚性盖层下的小尺度对流形式(图1(a—d)).该边界层厚度，Zq，用以刻画岩石圈厚度，其值按横向平均温度T≤0.9Ti计算，Ti定义为无量纲模型深度在0.3到0.8之间的温度平均值.(2)克拉通岩石圈根通过增加参考模型局部区域岩石圈厚度来模拟(图1(e—h)).具体方法是在模型中部选取一定宽度(x)的区域将该区域厚度从Zq增加到Z0，Z0=(γ+1)Zq.由于边界层基本处于热传导状态，内部温度近似成线性关系，增厚边界层内的温度随深度的变化关系和增厚前一样，只是系数减小1/(γ+1).此时，增厚岩石圈相比于初始时，厚度增加了γZq，这里我们将γ称之为增厚倍数.(3)本文的一个重要任务是确定岩石圈

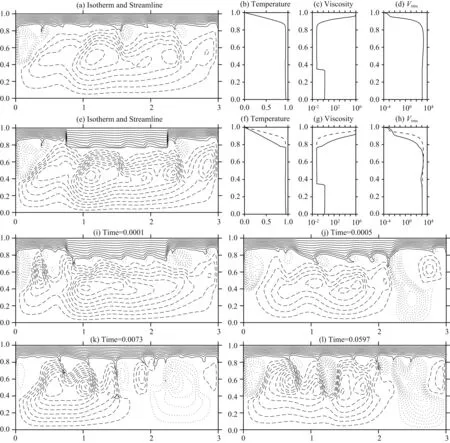
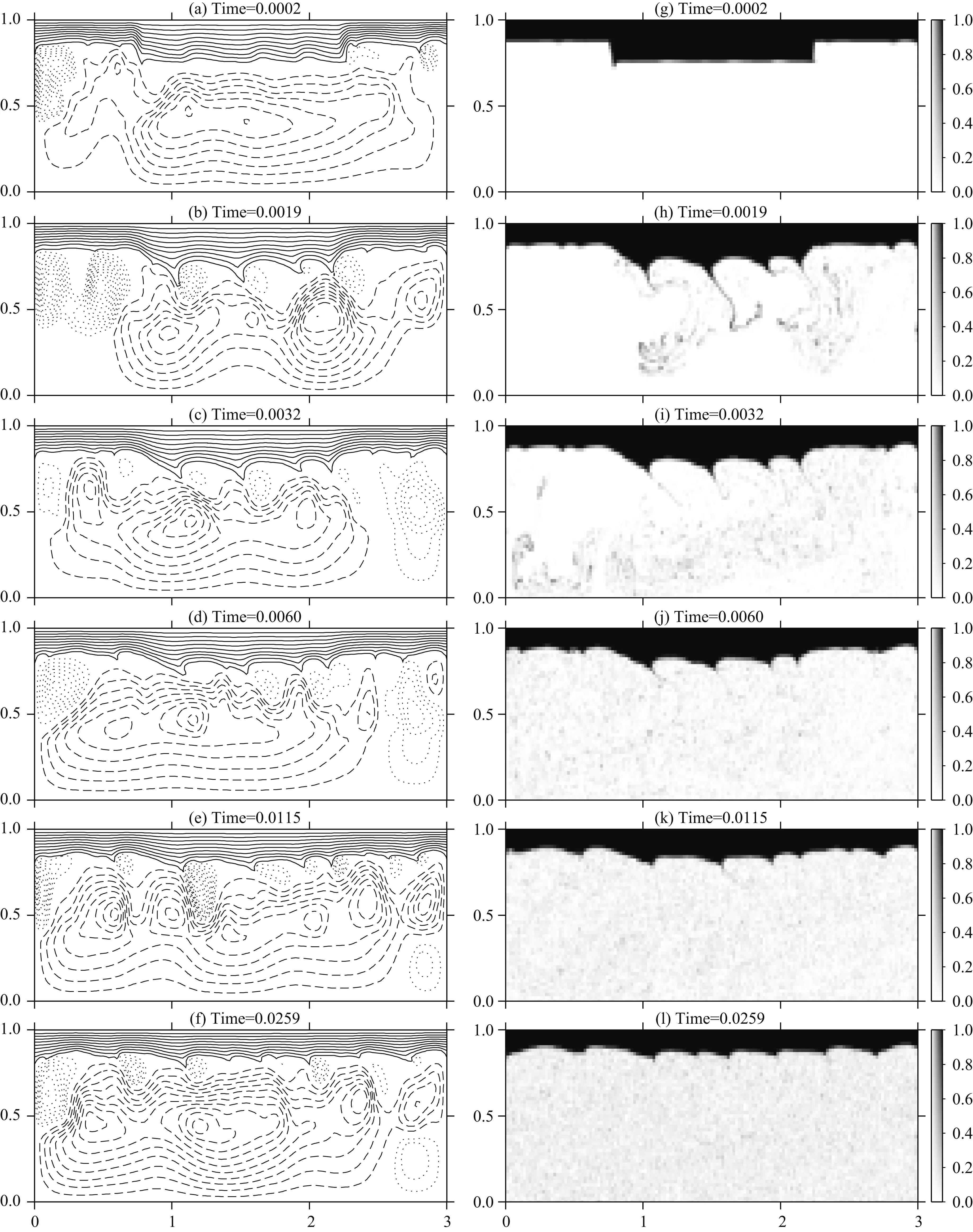
图1　参考模型在拟稳状态下的等温线和流线(a)以及横向平均温度(b)、黏性(c)和均方根速度Vrms(d).模型caseB3在初始状态下的等温线和流线(e)以及横向平均温度(f)、黏性(g)和Vrms(h)(f—h)中虚线是整个模型的横向平均值，实线是岩石圈加厚部分的横向平均值.(i—l)显示加厚岩石圈演化过程的温度场和流场.(a，e，i—l)中，实线代表等温线，相邻等温线间距为无量纲温度0.1，黑色点线表示流函数值小于零的流线，黑色虚线表示流函数值大于等于零的流线.Fig.1　Isotherm, streamline (a) and radial dependences of horizontal average temperature (b), viscosity (c) and Vrms (d) at the quasi stable state for the reference model. Isotherm, streamline (e) and radial dependences of horizontal average temperature (f), viscosity (g) and Vrms (h) at the initial state of the Model caseB3 The dashed line are displayed for the horizontal average value of the whole model and the solid line are displayed for the horizontal average of the thickened lithosphere in (f—h). (i—l) The temperature and flow field evolution of the thickened lithosphere. Solid line are displayed for isotherm, the spacing of adjacent isotherm is dimensionless temperature 0.1, black dotted line for positive streamline and black dashed line for negative streamline in (a，e，i—l).

对流减薄的时间.图1(e，i—l)分别给出了模型caseB3在岩石圈加厚后的温度场和流场的时间演化过程.从图中可以看到，经过一定时间的演化，增厚岩石圈厚度从(γ+1)Zq基本重新减薄到Zq.增厚岩石圈根移除时间的计算方法仍采用Morency等(2002)的方法，即计算每一时间步加厚岩石圈区域在深度Z=0.9Zq处的横向平均温度进而给出时间变化曲线(图2)，然后利用温度演化公式(Morency et al., 2002)：

(4)

对模型数据进行拟合，得到Ta、ta、Tst和A.其中ta是延迟时间，表示温度变化只有在此时间之后才符合(4)式；Ta相当于ta时间时，加厚岩石圈区域在Z=0.9Zq处的平均温度；Tst则相当于达到平衡时加厚岩石圈区域在Z=0.9Zq处的平均温度.岩石圈根移除时间定义为：

(5)

必须注意的是，当γ较小时，延迟时间ta近似为零(图2中的实线)，但当γ较大时，延迟时间ta就增大(图2中的虚点线).依此方法确定的模型岩石圈根移除时间计算结果见表2和表3.

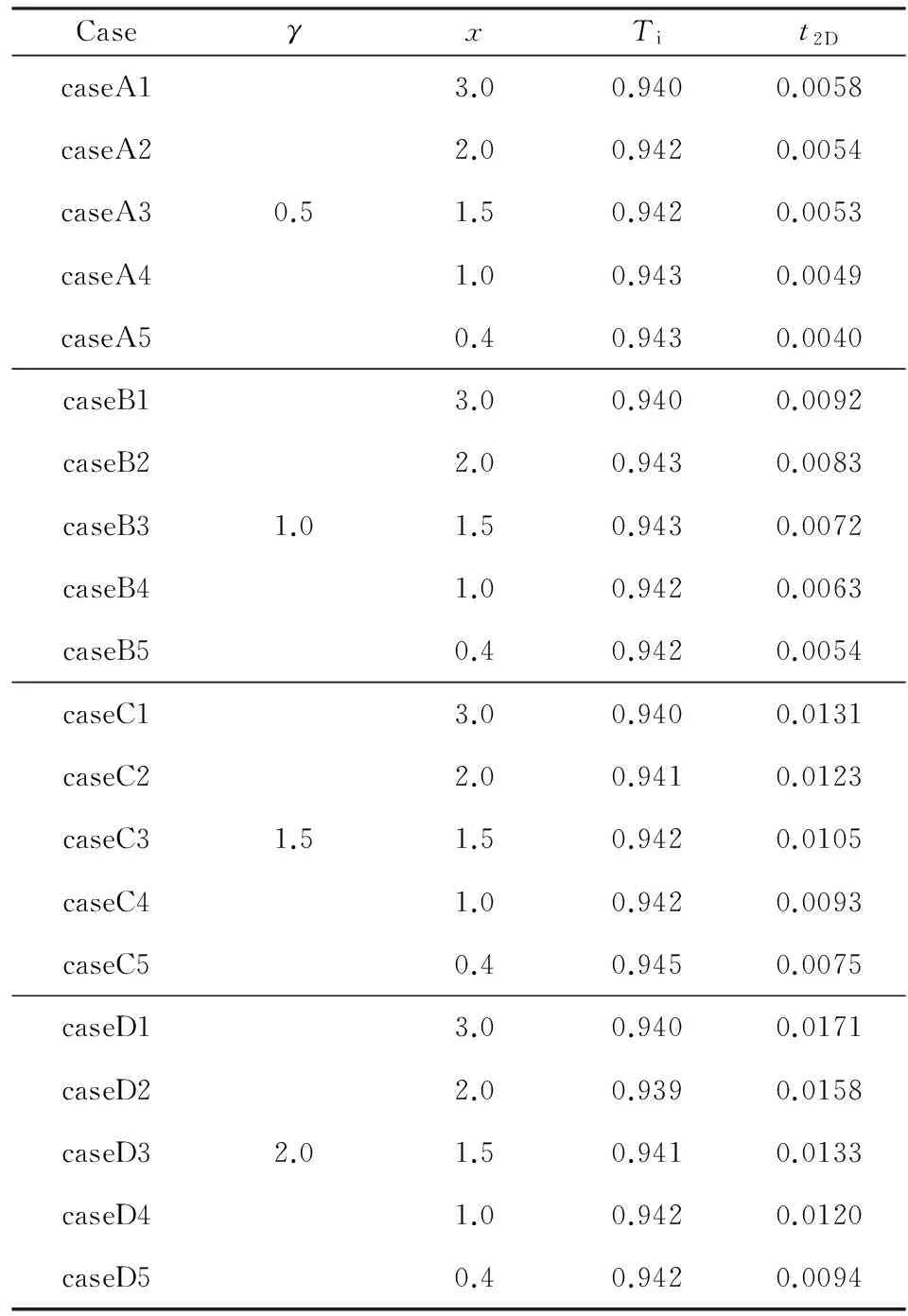
表2　模型参数和结果

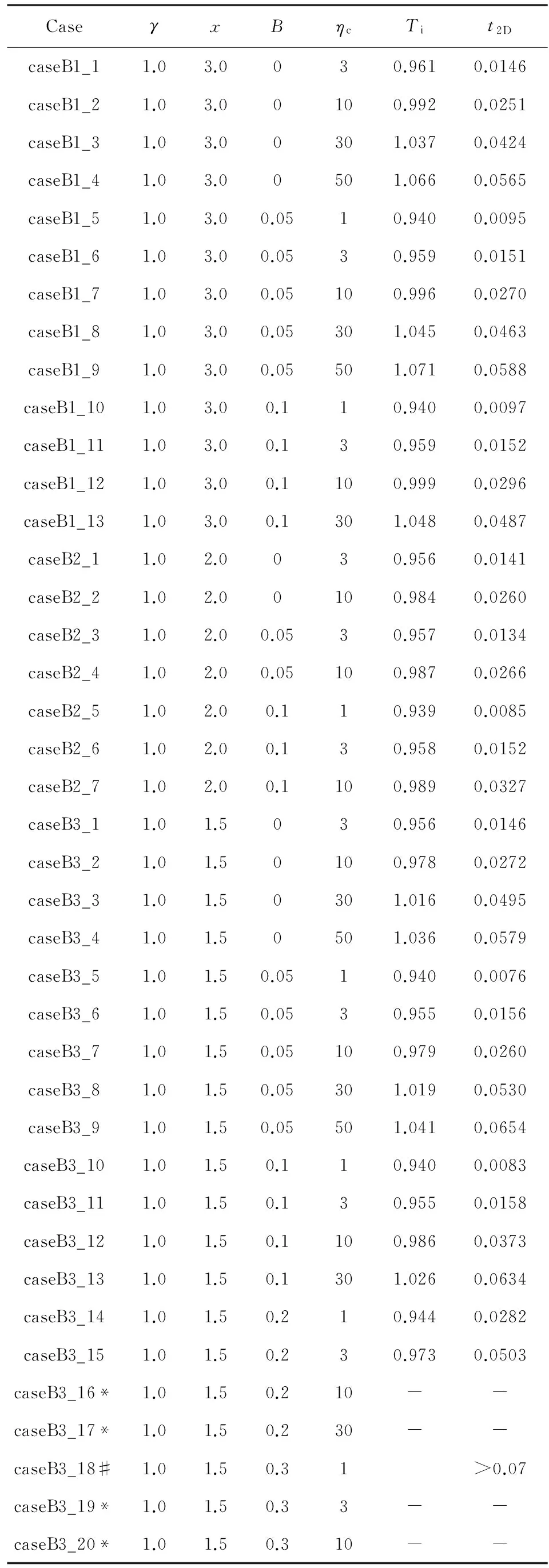
表3　模型参数和结果

续表3

注：*增厚的岩石圈根不能被完全移除，没有计算地幔内部温度Ti及移除时间t2D；#增厚的岩石圈根被移除掉，由于浮力数较大，0.9Zq处的横向平均温度变化复杂，不能使用上面的方法得到移除的具体时间，但能够大致得到移除时间在0.07以上.

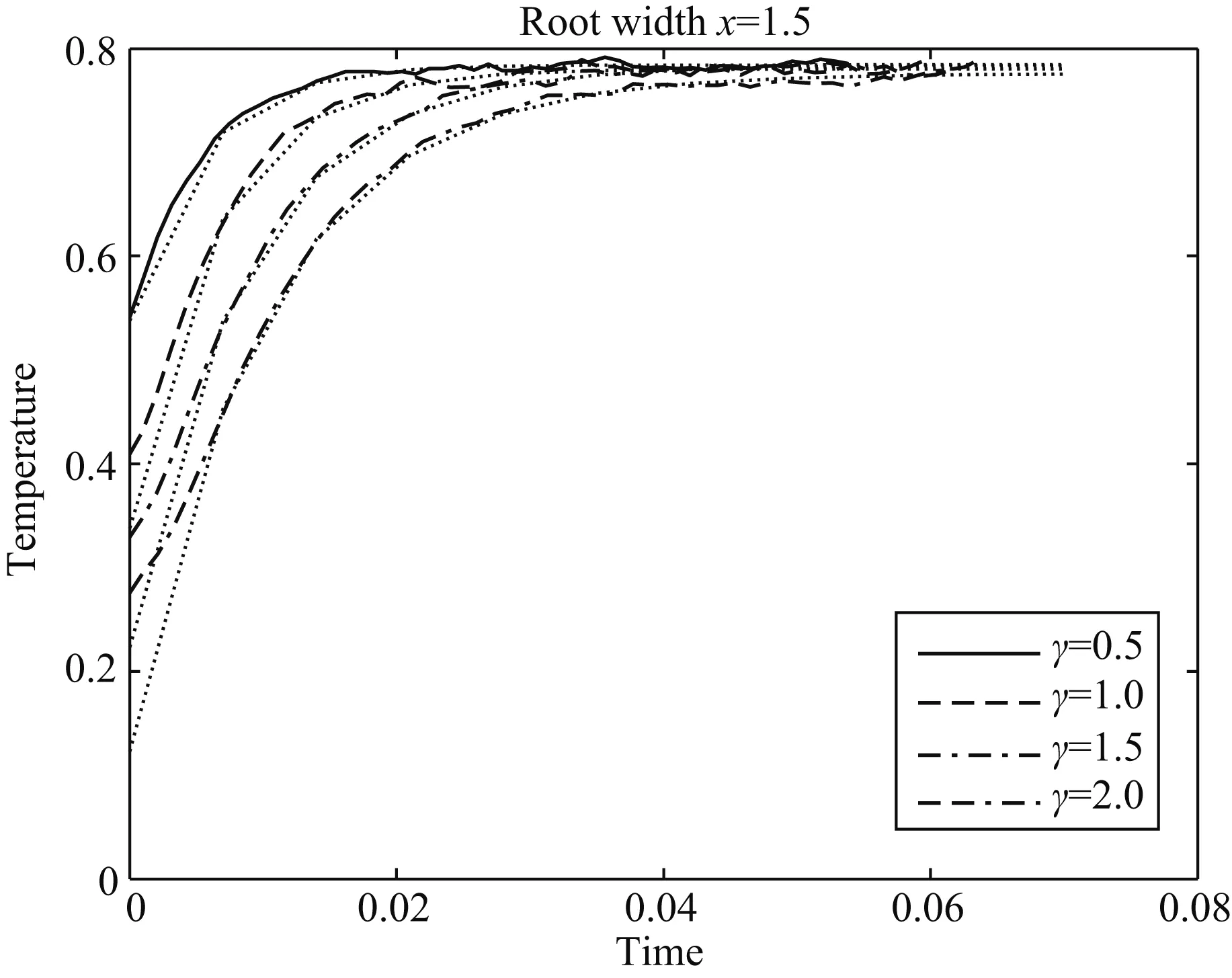
图2　深度Z=0.9Zq处的横向平均温度的时间演化曲线不同线型(点线除外)表示在不同的增厚倍数γ下的数值计算值，而通过对应线型的点线代表对应数值计算值的拟合曲线.Fig.2　Horizontal average temperature evolution with time at Z=0.9ZqThe line (except dotted line) in different linear are displayed for the numerical values of the different thickening factors γ and the dotted line corresponds to the line in different linear are displayed the fitting curves corresponds to the numerical values.

3数值结果

增厚岩石圈的对流减薄与岩石圈的物性参数密切相关(Huang et al., 2003;Morency et al., 2002).瑞利数和活化能等对岩石圈减薄过程具有重要影响(Huang et al., 2003;Morency et al., 2002)，但由于Morency等(2002)在其工作中详细分析和讨论了Ra(瑞利数)和E(活化能)对增厚岩石圈移除时间的影响，为能充分讨论克拉通岩石圈组分差异导致的密度和黏性的影响，本文将不再考虑Ra和E变化的影响，而是将其作为模型给定参数(参见表1).根据表1的模型参数，本文参考模型在处于拟稳状态时的热边界层厚度Zq=0.12.下面首先将给出B=0和ηc=1的一组模型的结果，该组模型忽略克拉通岩石圈固有的密度和黏性差异.然后通过改变B和ηc值研究克拉通岩石圈固有的密度和黏性差异的影响.即在讨论并总结一般岩石圈对流减薄规律的基础上，进一步讨论分析克拉通岩石圈对流减薄的规律.

3.1加厚岩石圈根的对流减薄

对一般加厚岩石圈，在本文模型中即假定B=0和ηc=1.该组模型与Morency等(2002)的模型基本一致.但应该注意，与Morency等(2002)模型不同的是，为和实际地球更加接近，本文考虑了660 km处的黏性跃变(Hager and Richards, 1989).表2给出了γ变化从0.5到2和x变化从0.4到3的共20个算例的结果.

图1(e，i—l)显示了模型caseB3的演化过程，该模型增厚岩石圈的宽度为1.5，增厚倍数为1.0.图1e是模型caseB3在初始时刻的等温线和流线.从图中可以看到，增厚岩石圈的减薄过程受到侧面和底部对流的影响(图1i和1j).在两侧以及底部对流的同时作用下，增厚的岩石圈逐步被移除、抹平(图1(i—k)).在0.0073时刻，增厚部分的岩石圈基本被移除(图1k).这与表2给出的、依据公式(4)和(5)计算得到的模型caseB3的移除时间0.0072基本一致.下面将详细分析增厚岩石圈移除时间与γ和x的关系.

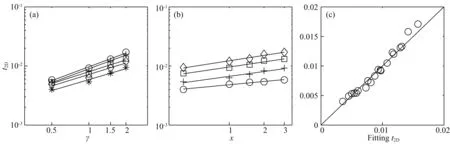
图3a给出了对流移除时间与增厚倍数γ的对数关系图.图中相同形状表示x相同的模型，连接相同形状的直线是通过线性拟合得到的相同x值下增厚岩石圈移除时间和增厚倍数的关系.从图中可以看到：对相同的x，对流移除时间与增厚倍数基本成幂函数关系，对流移除时间随增厚倍数增大而增大；对不同的x，拟合直线的斜率略有差异，但基本一致.计算结果显示：

(6)

图3b给出了对流移除时间与增厚宽度x的对数关系图.图中相同形状表示γ相同的模型.连接相同形状的直线是线性拟合得到的相同增厚倍数时，移除时间和增厚岩石圈宽度的关系.从图中可以看出，对流移除时间和增厚宽度也基本成幂函数关系，具体计算结果显示：

(7)

综合(6)式和(7)式的分析，我们得到对流移除时间与增厚倍数γ和增厚宽度x之间的量化关系：

(8)

图3c给出了根据(8)式计算的数值和表2中给出的模型结果的比较.从图中可以看到，式(8)可以很好地表示模型的计算结果，只是在移除时间很大和很小时略微存在差异.

根据(8)式可以方便地估算一个增厚岩石圈被对流减薄的时间.对于初始平衡厚度为120 km的岩石圈，将其厚度增加到300 km(即γ=1.5)，当增厚岩石圈宽度为300 km(x=0.3)时，增厚岩石圈根被移除的时间为225 Ma；而当加厚岩石圈宽度为1500 km(x=1.5)时，则其增厚岩石圈根的移除时间是342 Ma；而对于更大的加厚岩石圈宽度，如10000 km(x=10.0)，其根的移除时间是559 Ma.

尽管本文模型的黏性结构与Morency等(2002)的模型略有差别，但两者的结果仍具有一致性.Morency等(2002)通过数值计算和理论分析认为，加厚岩石圈的减薄包括侧面和底部的侵蚀影响，当加厚岩石圈宽度很小时，以侧面侵蚀为主；而当加厚岩石圈宽度很大时，以底部侵蚀为主.忽略次要影响的前提下，他们给出的无量纲关系式为：

当x

(10)

式中，x0是反映底部和侧面侵蚀作用的特征宽度，

(11)

式(9)—(11)中的变量与本文一致，其中V是无量纲的活化体积(无量纲参数为[V]=(RΔT)/(ρ0gD))，ΔTe是Morency等(2002)引进的流变温度(Davaille and Jaupart, 1994;Grasset and Parmentier, 1998;Solomatov and Moresi, 2000)，即

(12)

式中

(13)

如前面提到的，本文采用在深度大于660 km的下地幔黏性增加30倍来表示黏性随深度的变化，

图3　增厚岩石圈对流移除时间与增厚倍数γ(a)和宽度x(b)的关系；(c) 模型计算结果和拟合结果的比较Fig.3　Convective removal duration of the thickened lithosphere scale with the thickening factor γ (a) and width x (b)；(c) Comparison of the model results and the fitting results

而Morency等(2002)采用活化体积V*来表示黏性随深度的变化.要达到岩石圈下覆软流圈的黏性与下地幔的平均黏性相差约30倍，V*的取值大约应为0.75 cm3·mol-1，相应的无量纲的活化体积V=2.1621.根据表1及表2的数据，通过式(12)和(13)计算得到ΔTe=0.183.将此V及ΔTe值和本文模型的其他参数值代入(9)—(11)式，并取γ=1.5可计算得到无量纲的时间：

(14)

根据前面给出的时间和长度的量纲，式(14)量纲化，即为：

(15)

式中x*以km计.这意味着，对于初始平衡厚度为120 km的岩石圈，将其厚度增加到300 km(即γ=1.5)，当增厚岩石圈宽度为300 km时，其增厚岩石圈根被移除的时间为121 Ma；而当加厚岩石圈宽度为1500 km，则其根的移除时间是428 Ma.而对于更大的加厚岩石圈宽度，如10000 km，根据(15)式，其根的移除时间仍为428 Ma.

从上面的结果中可以看到，Morency等(2002)的结果与本文模型结果存在一定差异.这主要是由于Morency等(2002)在分析数据时的理论模型过于简单所导致的.如图1所示，增厚岩石圈根的移除是侧面和底部对流侵蚀同时作用的结果，但在Morency等(2002)的模型中，以特征宽度为界限，宽度小时忽略了底部的作用，而宽度大时又忽略了侧面的作用，所以他们的结果显示在宽度小时，移除时间与宽度成正比，而宽度较大时，移除时间与宽度无关.

3.2克拉通岩石圈根的对流减薄

本文关注的焦点是克拉通岩石圈根的对流减薄，这就涉及到克拉通岩石圈的密度和黏性参数的变化.因此，研究克拉通岩石圈根的对流减薄，即使不考虑Ra和E的影响，模型至少也包含有与克拉通岩石圈根的大小(γ,x)和化学组分导致的密度与黏性变化(B,ηc)有关的四个参量.前面已经研究了不考虑化学组分导致的密度与黏性变化情况下的增厚岩石圈根在热对流下的对流减薄问题，并得到了对流减薄时间和增厚的宽度以及厚度的量化关系.这里将在此基础上，通过改变B和ηc来模拟化学组分变化导致的克拉通岩石圈的密度和黏性变化，以讨论它们对克拉通岩石圈根的对流减薄的影响.表3给出了这组模型的计算结果.

比较表2和表3中移除时间的大小，我们发现在模型中增加克拉通岩石圈的密度和黏性变化后，增厚岩石圈根更难以被移除.但是，即使考虑克拉通岩石圈的密度和黏性的影响，当B和ηc较小时，岩石圈根的移除过程和3.1节模型所示的普通岩石圈根移除过程基本类似(如图4).岩石圈根的移除仍然是侧面和底部对流减薄共同作用的后果.图4显示了模型caseB3_7的温度、流场和克拉通岩石圈组分随时间演化的过程.

从图4可以看到模型温度场的演化和普通增厚岩石圈模型的(图1(e，i—l))演化相似，底部和侧面的对流侵蚀着岩石圈根，使其慢慢变薄，直至重新达到稳定.从组分场(图4(g—l))也可以看到，克拉通岩石圈组分被侧面和底部的对流带到了下部地幔并混入其中，增厚的克拉通岩石圈根逐渐被移除.表3显示caseB3_7的移除时间为0.0266，从图4中也可以看到，图4f和图4l对应的时间为0.0259，此时加厚的克拉通岩石圈根几乎被完全移除.

但当B或ηc较大时，移除时间将显著增长(表3).图5显示的是caseB3_14、caseB3_15、caseB3_16、caseB3_20和caseB3_23的组分时间演化图.该组模型的克拉通岩石圈根大小(γ=1.0,x=1.5)相同，克拉通组分变化导致的黏性变化ηc以及浮力数B的数值如图所示.从图5中可以明显看到，当B=0.2时，随着ηc的增大，增厚的岩石圈根的移除时间不断加长(图5中的第1,2,3行)，这也清楚地显示在岩石圈内温度场的演化上(图6).图6给出模型caseB3_14-17、caseB3_20和caseB3_23在深度Z=0.9Zq处的横向平均温度演化曲线.一般来说，该处的温度演化基本满足(4)式的指数规律(图2).图6中显示，在B=0.2且黏性比较小时(caseB3_14和caseB3_15)，平均温度曲线基本满足(4)式.拟合得到的增厚的岩石圈根移除时间分别为0.0282(894 Ma)和0.0503(1.60 Ga)(表3).但当黏性比较大时，在0.1的时间内，Z=0.9Zq处的横向平均温度一直处于上升阶段(图6中caseB3_16，ηc=10).这表明，在0.1的时间内克拉通岩石圈并没有被充分移除，这也反映在图5的组分场上(图5中的第3行).

图5还显示，当B或ηc足够大时(如ηc=10；B=0.3和0.4)，克拉通岩石圈的对流减薄过程与前述过程表现的非常不一样(图5中的第4,5行).图5显示，此时很少克拉通岩石圈组分被带入其下的地幔中，克拉通岩石圈组分在漫长的演化过程中，向两边扩散，这也会使得克拉通岩石圈得到部分减薄(图5中的第4,5行)，但这一过程非常漫长.从模型caseB3_20和caseB3_23在深度Z=0.9Zq处的横向平均温度演化曲线(图6中的较粗的实线和虚线)上看，平均温度在0.1时间内仍处于上升阶段.很显然，如果平均温度一直处于上升，就无法利用(4)式进行拟合，从而无法确定对流减薄时间.无量纲0.1的时间大约相当于3.17 Ga，这个时间非常长，如果模型在这么长时间内无法计算对流移除时间，我们就不将这类模型纳入后面的统计分析中.

图4　caseB3_7在不同时刻的(a—f)等温线及流线和(g—l)组分场演化(a—f)中实线代表等温线，相邻等温线间距为无量纲温度0.1.黑色点线表示流线为负值，黑色虚线表示流线为正值.Fig.4　The isotherm, streamline (a—f) and composition (g—l) evolution of the model caseB3_7, displayed at different time Solid line for isotherm, the spacing of adjacent isotherm is dimensionless temperature 0.1.Black dotted line for positive streamline and black dashed line for negative streamline in (a—f).

图5　不同组分黏性比以及浮力数下，增厚的克拉通岩石圈根的组分场演化.增厚克拉通岩石圈根的增厚倍数γ=1.0，增厚宽度x=1.5Fig.5　The composition of the thickening cratonic lithosphere, after stretching factor γ=1.0, width x=1.5, displayed at different viscosity ratio and buoyance number

图6　模型caseB3_14-17、caseB3_20和caseB3_23在深度Z=0.9Zq处的横向平均温度演化曲线实线、虚线、点划线、点线以及较粗的实线、虚线分别表示caseB3_14—17、caseB3_20和caseB3_23.Fig.6　Horizontal average temperature evolution with time at Z=0.9ZqSolid，dashed，dot-dashed，dotted line and the thicker solid，dashed line are displayed for caseB3_14—17，caseB3_20和caseB3_23.

(16)

(17)

其中，ΔTe是通过式(12)和(13)计算得到的，表3中的Ti略有变化，因此热化学对流模型的ΔTe也会变化.下面将仿照3.1节模型数据的分析方法对表3中数据进行分析.在我们的热化学对流模型中，除了增厚倍数γ和增厚区域宽度x外，还包括组分浮力数B和组分变化导致的黏性变化ηc.将组分浮力数B按照(17)式转化为Δρtc，则模型的四个参数为γ、x、ηc和Δρtc.参考3.1节的分析结果，假定：

(18)

下面将根据表3的结果确定(18)式中的幂指数.

图7a给出的是增厚区域宽度一定条件(x=1.0)下对流移除时间随着岩石圈增厚倍数γ的对数关系图，其中相同形状表示相同的组分黏性比ηc(圆圈表示ηc=1，方形表示ηc=3，菱形表示ηc=10)，而相同的线型则代表着相同的浮力数B(实线表示B=0，点划线表示B=0.05，虚线表示B=0.1)，通过相同形状的线条是其线性拟合.从图中能够看到：总体的趋势是对流移除时间随着增厚倍数的增大而增大，这和热对流的结果一致.同时，还可以看到，图7a中实线相连的菱形(caseB4_2、caseC4_2和caseD4_2)，点划线相连的菱形(caseB4_4、caseC4_5和caseD4_5)以及虚线相连的菱形(caseB4_7、caseC4_8和caseD4_8)对应的三条拟合直线几乎平行，其斜率相差不大，平均值约为0.33.实线相连的方形(caseB4_1,caseC4_1和caseD4_1)，点划线相连的方形(caseB4_3,caseC4_4和caseD4_4)以及虚线相连的方形(caseB4_6,caseC4_7和caseD4_7)对应的三条拟合直线也几乎平行，其斜率相差不大，平均值约为0.56.实线相连的圆圈(caseA4、caseB4、caseC4和caseD4)以及虚线相连的圆圈(caseB4_5、caseC4_6和caseD4_6)对应的两条拟合直线几乎平行，其斜率相差不大，平均值约为0.76.这说明对相同的ηc，对流移除时间随着增厚倍数的增大而增大，对流移除时间与增厚倍数基本成幂函数关系，B的影响不大(图7a中的相同形状的实线、虚线和点划线的斜率大致相同)；但对流移除时间与增厚倍数的关系的幂指数随着ηc的增大而减小(图7a中圆圈、方形和菱形对应的斜率，即θ，具体值见表4)，这说明对流移除时间与增厚倍数的关系与ηc相关.根据表4的结果，可以得到对流移除时间与增厚倍数的关系的幂指数θ与黏性变化ηc的关系(图7b).

图7　(a)对流移除时间和岩石圈根增厚倍数γ的量化关系；(b)量化关系参数θ随着组分黏性比ηc的变化关系；(c)去除了增厚倍数γ的影响后，对流移除时间随着组分黏性比ηc的量化关系；(d)去除了增厚倍数γ和组分黏性比ηc的影响后，对流移除时间随着Δρtc的量化关系；(e)去除增厚倍数γ，组分黏性比ηc以及Δρtc的影响后，对流移除时间随着增厚宽度x的量化关系；(f) 模型计算结果和拟合结果的比较Fig.7　(a) Convective removal duration scale with the lithospheric root thickening factor γ; (b) Scaling law parameters θ varies with the composition viscosity ratio ηc; (c) Convective removal duration scale with the composition viscosity ratio ηc without the effect of the lithospheric root thickening factor γ; (d) Convective removal duration scale with the Δρtc without the effect of the lithospheric root thickening factor γ and the composition viscosity ratio ηc; (e) Convective removal duration scale with the width x without the effect of the lithospheric root thickening factor γ, the composition viscosity ratio ηc and the Δρtc; (f) Comparison of the model results and the fitting results

表4　γ的量化关系参数

(19)

即

(20)

由图7a我们知道增厚倍数γ对于对流移除时间的影响很大，且当岩石圈的组分黏性比ηc不同时，影响的幅度也不同，所以在下面的分析数据中，我们都将增厚倍数对移除时间的影响利用(20)式去除后再来研究.去除增厚倍数的影响后，我们发现岩石圈的组分黏性比对移除时间的影响占主导地位(图7c—7e).图7c给出的是去除了增厚倍数γ的影响后，对流移除时间随着组分黏性比ηc的对数关系图，图中的圆圈包含表3中所有的B≤0.1的模型和表2中的caseB1、caseB2、caseB3、caseB4、caseC4和caseD4.图7c中包含18组数据.每组增厚倍数、增厚区域的宽度以及等效密度变化都相同.从图7c可以看到增厚倍数、增厚区域的宽度以及等效密度变化的影响几乎难以区分.因此在获取对流移除时间和ηc的幂指数时，我们采取将所有相同的ηc的模型的对流移除时间求平均，然后进行拟合，据此得到α=0.52，即

(21)

和3.1节一样，在讨论对流移除时间与等效密度变化Δρtc的关系时，也先将对流移除时间中包含的γ和ηc影响先行去除.图7d给出了去除了增厚倍数γ以及组分黏性比ηc影响后，对流移除时间随着等效密度变化Δρtc的变化规律，图中的圆圈同样包含了表3中所有的B≤0.1的模型和表2中的caseB1、caseB2、caseB3、caseB4、caseC4和caseD4.如图7d所示，随着热边界层总的等效密度变化的增大(浮力数的减小)，整体上的变化趋势是相同的，都表现出了对流移除时间在减小，这里采用对所有数据点进行线性拟合的方法确定(18)式中的β.拟合结果给出β=-0.21，故

(22)

最后，在得到(20)—(22)式的基础上，通过将对流移除时间进行归算，即扣除增厚倍数γ、组分黏性比ηc以及等效密度变化Δρtc的影响后来研究它和增厚宽度x的关系，如图7e所示.图7e给出的是去除了增厚倍数γ、组分黏性比ηc以及等效密度变化Δρtc的影响后，对流移除时间随着增厚区域宽度x的变化规律，图中的圆圈同样包含了表3中所有的γ=1.0且B≤0.1的模型和表2中的caseB1、caseB2、caseB3和caseB4.从图7e中可以看到：利用(20)—(22)式归算后，对固定的x，对流移除时间基本一致.因此，在获取(18)式的μ值时，我们再一次采用将相同x时的数据取平均的方法.根据平均值数据拟合得到μ=0.04，即

(23)

μ值很小，说明了增厚宽度x对减薄时间的影响很小，这与一般岩石圈对流减薄关系(8)式不同.这可能主要是由于在此种情况下，侧面对流侵蚀的影响显著减小.综合(20)—(23)式的分析，最后得到：

(24)

图7f给出了根据(24)式计算的移除时间和数值模型计算得到的移除时间之间的比较，从图7f中可以看到，(24)式可以很好地估算模型的计算结果.

式(24)可用来估算克拉通岩石圈被对流减薄的时间.采用3.1节相同的假定，即假定300 km(即γ=1.5)厚的克拉通岩石圈，在对流的作用下减薄到初始平衡厚度120 km.若克拉通岩石圈的密度比周围地幔的密度低0.4%(即B=0.1或Δρtc=0.082)且组分黏性比ηc=10，在克拉通岩石圈宽度为300 km(x=0.3)时，其对流减薄时间大约为1.11 Ga；在克拉通岩石圈宽度为1500 km(x=1.5)时，其对流减薄时间增加到大约1.18 Ga.对比3.1节结果可以看到，0.4%的组分密度变化和10倍的组分黏性变化，使得岩石圈的移除时间从225～342 Ma增加到1.11～1.18 Ga.这显示，克拉通岩石圈组分变化对移除时间具有重要影响.

保持其他参数不变，仅改变克拉通岩石圈组分浮力或黏性比，可以估算组分浮力或黏性比的影响.如仍假定300 km厚(即γ=1.5)、1500 km宽(x=1.5)、组分黏性比ηc=10，但若克拉通岩石圈的密度只比周围地幔的密度低0.2%(即B=0.05或Δρtc=0.132)，对流减薄时间略微减小为1.07 Ga.这说明组分密度的变化影响不大.但如仍假定300 km厚(即γ=1.5)、1500 km宽(x=1.5)、克拉通岩石圈的密度比周围地幔的密度低0.4%(即B=0.1或Δρtc=0.082)，而组分黏性比ηc=1，则依据(24)式，对流减薄时间约为426 Ma.这说明组分黏性的变化具有很大影响.

同样也可估算岩石圈厚度变化的影响.如假定240 km(即γ=1.0)厚的克拉通岩石圈，在对流的作用下减薄到初始平衡厚度120 km，根据(24)式，在克拉通岩石圈宽度为1500 km(x=1.5)和克拉通岩石圈的密度比周围地幔的密度低0.4%(即B=0.1或Δρtc=0.082)时，如组分黏性比ηc=10，克拉通岩石圈对流减薄时间大约是1.03 Ga.这显示，克拉通岩石圈的厚度也具有一定影响.

早期的研究显示，克拉通岩石圈根仅仅只有化学浮力并不能保持长期稳定，其根的强度(即克拉通岩石圈根的黏性，本文指组分黏性比ηc)是其保持长期稳定的关键因素(Lenardic and Moresi, 1999).最近，Wang等(2014)在研究克拉通的稳定性时，也指出在组分黏性比ηc=3时，具有浮力的克拉通岩石圈根就能在对流的地幔中保持长达亿年不受侵蚀；而当组分黏性比ηc增大到10，即使克拉通岩石圈具有的浮力更小抑或没有本身固有的浮力，都能在地幔中长期的稳定下来.这些都与式(24)的结果相一致.

根据目前的研究结果，华北克拉通岩石圈减薄发生在晚中生代，在早白垩世(120—130 Ma)达到高潮(吴福元等, 2008)，并且岩石圈的厚度从200多公里减薄到80～120 km左右，说明华北克拉通的减薄持续时间约为140 Ma.为能应用(24)式，这里假定华北克拉通从约200 km(即γ=0.67)厚经过对流减薄后减薄到120 km，空间尺度为1500 km(即x=1.5).如果根据一般克拉通都具有高黏性、低密度的特点，假定华北克拉通岩石圈的组分黏性比ηc=10(华北克拉通岩石圈的黏性是周围地幔黏性的10倍)，密度比周围地幔的密度低0.4%(即B=0.1或Δρtc=0.082)，那么根据(24)式，对流减薄时间约897 Ma.这个时间明显比140 Ma长.华北克拉通要在140 Ma得到减薄，必须发生交代置换或水化等作用使得密度或黏性产生变化.若仅发生密度变化，如交代作用使得克拉通岩石圈密度和周围地幔的密度相同(即B=0或Δρtc=0.182)，则对流减薄时间约为760 Ma；即使外推到克拉通岩石圈的密度比周围地幔高0.4%(即B=-0.1或Δρtc=0.282)，对流减薄时间也需约692 Ma.这说明如果化学交代等作用仅使克拉通岩石圈密度增大，就不足于在约140 Ma的时间内使得华北克拉通岩石圈的厚度减薄到120 km.但若考虑交代、熔融或水化等作用可以减小克拉通岩石圈的组分黏性比时，华北克拉通就可以在200 Ma内得到减薄.根据(24)式，即使假定华北克拉通岩石圈的密度仍比周围地幔的密度低0.4%，当组分黏性比减小到ηc=3时，对流减薄时间减小到约446 Ma；当组分黏性比减小到ηc=1，对流减薄时间减小到约227 Ma；如果组分黏性比降到ηc=0.5，那么克拉通岩石圈对流减薄时间就只需145 Ma.这与目前研究得到的华北克拉通可能由于太平洋的俯冲，经过脱水作用，华北克拉通岩石圈经历了强烈的水化，而大大降低了岩石圈的强度的结果一致(Xia et al., 2013;朱日祥等, 2012).

4结论

本文采用二维有限元数值模拟的方法，通过增厚(γ)一定宽度(x)内的拟稳状态下的模型边界层厚度来模拟加厚的岩石圈，然后考虑由化学组分引起的岩石圈的密度(B或Δρtc)和黏性变化(ηc)，定量研究了增厚的克拉通岩石圈在对流地幔中的移除时间，结果显示：

(1) 当B=0和ηc=1，即忽略克拉通岩石圈固有的密度和黏性差异时，加厚岩石圈的移除时间基本上是随着增厚岩石圈的宽度(x)增大而增大，同时也随着增厚岩石圈的厚度(γ)增大而增大，并且通过计算分析，得到移除时间和增厚岩石圈的宽度以及厚度的量化关系t2D=0.0073γ0.70x0.26.这显示，将一个初始厚度为120 km的岩石圈增厚到300 km，根据增厚的宽度(300 km或1500 km)的不同，其岩石圈根的对流移除时间在225 Ma或342 Ma不等.

(3) 对华北克拉通，如果其200 km厚的岩石圈是在140 Ma减薄到120 km厚，那么需要交代、熔融或水化作用减小其黏性.

致谢作者感谢李曙光老师以及Shijie Zhong教授对本研究提出的宝贵建议.

References

Boyd F R, Gurney J J, Richardson S H. 1985. Evidence for a 150～200 km thick Archaean lithosphere from diamond inclusion thermobarometry.Nature, 315(6018): 387-389.

Buck W R, Toksöz M N. 1983. Thermal effects of continental collisions: thickening a variable viscosity lithosphere.Tectonophysics, 100(1-3): 53-69.Carlson R W, Irving A J, Schulze D J, et al. 2004. Timing of Precambrian melt depletion and Phanerozoic refertilization events in the lithospheric mantle of the Wyoming craton and adjacent Central Plains Orogen.Lithos, 77(1-4): 453-472.

Carlson R W, Pearson D G, James D E. 2005. Physical, chemical, and chronological characteristics of continental mantle.Rev.Geophys., 43(1), doi: 10.1029/2004RG000156.

Davaille A, Jaupart C. 1994. Onset of thermal convection in fluids with temperature-dependent viscosity: application to the oceanic mantle.JournalofGeophysicalResearch, 99(B10): 19853-19866.

Davies G F. 1994. Thermomechanical erosion of the lithosphere by mantle plumes.JournalofGeophysicalResearch, 99(B8): 15709-15722.

Deng J F, Su S G, Zhao H L, et al. 2003. Deep processes of Mesozoic Yanshanian lithosphere thinning in North China.EarthScienceFrontiers(in Chinese), 10(3): 41-50.

Duggen S, Hoernle K, Van Den Bogaard P, et al. 2003. Deep roots of the Messinian salinity crisis.Nature, 422(6932): 602-606.

Fan W M, Menzies M A. 1992. Destruction of aged lower lithosphere and accretion of asthenosphere mantle beneath eastern China.GeotectonicaetMetallogenia(in Chinese), 16: 171-180.

Gao S, Rudnick R L, Carlson R W, et al. 2002. Re-Os evidence for replacement of ancient mantle lithosphere beneath the North China craton.EarthandPlanetaryScienceLetters, 198(3-4): 307-322.

Grasset O, Parmentier E M. 1998. Thermal convection in a volumetrically heated, infinite Prandtl number fluid with strongly temperature-dependent viscosity: Implications for planetary thermal evolution.JournalofGeophysicalResearch, 103(B8): 18171-18181.Griffin W L, Andi Z, O′reilly S Y, et al. 1998. Phanerozoic evolution of the lithosphere beneath the Sino-Korean Craton.∥ Mantle Dynamics and Plate Interactions in East Asia.AmericanGeophysicalUnion, 27: 107-126. Hager B H, Richards M A. 1989. Long-wavelength variations in earth′s geoid-physical models and dynamical implications.Philos.Trans.Roy.Soc.A, 328(1599): 309-327.

Houseman G A, Mckenzie D P, Molnar P. 1981. Convective instability of a thickened boundary layer and its relevance for the thermal evolution of continental convergent belts.JournalofGeophysicalResearch, 86(B7): 6115-6132.

Huang J S, Zhong S J, Van Hunen J. 2003. Controls on sublithospheric small-scale convection.JournalofGeophysicalResearch, 108(B8), doi: 10.1029/2003JB002456.

King S D. 2005. Archean cratons and mantle dynamics.EarthandPlanetaryScienceLetters, 234(1-2): 1-14.

Lenardic A, Moresi L N. 1999. Some thoughts on the stability of cratonic lithosphere: Effects of buoyancy and viscosity.JournalofGeophysicalResearch, 104(B6): 12747-12758.

Lenardic A, Moresi L N, Muhlhaus H. 2003. Longevity and stability of cratonic lithosphere: Insights from numerical simulations of coupled mantle convection and continental tectonics.JournalofGeophysicalResearch, 108(B6), doi: 10.1029/2002JB001859.

Li J H, Niu X L, Kusky T, et al. 2004. Neoarchean plate tectonic evolution of North China and its correlation with global cratonic blocks.EarthScienceFrontiers(in Chinese), 11(3): 273-283.

Liu D Y, Nutman A P, Compston W, et al. 1992. Remnants of ≥3800 Ma crust in the Chinese Part of the Sino-Korean craton.Geology, 20(4): 339-342.

Lu F X, Han Z G, Zheng J P, et al. 1991. Characteristics of Paleozoic mantle-lithosphere in Fuxian, Liaoning Province.GeologicalScienceandTechnologyInformation(in Chinese), 10(S1): 2-20.

Marotta A M, Fernàndez M, Sabadini R. 1999. The onset of extension during lithospheric shortening: a two-dimensional thermomechanical model for lithospheric unrooting.Geophys.J.Int., 139(1): 98-114.

Menzies M A, Fan W M, Zhang M. 1993. Palaeozoic and Cenozoic lithoprobes and the loss of >120 km of Archaean lithosphere, Sino-Korean craton, China.GeologicalSociety,London,SpecialPublications, 76(1): 71-81.Morency C, Doin M P, Dumoulin C. 2002. Convective destabilization of a thickened continental lithosphere.EarthandPlanetaryScienceLetters, 202(2): 303-320. Moresi L N, Solomatov V S. 1995. Numerical investigation of 2D convection with extremely large viscosity variations.Phys.Fluids, 7(9): 2154-2162.

Olson P, Schubert G, Anderson C, et al. 1988. Plume formation and lithosphere erosion: A comparison of laboratory and numerical experiments.JournalofGeophysicalResearch, 93(B12): 15065-15084.

O′Neill C J, Lenardic A, Griffin W L, et al. 2008. Dynamics of cratons in an evolving mantle.Lithos, 102(1-2): 12-24.

Pearson D G, Snyder G A, Shirey S B, et al. 1995. Archean Re-Os age for Siberian eclogites and constraints on Archaean tectonics.Nature, 374(6524): 711-713.

Pearson D G. 1999. The age of continental roots.Lithos, 48(1-4): 171-194.

Qiao Y C, Guo Z Q, Shi Y L. 2012. Numerical simulation of a possible thinning mechanism of the North China Craton-Gravitational instability delamination induced by lower crust eclogite.ChineseJ.Geophys. (in Chinese), 55(12): 4249-4256, doi: 10.6038/j.issn.0001-5733.2012.12.036.

Qiao Y C, Guo Z Q, Shi Y L. 2013. Thermal convection thinning of the North China Craton: Numerical simulation.ScienceChina:EarthSciences, 56(5): 773-782.

Rudnick R L, Fountain D M. 1995. Nature and composition of the continental crust: a Lower crustal perspective.Rev.Geophys., 33(3): 267-309. Schott B, Schmeling H. 1998. Delamination and detachment of a lithospheric root.Tectonophysics, 296(3-4): 225-247.

Schubert G, Turcotte D L, Olson P. 2001. Mantle Convection in the Earth and Planets. Cambridge, UK: Cambridge University Press, 940.

Schurr B, Rietbrock A, Asch G, et al. 2006. Evidence for lithospheric detachment in the central Andes from local earthquake tomography.Tectonophysics, 415(1-4): 203-223.

Shao J A, Zhang L Q, Li D M. 2002. Three Proterozoic extensional events in North China Craton.ActaPetrologicaSinica(in Chinese), 18(2): 152-160.

Shapiro S S, Hager B H, Jordan T H. 1999. Stability and dynamics of the continental tectosphere.Lithos, 48(1-4): 115-133.

Solomatov V S, Moresi L N. 2000. Scaling of time-dependent stagnant lid convection: Application to small-scale convection on Earth and other terrestrial planets.JournalofGeophysicalResearch, 105(B9): 21795-21817.

Turcotte D L, Schubert G. 2002. Geodynamics. Cambridge: Cambridge University Press.

Wang H L, Van Hunen J, Pearson D G, et al. 2014. Craton stability and longevity: The roles of composition-dependent rheology and buoyancy.EarthandPlanetaryScienceLetters, 391: 224-233.

Wu F Y, Ge W C, Sun D Y, et al. 2003. Discussions on the lithospheric thinning in eastern China.EarthScienceFrontiers(in Chinese), 10(3): 51-60.

Wu F Y, Lin J Q, Wilde S A, et al. 2005. Nature and significance of the Early Cretaceous giant igneous event in eastern China.EarthandPlanetaryScienceLetters, 233(1-2): 103-119.

Wu F Y, Xu Y G, Gao S, et al. 2008. Lithospheric thinning and destruction of the North China Craton.ActaPetrologicaSinica(in Chinese), 24(6): 1145-1174.

Xia Q K, Liu J, Liu S C, et al. 2013. High water content in Mesozoic primitive basalts of the North China Craton and implications on the destruction of cratonic mantle lithosphere.EarthandPlanetaryScienceLetters, 361: 85-97.

Xu W L, Wang Q H, Wang D Y, et al. 2004. Processes and mechanism of Mesozoic lithospheric thinning in eastern North China Craton: evidence from Mesozoic igneous rocks and deep-seated xenoliths.EarthScienceFrontiers(in Chinese), 11(3): 309-313.

Xu Y G. 2001. Thermo-tectonic destruction of the Archaean lithospheric keel beneath the Sino-Korean Craton in China: Evidence, timing and mechanism.Phys.Chem.EarthA, 26(9-10): 747-757.

Yoshida M. 2012. Dynamic role of the rheological contrast between cratonic and oceanic lithospheres in the longevity of cratonic lithosphere: A three-dimensional numerical study.Tectonophysics, 532-535: 156-166. Yuen D A, Fleitout L. 1985. Thinning of the lithosphere by small-scale convective destabilization.Nature, 313(5998): 125-128.

Zhao G C, Wilde S A, Cawood P A, et al. 2001. Archean blocks and their boundaries in the North China Craton: lithological, geochemical, structural and P-T path constraints and tectonic evolution.PrecambrianRes., 107(1-2): 45-73.

Zhao L, Zheng T Y. 2007. Complex upper-mantle deformation beneath the North China Craton: implications for lithospheric thinning.Geophys.J.Int., 170(3): 1095-1099.

Zhao Y, Xu G, Zhang S Z, et al. 2004. Yanshanian movement and conversion of tectonic regimes in East Asia.EarthScienceFrontiers(in Chinese), 11(3): 319-328.

Zhong S J, Zuber M T, Moresi L, et al. 2000. Role of temperature-dependent viscosity and surface plates in spherical shell models of mantle convection.JournalofGeophysicalResearch, 105(B5): 11063-11082.

Zhu R X, Chen L, Wu F Y, et al. 2011. Timing, scale and mechanism of the destruction of the North China Craton.ScienceChina:EarthSciences, 54(6): 789-797.

Zhu R X, Xu Y G, Zhu G, et al. 2012. Destruction of the North China Craton.ScienceChina:EarthSciences, 55(10): 1565-1587.

附中文参考文献

邓晋福, 苏尚国, 赵海玲等. 2003. 华北地区燕山期岩石圈减薄的深部过程. 地学前缘, 10(3): 41-50.

范蔚茗, Menzies M A. 1992. 中国东部古老岩石圈下部的破坏和软流圈地幔的增生. 大地构造与成矿学, 16: 171-180.

李江海, 牛向龙, Kusky T等. 2004. 从全球对比探讨华北克拉通早期地质演化与板块构造过程. 地学前缘, 11(3): 273-283.

路凤香, 韩柱国, 郑建平等. 1991. 辽宁复县地区古生代岩石圈地幔特征. 地质科技情报, 10(S1): 2-20.

乔彦超, 郭子祺, 石耀霖. 2012. 数值模拟华北克拉通岩石圈减薄的一种可能机制——下地壳榴辉岩重力失稳引起的拆沉. 地球物理学报, 55(12): 4249-4256, doi: 10.6038/j.issn.0001-5733.2012.12.036.

乔彦超, 郭子祺, 石耀霖. 2013. 数值模拟华北克拉通岩石圈热对流侵蚀减薄机制. 中国科学: 地球科学, 43(4): 642-652.

邵济安, 张履桥, 李大明. 2002. 华北克拉通元古代的三次伸展事件. 岩石学报, 18(2): 152-160.

吴福元, 葛文春, 孙德有等. 2003. 中国东部岩石圈减薄研究中的几个问题. 地学前缘, 10(3): 51-60.

吴福元, 徐义刚, 高山等. 2008. 华北岩石圈减薄与克拉通破坏研究的主要学术争论. 岩石学报, 24(6): 1145-1174.

许文良, 王清海, 王冬艳等. 2004. 华北克拉通东部中生代岩石圈减薄的过程与机制: 中生代火成岩和深源捕虏体证据. 地学前缘, 11(3): 309-313.

赵越, 徐刚, 张拴宏等. 2004. 燕山运动与东亚构造体制的转变. 地学前缘, 11(3): 319-328.

朱日祥, 陈凌, 吴福元等. 2011. 华北克拉通破坏的时间、范围与机制. 中国科学: 地球科学, 41(5): 583-592.

朱日祥, 徐义刚, 朱光等. 2012. 华北克拉通破坏. 中国科学: 地球科学, 42(8): 1135-1159.

(本文编辑何燕)

Numerical simulation on convective thinning of the cratonic lithosphere

1LaboratoryofSeismologyandPhysicsofEarthInterior,SchoolofEarthandSpaceSciences,UniversityofScienceandTechnologyofChina,Hefei230026,China2MengchengNationalGeophysicalObservatory,Hefei230026,China

AbstractConvective removal on lithospheric root, especially on cratonic lithosphere root is studied via numerical simulations in 2D models. The control parameters in the models include the width, x, stretching factor, γ, viscosity ratio, ηc, and chemical buoyancy number, B, or effective density contrast, Δρtc. Numerical results show that mantle convection thins the thickened lithosphere, and (1) when B=0 and ηc=1, i.e., for general lithosphere, the root removal duration is scaled as 0.0073γ0.70x0.26, which means, for a 300 km thickness lithosphere with an initially equilibrium thickness of 120 km, and a root width of 300 km or 1500 km, it takes 225 Ma or 342 Ma to thin by sublithospheric convection to its equilibrium; (2) for small B and ηc, the process to thin cratonic lithosphere is similar to that to thin general lithosphere, but the root removal duration is increased significantly, and the root removal duration is scaled as With this scaling law, for a 300 km thickness lithosphere with an initially equilibrium thickness of 120 km, and a root width of 1500 km, the root removal duration is 1.18 Ga if ηc=10; and (3) for large B and ηc(B≥0.2 and ηc>10), the process to thin cratonic lithosphere is very different. Because of the influences of chemical buoyancy and viscosity, the cratonic lithosphere is spread to adjacent lithosphere instead of mixing with underneath mantle. In these cases, the root removal duration is very long (>3 Ga).

KeywordsCratonic lithosphere; Lithospheric thinning; Lithospheric root removal duration

基金项目国家自然科学基金项目(41474082,91014005)资助.

作者简介程华冬，男，1986年生，安徽省肥西县人，主要研究方向：地球动力学.E-mail:chengyd@mail.ustc.edu.cn *通讯作者黄金水，男，教授，主要研究方向：地球动力学.E-mail:jshhuang@ustc.edu.cn

doi:10.6038/cjg20160412 中图分类号P315

收稿日期2015-01-27，2016-03-04收修定稿