车辆监控中电子围栏的设计与实现
周喜平 姜斌
摘要:在车辆监控的地图上,绘制一种基于矩形、圆形、多边形的电子围栏,当车辆在区域内满足相应条件的时候,能够报警或者做一些其他联动处理。利用车辆GPS坐标结合电子围栏的地图信息,建立数学模型,设计算法,并通过编程实现车辆出区入区的判断。该设计通过实际应用,效果较好。
关键词:车辆监控;电子围栏;出区入区;GPS坐标
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2016)13-0107-03
Abstract: On the vehicle monitoring map, draw a rectangle, circle, polygon of the electronic fence, when the vehicle in the area to meet the appropriate conditions, can alarm or do some other linkage processing. By using the GPS coordinate of the vehicle and the map information of the electronic fence, the mathematical model is built, and the algorithm is designed. This software is implemented by programming. This software through the practical application, the effect is good.
key words: vehicle monitoring ;electronic fence;GPS coordinate
1 背景
基于地图的车辆监控系统中,电子围栏是一个非常实用的功能。所谓电子围栏,就是在地图上绘制一个图形区域,如果车辆进入或者离开该区域,监控系统会按照事先设定的条件,触发相关的处理程序。该区域可以是规则的矩形、圆形,也可以是不规则的图形,比如不规则的多边形。本设计针对矩形、圆形和不规则的多边形,进行讨论,提供一种解决方法,设计实现的算法,并通过Java编程实现应用程序。
2 设计与实现
一般的车辆监控系统中,车辆的GPS位置信息是通过安装在车上的GPS芯片完成GPS位置信息的感知,并通过通信网络接入到采集服务器中。采集服务器将采集到的位置信息进行持久化,以备数据分析和后期处理。本设计以关系数据库为例,假设位置信息是保存在关系数据库中的。另外,GPS芯片感知的位置信息中,经纬度是地球坐标系,在不同的地图上进行展示时,还要转换成对应地图支持的坐标系,否则会产生较大偏移。关于坐标系的转换,这里不再论述,这里假定地图是直接支持地球坐标系的。
GPSinfo表用以保存位置信息,其结构为GPSinfo(carid,lng,lat,addtime),carid为车辆标识,lng为经度信息,类型为浮点型,lat为纬度信息,类型为浮点型,addtime为采集的时间。一个代表性的数据是(7698,113.653655,35.045452, ‘2015/9/15 20:50:18‘)。
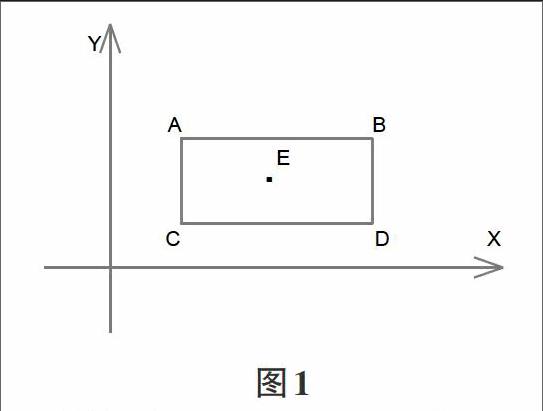
2.1 矩形区域处理
针对矩形区域处理,复杂度较低。设矩形ABCD的四个顶点分别为A,、B、C、D,坐标分别为A(x1,y1,)(x1,y1为A点经度纬度坐标,下同)、B(x 2,y2,)、C(x3,y3,)、D(x4,y4,),设点E(x5,y5)是采集到的车辆的坐标,那么判断E点在矩形区域的方法是:x5>x3 且 x5 2.2 圆形区域处理 对于圆形区域,我们假设地球是正圆的,同时假设圆心为B(Xb,Yb),A(Xa,Ya)为判断的点, Xb,Yb为B点经纬度,Xa,Ya为A点经纬度,A、B是地求表面的两个点,如图2中的a所示,已知A、B两点的经度后,我们可以计算CD的地表长度为: 其中,R可取值6378千米,PI可取值3.1416。考虑到查询的性能,我们可以在查询之前,对查找的记录做一些预筛选,找到圆的外切正方形的四个顶点,按照判断点在矩形区域的方法,找到矩形区域中的点,之后再判断是否在圆内,由于减少了记录数量,查询性能上有所提升。 2.3 多边形区域处理 如图3,判断点p在多边形内的方法是:用p点的水平坐标去和多边形相交,得到若干个交点,如果点p两侧的交点数量都是奇数个时,说明p点在多边形内,即铅垂线内点法[1]。使用这种方法,适合任意多边形,包括凸多边形和凹多边形,同时适用于有孔的多边形。下面给出这种算法的Java实现,其中polySides是多边形的顶点数量,polyX为顶点的x坐标数据,polyY为顶点的Y坐标数组。若方法pointInPolygon返回true则表名测试点t(x,y)在多边形内部。 boolean pointInPolygon() { int i,j=polySides-1 ; boolean oddNodes=false; for (i=0;i if(polyY[i] if(polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i]) oddNodes=!oddNodes; } } j=i; } return oddNodes; } 其实,在Java语言的开发环境中,提供了一种便捷的方法。类java.awt.geom.GeneralPath提供了根据直线、二次曲线和三次 (Bézier) 曲线构造的几何路径的方法,同时GeneralPath类继承类Path2D,通过Path2D类提供的方法contains(double x, double y) 来判断某个点是否在曲线或直线构成的边界内。一种可行的使用方法是: Point2D.Double first = polygon.get(0); p.moveTo(first.x, first.y); for (Point2D.Double d : polygon) p.lineTo(d.x, d.y); p.lineTo(first.x, first.y); p.closePath(); return p.contains(point); 其中p为构造的GeneralPath对象,polygon包含了多边形顶点的List对象,每个顶点被定义为Point2D.Double类型。point 则是要判断的点,其类型也为Point2D.Double。p.contains (point)返回true则表示点point包含在多边形polygon内。 在处理数据库中的数据时,可以先将多边形外切的矩形作为选区,选出满足矩形选区的点,之后可以在判断选出的点是否在多边形区域内,这样可以一定程度上改善数据库操作的性能。 3 结束语 以上处理方法,在实际应用中取得了较好的效果,图4、5、6分别展示了当车进入矩形、圆形、多边形区域后立即显示到地图上的效果。如果结合出区入区的其他条件,比如出入区时间、区域内车辆速度、出入区次数等其他条件,则能够设计和实现更加复杂的程序,以满足更多的应用场合。 参考文献: [1] 王润科, 张彦丽. 判断点与多边形位置关系的算法综述[J]. 甘肃联合大学学报, 2006,20(11): 32-35.

