RLC串联电路谐振频率测量方法的比较研究

周宦银 沈庭云 文其林 李丽蓉 谢艳辉 曹剑锋

防化学院 北京 102205



RLC串联电路谐振频率测量方法的比较研究

周宦银 沈庭云 文其林 李丽蓉 谢艳辉 曹剑锋

防化学院 北京 102205

摘 要：RLC串联电路的谐振频率一般采用最大电流或最大电压法进行测量，但是，该测量方法精度较低，尤其在电路品质因数较低的情况下，这种方法很难准确测出谐振频率值。本文根据谐振电路的特点，经过多年的教学实践，总结了多种实用的谐振频率测量方法，并对谐振频率的测量方法进行了比较研究。得出了不同的测量方法测量精度不同；电路参数不同，选用合理的测量方法，可大大提高测量精度的结论。

关键词：RLC串联电路；谐振频率；测量方法；精度；比较

RLC串联谐振电路是电工学中的典型的电路之一，能很好地加深学生对交流电路的理解，并在实际中得到了较为广泛的应用［1］。在测量电路的谐振频率时，一般都采用谐振时电路中电流最大，电阻两端电压最大的方法进行测量［2，3］。文献［4］提出了8种测量RLC串联电路谐振频率的方法，这些方法理论上都成立，但是实际测量时有些问题，存在的主要问题有：（1）用万用表测交流电压、电流不够准确，万用表一般只适用于测工频附近频率的交流电压、电流；（2）忽略电感等的自身电阻影响；（3）忽略了示波器的探笔负极共地的问题，采用此方法可能导致完全错误的结果甚至烧坏电路或仪器［5］；（4）文献没有对不同方法进行比较，测量方法不同测量精度不同，尤其是对电路参数不同时哪种方法精度高，何时适用何种方法没有进行分析研究。其他文献［6，7］也未就谐振频率的精确测量进行深入分析研究。

由于测量仪表采样等原因，无论在实物实验、还是仿真实验时都可以看到，交流电压的读数常有1%左右的波动，如：测量1 V左右的交流电压，读数往往在0.99 V～1.01V之间波动，难以准确测量。由于电阻上的交流电压测量不准确，对应的电源频率测量就不准确，某些时候测量误差可能很大。同时，由于RLC串联电路幅频特性曲线在谐振频率点时取最大值，此时特性曲线对频率的导数为零，在该频率点电阻电压变化随频率变化最不敏感，即频率较大变化时，电阻电压变化小，因此谐振频率难以准确测量，对品质因数低的电路，测量误差更大。用什么方法可提高谐振频率的测量精度呢？根据电路参数不同，选用不同的测量方法可以提高谐振频率的测量精度。下面通过理论分析和EWB仿真实验辅助分析的方法［8］，对RLC串联电路的谐振频率测量方法进行比较研究。

1 RLC串联电路谐振频率的测量方法比较

根据RLC串联电路的特性，可以利用谐振时电路的特点确定电路什么时候处于谐振状态，测出谐振频率［9］。

1.1 最大电流、电压法

该方法是最传统、使用最多的方法。由串联谐振电路的特点可知，电路发生谐振时，电容的容抗和电感的感抗抵消，电抗为零，电路总阻抗最小，电路呈电阻性，在电源幅度一定的情况下，电路中的电流最大，电阻两端的电压也最大。因此可以通过测量电阻两端电压最大的方法测量电路的谐振频率，测量原理图如图1所示。电路参数选用天煌教仪实验箱参数值，C=2 200 pF，L=30 mH，R=2.2 KΩ。

理论分析可知，电路的谐振频率：

电路的品质因数：

图1 利用最大电流、电压法测谐振

实验时电压读数值总是在约1%的范围内波动，如图1电路中，仿真时电压表读数出现大于1 V情况，不能准确地读到最大值。由于上述电路品质因数低，电路选频性能差，在谐振频率两侧的较大范围内，难以观测到电阻电压变化，此时很难准确地找到谐振频率点。

现假定电压测量误差为1%，理论分析可知，当f0=19.59 kHz时，电路谐振，UR=1 V；当电源频率为f1=18.785 kHz时，XC=3 851.1Ω，XL=3 540.9Ω，X=310.2 Ω，此时UR=0.99 V；当电源频率为f2=20.431 kHz时，XC=3 540.8 Ω，XL=3 851.1 Ω，X=310.3 Ω，此时UR=0.99 V。也就是说，当交流电源的频率f在18.785 kHz到20.431 kHz之间变化时，频率变化范围为1.65 kHz，UR的值在1 V的1%范围变化，在这样很宽的频率范围内，电阻电压变化随频率变化不明显，很难用交流毫伏表或示波器准确判断在什么频率时电阻两端电压最大，因此利用这种方法难于准确测出谐振频率点。

电路参数对RLC电路的谐振特性常常有影响［10］。若将电阻R值改为100Ω，其他参数不变，此时谐振频率不变，品质因数提高到37，同样以1%为界，当频率变化在19.553 kHz至19.628 kHz范围内时，电阻两端的电压值在最大电压的1%误差范围内，因此可更准确地找出谐振频率在19.553 kHz至19.628 kHz范围内，此时测量谐振频率点的精度可以提高。若考虑电感的电阻值，电路谐振时，电阻R两端电压也是最大，最大电流、电压法同样适用。

因此，用传统的测量电阻两端电压最大的方法测量谐振频率精度不高，尤其是当电路品质因数较低时，用最大电流、电压法测量谐振频率误差较大，不宜采用该方法进行测量。该方法一般适用于品质因数高的电路。

1.2 电容、电感总电压最小法

当电路发生串联谐振时，电阻两端电压最大，则电容、电感两端总电压ULC最小。利用测量电容、电感两端总电压最小的方法可以测出电路的谐振频率。电容、电感总电压最小法电路原理图如图2所示。

图2 利用电容、电感总电压最小法测谐振

由于电容、电感两端总电压ULC较小，因此可减小电压表量程来测量总电压，当总电压最小时，所对应的交流电源的频率即为谐振频率。

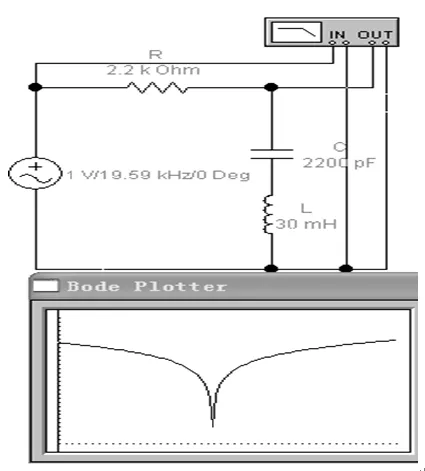
图3 电容电感总电压法电路的幅频特性

用EWB波特表对该方法进行辅助分析，电路图和幅频特性如图3所示，可以看出，在谐振频率附近，幅频特性曲线斜率大，电容电感总电压变化对频率变化非常敏感，即细微的频率变化，将引起电压幅度明显变化。因此该方法测量谐振频率非常准确。

考虑电感的电阻值时，电路谐振时，电阻R两端电压最大，电感和电阻两端电压同样是最小，因此，考虑电感的电阻值时，电容、电感总电压最小法同样适用。理论分析可知，电阻越大，电感电阻越小，测量精度越高。

因此，该方法测量精度高，非常适用于电阻R较大，电感电阻较小的电路的测量。

1.3 电阻电压与电源电压同相法

当电路发生串联谐振时，电路阻抗呈现纯电阻性，此时电流与电源电压同相，电阻两端电压与电源电压也同相。因此，可以用双踪示波器比较电源电压和电阻两端电压相位的方法来判断电路谐振，当两者同相时，电路谐振，此时对应的频率为谐振频率。电阻电压与电源电压相位比较法电路如图4所示。

图4 利用电阻电压与电源电压同相法测谐振

改变交流电源的频率，将示波器上的双踪波形通过横向展宽、纵向展高，观察双踪波形是否相交于横轴（即同相），如图5所示。

图5 电阻电压与电源电压相位比较

当两波形相交于横轴时，说明两电压同相，此时电路处于谐振状态，对应的交流电源的频率即为谐振频率。由于示波器波形可以展宽、展高，可放大观察两路信号相交处的局部特征，准确读出相位差异，因此该方法能很准确地测出谐振频率。同时，由RLC相频特性可知，在谐振频率时，相频特性曲线的斜率最大，即相位变化对频率变化最敏感，细微的频率变化将引起相位差明显变化。因此，该方法测量谐振频率精度高。电路品质因数越高，通频带越窄，电源频率在f0附近较窄的范围内变化时，电阻电压和电源电压的相位之差就会出现较大的变化，相位差对频率变化越敏感，测量越准确。

因此，该方法测量精度高，品质因数越高，该测量方法越准确。

1.4 相同电阻电压时的高低频率法

RLC串联电路谐振时，调低电源的频率，使电路失谐，当电阻电压下降为谐振时最大电压的0.707倍，此时测出的频率为下限频率fL；当调高电源的频率，同样使电阻电压下降为谐振时最大电压的0.707倍，此时测出的频率为上限频率fH，理论分析可以知道， f0和fL，fH有如下关系［11］：

因此可以通过测量fL和fH计算出f0。由RLC串联电路幅频特性可知（如图6所示），幅频特性曲线在fL和fH处斜率都较大，说明较小的频率变化就会观察到更大的电阻幅度变化。因此，可更准确地测出某一幅度所对应的频率。即fL和fH比f0有更高的测量精度。

图6 RLC串联电路幅频特性

对电路进行理论分析，当f=fL=14.605 kHz时，电阻电压下降为最大电压的0.707倍。交流电源频率变信号化范围为14.585 kHz～14.626 kHz时，电压在0.707倍附近变化1%，所以可以在14.585 kHz～14.626 kHz范围附件找到下限频率fL。同理可以在26.240 kHz～26.335 kHz范围附件找到上限频率fH。由于fL和fH比f0有更高的测量精度，所以通过测量fL和fH间接测量f0可获得更高的测精度。

事实上，通过理论推导，只要保证信号源输出的电压一定，将信号源的频率分别调高和调低，使电阻元件两端电压为一个相同的电压值（可以不是最大电压的0.707倍），记录此时的信号源的高低频率f1和f2，在这两个频率时电阻电压UR1和UR2大小相同，则电容电感总电压ULC1和ULC2也相同，总电抗也相同，因此有：

上式可变换为：

可以看出，谐振频率f0与f1和f2成等比关系。因此可通过测量电阻两端电压相同时的高低两个频率计算谐振频率。在上下限频率附近，测量最准确。

上述方法与最大电流、电压法相比，能更准确地测出下限频率fL和上限频率fH，从而更准确地计算出f0，精度可提高10倍左右。电路品质因数越高，电阻电压对频率变化越敏感，测出下限频率fL和上限频率fH就越准确，因此谐振频率测量越准确。

2 结束语

从以上分析可知，若串联谐振频率的测量方法不同，测量精度就不同。传统的最大电流、最大电压法测量谐振频率精度较低，对品质因数较低的电路，尤其不宜采用该方法。一般而言，由于1.2和1.3节所述方法都是用测量最小值得到谐振频率，即分别测量最小总电压和最小相位差，此时可以通过减小量程档来更准确观测，所以用1.2节和1.3节的方法测量精度更高，同时也比较方便，能更快速、更准确找到谐振频率。但对电阻很小、电感等效电阻较大的电路，1.2节的方法不宜采用。用1.4节所述方法测量精度居中，但要求进行计算，测量也更复杂。综上所述，对不同参数的电路，可以选择不同的测量方法，选择合理的测量方法，可大大提高测量精度。同时，在教学中，要求学生尝试用不同方法进行测量和比较，可培养学生勤于思考、勇于创新、精益求精、追求卓越的意识，能收到更好的教学效果。

参考文献

［1］张琦.RLC谐振电路的问题探究式教学方法［J］.大学教育，2013（4）:108-110.

［2］唐巍.电路实验教程［M］.北京:中国电力出版社，2005.

［3］刘竹琴.LRC串联谐振电路中Q与R关系的实验研究［J］.电子测量技术，2014，37（4）:9-11.

［4］陈星辉.测量RLC串联电路谐振频率的几种方法［J］.物理通报，2001（8）:31-32.

［5］周宦银.电子仪器共地常出现的测量错误研究［J］.中国现代教育装备，2006（9）:53-55.

［6］梅立坤.对RLC串联谐振电路中谐振频率测量方法的改进［J］.科协论坛，2010（12）:89-90.

［7］邱选兵.谐振频率测量试验方法研究［J］实验科学与技术，2008，6（6）:6-8.

［8］蔡敏.基于EWB的RLC串联谐振电路分析研究［J］.科技创新导报，2012（27）:104-106.

［9］赵琳.RLC串联谐振电路实验方法的研究与探索［J］.实验技术与管理，2013，30（6）:70-73.

［10］胡勇.通过误差修正改进RLC串联谐振实验［J］.高校实验室工作研究，2010（1）:66-69.

［11］周宦银.串联谐振电路实验中的几个问题［J］.中国教育技术装备，2006（9）:46-48.

Study on Measurement of Resonant Frequency of RLC Series Circuit Via Comparison

Zhou Huanyin， Shen Tingyun， Wen Qilin， Li Lirong， Xie Yanhui， Cao Jianfeng
College of Chemical Defense， Beijing， 102205， China

Abstract:Resonant frequency of RLC series circuit is usually measured by means of max current or max voltage. But the precision is usually low by this means. Especially for low quality factor circuits， resonant frequency can't be measured precisely. In this paper， after years of practice testing， some useful methods of measuring resonant frequency ware put forward， and these methods were compared and analyzed according to RLC series circuit's characters. The following conclusions were drawn. Different methods will lead different precision. Rational measurement method should be chosen for circuits of different component parameter. With this way， resonant frequency can be measured much more precisely.

Key words:RLC series circuit； resonant frequency； measuring methods； precision； comparison

收稿日期：2015-11-07

作者简介：周宦银，硕士，讲师。沈庭云，硕士，教授，系主任。

基金项目：2110工程建设教学改革项目支持。