FDI、空间溢出与中国工业全要素生产率——基于空间杜宾模型的研究

汪辉平，王美霞，王增涛

(1.西安交通大学 经济与金融学院,陕西 西安 710061；2.西安理工大学 经济与管理学院，陕西 西安710054)

FDI、空间溢出与中国工业全要素生产率

——基于空间杜宾模型的研究

汪辉平1，王美霞2，王增涛1

(1.西安交通大学 经济与金融学院,陕西 西安 710061；2.西安理工大学 经济与管理学院，陕西 西安710054)

摘要：采用1999-2013年省级面板数据，测算了中国工业TFP，并在此基础上构建空间杜宾模型，就FDI的空间溢出效应对工业TFP的影响进行研究。结果表明：FDI存在显著的空间溢出效应，FDI对工业TFP的影响既作用在区域内，也作用在区域间。FDI与本地区及相邻地区的TFP、技术进步显著正相关，且间接效应远大于直接效应；FDI与本地区技术效率改进显著正相关，与相邻地区技术效率改进负相关，且间接效应远小于直接效应。建议进一步加大FDI的引资力度，加强区域之间的交流与合作，实现资源共享，充分发挥FDI空间溢出效应。

关键词：外商直接投资；空间溢出；工业全要素生产率；空间杜宾模型

一、引 言

改革开放以来，外商直接投资(FDI)在中国迅速发展。截至2014年底，中国实际利用外资金额达1 195.6亿美元，并取代美国成为FDI的头号目的地。尽管在宏观层面上，FDI促进中国经济增长已经被广大学者所证实，但从微观层面来看，FDI是否存在技术溢出效应，是否促进了东道国工业企业全要素生产率(TFP)的提升，学术界对此并未定论[1]。理论上，FDI是一种稀缺的要素资源，能够带来先进的技术和管理经验，并通过产业示范与模仿、竞争、产业关联及人力资本流动等途径，实现要素资源的跨区域和跨行业配置，从而对东道国TFP形成溢出效应[2-3]。但在实证分析中，对于FDI与TFP的关系，通常存在两种截然相反的观点。一是认为FDI促进了TFP的提升。Fukao等对日本制造业、Souare对加拿大制造业、Fauzel等对毛里求斯制造业的研究都发现，FDI通过溢出效应、积累效应等促进了东道国的技术创新，从而显著提升了TFP水平[4-6]。程惠芳、严鹏飞、王兵、王滨、覃毅和张世贤等学者对中国的研究也都发现，FDI对中国工业的TFP增长具有显著的促进作用[7-10]。另一种观点则认为FDI抑制了东道国TFP水平的提升。Aitken和Harrison对委内瑞拉、Djankov和Hoekan对捷克、Ahmed对马来西亚的研究都发现，FDI对东道国内资企业的生产率具有显著的负面影响[11-13]。包群、刘瞬佳、蒋仁爱和冯根福等学者对中国的研究结论也与此大致相同[14-16]。

综上所述，与国外文献的研究结果相比较，国内文献得出的结论要乐观得多，大多认为FDI对TFP的影响显著为正。但现有研究存在着共同的局限性：将各地区看成同一个均质的整体，忽视了地区之间的交互作用。由于FDI存在空间溢出效应，一个地区的工业TFP不仅受到本地区FDI的影响，同时还受到相邻地区FDI的影响，影响程度受到地域限制[17]。那么，如果不考虑空间效应，采用常规的计量模型来估算，结果将会产生严重误差[18]。鉴于此，本文在考虑空间相关性基础上，运用1999-2013年中国省级面板数据和空间杜宾模型，深入探讨FDI及其空间溢出效应对中国工业TFP的影响。

二、中国工业TFP的核算

现有文献通常采用参数法和非参数法来核算TFP，参数法主要有索洛余值法、超越对数生产函数法、随机前沿生产函数法(SFA)等，非参数法则主要有基于数据包络分析(DEA)的Malmquist生产率指数法。由于非参数法不需要事先考虑具体的生产函数，可直接利用线性化给出边界生产函数与距离函数的估算，同时还能进一步将TFP值分解为技术效率改进和技术进步，便于对经济问题的深入探讨，因此，在当前的研究中得到广泛应用，故本文采用Malmquist-DEA生产率指数法对中国工业TFP进行核算。

本文以1999-2013年中国规模以上工业企业为样本，涉及到除去西藏以外的中国大陆30个省份，数据根据历年的《中国统计年鉴》、《中国工业经济统计年鉴》和《中国区域经济统计年鉴》等相关的统计资料整理得到。我们利用DEAP2.1软件计算Malmquist生产率指数，选择规模报酬不变，基于投入导向的DEA模型[19]。在计算过程中，会涉及到投入指标和产出指标，现分别介绍如下：

投入指标采用劳动投入和固定资本存量两个变量来表示。劳动投入采用各省规模以上工业企业年末从业人员数来表示。固定资本存量采用各省规模以上工业企业固定资产净值年平均余额来表示，并以1999年价格为基年，使用年固定资产投资价格指数对其进行折算。产出指标采用各省规模以上工业企业总产值来表示，同样利用工业产品出厂价格指数(IPPI)，将当年价的工业总产值折算为1999年不变价格的实际值。

经计算得到Malmquist指数后，再将其转换成TFP，按照程惠芳和陆嘉俊的方法，假定基年1999年TFP=1，则2000年的TFP可表示为1999年的TFP乘以2000年的Malmquist指数，2001年的TFP则可表示为2000年的TFP乘以2001年的Malmquist指数，以此类推可得到各省1999-2013年的TFP值[20]。根据估算结果，我们利用趋势图，从全国层面对FDI和工业TFP的相关性进行定性分析。从图1中可以看出，随着FDI的增加，TFP表现出明显的上升趋势，两者之间呈现正相关。

图1　人均FDI与TFP

三、模型设定和数据说明

(一) 基本模型设定

我们假设各地区的工业生产符合柯布—道格拉斯生产函数特性，构建模型如下：

Yit=ALitαKitβFDIitθ

(1)

式中Yit表示i地区t年的工业总产出，A为常数，Lit表示i地区t年的工业劳动投入，Kit表示i地区t年的资本投入，FDIit表示i地区t年的FDI。

lnTFPit=λ+θlnFDIit+εit

(2)

为避免遗漏变量所引起的内生性问题，在公式(2)的基础上，还需引入一些其他控制变量，分别为：地区开放程度、教育水平、工业聚集度、所有制结构、科研经费投入等，因此公式(2)可改写成：

(3)

其中Conait表示各控制变量。

(二)空间模型的构建

由于FDI存在空间溢出效应，那么地区i的FDI不仅对本地区的工业TFP产生影响，而且还可能对相邻地区的TFP产生影响。那么，根据Anselin和Elhorst等学者关于空间相关性的设定[21]310-330[22]，我们进一步构造空间杜宾模型(SDM)如下：

lnTFPit=λ+θlnFDIit+θ1WlnFDIit+

(4)

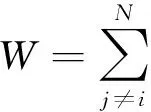
在公式(4)中，采用空间邻接矩阵来表示空间权重矩阵W，定义如下：

(5)

公式(5)中的i，j均为各地区单元编号，i,j∈[1,n]，n为地区单元个数。

为深入分析FDI对TFP的影响机制，我们进一步将工业TFP分解为工业技术效率改进(EC)和技术进步(TC)，按照公式(4)的形式，继续构建FDI与工业技术效率改进和技术进步的空间杜宾模型，公式如下所示。

技术效率改进：

lnECit=λ+θlnFDIit+θ1WlnFDIit+

(6)

技术进步：

lnTCit=λ+θlnFDIit+θ1WlnFDIit+

(7)

式中，ECit表示技术效率改进，TCit表示技术进步，其他参数含义与公式(4)中相同。

(三)变量选取与数据说明

为了实证检验FDI与中国工业TFP之间的定量关系，我们将FDI与TFP作为模型的核心变量进行考察，各变量选取如下：

全要素生产率(TFP)：作为被解释变量，是模型的主要考察变量，采用各省工业行业TFP来表示，已在前文中利用Malmquist生产指数法估算得到。

外商直接投资(FDI)：作为主要的解释变量，采用各省人均FDI这一衡量指标，数据来源于《中国统计年鉴》。

其他控制变量：地区开放程度(Open)采用各省贸易进出口总额与GDP的比值来表示，数据来源于《中国统计年鉴》。教育水平(Edu)采用各省每万人高校在校人数来表示，数据来源于各省统计年鉴。工业聚集度(Ind)采用各省工业总产值占全国工业总产值的比重表示，数据来源于《中国统计年鉴》。所有制结构(Soe)用各省国有企业就业人数占该地区总就业人数的比重来表示，数据来源于各省统计年鉴。科研经费投入(RD)用各省R&D经费投入占GDP比重来表示，数据来源于《中国科技统计年鉴》。缺失数据采用插值法进行估算，各变量的描述性统计见表1所示。

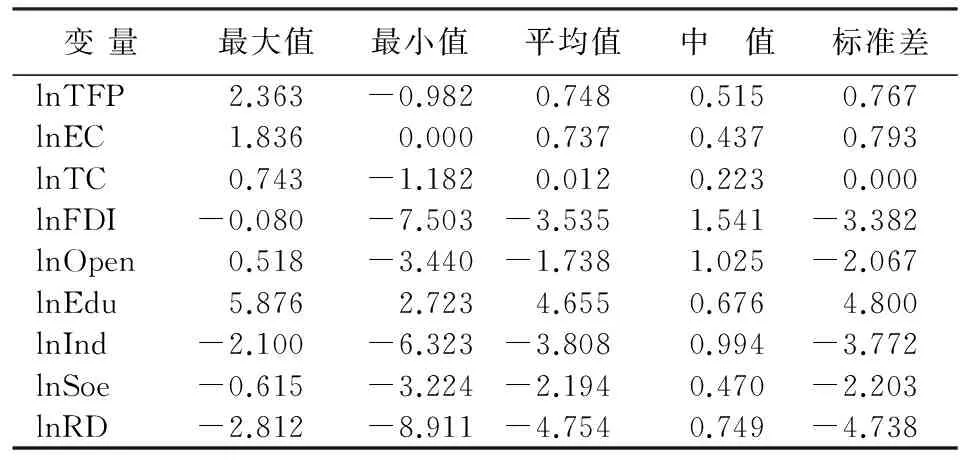
表1　各变量的描述性统计

四、实证分析

(一)非空间面板模型的估计

为了判断各变量之间是否存在空间相关性，我们将首先不考虑空间因素，采用OLS方法对模型进行参数估计，借鉴Elhorst的方法，分别针对TFP、EC和TC，估算空间固定效应和时间固定效应两种不同方程下的回归系数[23]。估算结果见表2。从表中可以看出，与时间固定效应方程相比，空间固定效应方程中估计系数更为显著，且R2值更大，相对来说模型的拟合程度较好，故模型采用空间固定效应较为合适。

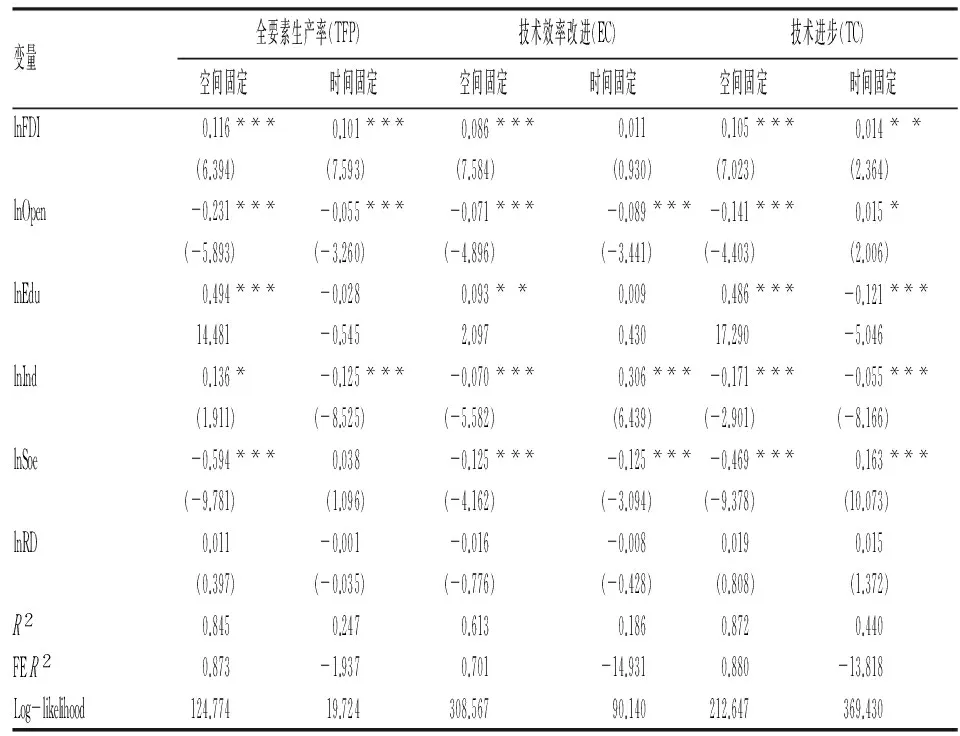
表2　非空间面板模型的估计结果

注：***、**和*分别表示在1%、5%和10%的水平上显著。下表同。

对TFP的回归结果显示，FDI的影响系数为0.116，且在1%的水平上显著，FDI显著促进了中国工业TFP的提升，反映FDI流入所带来的竞争、示范、模仿、人员流动以及产业关联效应，对中国工业TFP产生正向的技术溢出效应；教育水平、工业聚集度、科研经费投入与TFP呈正相关，地区开放程度、所有制结构与TFP呈负相关。对EC的回归结果显示，FDI与工业技术效率改进呈正相关，且在1%的水平上显著，表明FDI的大规模进入促进了中国工业技术效率的改进；教育水平与技术效率改进呈正相关，地区开放程度、工业聚集度、所有制结构、科研经费投入与技术效率改进负相关。对TC的回归结果显示，FDI与工业技术进步呈正相关，在1%的水平上显著，表明FDI所带来的先进技术被中国工业企业所吸收，促进了企业自主创新能力和技术进步；教育水平、科研经费投入与技术进步呈正相关，地区开放程度、工业聚集度、所有制结构与技术进步负相关。

(二)空间相关性检验

在空间计量模型中，主要采用两个基本模型来描述空间效应中的自相关和差异性，分别为空间滞后模型(SAR)和空间误差模型(SEM)，可以通过检验是否存在上述两种模型，来判断变量之间是否存在空间相关性。因此，我们将进一步采用LM方法进行假设检验，设定两个原假设：不存在空间滞后模型(SAR)和空间误差模型(SEM)，检验结果见表3。

LM检验显示，在空间固定效应和时间固定效应方程中，两种原假设都被拒绝，即模型存在空间相关性。再进一步进行 Roust LM检验，TFP回归模型中，空间固定效应和时间固定效应方程均拒绝原假设，在EC和TC回归模型中，只有时间固定效应方程无法拒绝不存在空间误差模型的假设，即模型存在空间相关性。因此，上述检验结果充分说明空间模型比非空间模型更为适合。

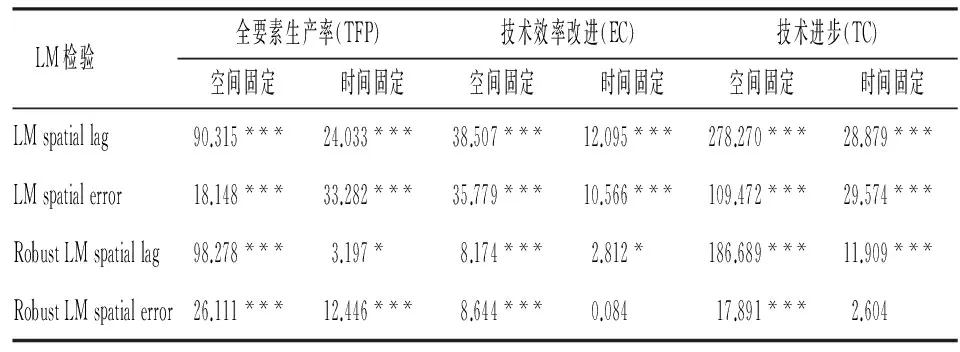
表3　LM检验结果

(三)LR和Wald检验

LR和Wald检验的目的，主要是判断空间滞后模型(SAR)、空间误差模型(SEM)和空间杜宾模型(SDM)中，哪一个更适合本研究。检验结果见表4所示。对于TFP、EC、TC三种回归模型，SAR、SEM的假设均在1%的显著水平上被拒绝，即SAR和SEM模型皆不适合，故本文采用SDM模型。

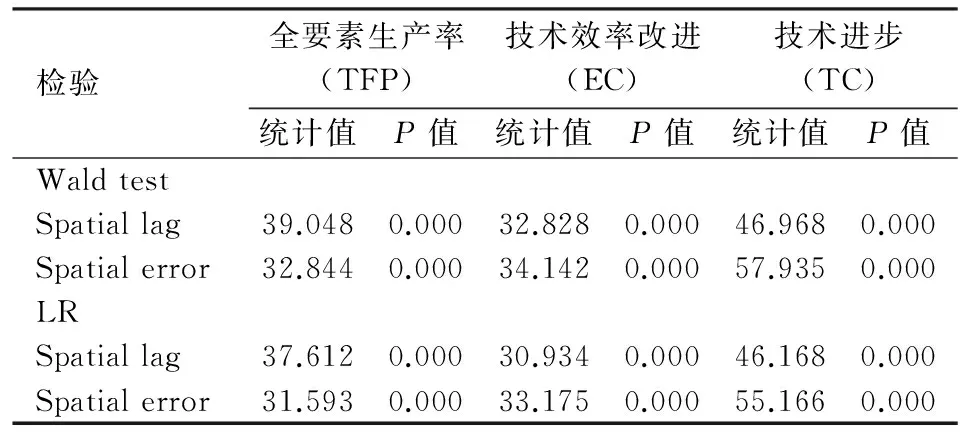
表4　空间模型的LR和Wald检验

(四)空间杜宾模型(SDM)的估计和分析

在考虑空间因素的基础上，参考Elhorst的方法，利用Matlab软件和极大似然估计法(MLE)，分别对模型(4)、(6)、(7)进行参数估计，针对TFP、EC、TC三种不同SDM模型的估计结果如表5所示。

表5　SDM模型的估计结果

对TFP的估计结果显示：因变量TFP的空间滞后项的系数为0.307，且在1%水平上显著，说明邻近地区TFP对本地区TFP产生显著的正向空间溢出效应。FDI的影响系数为0.064，在1%的水平上显著，且明显小于表2中的0.116，这表明若不考虑空间效应会高估FDI对TFP的影响。相邻地区FDI对本地区TFP的影响系数为0.134，在1%的水平上显著。由此可见，FDI对TFP同时在地区内和地区间产生溢出作用，而且相邻地区FDI对本地区TFP的空间溢出效应还要大于本地区FDI。其他控制变量：本地区和相邻地区的地区开放程度与TFP都呈现负相关；本地区和相邻地区的教育水平与TFP都呈正相关；本地区的工业化聚集度与TFP显著正相关，而相邻地区的工业化进程与之显著负相关；本地区和相邻地区的所有制结构与TFP都显著负相关；本地区和相邻地区的科研经费投入与TFP都呈负相关，但不显著。

对EC的估计结果显示：因变量EC的空间滞后项的系数为0.569，且在1%的水平上显著，说明邻近地区的技术效率改进对本地区技术效率改进的正向空间溢出效应明显。本地区FDI的影响系数为0.104，相邻地区FDI的影响系数为-0.022，这表明FDI在区域内促进了技术效率改进，但在区域间却抑制了技术效率改进。

对TC的估计结果显示：因变量TC的空间滞后项的系数为0.727，且在1%的水平上显著，说明邻近地区技术进步对本地区技术进步产生明显的正向空间溢出效应。本地区FDI 的影响系数为0.023，相邻地区FDI的影响系数为0.034，说明FDI在地区内和地区间都促进了技术进步。

(五)直接效应、间接效应和总效应

对于SDM模型来说，由于自变量存在空间滞后项，采用点估计值难以反映自变量的边际效应，为了准确区分FDI对本地区和相邻地区TFP的影响程度，我们将进一步估算各自变量的直接效应、间接效应和总效应[24]75-98[25]。其中，直接效应反映本地区自变量对因变量的溢出效应，间接效应反映本地区自变量对相邻地区因变量的溢出效应，总效应则为两者之和。估算结果见表6。与表2中的非空间面板模型估计结果相比，表6中的直接效应数值偏大或偏小，这说明非空间面板模型由于没有考虑空间溢出效应而存在高估或低估的问题。

对TFP的估计结果显示：FDI的直接效应为0.076，在1%的水平上显著。由于存在因变量和自变量的空间滞后项，直接效应中还包含了邻近地区的反馈效应，即邻近地区TFP和各自变量对本地区TFP的影响，反馈效应值应为表5中的估计系数与表6中各自变量的直接效应的差值，那么FDI的反馈效应则为-0.012。地区开放程度、教育水平、工业聚集度、所有制结构、科研经费投入的反馈效应分别为0.012、0.029、0.042、0.027、0.003。FDI的间接效应为0.210，要远大于直接效应。可见，FDI在地区内和地区间都对工业TFP产生正向溢出效应。

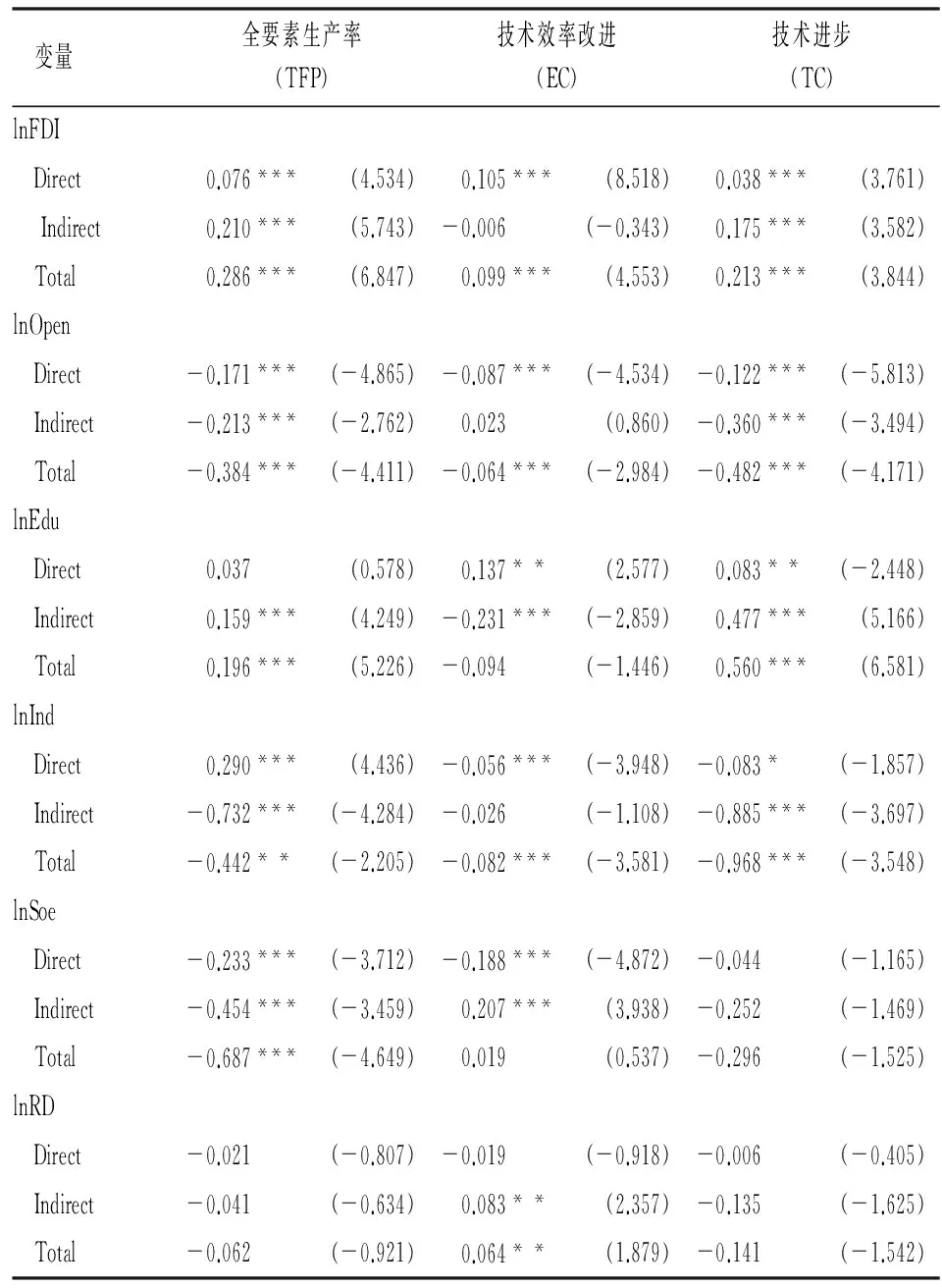
表6　直接效应、间接效应和总效应

对EC的估计结果显示：FDI的直接效应为0.105，在1%的水平上显著。同样，直接效应中还包含了邻近地区技术效率改进和各自变量对本地区技术效率改进的影响，FDI的反馈效应则为-0.001。地区开放程度、教育水平、工业聚集度、所有制结构、科研经费投入的反馈效应分别为0.004、-0.037、-0.005、0.034、0.014。FDI的间接效应为-0.006，要远小于直接效应，且不显著，说明FDI对邻近地区技术效率改进的影响不显著。

对TC的估计结果显示：FDI的直接效应为0.038，在1%水平上显著。同样，直接效应中还包含了邻近地区技术进步和各自变量对本地区技术进步的影响，FDI的反馈效应则为-0.015。地区开放程度、教育水平、工业聚集度、所有制结构、科研经费投入的反馈效应分别为0.031、0.068、0.077、0.022、0.011。FDI的间接效应为0.175，要远大于直接效应。可见，FDI在地区内和地区间都对工业技术进步产生正向溢出效应。

五、结论

当前关于FDI对中国省域工业行业生产效率影响的研究大多忽视了区域之间的空间相关性，本文在考虑空间因素作用的基础上，构建空间杜宾模型，并利用1999-2013年中国规模以上工业企业的省级面板数据，实证检验FDI空间溢出效应对中国工业TFP、技术效率改进和技术进步的影响，结论如下：

1．FDI对中国工业TFP的空间溢出效应既产生在地区内，也产生在地区间，表明一个地区的FDI不仅能刺激本地区TFP提升，而且还能带动和提升相邻地区的TFP水平。

2．FDI对本地区的工业技术效率改进具有显著的促进作用，表现为地区内的正面溢出效应，但FDI对相邻地区工业技术效率改进具有明显的抑制作用，表现为地区间的负面溢出效应。

3．FDI对本地区和相邻地区的工业技术进步都具有显著的促进作用，在地区内和地区间都呈现出正面溢出效应，同时也表明FDI的空间溢出效应主要是通过促进技术进步来提升TFP水平。

该研究结果为中国FDI引资政策和区域工业发展提供了如下启示：

1．积极正确认识到FDI的空间溢出效应及其对工业TFP的正向促进作用，进一步扩大区域对外开放程度，加大FDI的引入力度，重视FDI对技术进步和TFP的引领和推动作用，针对不同区域制定差异化的引资政策。

2．进一步加强区域之间的交流与合作，消除区域之间的行政壁垒，发挥相邻地区FDI的空间溢出效应，实现市场、人才、资本等资源的共享，推进区域协调发展。

参考文献：

[1]文军，于津平．贸易开放、FDI与中国工业经济增长方式——基于30个工业行业数据的实证研究[J]．经济研究，2012(8)．

[2]Almeida P, Kogut B. Localization of Knowledge and Mobility of Engineers in Regional Networks [J]. Management Science, 1999,45(7).

[3]Saggi K. Trade, Foreign Direct Investment and International Technology Transfer: A Survey[J]. The World Bank Research Observer, 2002, 17(2).

[4]Fukao K, Ito K, Kwon H. Do out-in M&As Bring Higher TFP to Japan? An Empirical Analysis Based on Micro-data on Japanese Manufacturing Firms[J]. Journal of the Japanese and International Economies, 2005, 19(2).

[5]Souare M. Productivity Growth, Trade and FDI Nexus: Evidence from the Canadian Manufacturing Sector[J].The Journal of Technology Transfer,2013,38(5).

[6]Fauzel S, Seetanah B, Sannasee R V. Productivity Spillovers of FDI in the Manufacturing Sector of Mauritius. Evidence from a Dynamic Framework[J]. Journal of Developing Areas,2015,49(2).

[7]程惠芳.国际直接投资与开放内生经济增长[J].经济研究，2002(10).

[8]严鹏飞，王兵.技术效率、技术进步与生产率增长：基于DEA的实证分析[J].经济研究，2004(12)．

[9]王滨. FDI技术溢出、技术进步与技术效率——基于中国制造业1999-2007年面板数据的经验研究[J].数量经济技术经济研究，2010(2).

[10]覃毅，张世贤. FDI对中国工业企业效率影响的路径——基于中国工业分行业的实证研究[J].中国工业经济，2011(11).

[11]Aitken B, Harrison A. Do Domestic Firms Benefit from Foreign Direct Investment? [J]. American Economic Review,1999,89(3).

[12]Djankov S, Hoekman B. Foreign Investment and Productivity Growth in Czech Enterprises[J]. World Bank Economic Review,2000, 14(1).

[13]Ahmed E M. Are the FDI Inflow Spillover Effects on Malaysia's Economic Growth Input Driven?[J].Economic Modelling,2012,29(4).

[14]包群，赖明勇.FDI技术外溢的动态测算及原因解释[J].统计研究，2003 (6).

[15]刘舜佳. 国际贸易、FDI和中国全要素生产率下降——基于1952-2006年面板数据的DEA和协整检验[J].数量经济技术经济研究，2008(11).

[16]蒋仁爱，冯根福.贸易、FDI、无形技术外溢与中国技术进步[J].管理世界，2012(9) .

[17]Bode E, Nunnenkamp P, Waldkrich A. Spatial Effects of Foreign Direct Investment in US States[J]. Canadian Economics Association,2012,45(1).

[18]Baltagi B H, Peter E, Michael P. Estimating Models of Complex FDI:Are There Third-country Effects?[J]. Journal of Econometrics, 2007,140(1).

[19]汪辉平，王增涛，王美霞. 知识资本、空间溢出与中国工业全要素生产率[J].山西财经大学学报，2016(5).

[20]程惠芳，陆嘉俊.知识资本对工业企业全要素生产率影响的实证分析[J].经济研究，2014(5).

[21]Anselin L. Spatial Econometrics: Methods and Models[M]. Dordrecht:Kluwer Academic Publishers,1988.

[22]Elhorst J.Matlab Software for Spatial Panels[R]. Presented at the IVth World Conference of the Spatial Econometrics Association(SEA), 2010.

[23]Elhorst J P. Spatial Panel Data Models[J]. Springerbriefs in Regional Science, 2009, 87(2).

[24]Lesage J P, Pace R K. Advances in Econometrics: Spatial and Spatiotemporal Econometrics[M]. Oxford:Elsevier Science, 2004.

[25]朱福林.社会资本、国际R&D溢出与全要素生产率[J].西安财经学院学报，2015(3).

(责任编辑：张治国)

FDI, Spatial Spillover and Total Factor Productivity of Chinese Industry: A Study Based on Spatial Durbin Model

WANG Hui-ping1, WANG Mei-xia2, WANG Zeng-tao1

(1.School of Economics and Finance, Xi`an Jiao Tong University, Xi′an 710061,China;2.School of Economics and Management, Xi`an University of Technology, Xi′an 710054,China)

Abstract:In this paper, we calculate the industrial TFP in China by using provincial panel data of 1999-2013, and study the effect of FDI on industrial TFP by constructing Spatial Durbin Model. The results show that spatial spillover effect of FDI is significant, and the effect of FDI on industrial TFP is not only in intra-region but also inter-region. FDI is significantly positively related to the TFP and technology progress in the local and adjacent areas, and the indirect effect is far greater than direct effect. FDI is significantly positively correlated with technology efficiency improvement in the local regions, and negatively related to technology efficiency improvement in the adjacent regions. The indirect effect is far less than direct effect. The suggestion is to further increase investment of FDI, and strengthen exchanges and cooperation between the regions, to achieve resource sharing and fully exert the spatial spillover effect of FDI.

Key words:FDI; spatial spillover; industrial TFP; spatial durbin model

收稿日期：2016-01-22；修复日期：2016-04-17

基金项目：教育部哲学社会科学研究重大课题攻关项目《新常态下中国经济运行机制的变革与中国宏观调控模式重构研究》(15JZD012)；西安理工大学社会科学基金一般项目《企业家才能误配与中国经济增长研究》(107- 211425)；西安理工大学博士科研启动基金项目《基于产权、市场结构双约束下的外资银行进入对中国商业银行效率的影响研究》(105-451115003)

作者简介：汪辉平，男，安徽安庆人，博士生，研究方向：区域经济，空间计量学；

中图分类号：C812∶F403

文献标志码：A

文章编号：1007-3116(2016)06-0044-07

王美霞，女，内蒙古鄂尔多斯人，经济学博士，讲师，研究方向：区域经济；

王增涛，男，陕西渭南人，教授，博士生导师，研究方向：国际贸易。

【统计应用研究】