分布式系统中的时钟同步新方法∗

李滚牛梦洁 柴阳顺 陈鑫 仁艳秋

(电子科技大学航空航天学院 成都 611731)

分布式系统中的时钟同步新方法∗

李滚†牛梦洁 柴阳顺 陈鑫 仁艳秋

(电子科技大学航空航天学院 成都 611731)

时间同步技术广泛应用于飞行器编队以及星座自主导航等方面.在网络化时钟同步应用中,网络中每个观测节点之间未必互联互通,因此,在某节点只能获取相应单个邻居节点的时钟测量信息而不能获得其他节点时钟测量信息的情况下,如何实现网络系统的高精度时间同步是个难点.针对网络节点只能获得单个邻居节点时钟测量信息的情况下,提出了一种实现网络系统中时钟高精度同步的方法.将每个时钟看作网络系统中的节点,首先定义了不同的分布式系统拓扑结构,在此基础上,分别设计了无主钟(参考时钟)、有主钟(参考时钟)和网络系统中存在固定通信时延的时钟同步控制算法.通过稳定理论分析和仿真实验验证了所设计时钟同步协议的正确性.

天体测量学:时间,方法:数据分析

1 引言

时间同步技术广泛应用于飞行器编队以及星座自主导航等方面[1−5].在卫星导航技术应用中,星座自主导航能力具有越来越重要的作用,其中星座网络中的自主时间同步和信息交换技术不可或缺[6−9].在飞行器编队飞行控制中,飞行器间的相对或者绝对定位、通信都需要相互的时间同步,整个飞行器编队需要一个统一的时间参考基准.另外,各个时间实验室的国际高精度时间比对是最为典型的分布式时间同步应用的例子[2−3].因此,各类时间同步应用可以概括为不同拓扑结构的分布式系统中的时间同步问题.以前的研究一直集中在系统中的每个节点可以获得系统中的全局时钟信息,或者固定节点之间的时间同步,而对于一个具有多个节点的复杂网络系统,如果每个节点只知道相邻一个或两个节点的信息(并且保证每个节点都和一个邻居节点连通),针对这一问题,如何实现网络系统中的时钟同步,目前的研究并不多.Bolognani等[10]基于网络群体系统,应用随机线性系统理论研究了时间同步技术.该文假设多个时钟都具有不同的钟差和钟速,时钟之间的通信通过非对称的广播协议,并通过设计控制协议,进而调节时钟参数进行时钟的同步控制,使得网络中的时钟达到同步.基于文献[10-12]的启发,本文分别考虑了网络群体系统中无参考时钟、含有一个参考时钟以及时钟系统中存在时延干扰情况下的时间同步方法.无参考钟的系统是指网络群体中没有主钟,每个节点处于同等地位.有参考钟的时钟同步技术是指系统中有一个或者多个主钟,在此系统中,时钟同步的控制就是实现其他子时钟最终能够与参考时钟完全同步,即实现绝对时钟同步,而如果子时钟能够与参考时钟保持固定的钟差不变,则可实现相对时钟同步.

2 时钟模型

考虑一个具有n台钟的分布式系统,对于其中的任意1台钟,记作第i台钟,其时钟模型可以近似表示为:

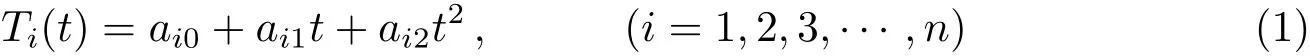
其中,Ti(t)表示时钟i在t时刻的时钟读数,ai0、ai1、ai2分别为时钟i的钟差、钟速、钟漂.这样一个模型称为2阶模型.有时候,我们称这n台钟组成的分布式系统为网络群体系统,网络群体系统的通信拓扑结构用图论中的图表示,本文用图G表示,图中的每个节点代表1台时钟,第i个节点所代表的时钟模型用(1)式表示.这里的时钟可以是目前常见的各类时钟,如铷原子钟、铯原子钟等.

本文重点以卫星星座时间同步应用为背景,由于目前GNSS(G lobal Navigation Satellite System)中的空间钟性能比较好,即在实际的星座网络中的自主时间测量中,钟漂的影响很小,基本可以忽略,因此时钟模型由(1)式退化为(2)式,这是一个线性模型,称为1阶模型.

本文首先研究基于1阶模型的分布式系统中的时间同步方法,对于时钟模型为非线性模型的2阶系统,另文研究.为方便,将该1阶模型对应的系统称之为1阶网络群体系统,为不失一般性,其动态方程可表示为:

xi(t)为时钟i在t时刻的状态,Δi(t)为第i台时钟的内部协同控制协议.可以把上述时钟系统看作1阶网络群体系统,Ti(t)就为第i台钟的时钟状态,为方便,则时钟同步协议表示为:

本文将1阶网络群体系统的协同控制问题应用到时钟同步中,使网络群体系统协同控制的应用更加具体化,对解决系统的时钟同步有着重要的研究意义.

3 分布式系统中的时钟同步

本节分3种网络拓扑结构重点分析讨论其时间同步协议的设计及稳定性.首先考虑一个由n台钟组成的分布式系统,每台钟的地位是平等的,即没有所谓的主钟或者参考钟,其目的是使这个网络系统中的时钟调节到状态一致,在实际应用中可以用一个纸面时间尺度.

3.1 分布式同步的优点

由于通信技术的迅猛发展,很多网络系统的规模非常庞大,并且内部组成要素之间的相互关系相当复杂.就时间同步问题而言,对于这样的复杂系统,利用传统的方法实现网络节点之间的时间同步效率较低.为降低复杂系统中时间同步的难度,本文选择了分布式处理的策略,这主要会带来如下几点好处:一是减少了集中式处理方式中的中心节点处理所带来的大量计算;二是减少了对通信链路的依赖性,相比而言具有更高的计算效率、更快的执行速度和更大的冗余度,且对于海量信息和大规模系统性能处理具有优势;三是由于每一个节点都被平等地看作一个能够智能处理和分发信息的对象,它们通过局部的相互作用可完成单个节点或多个节点集中处理所不能完成的任务;四是当采用分布式处理方式时,不会出现由于集中式中中心节点一旦出现问题从而导致整个系统出现同步失败的结果.由于其具有自主性和分布式的特点,这多个节点往往通过分布式的相互协作,形成规则有序的协同运动,如一致、编队、同步等.

基于分析可知:集中式同步方法是将观测时钟信息和计算任务都集中在以某时钟为中心的节点上,想要达到所有时钟的整体同步,则选取的中心始终需要与其余时钟都进行信息交互,且其余两两时钟间没有信息传递,中心节点承担了大量的计算工作量,这将会降低网络群体的同步性能.此外,当中心时钟节点受到外界干扰或是失联,则会导致整个网络群体系统同步失败.

分布式同步方法中没有中心节点,每个时钟都独立运行,因此可以消除集中式同步方法中中心节点失效导致整体系统同步失败或是单节点失效导致同步性能大幅度降低的缺点.并且分布式同步中时钟节点只需观测与之相邻的时钟节点信息并进行信息交互,因此减少了时钟节点间信息传递的工作量.

为进一步说明本方法带来的优势,假设有5台时钟组成的分布式网络群体.其中,图1中(a)、(b)、(c)采用分布式策略,(d)、(e)、(f)采用集中式分布策略且节点1为中心节点.

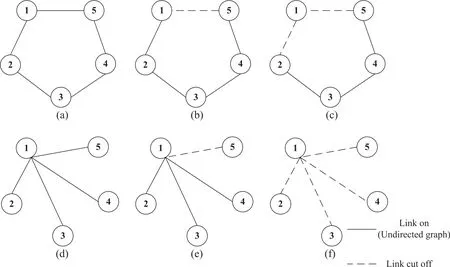
图1 分布式和集中式同步的比较Fig.1 The com parison of d istribu ted synch ron ization and centralized synch ronization

分布式处理方法与传统处理方法相比,有3个优点.

首先从计算复杂度上来说,其中图(a)、(d)为正常情况下两种分布方式的结构图.由图1可以看出,就节点1而言,图(a)的计算量仅与相邻节点2(5)进行信息交互处理,而图(d)中节点1却与节点2、3、4、5进行信息交互处理,这极大地增加了计算量.

其次,从链路的依赖性来说,图(b)较之于图(e)来说,同时都切断了节点1与5之间的通路,但这并不影响图(b)中所有节点的信息交互,但图(e)的节点5却彻底失去了与中心节点1的信息交互,不能够达到状态同步,即切断其中1个节点,网络拓扑改变,影响较大.

最后,从节点出错失联的影响结果看,图(c)和(f)都是节点1出现故障出错,但图(c)由于不依赖特殊节点,所以仅仅是节点1的缺失并不影响最终的状态同步,而图(f)中节点1的失联缺失会导致整个系统同步失败.

3.2 无参考钟的网络群体时钟同步

3.2.1 控制协议设计

假设有n台时钟组成的分布式网络群体时钟系统,每个时钟看作无向图G的节点,假设网络拓扑结构固定不变,且网络群体间不存在通信时延,则可设计控制协议为:

其中,Δi(t)为网络群体时钟同步控制协议,Ti(t)为第i台时钟的时钟读数(实际观测量), ψij表示系统的邻接矩阵元素且ψij≥0,若两台时钟可以通信,则ψij=1,否则ψij=0.若令状态变量α=[T1,T2,···,Tn]T,则存在矩阵B=0,C=1,使网络群体时钟系统的闭环动态方程为:

其中,L为系统拉普拉斯矩阵,In表示n阶单位阵,⊗为K ronecker积.

如果对于任意的i,j∈I=1,2,···,n满足:

则称无参考时钟的网络群体系统实现了时钟同步.

3.2.2 稳定性分析

一组定结构的分布式网络群体时钟系统,如果网络拓扑结构G连通,则利用协议(5)式,网络群体可以实现时钟同步.

可知,正定矩阵L的特征根可表示为0＜λ1＜λ2≤···≤λn.那么存在正交矩阵W∈Rn×n,使得:

进而有

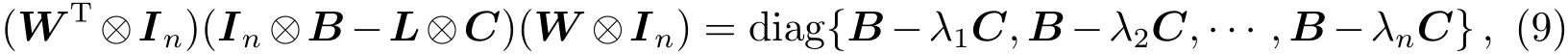
可以进一步得到B−λiC的特征多项式为

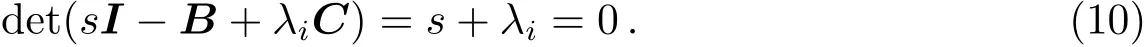
不难发现,s=−λi＜0.可见系统的特征根均具有负实部,即该控制系统是稳定的,可以实现时钟同步.

3.2.3 数值算例

假设1阶分布式网络系统的拓扑结构如图2所示,为简单起见,选择n=8台时钟组成的分布式系统,每个节点代表1台时钟.拓扑结构的边表示节点间的通信约束,如果节点之间有路存在,则可以进行时钟同步,反之则不能进行通信.实际中表示的物理意义是,这8台钟中,每台钟只能观测到其邻居节点的信息,而观测不到系统所有钟的观测信息.因此问题归结为只能观测到局部时钟信息的系统中的时间同步问题,只有相邻的钟之间可以传递其时钟测量数据,其他钟之间是不连通的.由图2可知,每个个体(钟)只能与它的邻居节点进行通信.为了便于观察结果,对节点之间的钟差及节点的A llan方差的仿真采用非对称坐标系,文中其他未进行说明的均为线性坐标系.

图2 无参考钟网络系统的拓扑结构Fig.2 The topo logy of the netw ork system withou t a reference clock

按照控制协议(5)式,如果有8台GPS星载钟的时钟数据,假设其拓扑结构如图2所示(并不是实际的星座拓扑结构),我们提取某天的GPS星历数据中的钟差参数(PRN21、PRN27、PRN5、PRN25、PRN9、PRN31、PRN16、PRN29)如下所示:

这时,该问题便成为已知网络群体的初始钟差和钟速情形下的时间同步问题.时钟同步的精度与仿真的步长有关系,仿真步长越小则精度越高,仿真中均设置仿真步长为可变步长,最大仿真步长表示为tepm.设仿真时间为50 s,最大仿真步长为tepm=0.1 s,网络群体的时钟状态序列如图3所示.应用协议(5)式可见:网络群体系统最终能够实现时钟的协同控制.时钟的观测序列的A llan方差如图4所示,图中τ为时间间隔.图5为此时钟速的序列图,由图5可见,8台时钟钟速最终能够实现一致.

图3 无参考钟网络系统的时钟观测序列F ig.3 The clock sequence of the netw ork system withou t a reference clock

图4 无参考钟网络系统的时钟观测序列的A llan方差Fig.4 The A llan dev iation of clock sequence of the netw ork system withou t a reference clock

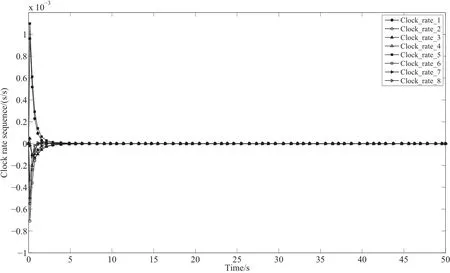
图5 无参考钟网络系统的钟速状态序列Fig.5 The clock rate sequence of the netw ork system without a reference clock

图6为节点1与节点2之间的钟差随时间的变化,从图6可以看出,当仿真时间结束时,同步精度到达纳秒级.

图6 tepm=0.1 s时,节点1与节点2的钟差Fig.6 The clock d ifference betw een node 1 and node 2 for tepm=0.1 s

3.3 有参考时钟的网络群体时钟同步

下面我们考虑一个由n台钟组成的分布式系统,其不同点是存在一个参考时钟即主钟(Master clock),且其他钟都不是孤立的,至少有一个与主钟相连通,最终和主钟同步.

3.3.1 控制协议设计

针对有参考时钟的网络群体系统,定义无向图˜G,含有n+1个节点,其中节点n+1为参考时钟,其他的1,2,···,n为子时钟.如果由所有子时钟所组成的图是无向连通的且有路到主时钟,则称图˜G是连通的.定义一个矩阵˜A∈Rn×n为˜G中参考时钟的邻接矩阵,其对角元素为di,di=ψi0.如果节点0与节点i邻接,则ψi0＞0,否则ψi0=0.

如果网络群体系统对于任意i,j∈I均有

则称具有参考时钟的网络群体系统实现了时间同步.由(11)～(12)式可设计控制协议:

其中,Δi为有参考时钟情况下的网络群体时钟同步控制协议,Ti(t)、Tj(t)为子时钟的卫星钟读数,T0(t)为参考时钟的卫星钟读数.

若记ξi=Ti(t)−T0(t),η=[ξ1,ξ2,···,ξn]T.利用协议(13)式,网络群体系统可表示为:

3.3.2 稳定性分析

考虑固定拓扑结构的时钟系统,且拓扑结构连通.若有对称正定矩阵P∈R,使得

则网络群体系统(13)式能够实现有参考钟系统的时钟协同控制.为系统(13)式定义一个公共的李亚普诺夫函数:

其中,P=PT∈R为正定矩阵.计算V(t)的导数为:

则含有参考钟的网络群体时钟系统能够实现时钟同步.

3.3.3 数值算例

如前述,假设有4台时钟数据(PRN18、PRN7、PRN13、PRN19)系统的拓扑结构如图7所示,假定所有边的权值为1.其中,节点0为参考钟,其他3个节点为子时钟.

图7 有参考钟网络系统的拓扑结构Fig.7 The topology of the netw ork system with a reference clock

按照(13)式,参考时钟的初始钟差和钟速分别为a00=2,a10=−0.46175328741× 10−11,其他子时钟的初始钟差和钟速分别为

在此基础上,可以给出含有参考时钟的网络群体系统的时钟状态序列,仿真时间为4 500 s,仿真步长为可变步长,最大步长tepm=1 s.为了便于观察仿真结果,图8是截取了仿真时间前50 s的结果.由图8可见,应用协议(13)式,3台子时钟最终跟踪参考钟实现了时钟同步的控制.时钟的观测序列的A llan方差如图9所示.图10为此时各个时钟的钟速序列,由图10可见,其他3个子时钟最终和参考时钟的钟速实现状态一致.

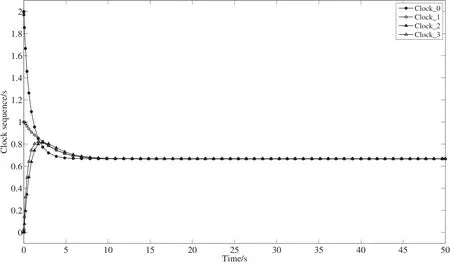
图8 tepm=1 s时,有参考钟网络系统时钟观测序列Fig.8 The clock sequence of the netw ork system with a reference clock for tepm=1 s

图9 有参考钟网络系统时钟观测序列的A llan方差Fig.9 T he A llan dev iation of clock sequence of the netw ork system with a reference clock

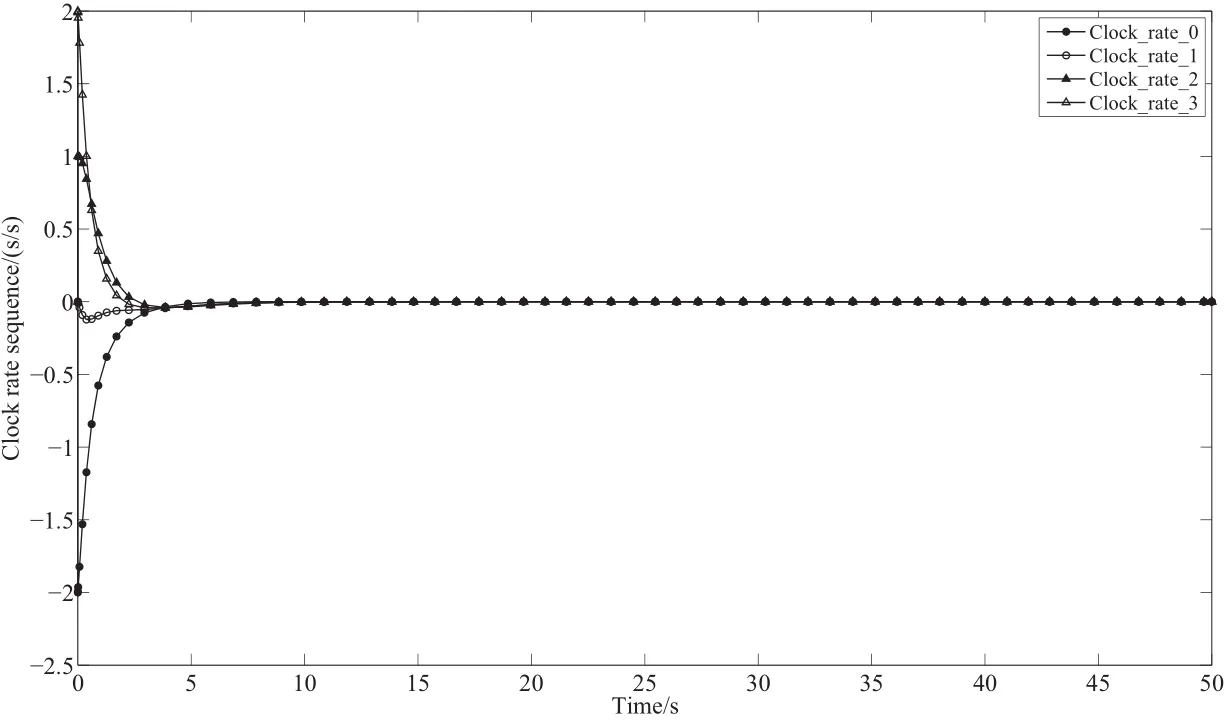
图10 tepm=1 s时,有参考钟网络系统钟速状态序列Fig.10 The clock rate sequence of the network system with a reference clock for tepm=1 s

假设系统的仿真时间为ts,图11为子时钟1和参考时钟0的时钟钟差随时间的变化,如果仿真时间为ts=4500 s时,最终子时钟1和参考时钟0的时钟钟差可以达到纳秒量级(9.7×10−9s).

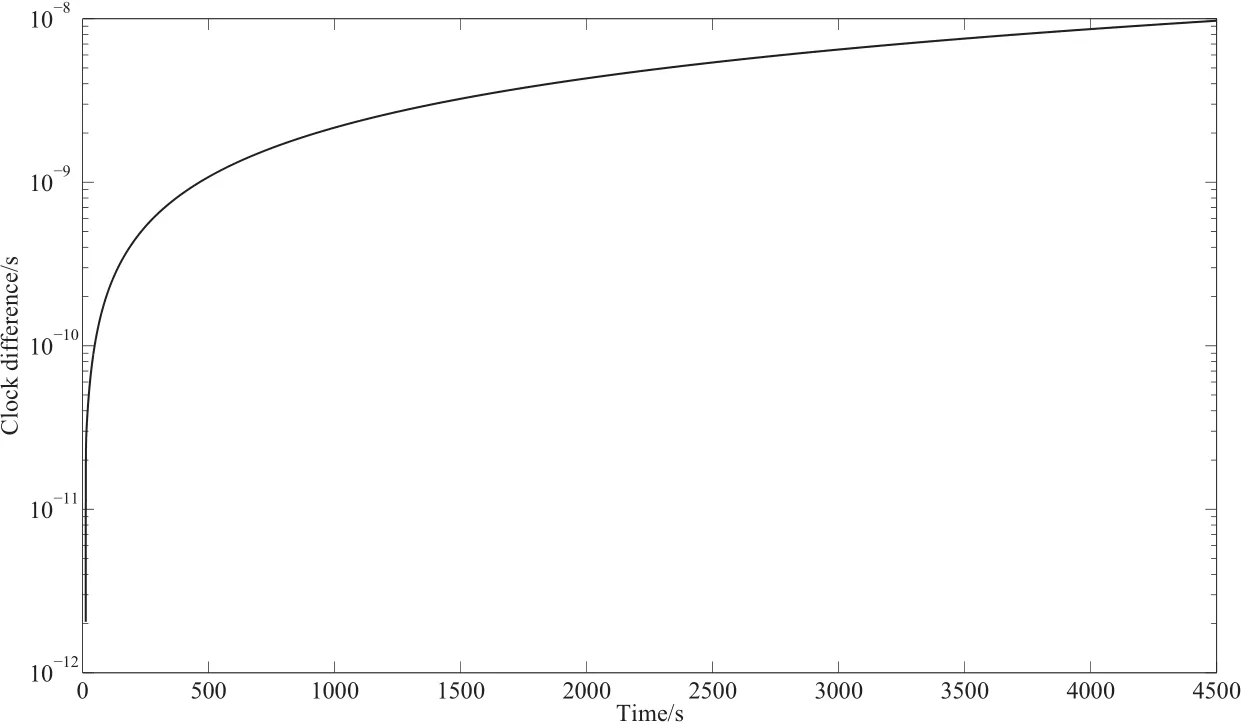
图11 ts=4500 s时时钟1与参考时钟0之间的钟差Fig.11 The clock d ifference betw een clock 1 and reference clock 0 for ts=4500 s

3.4 单时延网络群体时钟同步

最后考虑一个由n台钟组成的分布式系统,该系统没有参考钟,和第1种情形不同的是在系统中加入了固定的传输时延(随机时延协议更加复杂,这里暂时不考虑).

3.4.1 控制协议设计

在1阶网络时钟系统中,假设网络群体系统通信具有单时延,如果对于任意的i,j∈I满足

则具有单时延的网络群体系统实现了时钟同步.其中,Ti(t)是指在系统仿真时间t时的第i台时钟的时钟读数,τ为卫星间通信的单时延.

根据(18)式,在固定拓扑结构的情况下,设计控制协议为:

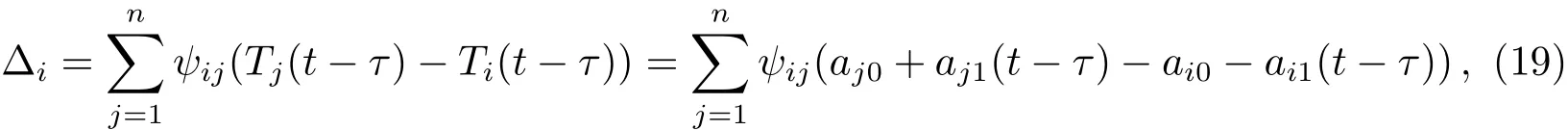
其中,Δi为单时延情况下卫星时间同步控制协议,ψij为卫星通信的邻接矩阵元素,aj0、ai0为初始钟差,aj1、ai1为卫星钟速.

若令状态变量δ=[T1,T2,···,Tn]T,则系统的闭环动态方程为:

3.4.2 稳定性分析

考虑定结构网络群体系统,假定网络拓扑结构是连通的,如果存在对称正定矩阵P、Q、R∈R2n×2n,使得

为了证明控制协议的正确性,定义李亚普诺夫函数为

则V(t)关于时间的导数为

因为δ(t−τ)=δ(t)−∫tt−τ˙δ(s)d s,利用舒尔补引理,有

3.4.3 数值算例

考虑网络群体系统中有5台时钟(PRN15、PRN22、PRN21、PRN27、PRN4),如图12所示的拓扑结构连接,假设边的权值为1,且每台时钟可以和邻接的时钟进行通信.按照控制协议(19)式,仿真步长为可变步长,最大步长为tepm=0.1 s.系统的仿真时间设置为ts=120 s,为了便于对结果的观察,仿真中随时间变化的时钟状态序列与钟速序列图截取合适的时间段来观察结果.每台时钟的初始钟差、钟速分别为

图12单时延网络系统的拓扑结构Fig.12 The top o logy of the netw ork system with one tim e delay

图13 为时钟系统时延τ=0.2 s时的5台时钟组成的网络群体系统的状态序列,从图13可以看出,应用协议(19)式各个时钟最终能够实现时钟同步.时钟的观测序列的A llan方差如图14所示.

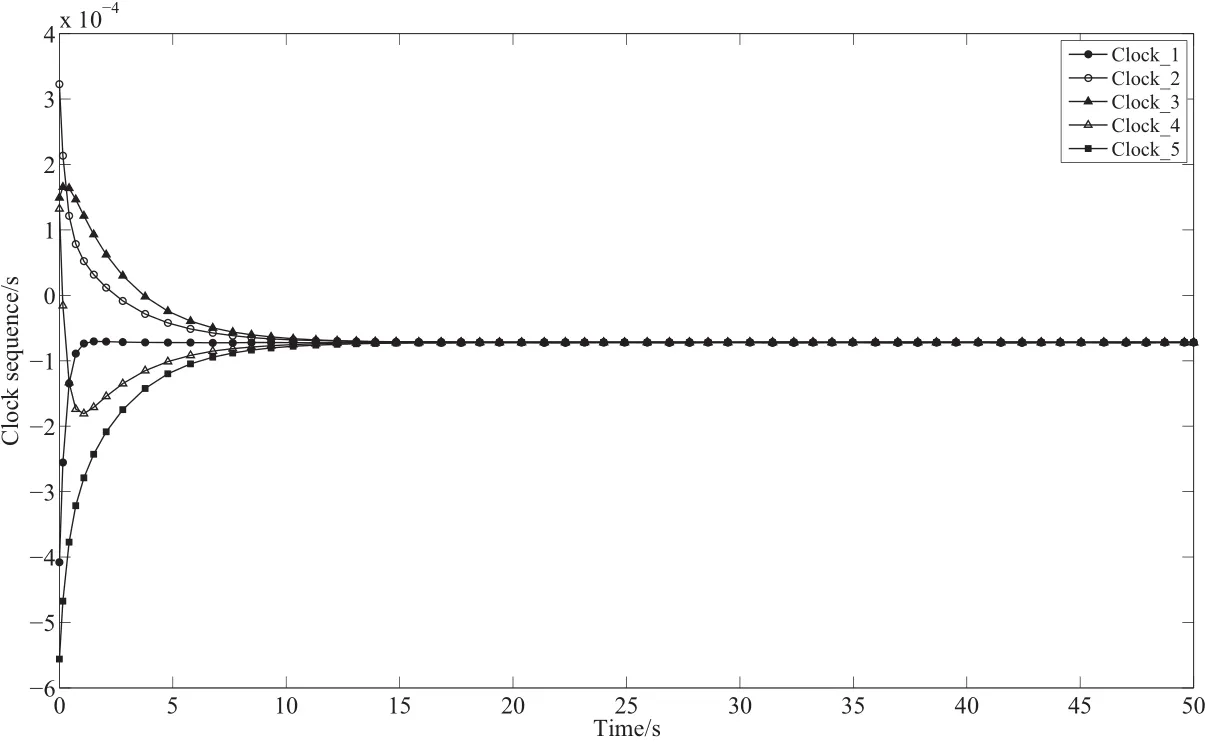
图13 τ=0.2 s时的单时延群体系统时钟观测序列Fig.13 The clock sequence of the network system with one tim e delay forτ=0.2 s

图14单时延群体系统的时钟观测序列的A llan方差Fig.14 T he A llan dev iation of clock sequence of the netw ork system with one tim e delay

图15 为系统的通信时延为τ=0.2 s时系统的钟速序列,由图15可见,随着仿真时间的增大,5台时钟的钟速最终能够实现状态一致.

图15τ=0.2 s时的单时延群体系统钟速状态序列Fig.15 T he clock rate sequence of the netw ork system with one tim e delay forτ=0.2 s

图16 为通信时延τ=0.2 s时,时钟4与时钟5之间的时钟钟差序列.由图16可知,在ts=120 s仿真时间内,两个时钟之间的钟差逐渐减小.由于初始钟差和钟速的影响,当仿真时间结束时,时钟同步的精度达到微秒级.持续增加仿真时间,则时间同步精度也可以达到纳秒级.

图16 τ=0.2 s时时钟4与时钟5的钟差Fig.16 T he clock d ifference betw een clock 4 and clock 5 forτ=0.2 s

另外,如果继续增大时延至τ=0.45 s时,图17和图18分别为5台时钟在仿真时间内的时钟状态序列以及钟速状态序列.可见,此时由5台时钟组成的网络群体系统已经发散,不能实现时钟同步.可见,时延的存在对系统时钟同步有着不可避免的影响,时钟系统对时延的承受是有上限的,这一问题需要进一步研究.

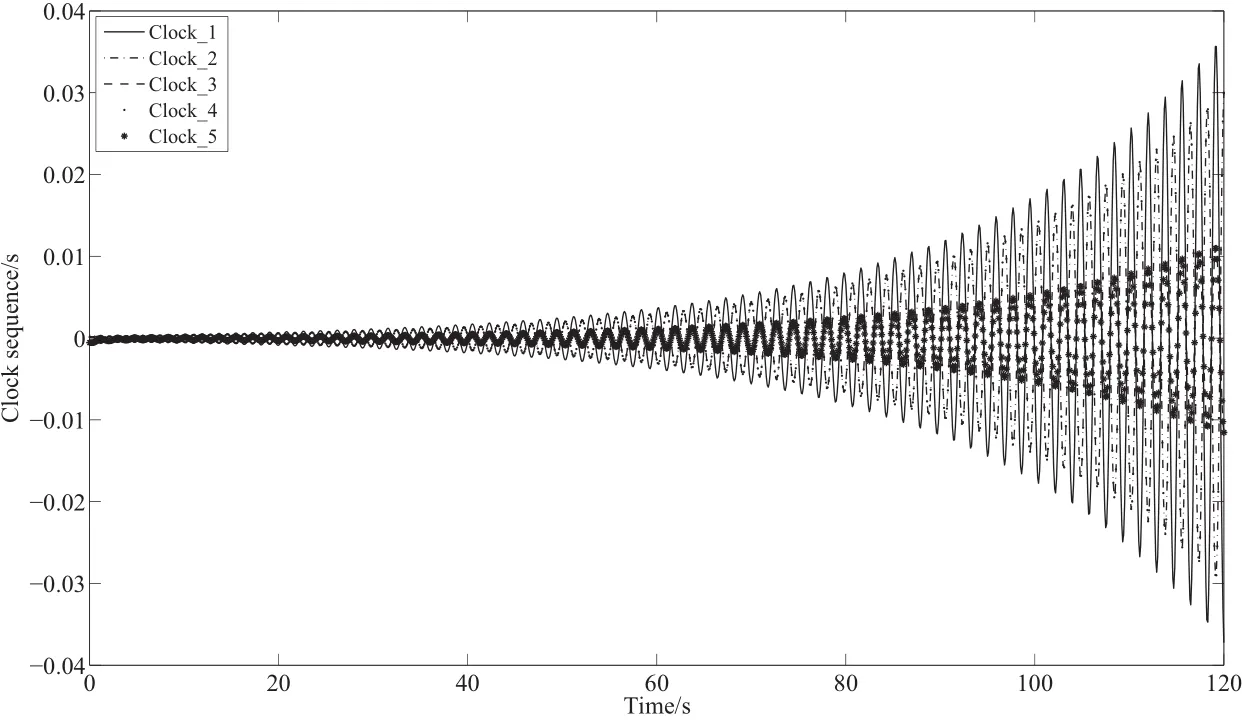
图17 τ=0.45 s时的单时延群体系统时钟观测序列Fig.17 T he clock sequence of the netw ork system with one tim e delay forτ=0.45 s

图18 τ=0.45 s时的单时延群体系统的钟速观测序列Fig.18 T he clock rate sequence of the netw ork system with one tim e delay forτ=0.45 s

4 结论

时间同步在飞行器编队以及星座自主导航等方面具有重要作用.在此应用中,在某给定时刻,每个观测节点之间未必互联互通,即该节点只能观测或者获取相应邻居的时间信息.因此,研究如何在网络节点只获得邻居局部信息的情况下,实现网络系统的时间同步是非常重要的.针对这一问题,提出了一种分布式系统中时间同步的新方法.将每个时钟看作网络系统中的节点,首先定义了不同的分布式系统拓扑结构,在此基础上,定义和设计了相应的时钟同步控制算法.分别设计了无主钟(参考时钟)、有主钟(参考时钟)和网络系统中存在固定通信时延的时钟同步方法.通过稳定理论分析和仿真实验验证了所设计时钟同步协议的正确性.

参考文献

[1]王正明.天文学进展,2004,22:104

[2]赵书红,王正明,尹东山.天文学报,2014,55:313

[3]Zhao S H,W ang Z M,Y in D S.ChA&A,2015,39:118

[4]李变,屈俐俐,高玉平,等.天文学报,2010,51:404

[5]Li B,Qu L L,G ao Y P,et a l.ChA&A,2011,35:209

[6]方琳,杨旭海,孙保琪,等.天文学报,2013,54:355

[7]雷雨,赵丹宁.天文学报,2014,55:216

[8]席超,蔡成林,李思敏,等.天文学报,2014,55:78

[9]X i C,Cai C L,Li S M,et a l.ChA&A,2014,38:342

[10]Bo lognan i S,Carli R,Lov isari E,et a l.A Random ized Linear A lgorithm for C lock Synch ron ization in M u lti-Agent System s.Decision and Control 51st Annual Con ference on IEEE,2012:20

[11]Takaba K.Synchron ization of Linear Agents with Sector-bounded Input Non linearities.Control,Autom ation and System s 15th In ternationa l Con ference on IEEE,2015:1

[12]Li Z K,Duan Z S,Chen G,et al.Circu its and System s I:Regu lar Papers,IEEE Transactions,2010, 57:213

A Novel M ethod of C lock Synch ronization in D istribu ted System

LIGun NIU Meng-jie CHAIYang-shun CHEN Xin REN Yan-qiu

(Schoo l of Aeronau tics and A stronau tics,Un iversity of E lectron ic Scien ce and Technology of China, Chengdu 611731)

Time synchronization p lays an important role in app lication of aircraft flying formation and constellation autonomous navigation,etc.In application of clock synchronization in the network system,it is not always true that each observed node may be interconnected,therefore,it is difficult to achieve time synchronization of network system with high precision in the condition that a certain node can only obtain the measurement information of clock from one of its corresponding neighbors,and cannot obtain from other nodes.According to this special problem,a novelmethod of high precision time synchronization of network system has been proposed.In this paper,we regard each clock as a node in the network system,and based on different distributed topology definition,the follow ing three control algorithm s of time synchronization under three circum stances have been designed:without amaster clock(reference clock), with a master clock(reference clock),and with a fixed communication delay in the network system.The validity of the designed clock synchronization protocol has been proved both theoretically and through numerical simulation.

astrometry:time,methods:data analysis

P127;

A

10.15940/j.cnki.0001-5245.2016.02.007

2015-09-16收到原稿,2015-11-16收到修改稿

∗国家863基金项目(2014XXX5431)资助

†ligun@uestc.edu.cn