SS 433的周期性X射线光变研究∗

王俊义 陆相龙 赵秋雯 董典桥 劳保强 陆扬 魏延恒 伍筱聪 安涛

(1桂林电子科技大学广西信息科学实验中心 桂林 541004) (2桂林电子科技大学广西密码学与信息安全重点实验室 桂林 541004) (3中国科学院上海天文台 上海 200030)

SS 433的周期性X射线光变研究∗

王俊义1,2†陆相龙1,2,3赵秋雯3董典桥1,2,3劳保强3陆扬3魏延恒3伍筱聪3安涛3

(1桂林电子科技大学广西信息科学实验中心 桂林 541004) (2桂林电子科技大学广西密码学与信息安全重点实验室 桂林 541004) (3中国科学院上海天文台 上海 200030)

SS 433是目前为止唯一一个被同时检测到轨道周期、超轨道周期和章动周期且存在双向螺旋状喷流的X射线双星系统,通过研究它的X射线光变将有助于理解系统的动力学过程及与其他波段的相关性.利用Lomb-Scargle周期图法(简称LS周期图)和加权小波Z变换法(Weighted W avelet Z-transform,WW Z)对SS 433的Sw ift/BAT(Burst A lert Telescope)(15–50 keV)和RXTE/ASM(Rossi X-Ray T im ing Explorer/A ll-Sky M onitor)(1.5–3,3–5和5–12 keV)光变曲线进行周期提取,并对得到的周期成分进行蒙特卡洛仿真.其中15–50 keV能段:检测到5个较强的周期成分P1(～6.29 d)、P2(～6.54 d)、P3(～13.08 d)、P4(～81.50 d)和P5(～162.30 d);3–5和5–12 keV能段:都检测到P3(～13 d)和P5(～162 d)的周期成分;1.5–3 keV能段:未检测到任何明显的周期存在.3–5、5–12和15–50 keV能段的功率谱上最强的周期信号均为P5,且P5与之前对光学光变曲线研究得到的结果一致,结合SS 433的螺旋形射电喷流,推测周期为～162 d的X射线和光学波段光变与相对论性喷流的进动有关,X射线与光学光变周期的一致性也表明两个波段的辐射机制有内秉联系.P3与之前研究中检测到的系统轨道周期(～13.07 d)一致,P2和P4则分别为P3和P5的一个高频谐波成分.P1成分仅在15–50 keV能段的功率谱中被检测到,且它与系统的章动周期一致.随着能段能量的降低(硬X射线到软X射线),所检测到的周期成分却越来越少,这一结果很好地印证了高能段(硬X射线)辐射主要来自于喷流,低能段(软X射线)辐射则可能是由双星系统周围的介质主导.通过分析得到的多个X射线光变周期,为今后SS 433的多波数据分析、系统的动力学机制等研究提供有力的参考依据.

恒星:双星,周期,方法:小波变换,Lomb-Scargle周期图法,自回归过程

1 引言

光变指的是天体辐射流量随时间的变化,光变分析是研究天体辐射机制和内部结构及其变化的常用手段.尤其是遥远致密天体无法通过直接成像的方法获得内部能源的动力学信息,光变分析就显得尤为重要.通过对天体光变的时间序列分析可以得到许多有用的物理参数,例如光变周期、光变幅度、相位、不同波段光变之间的相关性和时间延迟等.这些物理参数对揭示光变现象背后的物理机制很有帮助,同时也可以用来对未来光变趋势进行预测.具体来说,通过对某一特定天体的光变曲线进行记录和时间序列分析,可以寻找和证认该天体光度的特征变化周期,从而对下次“爆发”的时间进行推断,并进行有针对性地组织观测.除此之外,还可通过观测得到的周期来估算天体的质量等物理参数,或发掘驱动周期性光变的物理机制.类似的光变研究已经广泛地用于X射线双星[1–3]和超大质量黑洞[4-5]的研究中.

SS 433位于超新星残骸W 50中心,是一个中心致密天体为中子星或黑洞、伴星为1颗晚期A型星[6-7]的X射线双星系统[8].它在Stephenson和Sanduleak命名的强射电源星表中排在第433个,加上两人名字的首字母均为S,因而得名SS 433.从1978年SS 433被发现以来,对它非凡特性的研究就成为了天体物理学中的一个关注热点[9–12].首先,它是第1颗被发现有相对论性射电喷流的银河系内天体[13],是研究喷流物理的模板,同时又是第1颗被发现的微类星体.它两端喷流的速度高达～0.26c(c为光速),并以～162 d的周期,沿半张角为20°的圆锥进动,外型上呈现出螺旋状[14].此外,喷流的质量亏损率＞5×10−7M⊙·yr−1,动力学光度Lk＞1039erg·s−1[14-15].除了喷流之外,它还具有强烈的外流,速度高达～1500 km·s−1,这很可能会影响W 50周围的星云[14].此外,SS 433存在多波段的光变(可见光、无线电波和X射线),射电强度和X射线强度还经常发生剧烈变化.早期人们通过谱线观测得到了它的章动周期(～6.29 d)[16],轨道周期(～13.08 d)[17]和进动周期(～162 d)[11].1986年, Kem p等人对SS 433长达6 yr(1979–1985)的光学V波段数据进行分析,得到了6.54 d、13.08 d和162 d的周期成分,跟早期谱线得到的结果一致[18].2006年,Wen等人使用RXTE/ASM(Rossi X-Ray Tim ing Explorer/All-Sky Monitor)中SS 433的X射线光变数据(时间跨度约为8.5 yr)进行处理,同样检测到了13.1 d和162 d的周期成分[19],但并没有检测到约6 d的章动周期.本文将基于Swift/BAT(Burst A lert Telescope)(15–50 keV)和RXTE/ASM(1.5–3,3–5和5–12 keV)的X射线数据[20]对SS 433进行周期分析.到目前为止,Swift观测总时间长达10 yr(有天平均数据和单轨道数据),而且数据的采样间隔短(≥1 d),RXTE/ASM的观测数据长达15 yr(有天平均数据和94 s数据),涵盖4个能段(1.5–3,3–5,5–12和1.5–12 keV).这些数据却有助于搜寻长时标(几十天)和短时标(几天)的周期信号.图1为SS 433的RXTE/ASM和Swift/BAT光变曲线,其中X轴是用修正儒略日(M odified Julian Day,M JD)表示的观测时间.图1(a)、(b)和(c)为SS 433的RXTE/ASM天平均数据(剔除了误差大于1 cts·s−1的数据点),时间范围从1996年1月6日(M JD 50088)到2011年10月12日(M JD 55847),跨度为5 759 d(约15.8 yr),其中包含3个波段数据:1.5–3 keV(图1(a)),3–5 keV(图1(b)),5–12 keV(图1 (c)).图1(d)为SS 433的Swift/BAT天平均数据(剔除了误差大于0.01 cts·cm−2·s−1的数据点),时间范围从2005年2月14日(M JD 53415)到2015年4月2日(M JD 57114),时间跨度为3 699 d(～10.1 yr).

图1 SS 433的RXTE/ASM(图(a)、(b)和(c))和Sw ift/BAT(图(d))光变曲线Fig.1 The RXTE/ASM(panels(a),(b),and(c))and Sw ift/BAT(panel(d))ligh t cu rves of SS 433

另一方面,传统的信号处理技术大多是针对均匀采样信号和基于离散傅里叶变换的,即通过频域傅里叶变换分析来描述信号的功率谱特征.然而在许多实际的应用场合中,所观测、采集的时间序列数据的采样间隔往往是不均匀的,比如,在空间望远镜对天体的流量密度监测的过程中,由于地球对目标源的遮挡、南大西洋异常区(SAA区)设备关闭,以及设备在空间运动过程中所覆盖不同的天区等因素的影响,造成了观测到的光变曲线经常是非均匀采样.传统的傅里叶变换分析方法在处理连续、均匀采样的时间序列时能够得到很好的频谱图,但当处理不均匀采样且包含有大量噪声的实际观测数据时,时间序列的非均匀性和有限时间跨度等因素会在傅里叶变换的功率谱中引入较多噪声,并产生虚假谱峰以及特征谱的能量泄露等[21].如果噪声过大,真实周期信号成分的振幅和相位也会产生很大的误差,严重的情况下将会导致参数提取错误或者周期证认失败.另一方面,如果周期信号不稳定,即随着时间演化而变化,那么也会很大程度上影响傅里叶分析的结果.因此,为了能够准确可靠地提取出非均匀时间序列信号中的重要特征参数信息,非常有必要使用一些动态功率谱分析方法[22].

文章结构安排如下:第2节分别介绍了基于时域分析的Lomb-Scargle周期图法、用以检测周期成分是否由红噪声影响而产生的一阶自回归过程和基于小波变换(时-频分析)的加权小波Z变换法.第3节将上述3种算法应用于SS 433的Swift/BAT(15–50 keV)和RXTE/ASM(1.5–3,3–5和5–12 keV)天平均数据中进行周期提取和置信度分析,并结合检测到的周期对各光变曲线进行折叠.最后对各个周期成分进行分析和总结.

2 算法原理

2.1 Lom b-Scargle周期图法

观测采集的光变曲线数据在时间域上是离散分布的,即离散时间序列可表示为x(tn),tn表示第n时刻.对于均匀采样的离散时间序列x(tn),其频谱对应的离散傅里叶变换(DFT)为:

其中N为序列的总数据点数,f为测试频率.

对于非均匀采样时间序列的功率谱分析,最常采用的方法是Lomb-Scargle周期图法[21,23].LS周期图法基于离散傅里叶变换原理,把时间序列分解为一系列正(余)弦函数的线性组合y=a cosωt+b sinωt,并在此基础上,将信号特征从时域转换到频域上.LS周期图法通过对数据用模型曲线(正弦函数)进行最小二乘法拟合,利用均方根误差来判断数据隐含的周期变化趋势和猜想模型的符合度,如此使得傅里叶技术可以等同地应用在非均匀采样信号上,不仅能有效地从时间序列中提取出弱周期信号,还能在一定程度上减弱时间序列不均匀性所产生的虚假信号.对于非均匀采样时间序列x(ti),i=1,2,3,···,N,LS周期图的功率谱定义为:

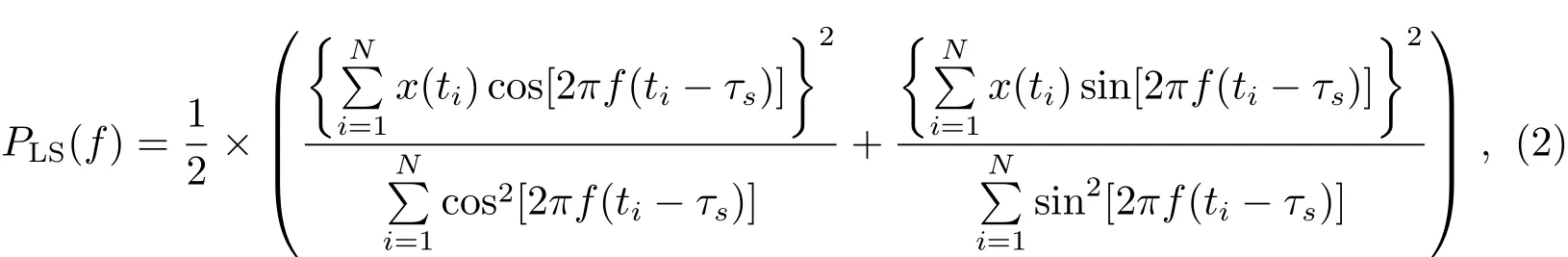
其中τs为时间偏移量.τs的定义为:

其中ω=2πf.实践证明,对于正弦型、无较大间断的时间序列进行周期分析时,LS周期图算法可以达到最佳的处理效果;当时间序列背后隐藏的物理过程无法用三角函数形式拟合或者存在不均匀的大间断的情况时,LS周期图对频率和幅度的估算会出现较大的误差,做出的周期判断往往不是最可靠的.

随机噪声往往会影响周期提取算法对时间序列的分析,进而造成检测结果的不确定性.在天文学、气象学和地理学的数据中,这些随机噪声一般是由随机过程产生的,并且它们的功率谱服从幂律分布,即P～f−α.当α=0时,随机噪声呈现出白噪声的特性,并在功率谱的高频段产生一系列虚假的峰;当1＜α≤2时,随机噪声则会呈现出红噪声的性质,进而在低频段的功率谱占主导地位.

1976年,Hasselmann[24]指出:一阶自回归过程(First-order Autoregressive,AR(1))可以很好地描述红噪声的特性,其数学表达式为:

其中,ε(ti)是均值为0、方差为固定值的白噪声.

一阶自回归模型是一种线性预测模型,即已知N点数据,则可根据模型推出第N点前面或者后面的数据,其本质上类似于插值计算,目的都是为了增加有效数据点.二者的不同点在于一阶自回归模型是一个N点递推模型,而插值计算过程是由邻近几点通过某种计算得到插值数据,所以一阶自回归模型相比插值计算方法推断效果好.

此外,AR(1)模型常被当做一种空假设(null hypothesis),用来检验一个时间序列是否具有某种随机的特性,例如判断一个时间序列是否是红噪声序列.如果时间序列是均匀采样的,则上述红噪声检测过程是较为成熟的.当时间序列是非均匀采样时,往往先通过插值处理将非均匀时间序列转变为一个均匀采样的信号,当然这样处理的一个问题是会导致时间序列的“失真”,甚至导致时间序列频谱相对于真实频谱出现“过红”的现象.

Robinson[25]对原先的AR(1)过程进行改进,于1977年提出了一种能处理非均匀采样序列的AR(1)过程.主要的改进在于,原来的AR(1)中的白噪声是一个跟时间不相关的白噪声过程,而在这里是依赖于时间的;原来的序列去掉白噪声部分是有固定的关系,而在这里是一个依赖时间的变化的量.非均匀采样序列的AR(1)过程定义为:

其中ε(ti)是均值为0、方差σ2ε≡1−exp(−2(ti−ti−1)/τ)的高斯白噪声.ρi=exp(−(ti−ti−1)/τ),τ为AR(1)过程的特征时间尺度(也叫持续时间).Mudelsee[26]指出可以使用最小二乘法对其进行估计.

AR(1)过程的功率谱密度为:

其中fNyq为奈奎斯特频率,G0为平均频谱幅度,ρ为平均自相关参数.ρ是使用采样间隔的算术平均得到的,即ρ=exp(−Δt/τ),其中Δt=(tN−t1)/(N−1).

为了能将红噪声检测与先前提到的LS算法相结合,Schu lz和Stattegger将WOSA (Welch overlapped segment averaging)技术与LS算法相结合,即将时间序列X(ti)分为n50个部分,每个部分有50%的数据是相互重叠的,对这些分段数据求平均,得到平均周期谱.然而,由于LS算法的固有缺陷,即总是过高地估计了信号的高频成分,如果直接对第2.1节中LS的频谱进行红噪声检测,那是“偏颇”的.为此,Schulz对LS的频谱进行修正,具体步骤如下:(1)使用文献[26]中提到的时域算法从X(ti)中估计出τ值.大致方法如下:Mudelsee将exp(−1/τ)定义为a,即a=exp(−1/τ).代入AR(1)过程为:

从上式中可以看出a的值介于0和1之间.使用Brent的方法[26−27]求得ˆa,使得下式最小化:

2.2 加权小波Z变换

2.2.1 小波变换

小波(wavelet),顾名思义,即一个小范围区域的波,是一种特殊的、长度有限的、平均值为零的波形.它有两个特点:一是“小”,即具有衰减性;二是具有正负交替的“波动性”,即直流分量为零.小波分析是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,能自动适应时频信号分析的要求,可聚焦到信号的任意细节.在小波分析中,信号被分解成一系列小波函数,而这些小波函数都是由一个母小波函数经过平移与尺度伸缩得到的.正是由于小波在时间和频率域的局域性特征,用这种不规则的小波函数可以逼近那些非稳态信号中尖锐变化的部分,也可以去逼近离散不连续具有局部特性的信号,从而更为全面地反映原信号在某一时间尺度上的变化.

其中,w(a,τ)称为小波变换系数,而函数族Ψa,τ(t)是由某种特定的窗函数经过尺度变换和平移变换生成,可以将其表示为:

其中a为尺度因子,τ为时移因子,Ψ(t)是某种特定类型的窗函数,将其称为母小波, |a|−1/2为归一化常数,用来确保小波内积为1.需要注意的是,小波变换所采用的母小波既可以是复数信号又可以是实数信号.此外,母小波也必须符合下列公式:

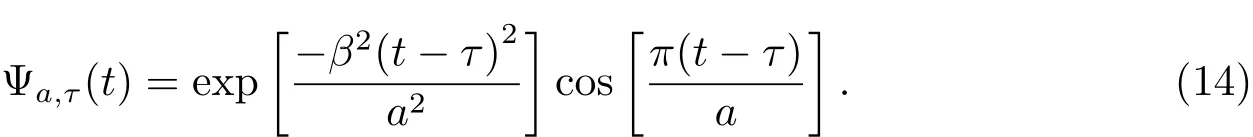
很明显,莫莱小波本质上是一个幅度随着时间演化衰减至0的余弦函数,特别要注意的是小波函数里多了一个参数β.此参数控制了小波的形状,同时也影响莫莱小波转换在时间轴与频率轴上的分辨率.当β为0时,莫莱小波有最佳的频率分辨率,随着β值上升,频率的分辨率下降,时间轴的分辨率上升,到达无限大时,拥有最佳的时间分辨率.

图2 M orlet小波函数Fig.2 The M orlet w avelet

我们以莫莱小波为小波基对时间序列进行连续小波变化,从中寻找周期.首先将时间序列从时域映射至时频域中,然后在映射得到的时频图中识别得到时间序列的特征周期.但是,对于非均匀采样间隔的时间序列,实际应用中发现使用连续小波变换对其进行分析所得到的处理结果往往并不是十分理想.正如Foster[28]指出的,小波变换对于时间序列的采样间隔十分敏感,很多时候无法直接利用小波分析方法找到时间序列的真实周期.为解决这一难题,Foster提出一种加权小波Z变换算法,该算法基于小波变换原理,可以直接对非均匀采样时间序列的周期进行检测[29].

2.2.2 加权小波Z变换算法

如Foster[28]所述,将M orlet小波作为母小波,经过平移、伸缩后得到:

使用莫莱小波对信号进行变换时,可以将小波函数f(z)理解为2部分:第1部分为基函数eiω(t−τ),代表平面波;第2部分为一个加权项e−cω2(tα−τ)2,表征了1个高斯型轮廓. Foster使用了3个测试函数[29],分别记为:

并在映射时加入统计加权项e−cω2(tα−τ)2.同时定义有效数目Neff表示局部采样点:

Foster[28]将两函数f(t)和g(t)的内积定义为:

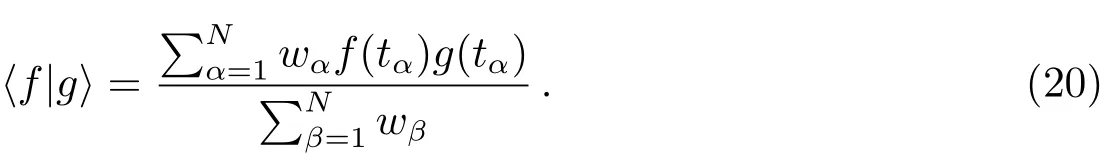
则将以上各式代入Foster[28]提出的通用统计能量(Universal Power Statistic,UPS):

其中,1表示常数向量[1,1,1,···,1],s2为数据的估计方差,Si,j为φi与φj的内积〈φi|φj〉, P满足自由度为r−1的卡方分布,且期望值为1.进而得到加权小波变换(Weighted Wavelet Transform,WW T):

其中,Vx和Vy分别为数据和模式函数的加权方差:

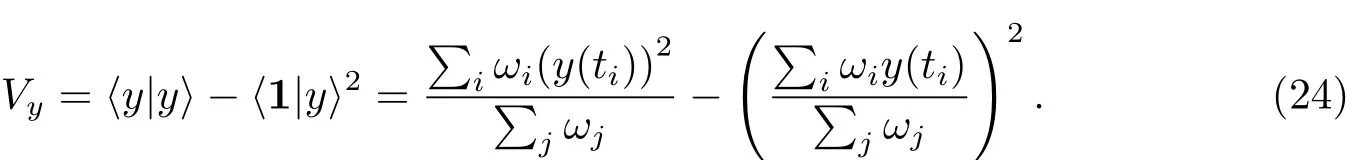
在信号的较低频率,由于窗口比较宽,更多的数据点被作为采样点,导致WWT峰值偏向较低的频率,为了解决这个问题,对WWT重新定义.定义Z变换的小波变换为:

其中,WW Z满足自由度为Neff−3和2的F分布[29].

WW Z与LS相比有很多优点,比如时频域同时分析、多分辨率的周期分析,而且得到的结果更具有统计意义(在计算过程中引入了统计量),满足统计F分布.缺点是WW Z涉及到的计算量更大、映射变换更复杂,算法的运算耗时较长,产生的数据量也较大,但是这些缺陷随着计算机处理能力的提高已经不再是首要制约因素了.

3 周期分析结果

用LS算法结合红噪声检测方法对SS 433的RXTE/ASM和Swift/BAT数据进行周期检测和置信度分析,检测范围从5 d到300 d,结果如图3所示,其中图3(a),图3(b),图3(c)和图3(d)分别对应于Swift/BAT(15–50 keV)和RXTE/ASM 3个能段(1.5–3,3–5和5–12 keV)数据的处理结果.图中实线代表修正后的LS周期图,点划线代表从1 000次蒙特卡洛仿真中得到的99.74%(3σ)的统计置信度曲线(错误警戒线[30]),虚线代表理论红噪声功率谱.横轴表示测试频率(单位为d−1),纵轴表示功率谱密度,图像中的尖峰对应可能的特征周期.图3(a)中,峰值较大的周期成分总共有5个(已用箭头在图中标注),对应的周期分别为P1=6.29±0.01 d(f1=15.90×10−2d−1,峰值为1.57×10−4)、P2=6.54±0.01 d(f2=15.29×10−2d−1,峰值为1.86×10−4)、P3=13.08±0.02 d(f3= 7.64×10−2d−1,峰值为2.59×10−4)、P4=81.50±0.53 d(f4=1.23×10−2d−1,峰值为2.39×10−4)和P5=162.28±2.52 d(f5=0.62×10−2d−1,峰值为16.77×10−4).其中峰值最强的周期成分为P5,峰值约为次峰P3的6.5倍.P5和P3正好分别是P4和P2的两倍,即P5≈P4×2,P3≈P2×2.此外,P5成分的置信度远远高于3σ的警戒线,P1,P2, P3和P4也都略高于3σ的警戒线.在图3(b)和3(c)中,分别有一处明显高于3σ的警戒线的周期成分,即P5=163.64±3.88 d(f5=0.62×10−2d−1,峰值为15.69)和P5=162.71±5.55 d(f5=0.61×10−2d−1,峰值为4.82).而对于图3(d),我们并没有看到存在明显的周期成分.

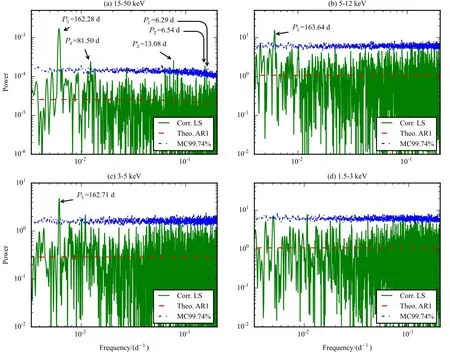
图3 SS 433 Sw ift/BAT和RXTE/ASM数据的LS周期图和红噪声功率谱.(a)15–50 keV;(b)5–12 keV;(c) 3–5 keV;(d)1.5–3 keVFig.3 T he LS p eriodogram s and red noise spectra of Sw ift/BAT and RXTE/ASM ligh t cu rves of SS 433.(a)15–50 keV;(b)5–12 keV;(c)3–5 keV;(d)1.5–3 keV

对于WW Z算法,使用较小的衰减因子c能提高频率上的解析度,但缺点是会模糊信号在时域上的变化趋势,反之亦然.为了能很好地呈现出各个周期成分的趋势特性,在使用WW Z算法对SS 433进行处理的过程中,分别使用了不同的衰减因子c.最终结果如图4中所示,其中图4(a),4(b)和4(c)分别对应于的周期检测范围为50–300,12.5–13.5和6.2–6.7 d的Swift/BAT 15–50 keV能段数据的WWZ功率谱,图4(d),4(e)和4(f)分别为RXTE/ASM 5–12,3–5和1.5–3 keV能段数据的WWZ功率谱(周期检测范围均为100–220 d),图4(g),4(h)和4(i)则分别为RXTE/ASM 5–12,3–5和1.5–3 keV能段数据的WW Z功率谱,只是周期检测范围为12.5–13.5 d.WWZ的功率谱图为一个三维等高值图,横坐标X代表SS 433的观测时间(M JD),纵坐标Y代表检测的周期(单位为d),Z坐标代表各点的功率值.功率值越高,则该点是周期成分的可能性越大,随着时间轴(X轴)的变化,周期值的变化一方面反映了真实的物理过程,另一方面是受光变数据(采样间隔等)影响的结果.此外,为了方便与之前的LS算法结果作比较,在WWZ的功率谱图像的左边附上了LS算法的功率谱,其中它们使用相同的Y坐标轴.

图4 SS 433 Sw ift/BAT和RXTE/ASM数据的WW Z功率谱Fig.4 The WW Z pow er spectra of Sw ift/BAT and RXTE/ASM ligh t cu rves of SS 433

从图4(a)的WW Z功率谱中很容易识别出最明显、幅度最高的P5(168.63±5.61 d)成分,它在时-频域上的走势已用白色虚线进行标注,很高功率值也反映该周期成分在光变曲线中很明显.该成分除了在开始的300 d时间段内比较弱外(这主要是由于该处对应的光变曲线存在缺失造成的),在整个观测时间范围内都很持续且稳定.此外,P4成分主要出现在M JD 55000之后,虽然不是很稳定,但仍然可以区分3个主要部分(已用白色虚线标出),它们的范围为:M JD 55083–55576,M JD 55537–56330和M JD 56649–57114,且周期为(79.41±0.71)d.而且它的大体形状和P5成分的形状很类似,数值还为P5成分的一半左右,即P5≈P4×2,很有可能为P5成分的一个谐波分量,这种情况在基于傅里叶变换的方法中非常常见.图4(b)中已经用白色虚线标注了P3周期成分,在整个观测时间范围内,P3成分都比较稳定且贯穿整个观测时间,并在M JD～56548时,功率值达到峰值点14.45,该功率谱很好地反映了该成分在整个观测数据内都一直存在且很稳定.图4(c)的WW Z功率谱中P1和P2成分也十分明显,其中P1成分最为稳定,周期值保持在(6.28±0.01)d,但在M JD～56100时,该周期成分开始变弱并最终消失; P2成分从M JD～54343时开始出现,并在之后的时间范围内有所波动,但周期值都保持在(6.54±0.01)d,并且功率值在M JD 56403处达到峰值8.76.图4(d)和4(e)中我们都能看到P5周期成分的存在,大致趋势如白色虚线所示.然而该周期成分并没有如图4(a)中的如此持续,而是存在不同程度的波动,在M JD 55000之后更是消失了,消失的原因主要是光变数据在M JD 55000附近的缺失.在图4(f)中,弥散的功率谱表明该检测范围内没有明显的周期成分存在.在图4(g)和4(h)中我们都能看到约13.08 d周期成分(P3)的存在,范围分别为M JD 50500-54500和M JD 51000-54500.虽然周期比较稳定,但不够持续,即在观测初期和末期消失了,这主要是由于在这两段时间内周期本身就不明显.而在图4(i)中,功率谱也相对弥散,这表明该检测范围内不存在明显的周期.

此外,我们根据LS算法得到的周期结果对相应光变曲线进行折叠,结果如图5所示.图5(a),5(b)和5(c)分别为使用Swift/BAT 15–50 keV能段数据按照P5=162.28 d, P3=13.08 d,P1=6.29 d周期进行折叠得到的折叠曲线.在图5(a)中我们可以看出在一个相位周期内脉冲的形状和强度.图5(d)和5(e)分别为使用RXTE/ASM 5–12和3–5 keV能段数据按照P5=163.64 d和P5=162.71 d进行折叠得到的折叠曲线,也得到了类似上述的结果.在之前的算法处理结果中,我们并没有在RXTE/ASM 1.5–3 keV能段数据中检测到P5周期成分,但为了进一步进行验证,我们对该数据按照162 d的周期进行折叠,结果如图5(f)所示.此外,我们将RXTE/ASM 3个能段的数据按照轨道周期P3=13.08 d进行折叠,结果如图5(g),5(h)和5(i)所示,从高能到低能的折叠曲线呈现出一个逐渐混乱(不规则)的过程.

图5 SS 433 Sw ift/BAT和RXTE/ASM数据的折叠曲线Fig.5 The fo lded ligh t cu rves of Sw ift/BAT and RXTE/ASM light cu rves of SS 433

4 总结

本文首先使用LS周期图法对SS 433的X射线光变曲线进行初步的周期提取,然后利用一阶自回归过程模拟光变数据的红噪声,并通过蒙特卡洛仿真对检测到的周期进行置信度统计,最后运用WW Z算法对LS算法中得到的周期成分的时间变化特征进行了分析,并使用等高值图呈现出每个周期成分在时-频域上的分布和走势(结果如表1所示).本文的主要结论如下:

(1)P3:在4个能段数据的周期检测结果中,LS算法只在15–50 keV能段数据中检测到了～13.08 d周期(P3)的存在(图3(a)).该成分的统计置信度明显高于3σ警戒线,这可以说明它由随机噪声造成的可能性很小.此外,该结果对应于Kem p等[18]通过光学波段得到的约13.08 d轨道周期,因此判定该周期为SS 433的轨道周期成分.虽然Wen等[19]只在8.5 yr的RXTE/ASM 5–12 keV能段数据中检测到了(13.090±0.001) d的轨道周期,但在我们使用WW Z算法处理约15 yr的RXTE/ASM 3个能段数据得到的结果中(图4(g),4(h)和4(i)),3–5和5–12 keV能段都存在约13 d的周期,尽管功率不是很强.在4个能段数据按照轨道周期(P3=13.08 d)折叠得到的折叠曲线(图5(b), 5(g),5(h)和5(i))中,15–50,5–12和3–5 keV数据的折叠曲线与Cherepashchuk等[31]使用INTEGRAL(INTErnationalGamma Ray Astrophysics Laboratory)数据得到的结果极为相似,且形状也类似于交食状的光变曲线.Cherepashchuk等[31]认为这个类交食状的X射线能量衰减是由于X射线发射区域受到周期性的遮挡造成的.在4个折叠曲线图中(图5(b),5(g),5(h)和5(i)),随着能段的降低,这个类似于交食现象也越来越不明显;

表1 SS 433周期检测结果Tab le 1 T he p eriod-d etected resu lts of SS 433

(2)P5:在4个能段数据的周期检测结果中,LS算法和WW Z算法在15–50,5–12和3–5 keV能段数据中都检测到了约162 d的周期成分.该成分一方面具有超高置信度(远远高于3σ警戒线),另一方面它与M argon等[12](率先发现SS 433的发射谱线中红移值和蓝移值随着时间有(164±4)d的周期性漂移)和Kem p等[18](通过光学波段得到的～162 d周期)的研究结果一致.此外,X射线波段与可见光波段结果的吻合,以及射电波段观测到螺旋进动喷流也进一步证实了SS 433的X射线光变与其相对论性喷流的进动相关.3者的折叠曲线(图5(a),5(d)和5(e))中也很好地展示了一个相位周期内的流量变化;

(3)P1:早在1981年,Newsom和Collins首先宣布发现了SS 433的“运动”谱线的波长具有～6 d的短周期变化,但结果却备受怀疑[16].随着其他天文团队纷纷证实该短周期的存在,才使得这个结果逐渐被世人认可,并最终成为了SS 433的又一重要特性.此外,该成分在SS 433的光学波段[18]和射电波段[32]数据中也都有检测到,且被认为是系统的章动周期.在本文4个能段数据的周期检测结果中,LS算法和WW Z算法只有在15–50 keV能段数据中检测到了章动周期的存在.这也再次印证了X射线、光学和射电光变之间存在内在相关性;从相应的折叠曲线(图5(c))可以看出,其形状类似于正弦型;

(4)P2和P4:在第3节的检测结果中,～6.55 d(P2)和～81.50 d(P4)周期的统计置信度超过了3σ警戒线,且分别与P3和P5存在2倍的关系,即P5≈P4×2,P3≈P2×2.此外,在WW Z功率谱图中,P2和P4有随时间变化趋势的迹象,特别是P2和P3具有明显相似的随时间变化走势,很好地印证了两者之间的谐波关系.谐波成分在以往的周期分析中并不少见,例如在文献[33]中,多个样本都存在谐波成分.在之前的SS 433检测中,6.55 d(13 d周期的谐波成分)的周期也都有被检测到[31].据此推断P2和P4分别为P3和P5的一个高频谐波成分.

本文在对SS 433的4个X射线能段(Swift/BAT 15–50 keV,RXTE/ASM 5–12,3–5和1.5–3 keV)的光变分析中检测到了多个周期成分的存在,特别是在15–50 keV能段数据中同时检测到章动周期(P1)、轨道周期(P3)和进动周期(P5),这在目前已知的双星系统中并不多见,仅有Her X-1和SS 433[34].类似的多周期现象也存在于活动星系核中,比如,Katz[35]等检测到OJ287存在多个周期信号,并推测其中1.2 yr周期是由章动引起的.

另一方面,图4(a),4(d)和4(e)的WWZ功率谱很好地证实了:～162 d的进动周期(超轨道周期)是长期稳定存在的.超轨道周期在近些年来已屡见不鲜,在很多X射线双星的X射线和可见光波段都有被观测到,但像SS 433中～162 d的长期稳定存在的超轨道周期实属少见.超轨道周期产生的原因有:吸积盘进动、相对论喷流的进动、磁场扭曲等.但大多数情况下,后两种物理机制产生的超轨道周期都是不稳定和不持续的.Kotze等人指出只有扭曲的吸积盘或者相对论性喷流进动能产生稳定的进动,进而在光变曲线上产生超轨道周期信号(例如:Her X-1和LMC X-4).SS 433的～162 d周期就很有可能是由于相对论性喷流的进动产生的[8].至于喷流的进动机制,一般认为是盘致进动或者黑洞自身导致的.对于SS 433,目前普遍接受的是盘致进动导致喷流的进动.Begelman等[36]认为:起初,吸积盘和喷流的轴心是一致的,但由于受到某种外力的作用,吸积盘开始发生进动,而此时喷流则仍垂直于原始的吸积盘面.由于SS 433超高的质量转换率,其外流异常剧烈,速度高达～1500 km·s−1[36].这也使得外流与喷流不断发生相互作用,最终导致吸积盘与喷流轴心相结合且同步进动.同样地,～6.29 d的章动周期也是通过这种方式传导到喷流上,并最终被观测到.章动和进动从吸积盘到喷流的传递,为在恒星级质量黑洞系统中研究吸积盘和喷流的耦合提供了有力的证据.

随着能段能量的降低(硬X射线到软X射线),检测到的周期数越来越少,即:在15–50 keV能段检测到章动周期、轨道周期和进动周期,在5–12和3–5 keV能段检测到轨道周期和进动周期,在1.5–3 keV能段未检测到任何周期,这也很好地印证了高能段(硬)X射线辐射主要来自于喷流,低能段(软)X射线辐射则可能主要来自于双星系统周围的介质,因此软X射线辐射一般没有明确的周期特征.

[1]Rem illard R A,M cC lintock J E.arX iv p rep rin t astro-ph/0606352

[2]董爱军,盖宁,张福安.天文学报,2012,53:391

[3]Dong A J,G ai N,Zhang F A.ChA&A,2013,37:139

[4]M eyer L,Eckart A,Schodel R,et a l.A&A,2006,460:15

[5]Gonzalez-M artin O,Vaughan S.A&A,2012,544:80

[6]K und t W.A p&SS,1987,134:407

[7]K und t W.Jets from Stars and G a lactic Nuclei.Berlin:Sp ringer,1996:471

[8]Kotze M M,Charles P A.M NRAS,2012,420:1575

[9]Fabian A C,Rees M J.M NRAS,1979,187:13

[10]M ilgrom M.A&A,1979,78:9

[11]Abell G O,M argon B.Natu re,1979,279:701

[12]M argon B,G rand i S A,Stone R P S,et al.Ap J,1979,233:63

[13]Davidson K,M cC ray R.Ap J,1980,241:1082

[14]Begelm an M C,K ing A R,P ring le J E.M NRAS,2006,370:399

[15]B rinkm ann W,K aw ai N.A&A,2000,363:640

[16]New som G H,Co llins G W.A p J,1981,86:1250

[17]C ram p ton D,Cow ley A P,Hu tch ings J B,et a l.IAU C irc,1979,3388:1

[18]K em p J C,Henson G D,K raus D J,et a l.A p J,1986,305:805

[19]W en L,Lev ine A M,Corbet R H D,et a l.A p JS,2006,163:372

[20]K rimm H A,Ho lland S T,Corbet R H D,et a l.A p JS,2013,209:14

[21]Scarg le J D.A p J,1982,263:835

[22]F land rin P.T im e-frequency/T im e Scale A nalysis.San D iego:A cadem ic P ress,1998

[23]Lom b N R.A p&SS,1976,39:447

[24]Hasselm ann K.Theory.Tellus,1976,28:473

[25]Rob inson P M.Stochastic P rocesses and their A pp lications,1977,6:9

[26]M udelsee M.CG,2002,28:69

[27]P ress W H,Teuko lsky S A,Vetterling W T.Num erical Receipes in C.Cam b ridge:Cam b ridge Un iversity P ress,1996:702

[28]Foster G.A J,1996,111:541

[29]Foster G.A J,1996,112:1709

[30]Thom son D J.JM PS,1990,330:601

[31]Cherepashchuk A M,Sunyaev R A,M olkov S V,et a l.M NRAS,2013,436:2004

[32]Trushkin S A,Bu rsov N N,Sm irnova Y V.A st.Rep.,2001,45:804

[33]Corbet R H D,K rimm H A.A J,2013,778:45

[34]K atz J I,Anderson S F,G rand i S A,et a l.A p J,1982,260:780

[35]K atz J I.A p J,1997,478:527

[36]Begelm an M C,Hatchett S P,M cK ee C F,et a l.A p J,1980,238:722

Period icity A nalysis of X-ray Light Cu rves of SS 433

WANG Jun-yi1,2LU Xiang-long1,2,3ZHAO Qiu-wen3DONG Dian-qiao1,2,3LAO Bao-qiang3LU Yang3WEIYan-heng3WU Xiao-cong3AN Tao3

(1 G uangxi Experim en t Cen ter of In form a tion Scien ce,G u ilin U n iversity of E lec tron ic Techno logy, G uilin 541004) (2 G uangxi K ey Labo ra to ry of C ryp tography an d In fo rm a tion Secu rity,G u ilin Un iversity of E lec tron ic Techno logy,G u ilin 541004) (3 Shanghai A stronom ica l O bserva tory,Chinese A cadem y of Scien ces,Shanghai 200030)

SS 433 is the only X-ray binary to date that was detected to have a pair ofwell-collimated jets,and its orbital period,super orbital period,and nutation period were all detected at the same time.The study on the periodic X-ray variabilities is help ful for understanding its dynam ic process of the central engine and the correlation with other bands.In the present paper,two time series analysis techniques,Lomb-Scargle periodogram and weighted wavelet Z-transform,are em p loyed to search for the periodicities from the Swift/BAT(Burst A lert Telescope)(15–50 keV)and RXTE/ASM (Rossi X-Ray Tim ing Explorer/All-Sky Monitor)(1.5–3,3–5 and 5–12 keV)light curves of SS 433,and the M onte Carlo simulation is performed.For the 15–50 keV energy band,five significant periodic signals are detected,which are P1(～6.29 d),P2(～6.54d),P3(～13.08 d),P4(～81.50 d),and P5(～162.30 d).For the 3–5 and 5–12 keV energy bands,periodic signals P3(～13 d)and P5(～162 d)are detected in both energy bands. However,for the 1.5–3 keV energy band,no significant periodic signal is detected.P5has the strongest periodic signal in the power spectrum for all the energy bands of 3–5,5–12,and 15–50 keV,and it is consistent with that obtained by previous study in optical band.Further,due to the existence of relativistic radio jets,the X-ray and optical band variability of P5(～162 d)is probably related to the precession of the relativistic jets.High coherence between X-ray and optical light curvesmay also imply that the X-ray and optical em issions are of the same physical origin.P3shows a good agreement with the orbital period(～13.07 d)first obtained by previous study,and P2and P4are the high frequency harmonic components of P3and P5,respectively.P1is detected from the power spectrum of 15–50 keV energy band on ly,and it is consistent with the systematic nutation period.As the power ofenergy band decreases(from hard X-ray to soft X-ray),less periodicities are detected,which provides an evidence that the em ission from high energy band(hard X-ray)comes primarily from jets,and the em ission from low energy band(soft X-ray)m ay originate from the m edium around binary systems.Themultiple X-ray periods obtained from the present studies provide the necessary basis for the analysis ofmu lti-wavelength data and the dynam ics of the central engine system of SS 433.

star:binary,period,methods:wavelet transform,Lomb-Scargle periodogram,autoregressive process

P144;

A

10.15940/j.cnki.0001-5245.2016.02.002

2015-08-03收到原稿,2015-11-08收到修改稿

∗国家自然科学基金项目(61261017)、广西省自然科学基金项目(2013GXNSFAA 019334)、广西信息科学实验中心项目、广西无线宽带通信与信号处理重点实验室项目(GXKL0614202、GXKL0614101)、“认知无线电与信息处理”教育部重点实验室基金项目(CRKL150112)、北京邮电大学泛网无线通信教育部重点实验室项目(KFKT-2014102)和移动云动态应用卸载决策和传输调度优化研究项目(YJCXS201523)资助

†wangjy@guet.edu.cn