一种实时GNSS时间传递算法∗

于合理郝金明谢建涛田英国陈逸伦

(1信息工程大学导航与空天目标工程学院 郑州 450052)

(2北斗导航应用技术河南省协同创新中心 郑州 450052)

一种实时GNSS时间传递算法∗

于合理1,2†郝金明1,2谢建涛1,2田英国1,2陈逸伦1

(1信息工程大学导航与空天目标工程学院 郑州 450052)

(2北斗导航应用技术河南省协同创新中心 郑州 450052)

针对载波相位时间传递算法的局限性,提出了一种实时GNSS(Global Navigation Satellite System)时间传递算法,通过共视(Common View,CV)卫星建立站间非差观测方程的联系,联合解算卫星钟差和站间时间传递结果.该算法不需要卫星精密钟差产品,仅用卫星精密轨道信息直接计算得到站间时间传递结果,不受卫星钟差内插精度、采样率的限制.该算法与通过站间单差将卫星钟差参数进行消除的传统共视算法不同,是将卫星钟差参数进行实时解算得到的.实验结果表明:该算法时间传递精度与传统的GNSS载波相位(Carrier Phase,CP)算法相当,比较适用于实时时间传递.

天体测量学,时间,技术:其他诸多方面,方法:数据分析

1 引言

自1980年Allan和Weiss首次提出了利用GPS(Global Positioning System)共视技术进行时间传递的方法以来,GNSS技术迅速成为时间传递的主要手段之一.利用GNSS进行时间传递主要有GNSS共视、GNSS全视(All in View,AV)和GNSS载波相位法.GNSS CV法和AV法均采用伪距码观测值作为观测量,授时精度仅为纳秒量级.GNSS CP技术是在AV技术的基础上,增加载波相位观测量,使用载波相位和伪距码的组合观测量,授时精度为亚纳秒量级,是精度最高的GNSS时间传递技术之一[1–5].CP法是单站作业,无法有效消除中短距离内站间时间传递的相关误差,且CP法需要使用国际GNSS服务组织(International GNSS Services,IGS)提供的事后精密轨道和钟差产品,其应用主要停留在事后处理模式上,实时应用未能得到广泛开展.卫星轨道由于变化平缓可以预报,目前IGS提供的超快速预报轨道精度为5 cm,可以满足实时需要.然而,由于卫星钟差变化复杂而难以准确预报,使超快速钟差产品精度较低,仅为3 ns左右,远低于事后精密钟差产品,对时间传递结果的影响可达数纳秒,且误差会随时间的延长呈线性增长,不能满足实时时间传递的需要[6–8].为此,本文提出了一种实时GNSS时间传递算法,该算法与传统CP算法相比,通过共视卫星建立两测站观测方程间的联系,不需要卫星精密钟差产品,不受钟差内插和采样率限制;与传统的CV算法相比,虽然都不需要精密钟差产品,但处理方法略有不同.传统的CV算法是通过测站间作差消除卫星钟差,而本文算法是将卫星钟差作为参数在线解算,通过共视卫星联合建立两测站观测方程之间的联系,同时解算卫星钟差参数和站间时间传递结果.

2GNSS CP算法

GNSS CP算法一般采用PPP(Precise Point Positioning)算法[1–6],其误差方程如下:

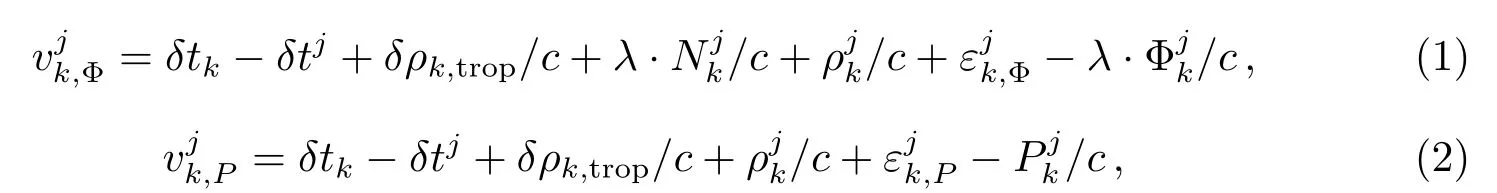
其中,k为测站号,j为卫星号,δtk、δtj分别为接收机和卫星钟差,δρk,trop为对流层延迟, c为光速,λ为波长,为接收机到卫星的几何距离,为消电离层组合的模糊度,、分别表示相位和伪距消电离层组合观测值;为观测误差;表示未模型化的误差影响.

PPP解算得到的实际上是观测站接收机钟相对于GNSS系统时间的偏差,即δtk是测站k接收机钟相对于GNSS系统时间的相对钟差,采取同样的方法可以得到测站l接收机钟相对于GNSS系统时间的相对钟差δtl.两站钟差值相减即可消去GNSS系统时间的影响,得到两站站间时间传递结果δtlk:

3 实时GNSS时间传递算法

为克服PPP算法对外部精密卫星钟差产品的依赖性,提出了一种实时时间传递算法.该算法基于IGS卫星精密轨道信息,通过构建不同测站观测方程之间的联系,联合解算测站接收机钟差和卫星钟差实现测站间时间传递.该算法将卫星钟差当作未知参数,不需要使用卫星精密钟差产品,仅利用卫星精密轨道信息和两个测站观测数据,通过联合解算方式直接获得两测站间的时间传递结果.目前IGS提供的超快速预报轨道精度可以满足实时需要,在实时时间传递中可以利用超快速预报轨道产品进行解算[8−9].

该方法需要首先选定一个测站k,将测站k的接收机钟定为基准钟来同时解算测站l接收机钟和卫星钟相对于基准钟的相对钟差,则有:

选定基准钟后即可给出各测站的误差观测方程,此时,基准钟测站k观测方程不再包含接收机钟差参数,只含有卫星钟差、模糊度和对流层参数.(1)–(2)式相应的观测方程变为:

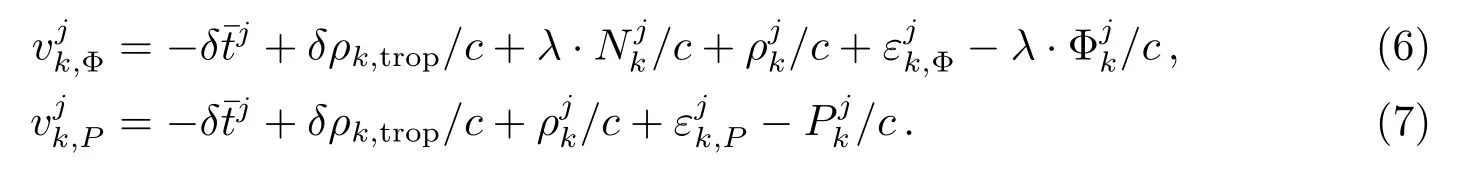
选定测站k为基准钟后,测站l有类似形式的观测方程,但是增加了接收机钟差参数作为未知参数.此时,接收机钟差和卫星钟差参数均是相对于测站k基准钟的相对钟差,误差方程变为:

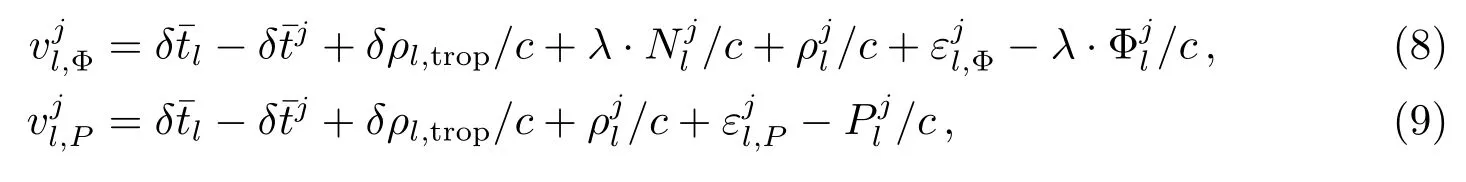
联立(6)–(9)式即可直接解算得到站间时间传递结果.由(6)–(9)式明显可以看出,只要测站l和测站k之间有足够的共视卫星,两测站非差观测方程就可以通过同时估计的卫星钟差联系在一起,联立两测站的误差方程同时解算卫星钟差和站间时差即可直接得到站间时间传递结果.这种站间实时GNSS时间传递算法不需要精密钟差产品,不受钟差内插精度、采样率的限制,只受各测站观测数据采样率限制,只要两测站间有足够的公共卫星就能实现时间传递.在实时时间传递中,可以采用超快速预报轨道进行解算.

4 实验分析

为了验证文中所给方法的有效性,采用2015年6月10日的图卢兹(TLSE)和圣费尔南多(SFER)两IGS观测站的数据进行实验分析,两站相距1 067 km,数据采样间隔为30 s.目前,IGS提供的事后精密钟差产品精度为75 ps,本文将其作为“真值”进行比对[10–16],设计了两种方案进行实验分析.

方案1:两测站采用GNSS CP算法进行时间传递,两站分别利用IGS事后精密轨道和精密钟差产品进行PPP解算,对获得的两测站授时结果作差,获得站间时间同步结果.

方案2:采用本文提出的站间时间传递算法,直接获得两站的时间传递结果.选择TLSE站作为基准站,TLSE站的接收机钟作为基准钟,卫星轨道采用超快速轨道,卫星钟差不是由精密钟差产品内插得到的,而是作为未知参数和测站钟差一起估计.

将两种方案计算得到的SFER站和TLSE站的站间时间同步结果和IGS“真值”进行比较,其时间序列如图1(a)所示.为了便于区分3种时间同步结果,更好地分析两种方案计算的时间同步结果,图1(b)给出了方案1站间同步结果统一加上8 ns,方案2站间时间同步结果统一减去8 ns后与IGS时间序列对比图.

由图1可知方案1、方案2站间时间同步结果与IGS结果变化趋势十分一致,且时间同步结果与IGS结果符合较好.为进一步分析两种时间传递方案结果的精度,将两种方案得到的时间同步结果与IGS“真值”作差,得到两种方案时间同步结果残差序列,如图2所示,图中纵坐标V表示两种方案得到的时间同步结果减去IGS真值得到的残差.表1为两种方案得到的时间同步结果的统计情况.

根据图1、图2和表1可知,两种方案时间同步结果变化趋势均与IGS事后“真值”变化趋势一致,且两者时间同步结果残差变化趋势也基本一致.两种方案得到的结果无论是均方根误差RMS还是标准差SD都相差很小,均在0.03 ns左右,精度基本相当,方案2得到钟差序列的离散程度(标准差SD)略优于方案1,相对较为稳定.但方案1由于需要事后精密卫星钟差产品,只适用于事后处理,而方案2不仅能应用于事后时间传递,还比较适用于实时时间传递.综上可知本文提出的实时GNSS时间传递算法可以用于站间实时时间传递,精度与GNSS CP算法相当.

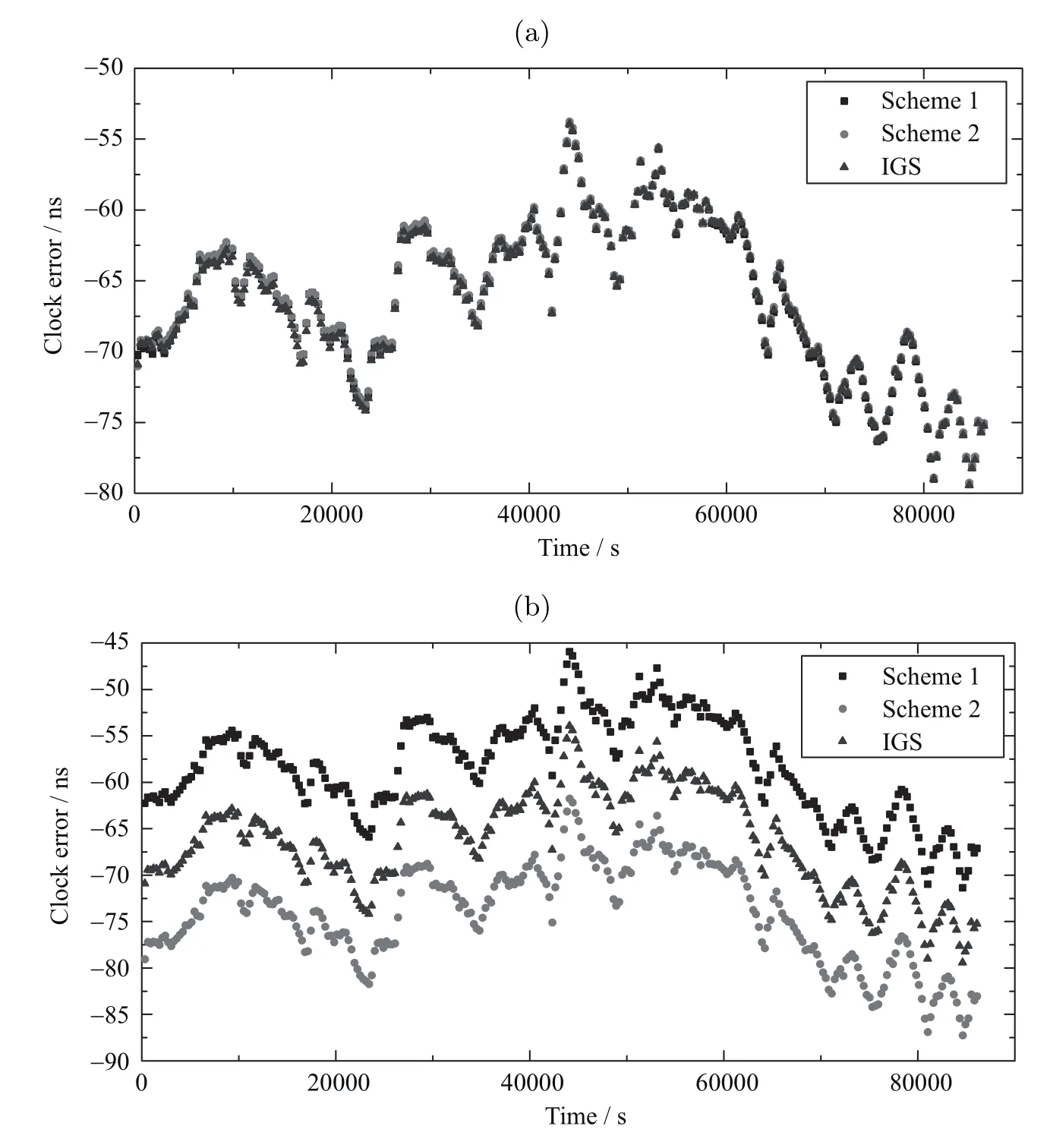
图1 两种方案结果与IGS时间序列对比.(a)为原始序列与IGS时间序列对比图,(b)为方案1和方案2分别加上8 ns和−8 ns后与IGS时间序列对比图.Fig.1Comparison of the results based on two schemes and the IGS real values.(a)comparison of the original sequence and IGS time series,(b)the constants of 8 ns and−8 ns are added to the results of schemes 1 and 2 in comparison with the IGS time series,respectively.

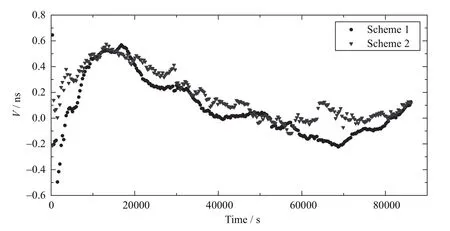
图2 两种方案时间同步结果残差图Fig.2 Residuals of the time transferring results with two schemes

表1 两种方案时间同步结果精度(单位:ns)Table 1 Accuracies of the time transferring results with two schemes(unit:ns)

5 结论

GNSS CP技术受事后精密卫星钟差产品实时性和精度影响,其实时应用受到很大限制.本文提出的基于卫星精密轨道的站间GNSS时间传递算法,与GNSS CP(PPP)算法相比,不需要卫星精密钟差产品,不受钟差内插和采样率限制;与传统的共视算法通过站间作差方式消除卫星钟差不同,该算法是将卫星钟差作为未知参数进行在线解算,通过共视卫星构建两测站观测方程之间的联系,利用精密卫星轨道和测站伪距及载波相位观测数据,联合解算卫星钟差和站间时差,直接计算得到站间时间传递结果.在实时应用中,利用超快速预报轨道,能够得到较为稳健的时间传递结果,其精度主要取决于两测站间是否有足够多的共视卫星.实验表明:本文算法的时间传递精度与PPP算法基本相当,可以达到0.3 ns以内,能够应用于实时高精度时间传递.

[1]许龙霞.基于共视原理的卫星授时方法.北京:中国科学院国家授时中心,2012:5-13

[2]Levine J.Metro,2008,45:162

[3]Dach R,Hugentobler U,Schildknecht T,et al.Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition,2005:329

[4]张小红,程世来,李星星,等.武汉大学学报:信息科学版,2009,34:463

[5]Khoshmanesh M,Hossainali M M.Arabian Journal of Geosciences,2014,7:4819

[6]陈宪冬.武汉大学学报:信息科学版,2008,33:245

[7]于合理,郝金明,刘伟平,等.大地测量与地球动力学,2014,34:161

[8]黄观文.GNSS星载原子钟质量评价及精密钟差算法研究.西安:长安大学,2012:81-113

[9]Salazar D J,Advisor H,Jaume S,et al.Precise GPS-based Position,Velocity and Acceleration Determination:Algorithms and Tools.Barcelona:Universitat Politecnica de Catalunya,2010:74-80

[10]Cerretto G,Perucca A,Tavella P,et al.Time and Frequency Transfer through a Network of GNSS Receivers Located in Timing Laboratories.Frequency Control Symposium,2009 Joint with the 22nd European Frequency and Time Forum,2009:1097

[11]闫伟.武汉大学学报:信息科学版,2011,36:648

[12]雷雨,赵丹宁.天文学报,2014,55:216

[13]梁月吉,任超,杨秀发,等.天文学报,2015,56:264

[14]Liang Y J,Ren C,Yang X F,et al.ChA&A,2016,40:79

[15]高玉平.天文学报,2004,45:428

[16]Gao Y P.ChA&A,2005,29:213

A Real-time Algorithm of GNSS Time Transfer

YU He-li1,2HAO Jin-ming1,2XIE Jian-tao1,2TIAN Ying-guo1,2CHEN Yi-lun1
(1 School of Navigation and Aerospace Engineering,Information Engineering University,Zhengzhou 450052)
(2 Beidou Navigation Technology Collaborative Innovation Center of Henan,Zhengzhou 450052)

For the limitations of current algorithms of carrier-phase time transfer, a real-time algorithm of GNSS(Global Navigation Satellite System)time transfer is proposed.Using the relations between un-di ff erenced observation equations which are established through the common view satellite,the results of the satellite clock o ff set and inter-station time transfer can be calculated at the same time.This method obtains the result of inter-station time transfer only by the satellite ephemeris without using the satellite precise clock products,and it is not limited by the satellite clock error and sampling rate.Di ff erent from the traditional common view method in which the parameters of satellite clock o ff set are eliminated by the single di ff erence,the real-time satellite clock o ff sets are estimated in this algorithm.Experiment results show that the accuracy of time transfer of the proposed algorithm is the same as that of the GNSS carrier phase algorithm,and this algorithm is more suitable for the real-time time transfer.

astrometry,time,techniques:miscellaneous,methods:data analysis

P128;

:A

10.15940/j.cnki.0001-5245.2016.03.007

2015-10-15收到原稿,2015-11-18收到修改稿

∗中国第二代卫星导航系统重大专项课题(GFZX0301040308-03、GFZX0301040101ZX04、GFZX0301040107)、地理信息工程国家重点实验室开放研究基金项目(SKLGIE2015-M-1-6)资助

†yuhl1989@163.com