固定翼无人机定点飞行最优路径选择
梁 爽
(大连大学电子信息工程学院,辽宁 大连 116622)
固定翼无人机定点飞行最优路径选择
梁爽
(大连大学电子信息工程学院,辽宁 大连116622)
摘要:针对固定翼无人机路径规划复杂、航迹冗余、偏离度高等特点,通过建立三维空间空气动力学模型,标定预置坐标,根据常规气动布局下的空气动力学原理、PID算法、环境等因素对航迹网格点进行管理。采用改进的动态规划算法,对如何准确、快速地计算出连贯预定坐标的最佳路径进行了研究。飞控计算机通过动态对比、状态预测算法,对路径进行实时对比、矫正、重新规划,使无人机能沿着贯穿预定坐标的最佳路径完成既定飞行任务。
关键词:无人机固定翼航迹优化最优路径预定坐标空气动力学模型PID状态预测动态对比
0引言
无人机执行任务时,通常伴随着复杂的航迹变化。能源限制使得滞空时间变得相对固定,最大限度地优化航迹可以大幅度延长执行任务时间,所以无人机,尤其是小型无人机对于航迹的优化有着迫切的需求。随着传感器工艺的发展,传感器愈发趋于多元化、小型化、高精化,使得对无人机飞行时的位置、姿态信息能够精确掌握。同时中央处理器处理能力的提升,也为无人机最优航迹的即时计算提供可能。飞行前,地面控制站给出空中预定坐标,并结合飞机的机动能力、空气动力学模型计算最佳航迹[1]。在飞行过程中,随着环境因素的改变,实际飞行路径或存在误差。通过动态对比算法[2]、状态预测算法对无人机航迹进行实时调整,可大幅度精简无人机飞行路径,延长执行任务时间。
1最佳路径选定
1.1无人机模型
无人机的空气动力学和运动学模型[3]如图1所示。

图1 无人机模型

(1)
式中:(x,y,z)为惯性坐标系下飞机的位置;θ为航向角;φ为俯仰角;v为速度;ω为角速度;m为质量;J为转动惯量;F为控制力;M为控制力矩[4]。
1.2路径描述
飞机与下一个参考点保持一个相对距离,飞机运动过程保持期望的路径运动[5]。该路径由参数ψ表示:Pd(ψ)=[ xd(ψ),yd(ψ),zd(ψ)]。路径上每一点都有一个给定的速度vs(ψ),如图2所示。

图2 飞行路径示意图
无人机的期望路径为:
Pd= Pd(ψ)+R[θd(ψ),φd(ψ)]l
(2)
式中:Pd(ψ)为飞机对ψ的信息;R[θd(ψ)φd(ψ)]为由无人机的体坐标系到惯性坐标系的转换矩阵。
(3)

为了检验期望路径的准确性,通过给定若干个坐标点,根据上述公式计算出期望路径,并与软件仿真路径作对比,如图3所示。

图3 实验仿真图
由图3可以看出,通过计算得到的期望路径,基本与软件仿真路径相重合,表明了本文建立的模型以及路径跟踪算法的有效性。
2硬件结构
硬件系统主要包括无人机地面控制站、无人机平台、飞控系统、传感器、动力系统、伺服系统、任务载荷[7],硬件结构如图4所示。

图4 硬件结构图
无人机平台起飞前,由地面控制站根据预置坐标计算初始最优路径,并将预置坐标、初始最佳路径、任务数据发送至位于无人机平台上的飞控系统。无人机升空后,飞控系统读取传感器数据,确定无人机位置、姿态,并通过控制动力系统、伺服系统,实现对最佳路径的跟踪。当飞机大幅度偏离最佳路径时,飞控计算机对已通过的预置坐标比对,并基于当前位置计算出贯穿剩余预置坐标的最优路径[8]。
3软件结构
通过软件控制,实现对无人机空中最优路径的跟踪与重新计算。软件系统包括地面控制站软件与无人机平台软件。地面控制站软件流程如图5所示。

图5 地面控制站软件流程图
启动地面控制站后,操控员输入任务指令和预置坐标,地面控制站自动计算出初始最优路径;控制站向无人机发送自检命令,如果无人机自检未通过,则地面控制站显示故障位置后结束任务规划操作;自检通过后,控制站向无人机发送任务指令、预置坐标、初始最优路径。若未发送成功,将再次发送自检指令;发送成功后,控制站发送起飞指令,无人机升空,任务规划完成。无人机平台软件流程如图6所示。
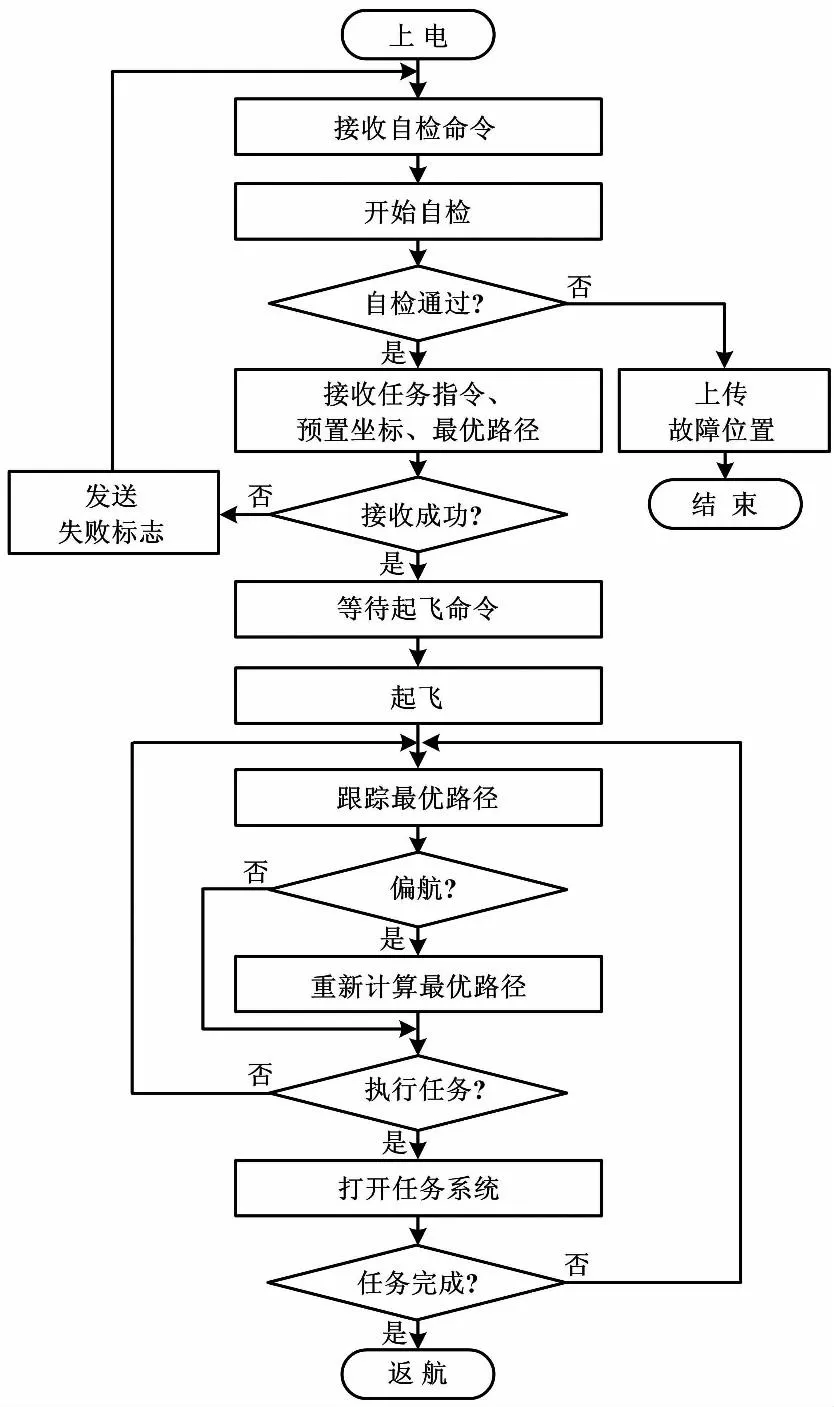
图6 无人机平台软件流程图
无人机系统上电,收到地面控制站的自检指令后开始自检;若未通过,则上传故障位置。通过自检后,无人机接收任务指令、预置坐标、最优路径。若接收失败,则上传失败标志;若接收成功,无人机平台在接收到地面控制站的起飞命令后升空执行任务。起飞后,无人机通过姿态控制跟踪最优路径。若偏离最优路径,则基于当前位置计算出贯穿剩余预置坐标的最优路径。到达任务区域后,无人机平台打开任务系统,在任务执行完毕后,无人机返航。
4结束语
本文提出的无人机固定翼无人机空中定点飞行最优路径选择方法,通过快速建立三维空间中空气动力学模型、标定预置坐标,并根据费马原理和改进的动态规划方法,计算出执行任务的最优路径,能够有效延长执行任务时间。同时,本文还论证了无人机对最优路径的跟踪问题,最大程度地降低飞行过程中由于突发情况产生的对于最优路径的重新计算,降低飞控计算机的计算量,提高实际飞行路径与最优路径的契合度。文中没有考虑到由于不可抗力导致无人机偏离最优路径时,飞控对路径进行重新绘制的问题,这也是下一步需要研究的方向。
参考文献
[1] 张建中,陈世军,余大祥.最短路径射线追踪方法及其改进[J].地球物理学进展,2003(18):146-150.
[2] 廖慧芬,邵小兵.动态规划算法的原理及应用[J].中国科技信息,2005(21):42-42.
[3] 荣辉,李冬,殷堂春.基于Matlab无人机数学模型仿真分析与研究[J].科学技术与工程,2008(8):1510-1512.
[4] Martins W S,Del Cuvillo J B,Useche F J,et al.A Multithreaded Parallel Implementation Of A Dynamic Programming Algorithm For Sequence Comparison[C]// In Pacific Symposium on Biocomputing,2001:311-322.
[5] Nordbruch S,Galbas R,Ruehle A.Method and control device for highlighting an expected movement path of a vehicle: US,US20130054089 A1[P].2013.
[6] 张燕,徐德民.移动机器人路径跟踪控制方法研究[J].机电一体化,2008(6):48-51.
[7] 谭和林,夏道军,赵婉.小无人机系统总体技术探析[J].科技风,2013(16):12-12.
[8] Wang Sheng,Li Lemin.An enhanced algorithm for multiple constraints optimal path calculation[C]// Communications,Circuits and Systems,2004.
Selection of the Optimal Path for Established Flight Mission of Fixed-wing UAV
Abstract:For the features of fixed-wing UAV,e.g.,complex path planning,redundant flight track,and high degree of deviation,through setting up the aerodynamics model of three-dimensional space,calibrating the preset coordinates,and according to the factors of aerodynamic principle,PID algorithm,and environment under conventional aerodynamic layout,the flight track grid points are managed.With the improved dynamic planning algorithm,the method for accurately and quickly calculating the optimal path of coherence predetermined coordinates is researched.The paths are compared,corrected and re-planned in real time by flight control computer through dynamic contrast and state prediction algorithms,thus the UAV can accomplish the established flight mission along the optimal path with predetermined coordinates.
Keywords:Unmanned-aerial-vehicle(UAV)Fixed-wingFlight track optimizationOptimal pathPredetermined coordinateAerodynamic modelsPIDState predictionDynamic contrast
中图分类号:TH86;TP27
文献标志码:A
DOI:10.16086/j.cnki.issn1000-0380.201605004
修改稿收到日期:2016-02-18。
作者梁爽(1992-),女,现为大连大学电子信息工程专业在读本科生;主要从事自动控制、通信技术方向的研究。

