扬起“想象”之帆
信红艳


想象是思维探索的翅膀。爱因斯坦说:“想象比知识更重要,因为知识是有限的,而想象可以包罗整个宇宙。”我在教学平面图形面积计算综合复习一课时,在夯实认知基础的前提下,将学过的长方形、平行四边形、三角形、梯形面积计算公式进行融会贯通,引导学生进行数学想象,缩短了解决问题的时间,使学生获得数学发现的机会,锻炼了他们的数学思维。
一、形成完整的知识体系,沟通面积计算公式之间的内在联系
我在教学长方形、平行四边形、三角形、梯形面积计算公式之后,提出这样的问题:请同学们回忆一下,我们刚刚学过的平行四边形、三角形、梯形的面积公式是怎样推导出来的?
生1:平面图形的面积计算公式都是以长方形的面积计算方法为基础推导出来的,正方形是长方形的特例。
生2:平行四边形的面积公式是用割补法转化成长方形而推导出来的。
生3:三角形、梯形的面积计算公式是通过两个完全一样的三角形、两个完全一样的梯形拼合成平行四边形而推导出来的。
这时,我引导学生进行思考,把面积计算知识系统化,沟通这几种图形面积公式之间的内在联系。我又提出了这样的问题,就梯形面积公式而言,请同学们想象一下:
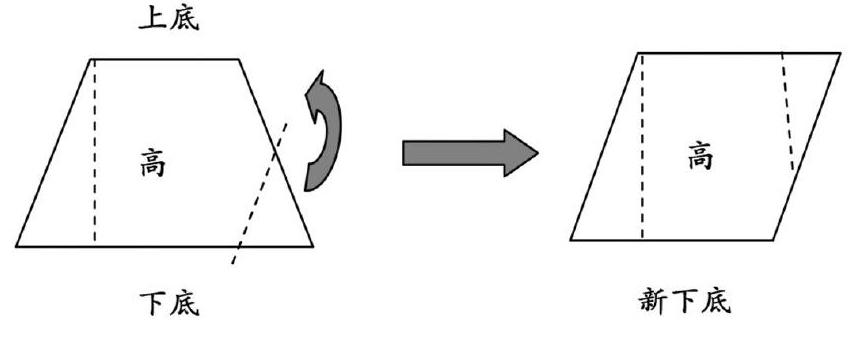
1.如果把梯形的上底变得与下底同样长,这时变成什么图形?与梯形面积有什么关系?
2.如果把梯形上底缩短为0,这时又变成了什么图形?与梯形面积有什么关系?
问题的提出使学生想象的闸门打开了,为学生创造了自主学习的空间。
学生以小组为单位,立刻动起手来,每小组的6名成员分好工,拿出提前准备好的图形卡片剪的剪、拼的拼,并热烈地讨论起来。10分钟后,各小组操作讨论基本完成,开始汇报。
生1:将梯形的上底变得与下底一样长,可以剪掉一个以“上底-下底”为底,与原梯形等高的三角形,此时剩余部分可以看作上底与下底同样长的梯形,已经变成了平行四边形;由于被剪掉一部分,所以面积变小了。面积计算按梯形面积公式计算应该是:面积=(上底+下底)×高÷2=2×上底×高÷2=底×高,这不就是平行四边形的面积公式吗?
生2:我们小组是这样讨论的,沿着梯形一个腰的中点平行于另一个腰剪下一个小三角形,以这一个腰的中点为中心,将小三角形逆时针旋转180ο,就转化成一个与原来梯形面积相等的平行四边形。这个新平行四边形的底等于原梯形的上底与下底之和的一半,面积计算按梯形面积公式计算应该是:面积=(新上底+新下底)×高÷2=2×新下底×高÷2=底×高,这不也是平行四边形的面积公式吗?
生3:将梯形的上底缩短为0,须要剪掉一个以上底为底,与原梯形等高的平行四边形,此时剩余部分可以看作上底为0的梯形,已经变成了三角形;由于剪掉了一部分,所以面积变小了。面积计算按梯形面积公式计算应该是:面积=(0+下底)×高÷2=下底×高÷2,这不就是三角形的面积公式吗?
生4:我们小组是这样讨论的:沿着梯形上底的一个顶点与对腰中点连线剪下一个小三角形,以这一腰的中点为中心,将小三角形顺时针旋转180ο,就转化成一个与原来梯形面积相等的三角形。面积计算按梯形面积公式计算应该是:面积=(0+上底+下底)×高÷2=新下底×高÷2,这不也是三角形的面积公式吗?
生5:原来我们学过的这些平面图形的面积计算公式有这样内在的联系。
生6:这样我们就不用死记硬背这些公式了。
生7:我明白了为什么三角形和梯形的面积公式有除以2,而平行四边形的面积公式没有除以2。
二、数学想象的几个基本要素
以上教学过程,培养了学生想象思维的能力,理清了思路,又渗透平移、转化等数学思想,发展了学生的思维,提高了学生的自学能力,拓宽了学生的思维空间。在教学中,引导学生进行数学想象,往往能缩短解决问题的时间,获得数学发现的机会,锻炼数学思维。本节课体现了数学想象的几个基本要素。
1.因为想象往往是一种知识飞跃性的联结,因此要有扎实的基础知识和丰富的经验的支持。
2.要有能迅速摆脱表象干扰的敏锐的洞察力和丰富的想象力。
3.要有执着追求的情感。
陶行知先生的“创造的儿童教育”提出了6大解放:
1.解放儿童的头脑,使他能想。
2.解放儿童的双手,使他能干。
3.解放儿童的眼睛,使他能看。
4.解放儿童的嘴,使他能谈。
5.解放儿童的空间,使他能到大自然大社会里取得更丰富的学问。
6.解放儿童的时间,使他们有自己的时间去做自己喜欢做的事情。
以上6个解放是陶行知先生留给我们广大教师宝贵的教学经验。因此,我在以上教学环节中,充分融入了这一教学理念,培养学生的想象力。首先通过回忆旧知唤醒并夯实了学生的有关认知基础;其次,新知识的产生除去推理外,常常包含前人的想象因素,因此在教学中根据教材潜在的因素,创设想象情境,提供想象材料,诱发学生创造性想象。
(作者单位:大庆一中实验一小)

