由一道概率考研题引发的思考和探究

孔令仪

摘 要： 由2015全国硕士研究生入学统一考试数学（一）中的第22题，引发了关于求解一类概率题的思考和探究.本文通过举例说明在求解此类问题时，要在准确理解题意的基础上，紧扣相关的基本概念及性质将问题化繁为简，才是解决此类复杂概率问题的捷径，也是切实灵活掌握相关知识的行之有效的方法.

关键词： 概率密度函数 独立同分布 数学期望 几何分布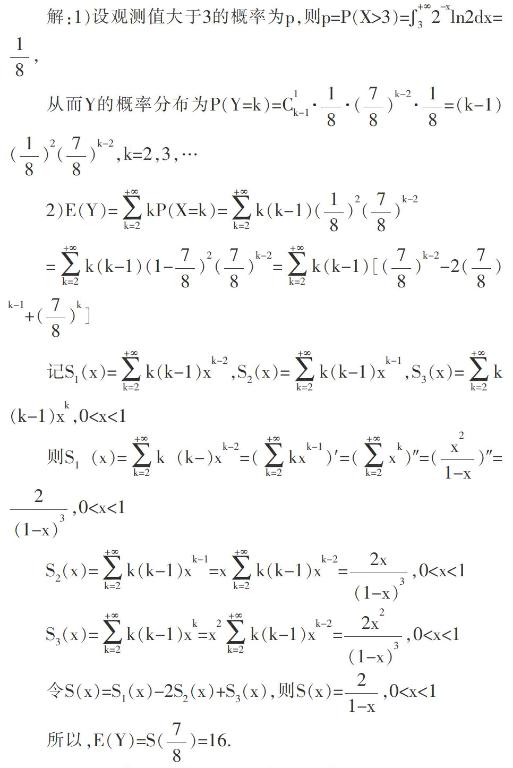

1.一道概率考研题及其常规解法

为了便于说清问题，先给出这道概率考研题及其常规（常见）解法.

本题的问题1）是概率论的常见题型，方法也是基本固定的，不是本文讨论的重点.问题2）是概率论中一种重要的题型，但对不同的问题，方法多种多样，难易、繁简程度相差很大.就问题2）来说，经查阅相关资料[1]，[2]，发现与上面的解法大同小异，基本相同.此种解法，虽然用到的概率知识仅是数学期望的定义，但求解的过程比较繁琐，用到的解题技巧较多，还要用到求函数项级数的和函数等高等数学知识.如果说再用这种方法求解方差D（Y）的话，计算就会变得更复杂、更繁琐.

2.常规解法的不易引发的时刻和探究

从以上常规的求解方法可看出，此种解法计算量大且较复杂.现在将问题再推广，将“直到第2个大于3的观测值出现时停止”改为“直到第n个大于3的观测值出现时停止”，如果还是用以上的常规解法，计算的复杂性和计算量就会急剧增加，变得非常复杂且困难.这显然不是一种好方法.

经过思考，我们发现如果结合概率论中已有的相关结果，紧扣题意并恰当利用随机变量数字特征（如数学期望、方差等）的性质，此类题型的求解就是有章可循的，且求解过程简单明了、计算量小，也便于推广.下面将例题1的问题2）进行适当推广并求解，具体见以下例题2.

参考文献：

[1]新东方在线.2015年考研数学一真题及答案[EB/OL].[2016-04-03].http：//kaoyan.eol.cn/shuxue_3976/20141229/t2014 1229_121944012.shtml.

[2]中公教育.2015考研数学（一）真题答案及解析[EB/OL].[2016-04-03].http：//learning.sohu.com/20141228/n407347641. shtml.

[3]孔告化，何铭，胡国雷.概率统计与随机过程（修订版）[M].北京：人民邮电出版社，2012.9.