多孔介质毛细升高特性的研究

陈 威 凌娟娟 赵群力 上海海事大学 商船学院



多孔介质毛细升高特性的研究

陈 威 凌娟娟 赵群力 上海海事大学 商船学院

摘要：在考虑重力的基础上，为研究多孔介质内部液相为非饱和状态下的毛细升高特性，建立数学模型，得出毛细升高高度与时间的函数关系。以多孔陶瓷管为实验对象，验证模型正确性并分析毛细升高高度变化的影响因素。结果表明颗粒直径越小，最终毛细升高的高度越大；在液体可流动的范围内，饱和度越低，其毛细升高高度越高；多孔介质倾斜角的大小影响毛细升高的长度，但初期的长度相同。

关键词：多孔介质；毛细升高；颗粒直径；饱和度

Fund Item：National Nature Science Foundation in China （51276107），Shanghai Municipal Education Commission Scientific Research Topic（14ZZ142），Transportation Minister Application Fundamental Project （2013319810150）

陈威：（1986-），男，博士，教授。

近年来多孔介质中的传热传质问题广泛应用于工农生产中的各个领域，如：食品和药品的干燥、土壤学、热管技术、多孔介质被动蒸发冷却技术等。但多孔介质内部孔隙结构比较复杂，对流传质规律具有很大的随机性。且热传递过程也较复杂，热传导发生在多孔介质骨架连接处或骨架与孔隙中的流体处；对流换热是由于多孔介质孔隙内水分的宏观运动。而多孔介质的毛细升高特性直接影响着其传热传质过程。因此，学者在研究多孔介质传热传质的机理时，首先要对多孔介质毛细升高特性进行研究，并与实验结果进行对照，从而用于实践。同时，多孔介质毛细升高的研究还可以为电子器件冷却、石油的开采等提供指导，具有很强的研究意义。

1　数学模型

多孔介质体系由固体骨架、水蒸气、空气、液态水等构成，多孔介质内部结构非常复杂，不利于建立合适模型。为方便多孔介质圆管毛细升高数学模型的建立，现作如下假设：

（1）多孔介质视为均质、无变形、各项同性的材料［1］；

（2）多孔介质内液相和气相各自连续，且液相和固体骨架相连，空气和固体骨架不相连；

（3）多孔介质内液体饱和度为定值，不随高度的变化而变化；

（4）多孔介质圆管内孔隙为连通圆柱形，直径不随高度的变化而变化；

（5）多孔介质内部流动为一维流动，即认为沿管径方向没有流动；

（6）气液相交换时没有摩擦力和惯性力；

（7）毛细管压力可以通过静态接触角和孔径计算；

根据以上假设，多孔介质孔隙内，液体流动的动量方程为［2］：

式中σ为表面张力，R为孔径，ρ为液体密度，h为毛细升高高度，ψ为倾斜角，ε为孔隙率（有效孔隙率），为静态接触角。

由达西定律得，压力损失项为：

式中µ为动态粘度，vs为液体流动速度。哈根-泊肃叶定理数学表达式为：

式中L为管长，p∆为压力损失。

孔径与孔隙率及渗透率的关系为：

由于忽略惯性力，不再考虑式（1）中的惯性项。根据式（1）（2）解方程，为了简便计算，设中间项a、b。对于多孔介质有［1］：

式（5）中包含毛细压力项，表示为：

当多孔介质内为气液两相共存时，毛细压力可以表示为［3］：

式中 s为液相饱和度（多孔介质孔隙内液体所占体积与孔隙体积之比）。

用式（8）气液两相时的毛细压力替代式（7）中仅为液相时的毛细压力。则式（5）可表示为［3］：

当多孔介质孔隙内为单相流动时，渗透率可以由颗粒直径与孔隙率表达：

当多孔介质孔隙内为气液两相流动时，渗透率为：

为了简化计算过程这里引入朗伯W函数，其函数表达式为：

根据以上公式可求得液位随时间升高的函数（）h t为：

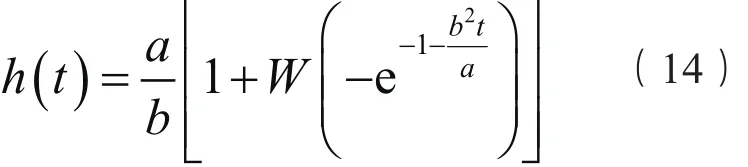
2　物理模型

如图1所示，取一多孔陶瓷管，将其完全干燥后竖直放入水槽中，向水槽中注入适量的水，使圆管底部刚好被水浸没。由于多孔材料管内部孔隙的毛细作用，水会向上运动。随着高度的上升，管内液体饱和度逐渐变小，当到达临界值时，液体便会停止上升，液位达到一个稳定的高度。由于多孔材料内部孔隙为开口式，对多孔介质内毛细升高高度的研究可以结合毛细管研究。

针对如图1所示的多孔介质圆管，本文使用MATLAB进行计算，根据以上数学模型编写程序求解式（14）。计算过程中采取控制变量法，即分别计算不同饱和度、倾斜角、颗粒直径下，多孔介质圆管毛细升高的高度。

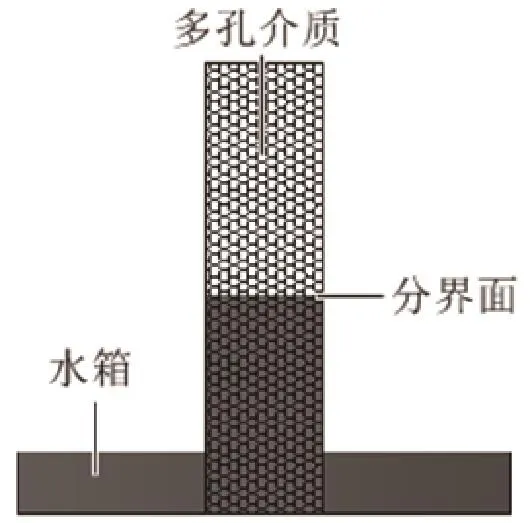
图1　多孔介质圆管吸水示意图

3　数值计算结果分析

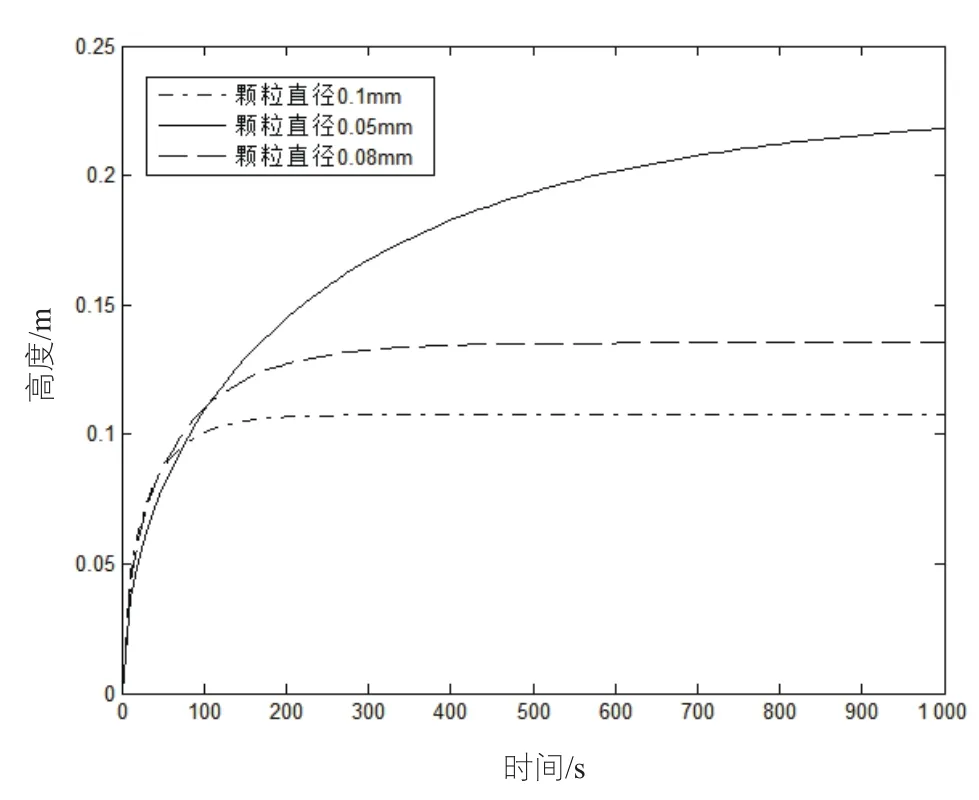
图2　不同颗粒直径时上升高度随时间变化

图3　不同饱和度时上升高度随时间变化

图2显示了饱和度为0.8，温度为317 K，竖直状态时不同颗粒直径对应的毛细升高情况。由图可知，不同颗粒直径时其最终稳定高度不同，颗粒直径为0.05 mm时上升高度最高为0.23 m；颗粒直径为0.08 mm次之，为0.13 m；颗粒直径为0.1 mm时最低，为0.11 m。当毛细升高开始阶段即100 s内时，不同颗粒直径毛细升高高度接近，100 s以后出现明显差异。其中颗粒直径为0.05 mm时，毛细升高速度前期比另外两种情况慢，100s以后上升速度超过另外两种情况。出现此现象的原因为：由式（12）可知，渗透率和颗粒直径成正比关系，颗粒直径的减小，导致渗透率减小，而渗透率即渗透速度。

图3显示当温度为317 K，颗粒直径为0.05mm，竖直放置时不同饱和度时毛细升高高度随时间变化的情况。从图中可知随着饱和度的降低，毛细升高速度依次增加，最后稳定的高度也依次增大。此处认为饱和度0.4在液相连续临界值以内。由于在毛细水上升的初始阶段，毛细水总量相对较少，黏性阻力及自身重力作用相对较小，毛细压力和毛细上升初期惯性力占主导作用，这种力能够平衡较多毛细水产生的重力，因此上升速度非常大。

图4　不同倾斜角时上升高度随时间变化

图4显示当饱和度为0.8，颗粒直径为0.05 mm，温度为317 K，不同倾斜角时毛细升高高度随时间变化的情况。从图中可以看出随着倾斜角的减小，多孔介质沿轴向上升的长度逐渐增加。并且毛细升高的速度随着倾斜角的减小而增加。这是由于动量方程中第二项与重力相关，当倾斜角减小时，粘性压力损失向增大，由于假设其它变量不变，故长度增大。

4　实验验证

为验证模拟分析的结果，需要实验测量微多孔陶瓷管的孔径和孔隙率。试验中使用电子天平、电热鼓风干燥箱、热成像仪和扫描电子显微镜等精密仪器，确保了实验数据的准确性和可靠性。同时，要测量多孔陶瓷管毛细升高高度和不同倾斜角时毛细升高的长度和速度。

试验中将多孔陶瓷管底部放于水槽中，水刚好没过底部。由于毛细力作用，水份从底部往上升，直至达到一定高度［4］。吸水后的含湿陶瓷管在很多地方得到应用，如将其应用在被动蒸发冷却墙中，作为墙体的主体结构。通过含湿陶瓷管的热风促使陶瓷管表面水分蒸发，降低表面温度，从而冷却热风，为人们提供一个舒适的环境，有利于缓和现代社会愈演愈烈的城市热岛效应。

实验研究对象为由硅藻土烧结而成多孔陶瓷管，使用挤出型工艺制作。具体参数如下：材料：硅藻土（主要成分为SiO2），烧制温度：1250℃，外径：6.70 cm，内径：4.47 cm，陶瓷管高度：50 mm，抗压强度：23 N。

在实验中以下实验仪器将会被使用：

（1）电子天平。型号为JS系列，使用温度应在5～35℃，相对湿度为50%～80%。

（2）电热鼓风干燥箱。型号为101-3A，使用环境为控制温度范围为10～250℃，温度波动为1℃，工作环境温度为5～40℃。

（3）热成像仪。型号为FLLIKE-VT02。

（4）扫描电子显微镜。型号为KYKYEM6000，使用环境为16～25℃，相对湿度小于70%，地板负荷大于246 kg/㎡ 。

（5）游标卡尺。型号为SANTO 8012。

4.1多孔陶瓷管孔隙率的测量

多孔陶瓷管孔隙率指的是陶瓷管内部开口孔隙的体积和陶瓷管总体积的比值。基于气体膨胀法原理的吸渗法，在试验中，首先对多孔陶瓷管进行表面处理，清理表面易掉的硅藻土颗粒。随后放入干燥箱中进行除湿处理，干燥箱温度设定为150℃。待3 h后取出多孔陶瓷管称重并记录，4 h时再次取出并记录，如此每隔1 h测量1次，直至质量不发生变化。重复以上操作3次，取平均后的数据便是陶瓷管完全干燥时的质量。待多孔陶瓷管冷却至环境温度，把多孔陶瓷管放入水槽中，使其完全浸没。5 d后取出，待其表面没有明显液滴时称重并记录，以后每0.5 d重复此操作。待数值不发生变化时，此时的质量便是多孔陶瓷管完全水饱和时的重量。

图6　浸泡中的陶瓷管

图7　多孔陶瓷管内径外径测量图

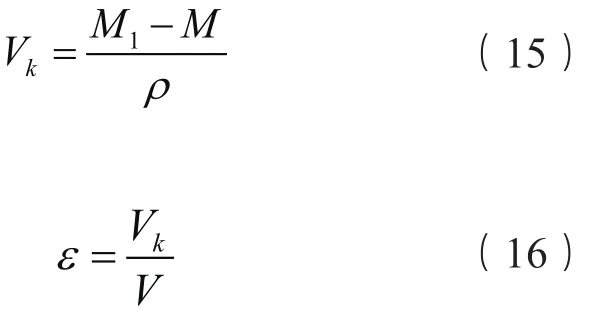
式中，Vk为要测量的孔隙体积，M1为孔隙内充满水之后的多孔介质的质量，M为完全干燥情况下多孔介质的质量，ε为多孔介质孔隙率，V为干饱和状态下的多孔介质体积。

由于实验所用多孔陶瓷管为规则体，可以使用数学方法计算其体积。使用游标卡尺从三个角度分别测量陶瓷管的内外径，分别进行平均可得出陶瓷管的内径和外径，使用米尺测量多孔陶瓷管的竖直高度。根据式（17）算出多孔陶瓷管的体积。

式中rw为陶瓷管外径，rn为陶瓷管内径，l为瓷管竖直高度。

根据实验测量可知多孔陶瓷管的体积为0.000188 m³，陶瓷管的干重为871.57 g，完全饱和的陶瓷管重量为1 454.25 g。根据式（15）、（16）可得实验所用的多孔陶瓷管孔隙率为0.31。

4.2多孔陶瓷管孔径的测量

由于多孔陶瓷管孔径与颗粒直径很小，使用一般的设备不易测量，故使用扫描电子显微镜测量，如图8。

首先从所使用的陶瓷管上获得一小块碎片，处理成1 cm×1 cm×1 cm大小的实验样本，清理实验样本表面，对实验样本进行蒸镀导电层处理和真空处理，后进入样本观察阶段。然后取出样品，此时注意样品室高压卸去，样品台归位，通过送样杆取回样本。

使用扫描电子显微镜对多孔陶瓷管试样进行扫描拍照，并标记孔径尺寸，如图9所示。由图9可得，多孔陶瓷管内部有许多不规则的孔径，其直径5 至14 不等，其中5 大小的孔径占多数。

图8　扫描电子显微镜

4.3多孔陶瓷管毛细升高的测量

本实验采用铅垂把米尺固定在陶瓷管上，以便读取数据。将一根陶瓷管竖直、另一根倾斜30°放入底面尺寸为20 cm×20 cm的长方体水槽，记录初始液面高度，后每5 min读取1次数据，实验延续4 h停止。后将陶瓷管进行干燥，取出后使后者再倾斜20°，快速使水槽内充满水，并读取初始液位高度，后每5 min读取一次数据，实验延续4 h停止。则分别测量竖直、60°、40°3种情况下不同时间的毛细升高高度，如图10所示。

图10　陶瓷管处于不同倾斜角时的实验图

图11　不同倾斜角时毛细升高长度图

从图11中可知，当陶瓷管竖直时，液位随时间逐渐升高，此时毛细升高最高时已达到35 cm，且没有停止增长，但其毛细升高速度逐渐减慢，最终液位将停在某一固定高度。原因分析：在毛细水上升的初始阶段，距水面较近处的孔隙接近饱和状态，而较大的含水率所产生的毛细上升阻力较大，其对毛细上升力的消减作用比较明显，因此上升速度衰减显著；随着毛细水上升高度增加，黏性阻力和重力已平衡掉很大部分毛细上升力，孔隙中毛细水含量变得很少，消减作用也变得很弱，因此上升后期速度缓慢且持久。实验中竖直放置时的毛细升高走势与模拟结果较吻合。

此外，不同倾斜角情况下毛细升高的高度均为随时间逐渐升高，但速度逐渐减慢。当处于同一时刻时，毛细升高速度和长度从高至低依次为倾斜角为40°、60°、竖直状态。且容易发现，在实验初期，3种不同倾斜角情况下毛细升高的长度相近。实验中3种倾斜角毛细升高高度的对比与模拟结果符合。

5　结论

主要分析了多孔介质孔隙内为气液两相时的湿份迁移机理，提出了基于液相饱和度的湿份迁移数学模型和计算方法。分别从不同颗粒直径、不同饱和度、不同倾斜角三个方面比较了多孔介质毛细升高高度随时间变化的情况。后以多孔陶瓷管为实验对象，进行了实验验证。得出以下结论。

（1）多孔介质液位迁移的最终高度与多孔介质材料颗粒有关，当工质为水时，颗粒直径越小，毛细升高的最终高度越高。但在初期，毛细升高的速度随着颗粒直径的减小而加快。

（2）在液相连续能够移动的范围内，随着饱和度的降低，毛细升高的速度和最终高度都依次升高。

（3）多孔介质倾斜角影响毛细升高的长度。随着倾斜角的减小，毛细升高的长度逐渐增大。但实验初期其上升长度基本相同。

参考文献

［1］陈威，刘颂，林俊.汲液式多孔介质应用于被动蒸发制冷墙的性能分析［J］.建筑科学，2014：15

［2］N.Fries，M.Dreyer.An analytic solution of capillary rise restrained by gravity［J］.Journal of Colloid and Interface Science，320（2008）259-263

［3］黄晓明.多孔介质相变传热与流动及其若干应用研究［M］.武汉华中科技大学

［4］Ibrahim E，Shao L，Rifat S b.Performance of porous ceramic evaporators for building cooling application［J］.Energing an Building，2003（35）：941-949

Research on Porous Medium Capillary Rising Characteristic

Chen Wei，Ling Juanjuan，Zhao Qunli
Shanghai Maritime University Merchant Marine Academy

Abstract：On the basis of gravity，the article tries to do research on capillary rising characteristic inside porous medium under unsaturated liquid phase condition.It also establishes mathematical model to calculate function relation between capillary rising height and time.It takes an example of porous ceramic tube to verify model correctness and analyze influence factors of capillary rising height changes.The results show that smaller particles diameter is，higher capillary rising height is.During liquid flow range，lower saturation degree is，higher capillary rising height is.Besides porous medium inclination angle degree would have an impact on capillary rising height，but initial length is the same.

Key words：Porous Medium，Capillary Rising，Particle Diameter，Saturation Degree

基金项目：国家自然科学基金（51276107）；上海市教委创新科研课题（14ZZ142）；交通部应用基础项目（2013319810150）

DOI：10.13770/j.cnki.issn2095-705x.2016.04.006

［作者简介］