基于文丘里流量传感器的湿气两相流量模型研究

徐　英，蒋　荣，张　涛，袁　超，陈吴晓，吴海涛

(天津大学 电气与自动化工程学院，天津 300072)

研究与探讨

基于文丘里流量传感器的湿气两相流量模型研究

徐英，蒋荣，张涛，袁超，陈吴晓，吴海涛

(天津大学 电气与自动化工程学院，天津 300072)

摘要:研究旨在通过计算流体动力学(CFD)仿真技术预测的湿气气、液两相流量。以双差压长喉颈文丘里流量传感器为测量手段。模拟压力范围0.4，0.6，0.8，1.0，1.2 MPa，气相体积流量范围为140～283 m3/h，温度范围23～30 ℃，含液率范围0.5 %～1.5 %。文丘里流量传感器口径为DN100，节流比为0.55。多相流模型采用离散相模型(DPM)，利用欧拉壁面(EWF)模型以模拟管壁上的薄液膜。分析得出压力、气相流速和液相体积含率(LVF)对液膜厚度的影响规律。根据仿真结果建立基于双差压比值法的气、液两相流量预测模型。将仿真值与实验值进行比较，气相流量模型预测的均方根误差为1.8 %，且液相流量模型预测的均方根误差为6.1 %。

关键词：长喉颈文丘里；湿气；环雾状流；欧拉壁面模型；差压比；液膜厚度

0引言

湿气作为一种特殊形式的气液两相流，常见于天然气的开采与测量等工业过程中。2012年的国际标准ISO/TR11583:2012技术报告[1]将其定义为“气相体积含率(gas volume fraction,GVF)大于95 %的气液两相流”。

差压式流量计通过测得的差压信号实现对流体流量的测量，然而用其测量湿气时则会出现“虚高”现象，即产生的差压信号会高于等量干气单独流过时产生的差压信号。因此,为了得到真实的气相流量，自然需要对虚高进行修正。为此,国内外学者针对不同的影响因素提出了诸多虚高修正模型，其中有着广泛影响力的有Homogenous模型、Murdock模型、Chisholm模型、Lin模型、De Leeuw模型、Steven模型和Reader-Harris模型等。

以上经典模型通常基于不同结构的节流式装置，均有一定的理论基础与大量的实验数据作为支撑，在一定的实验条件下具有精度高、重复性好等优点。然而是否具有良好的外推性，往往需要使用者进一步验证。本研究针对D=100 mm,β=0.55的长喉颈文丘里，实验介质为空气和水，实验装置为双闭环可调压中压湿气实验装置，其工作原理详见文献[2]，且针对环雾状流进行仿真。对于环雾状流中的液相，一部分以液膜形式存在，由于气液交界面的剪切力作用，其运动会呈现波动状态[3]；一部分以雾状液滴形式存在，受气相夹带的影响，被卷吸至气核中并随着气核流动[4]。因此，环雾状流具有环状、雾状、分层、波动等多重特征，最具代表性,同时也是最具仿真难度的一种流型。因此,本文提出了针对环雾状流的仿真方法，并给出了基于长喉颈文丘里流量传感器的气、液两相流预测模型。

1仿真工况条件

仿真方案见表1。对低压条件下的气、液两相流量进行仿真预测，根据贝克流型图[5]的预测，该工况条件下的湿气流型主要分布在环状流和波状流区域，如下图1所示。图中虚线是环状流与雾状流的分界线，但通常环状流不会突变为雾状流，而是在一定范围内两种流态共存，即一部分液相以液膜形式存在，一部分则为夹带在气相中的雾状液滴。因此,本文针对环雾状流进行仿真与分析。

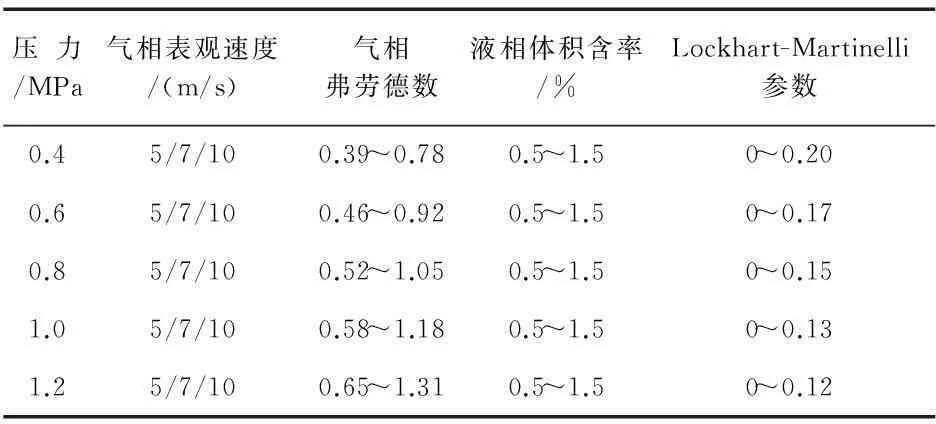
表1　仿真方案

其中，气相表观速度Usg、气相弗劳德数Frg、液相体积含率(LVF)和Lockhart-Martinelli参数XLM的表达式如下

(1)

(2)

(3)

(4)

式中g为重力加速度，Ql,Qg分别为液相和气相体积流量，Qmg为气相质量流量，ρg,ρl分别为气相和液相密度。

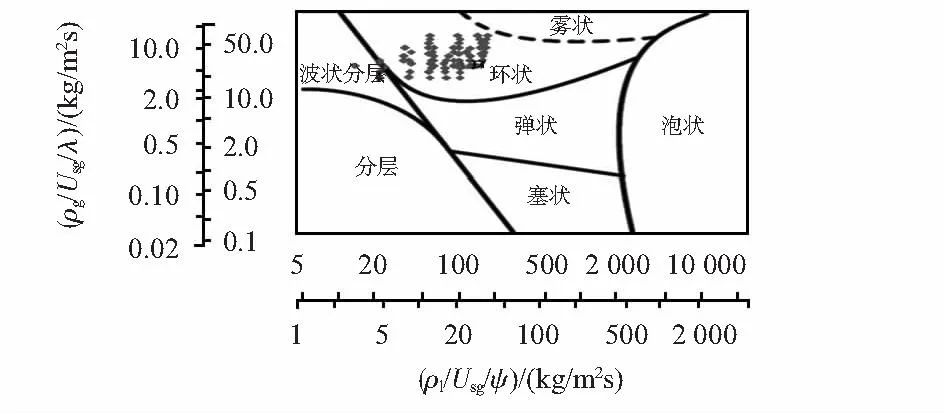
图1　湿气流型预测Fig 1　Prediction of wet gas flow pattern

2离散相模型

本文中涉及的仿真工况均为LVF小于等于1.5 %的情况，液相相对于气相而言很稀薄。根据文献[6]，本文将液相视为离散相颗粒，气相为连续相，考虑到离散相的分布与连续相流场之间的相互作用，而采用相间耦合计算方法，通过交替迭代计算连续相和离散相直到两相的计算结果都达到收敛标准。

2.1液滴轨道计算

在仿真计算过程中，通过积分拉式坐标系下的颗粒作用力微分方程来求解离散相颗粒(即液滴)的轨道。颗粒的作用力平衡方程在笛卡尔坐标系下的形式(x方向)为

(5)

式中Fs为Saffman升力，FD(ug-up)为液滴的单位质量曳力，其表达式为

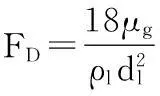
(6)

式中ug为气相速度，up为液滴速度，μg为气相动力粘度，dp为液滴直径，CD为曳力系数，Re为相对雷诺数(液滴雷诺数)。

2.2液滴粒径分布

粒径是液滴的特征参数，它决定了气相和液相两相间的曳力大小。综合考虑有效性和实用性两个因素时，Rosin-Rammler(RR)液滴粒径分布函数便成为了相对较好的选择[7]。该分布函数的表达式为

(7)

式中d为颗粒直径，d-为颗粒平均直径，n为分布指数，Yd表示大于直径d的颗粒所占的质量分数。本文将最小粒径为50 μm，最大粒径为800 μm，平均粒径为400 μm。

2.3欧拉壁面液膜模型

在仿真过程中,选用欧拉壁面液膜(Eulerian wall film，EWF)模型如图2所示，旨在解决薄液膜流动的问题。因EWF模型能预测液滴在管道壁面上的各种物理状态，包括液体的飞溅、颗粒成带状、液膜在管道壁面边缘分离，该模型还能预测薄液膜在壁面上的流动状态。

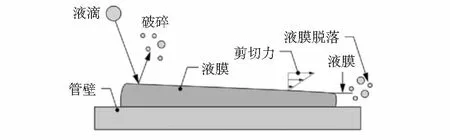
图2　EWF模型Fig 2　EWF model

在三维计算域中，二维液膜的质量守恒方程为

(8)

液膜的动量守恒方程为

(9)

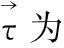
3仿真方法

3.1几何建模与网格划分

长喉径文丘里仿真模型的几何结构如图3所示。其直管段直径D=100 mm，节流比β(文丘里喉部直径与管径之比)为0.55，前后直管段长度均为10D。设定3个取压位置，前取压点P1距离收缩段入口50 mm，喉部取压点P2距离喉部入口为165 mm，为时流体流动充分发展[8],后取压点P3距离文丘里扩张段出口6倍管径，即600 mm。网格模型采用质量较高的结构化三维六面体网格，网格总数在1 000 000左右。

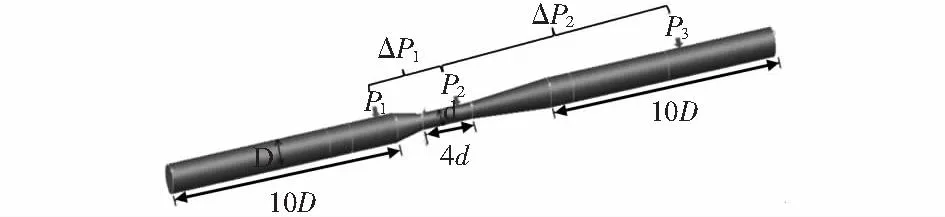
图3　DN100，β=0.55长喉颈文丘里模型Fig 3　Long-throat Venturi model for DN100,β=0.55

3.2仿真计算流程

在对湿气进行仿真时，本文选定重整化群(re-normalization group,RNG)k-e湍流模型[9]，运用Fluent中提供的DPM模型、离散相随机轨道(discrete random walk,DRW)模型和EWF模型，具体数值计算流程如图4所示。

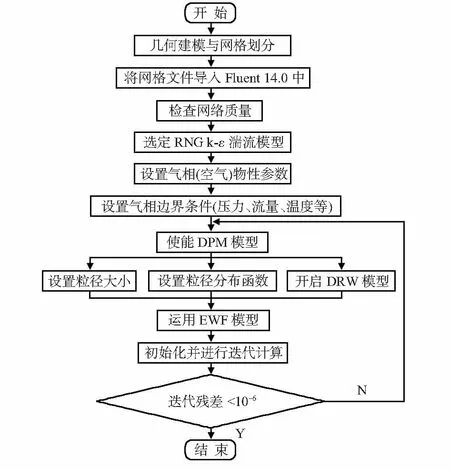
图4　数值计算流程图Fig 4　Flow chart of numerical calculation

4结果与讨论

4.1液相浓度分析

图5所示为湿气流经长喉颈文丘里管时各横截面上液相浓度分布情况。以LVF=1.0 %为例，从图中可以看出，在文丘里上游取压位置附近湿气以环雾状流的形式分布在管道横截面上；当液相流经文丘里收缩段时，由于流动面积的减小，液相浓度会相对变大并有向管道中心汇聚的趋势；在文丘里喉部，液相逐渐向管道中心汇聚，形成“环状射流”，管壁附近的液相浓度逐渐减小；在文丘里扩张管段，液相浓度在中心轴线位置达到最大；当流经下游直管段时，汇聚在中心轴线处的液相会逐渐向边壁扩散，管壁附近的液相浓度逐渐增加并趋于稳定。对于不同的液相体积含率，液相浓度沿x轴正向的变化规律相似，且液相浓度随LVF的增大而增大。

图5　文丘里管内液相浓度分布图(p=0.8 MPa，Usg=7 m/s)Fig 5　Liquid phase concentration distribution in Venturi pipe

4.2液膜厚度仿真结果

液膜在管壁上的分布如图6所示。在上游管段，尤其在流体流经收缩段之前，壁面液膜厚度虽有小的波动，但较为平稳；在文丘里收缩段区域，由于气相对液相有加速作用，液相会以液滴的形式夹带于气核中，导致液相壁面液膜厚度沿轴向急剧下降并在文丘里喉部入口处达到最薄；在文丘里喉部，液膜厚度略有增大且变化较为平缓；在扩张管段，气相湍流对液相的扩散作用，导致液膜厚度波动剧烈但总体呈上升趋势；在文丘里下游直管段区域，液膜厚度趋于平稳且略低于上游管段的液膜厚度。

由图6可知，液膜厚度与压力、气相表观流速和液相体积含率均有关：观察图6(a)可知，同一气相流速和液相含率条件下，压力越大，气相和液相混合越均匀，故液相在壁面积聚量越少,液膜越薄；图6(b)表明，相同压力、液相含率时，气相流速越小，积聚在管壁处液膜越厚；分析图6(c)可知，相同压力、气相流速下，随着含液率的增加，液膜加厚。

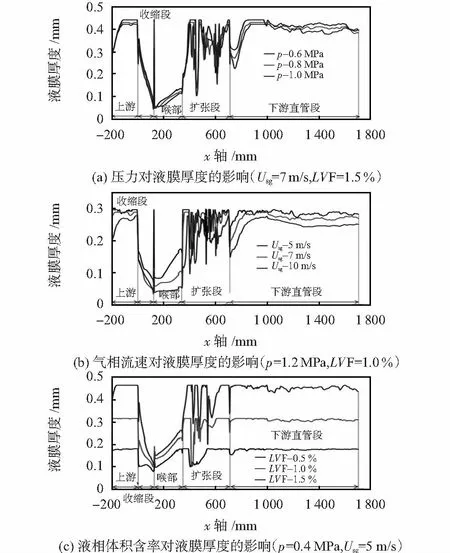
图6　管壁上液膜厚度分布情况Fig 6　Liquid film thickness distribution on pipe wall

4.3仿真预测模型

4.3.1气相虚高模型

研究表明，虚高φg与XLM参数[10]、Froude数和气液密度比等工况参数密切相关。而对于在线不分离测量XLM参数为未知值，借鉴文献[11]中的方法与结论，即引入无量纲参数—文丘里前差压Δp1与后差压Δp2的比值K，用以代替XLM，并建立如下气相虚高模型

(10)

式中a=0.797 3，b=-0.181 2，c=-0.140 6，d=-0.336 5，e=-0.120 7。气相模型的拟合误差为2.81 %。

4.3.2液相预测模型

无论是在实流实验测量还是在仿真计算的过程中，液相的存在是导致虚高现象的根本原因。因此，当已知虚高值时，便可以计算出液相质量流量。本研究中，为了获得液相预测模型，采用数据拟合的方式得出液气质量比与虚高值、Froude数三者之间的关系式为

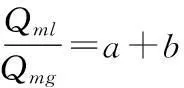
(11)

式中a=1.664 7，b=-4.894 3，c=3.334 7，d=-0.156 3，e=0.033 2。液相模型的拟合误差为4.8 %。

4.4气相与液相的预测结果

在对湿气进行仿真的过程中，当已知虚高值时，气相真实的质量流量计算公式如下

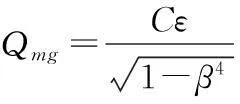
(12)

式中C为流出系数，ε为可膨胀系数。

利用4.3中得到的气相虚高预测模型和液相预测模型，便可以预测出气相质量流量和液相质量流量。图7(a)所示为气相质量流量的预测值与实流实验值对比后的相对误差。图7(b)所示为液相质量流量的预测值与实流实验值对比后相对误差。由图7(a)可知，仿真预测与实验的气相流量误差基本上均分布在-3.5 %～2 %的范围内。由图7(b)可知，仿真预测与实验的液相流量误差在-15 %～18 %的误差带内，其中液相误差在[-10 %，10 %]的置信区内的概率为88.4 %。

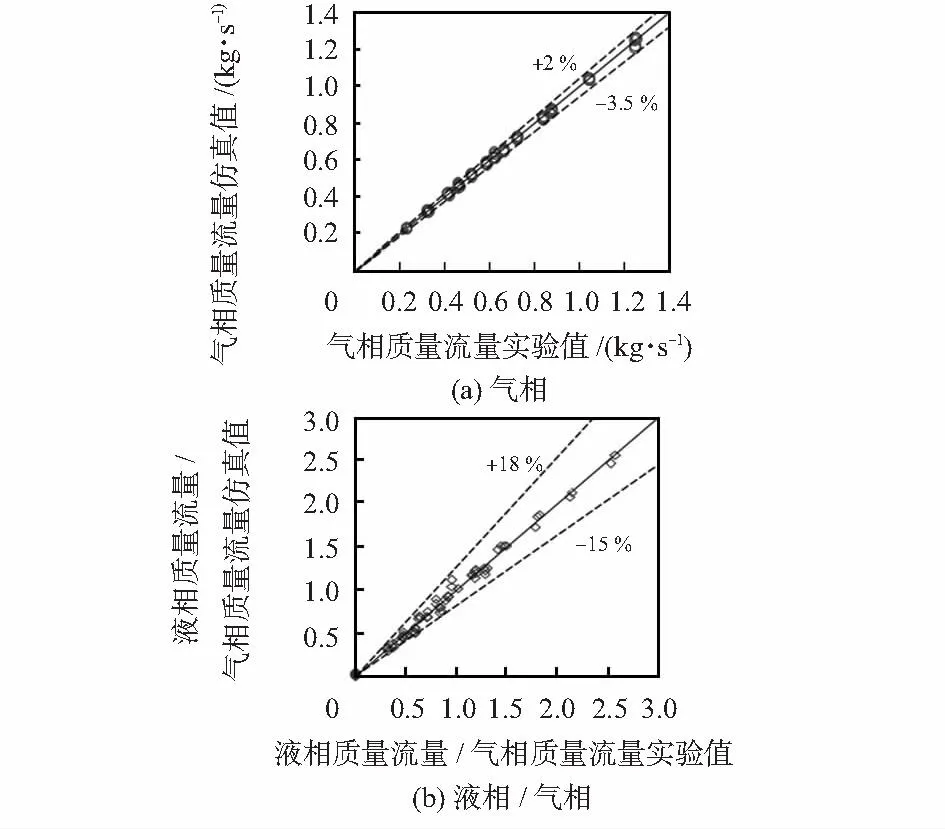
图7　仿真预测与实验质量流量的相对误差Fig 7　Relative error of mass flow of experiment and simulation prediction

5结论

本研究基于环状流理论模型，利用DPM和EWF仿真模型，对工况条件下的环雾状流进行数值计算，从而得到液相浓度分布情况、液膜厚度信息。对仿真计算得到的差压值进行拟合，最终得到气、液两相的流量预测模型。其中，气相模型预测的均方根误差为1.8 %，而液相模型预测的均方根误差为6.1 %。

参考文献:

[1]International Standard Organization.Technical report ISO/TR11583 measurement of wet gas flow by means of pressure differential devices inserted in circular cross-section conduits[S].Switzerland：2012.

[2]徐英,尹存,龙征海.可调压中压湿气实验装置的研制[J].天津大学学报，2014,47(1):47-53.

[3]李春曦,王松岭,叶学民.气液界面剪切力对液膜流动稳定性的影响[J].中国电机工程学报,2009,29(8):60-63.

[4]赵海波，郑楚光.离散系统动力学演变过程的颗粒群平衡模拟[M].北京:科学出版社，2008.

[5]阎昌琪.气液两相流[M].哈尔滨：哈尔滨工程大学出版社，2007.

[6]ANSYS Inc.ANSYS Fluent theory guide release 14.0[EB/OL].[2011—11—10].http:∥www.ansys.com,Southpointe.

[7]Mugele R A,Evans H D.Droplet size distributions in sprays[J].Ind Eng Chem,1951,43(6):1317-1324.

[8]郭素娜，孙立军，杨振,等.基于CFD仿真的切向涡轮流量传感器结构优化[J].传感器与微系统，2015,34(8):26-29.

[9]徐英,安俊达,龙征海，等.双锥流量传感器的数值模拟与优化设计[J].天津大学学报，2013，46(11)：984-990.

[10] Lochart R W,Martinelli R C.Proposed correlation of data for isothermal two-phase,two-component flow in pipes[J].Chemical Engineering Progress,1949,45:39-48.

[11] 张强,徐英,张涛.基于长喉颈文丘里管的双差压湿气流量测量[J].天津大学学报，2012，45(2)：147-153.

Research on two-phase flow model for wet gas based on Venturi flow sensor

XU Ying，JIANG Rong，ZHANG Tao，YUAN Chao，CHEN Wu-xiao，WU Hai-tao

(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

Abstract:A two-phase flow model for wet gas predicted by CFD is researched.This simulation aims at dual differential-pressure long-throat Venturi flow sensor.Simulation pressure ranges of 0.4～1.2 MPa,gas phase volume flow range of 140 m3/h～283 m3/h,temperature range of 23～30 ℃,liquid of volume fraction is range of 0.5～1.5 %.The diameter of Venturi flow meter is 100 mm and throttle ratio is 0.55.The multiphase flow model uses discrete phase model(DPM),Eulerian wall film(EWF)model is used to simulate thin liquid film on pipe wall.Influence rule of pressure/gas phase flow velocity and liquid volume fraction(LVF)on liquid film thickness can be found from analysis.Gas liquid flow prediction model are set up based on dual differential pressures ratio method according to simulation result.Compare simulation value and experimental value,it shows that root mean square error(RMSE)of gas flow model prediction is 1.8 %,and RMSE of liquid phase flow model prediction is 6.1 %.

Key words:long-throat Venturi;wet gas;annular-mist flow;Eulerian wall film(EWF)model;differential pressure ratio;liquid film thickness

DOI:10.13873/J.1000—9787(2016)05—0004—05

收稿日期：2015—09—24

中图分类号：TP 216

文献标识码：A

文章编号：1000—9787(2016)05—0004—05

作者简介:

徐英(1970-)，女，天津人，教授，博士生导师，主要从事湿气流量计量和智能化仪表的研发。