面向BRT车队形成的站台乘车诱导控制模型

卢　凯　 吴　焕　 张　孜　 徐广辉　 胡建伟

(1华南理工大学土木与交通学院, 广州 510640)(2东南大学现代城市交通技术协同创新中心, 南京 210096)(3广州市交通委员会, 广州 510620)

面向BRT车队形成的站台乘车诱导控制模型

卢凯1,2吴焕1张孜3徐广辉1胡建伟1

(1华南理工大学土木与交通学院, 广州 510640)(2东南大学现代城市交通技术协同创新中心, 南京 210096)(3广州市交通委员会, 广州 510620)

摘要:分析了乘客乘车诱导控制对公交车辆停站时间的影响．根据BRT站台内乘客的OD需求,利用站台乘车诱导控制方法,以BRT车辆进出站台保持队形为目的,建立了单条与多条公交线路车辆的停站时间模型．给出了停站时间状态方程的矩阵形式,分别设计了全局寻优的遍历方法和局部快速寻优的遗传算法,使得同一进站车队中不同公交车辆的停站时间趋于一致,从而实现了面向BRT车队形成的站台乘车诱导控制．通过案例分析,对比了利用本模型所求诱导控制方案与无诱导方式下客流均分方案的实施效果,验证了本模型在均衡公交站台车辆停站时间的优越性,为实现上下游交叉口间的BRT车队协调控制奠定了技术基础．

关键词:BRT;停站时间;乘车诱导;车队形成;公交站台;状态方程

当公交车队从上游信号交叉口驶出并到达公交站台后,如果各公交车辆的上下车乘客数相差较大,则会使得公交车辆在站台上的停站时间不相等,驶出站台时难以保持队形,不利于在下游交叉口对公交车辆实施信号协调控制．因此如何通过合理的乘客分配,使得公交车辆驶出站台时仍能保持队形,是实现公交信号协调控制的重要前提．特别是对于BRT公交系统,由于不同线路之间存在较多的站点重合,且经过上游信号交叉口后车辆往往将以车队形式进入下游站台,因此可以针对即将进站的车队进行乘客选乘线路的合理分配,使得各进站车辆的停站时间均等,以保持公交车辆驶出站台时的队形,从而有利于在下游信号交叉口对BRT车队进行信号协调控制．

20世纪80年代起,国内外学者开始对公交车辆停站时间展开研究．Levinson[1]统计发现停站时间主要由乘客上下车时间和车门开闭时间决定;Guenthner等[2]研究了公交车辆停站时间与公交收费系统之间的关系;Jiang等[3]研究了不同公交站台类型下乘客特性对公交车辆停站时间的影响,建立了公交车辆停站时间回归模型;Milkovits[4]研究了上下车乘客数、收费形式、车辆设计等因素对停站时间的影响;Meng等[5]提出了一种基于概率的停站时间估计方法;Gonzalez等[6]建立了城市公交主线上的停站时间模型;Zhang等[7]针对上海市的公交现状,综合考虑上下车人数、拥挤度、收费方式等因素影响,建立了较为精确的公交停站时间预测模型;彭庆艳等[8]建立了公共汽车中途站停靠时间模型;吴洋等[9]建立了乘客上下车时间的统计与回归模型;陈耀如[10]建立了公交车辆停站时间预测模型,提出了基于公交乘客总等待时间最短的泊位动态分配算法;邵敏华等[11]建立了车内拥挤程度与时间价值的函数关系,构建了乘客对车内拥挤的感知阻抗模型;钱臻等[12]考虑乘客上下车、步行、换乘、线路票价等因素影响,改进了现有的公交网络客流分配算法．

然而,现有文献对于乘客乘车的诱导控制方法[13]涉及甚少,没有从公交区间段的角度来考虑如何通过诱导技术均衡站台上各线路车辆的停站时间．因此，本文将引入一种BRT站台乘客乘车诱导的控制方法,以BRT区间段内车辆停站时间均衡为目的,建立一个面向BRT车队形成的站台乘车诱导控制模型,以保持公交车辆驶出站台时的紧凑队形．

1停站时间控制模型

车辆在公交站台的停站时间,通常由车辆基本停靠时间(正常进站停车、离站启动与车门开闭的时间和)和站台乘客上下车时间两部分组成．其中,对于站台乘客上下车时间的计算,将视站台乘客实际上下车过程而定．例如在一个公交系统中,若乘客通过刷卡进站,当公交车辆到站时,车内乘客将通过前后门同时下车,之后站台乘客再通过前后门同时上车,此时站台乘客上下车时间等于乘客上车时间与乘客下车时间之和;若乘客是在前门刷卡上车、后门下车,此时站台乘客上下车时间则取为乘客上车时间与乘客下车时间之中的较大值．本文的研究对象为BRT车辆,乘客上下车时间的计算采用求和方法．

为了阐明公交车辆停站时间的诱导控制原理及意义,下文将通过一个例子进行说明．

1.1问题分析

假设在某个BRT区段内包含2条公交线路(记为线1、线2)和4个公交站点(记为站1、站2、站3、站4)．其中线1在4个站点均有停靠,线2只在站1～站3有停靠;站1→站2、站1→站3的乘客数均为16人,站2→站3的乘客数为2人,站2→站4的乘客数为18人．已知乘客上车或下车平均所需时间均为1 s;线1与线2在到达站1前的车上初始载客中,均有5人在站1下车、3人在站2下车．

针对无诱导与有诱导2种情况,对比分析线1与线2公交车辆在站1和站2的停站时间.

1) 无诱导情况. 站台乘客的选乘规则为:乘客等概率地选乘可选线路,即乘客人数将被均分到各条可选公交线路上．分析无诱导时乘客选乘与车辆停站时间情况,结果如表1所示．由表可看出,线1与线2在站2的停站时间分别为30和12 s,由于停站时间相差较大,故难以继续保持车队．

表1　无诱导时乘客选乘与车辆停站时间情况

2) 有诱导情况. 站台乘客的选乘规则为:所有乘客均按照诱导方案选乘可选线路．对于诱导方案“在站1,诱导所有前往站2的乘客选乘线2,诱导所有前往站3的乘客选乘线1;在站2,诱导所有前往站3的乘客选乘线2,所有前往站4的乘客只能选乘线1”,分析有诱导时乘客选乘与车辆停站时间情况,结果如表2所示．由表可看出,线1与线2在站1和站2的停站时间都相等,故公交车队可以一直保持队形．

表2　有诱导时乘客选乘与车辆停站时间情况

根据公交站点之间的乘客OD需求,假设站台乘客均服从诱导控制,可以建立单条线路以及整个区段内的公交车辆停站时间控制模型．

1.2单条线路

1.2.1状态方程

对于一段包含n个站点的BRT区间段,以从第1站驶入到第n站驶出的公交线路i为例,建立该线路车辆在各公交站点的停站时间状态方程:

T(i,1)=t0+(u(i,1,2)q(1,2)+u(i,1,3)q(1,3)+

u(i,1,4)q(1,4)+…+u(i,1,n)q(1,n)+

u(i,1,n+)q(1,n+))t1+o(i,1)t2

T(i,2)=t0+(u(i,2,3)q(2,3)+u(i,2,4)q(2,4)+

u(i,2,5)q(2,5)+…+u(i,2,n)q(2,n)+

u(i,2,n+)q(2,n+))t1+(o(i,2)+u(i,1,2)q(1,2))t2

T(i,3)=t0+(u(i,3,4)q(3,4)+u(i,3,5)q(3,5)+

u(i,3,6)q(3,6)+…+u(i,3,n)q(3,n)+

u(i,3,n+)q(3,n+))t1+(o(i,3)+

u(i,1,3)q(1,3)+u(i,2,3)q(2,3))t2

⋮

T(i,n-1)=t0+(u(i,n-1,n)q(n-1,n)+

u(i,n-1,n+)q(n-1,n+))t1+(o(i,n-1)+

u(i,1,n-1)q(1,n-1)+u(i,2,n-1)q(2,n-1)+…+

u(i,n-2,n-1)q(n-2,n-1))t2

T(i,n)=t0+u(i,n,n+)q(n,n+)t1+(o(i,n)+

u(i,1,n)q(1,n)+u(i,2,n)q(2,n)+…+

u(i,n-1,n)q(n-1,n))t2

(1)

式中,T(i,j)为第i条公交线路车辆在第j站的停站时间;t0为车辆基本停靠时间(假设各车辆取值相同);t1为乘客平均上车时间;t2为乘客平均下车时间;u(i,j,k)为指引从第j站出发在第k站驶出BRT区段的乘客搭乘第i条公交线路车辆的提示信号;u(i,j,k+)为指引从第j站出发在第k站驶出BRT区段的乘客搭乘第i条公交线路车辆的提示信号;q(j,k)为从第j站出发到第k站下车的乘客人数;q(j,k+)为从第j站出发在第k站驶出BRT区段的乘客人数;o(i,k)为第i条公交线路车辆在第k站下车的初始乘客人数;n为公交站点总数．

由式(1)可归纳出从第1站驶入到第n站驶出的第i条公交线路车辆在第z站的停站时间T(i,z):

(2)

对于从第j站驶入到第k站驶出的公交线路i,可归纳出其在第z站(j≤z≤k)的停站时间T(i,z):

(3)

1.2.2控制变量

为了增加乘车诱导的可控性,提示信号控制变量u(i,j,k)与u(i,j,k+)只能取值为1或0,即

(4)

式中,控制变量取1表示指引搭乘,取0则表示不指引搭乘．

1.2.3评价指标

为了使得同一进站车队中不同公交车辆的停站时间趋于一致,选取公交站台上所有线路车辆的停站时间标准差作为评价指标(对于不在该站停站的线路车辆,将不被纳入停站时间标准差的计算)．

对于所有线路车辆均在公交站点j停站的情形,计算站点j的停站时间标准差σj,计算公式如下:

(5)

1.3整个区段

1.3.1状态方程

由公交站台停站时间计算通式(3),可联立组成整个BRT区段站点停站时间的状态方程组．

1.3.2控制变量

在各个公交站点上,所有途经线路的控制变量u(i,j,k)与u(i,j,k+)将满足如下关系:

(6)

1.3.3目标函数

为了使得公交车辆在离开各公交站点时都能保持较好的队形,在此选取整个区段内各站点停站时间方差之和作为目标函数,即

(7)

1.4矩阵形式

为了描述与计算方便,将停站时间模型转化为矩阵形式．

1.4.1矩阵定义

对于从第1站驶入到第n站驶出的公交线路i,搭乘线路i的需求矩阵Qi定义如下:

(8)

令q(i,1), q(i,2),…,q(i,n)为矩阵Qi的第1,2,…,n行向量,q(i,l)可记为

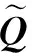
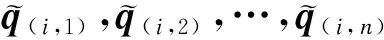
搭乘线路i的提示信号矩阵Ui定义如下:

(9)

令u(i,1), u(i,2), …,u(i,n)为矩阵Ui的第1,2,…,n行向量,u(i,l)可记为

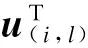
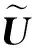
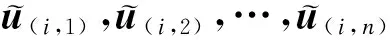
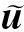
对于从第j站驶入到第k站驶出的公交线路i,搭乘线路i的需求矩阵Qi定义如下:

(10)

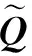
搭乘线路i的提示信号矩阵Ui定义如下:

(11)

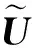
1.4.2矩阵方程

对于从第1站驶入到第n站驶出的公交线路i,建立如下停站时间矩阵方程式:

(12)

对于从第j站驶入到第k站驶出的公交线路i,建立如下停站时间矩阵方程式:

(13)

2模型求解

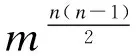
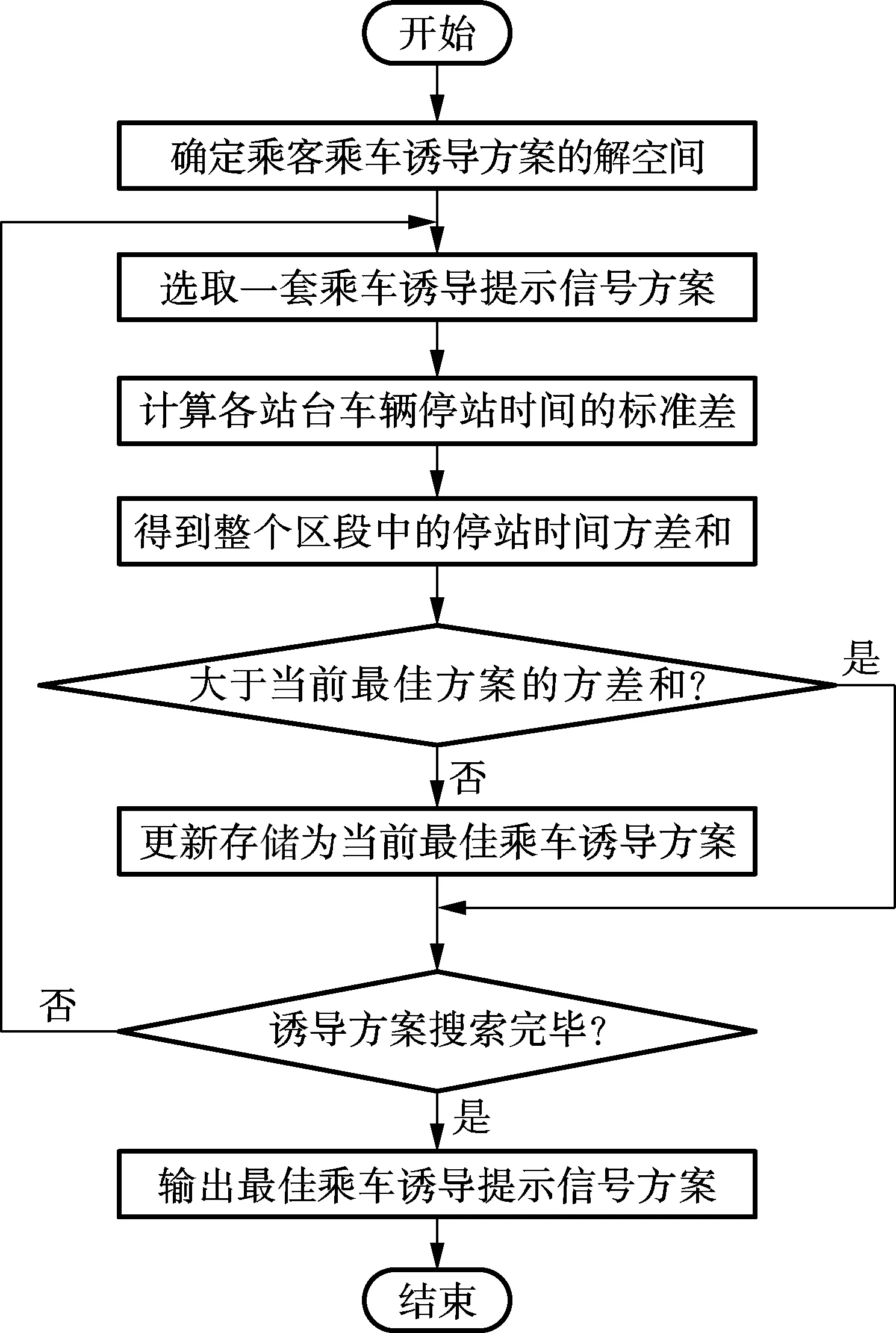
图1　遍历算法流程

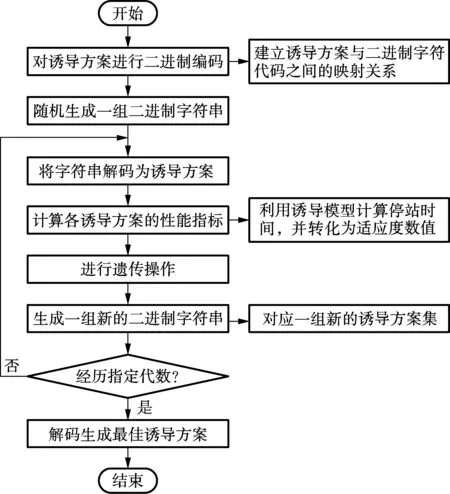
图2　遗传算法流程

使用遗传算法搜索最佳诱导方案时,需对任意一种乘客OD需求的选乘方案进行二进制编码和解码，即

r=sgn(log2t-[log2t])+[log2t]

(14)

(15)

式中,t为一种乘客OD需求所对应的可选乘线路总数;r为乘客可选乘线路数所对应的二进制编码位数;sgn为符号函数;[]为取整函数;(string)2为乘客OD诱导方案所对应的二进制码;a为可选乘线路最小编号;b为可选乘线路最大编号;s为所选线路序号．

3案例分析

已知某BRT区段内包含4个公交站点(S1～S4),有4条公交线路(L1～L4)在该区段内运行,各条线路在公交区段内的出入情况如表3所示．所有公交线路车辆的额定载客量均为80人,t0=10s,平均乘客上下车时间t1=1s,t2=1s．

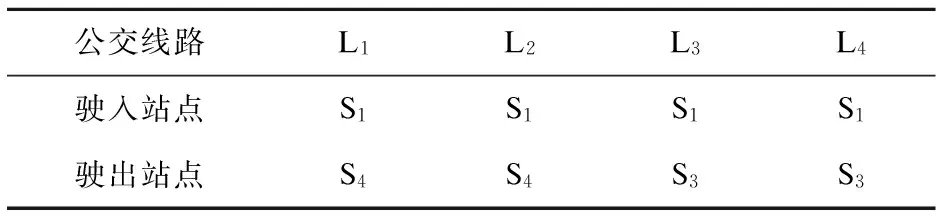
表3　各条线路在公交区段内的出入情况

已知公交站点之间的乘客OD需求,如表4所示．各线路车辆在中途各站下车的初始乘客人数,如表5所示．

表4　公交站点之间的乘客OD需求　人

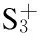
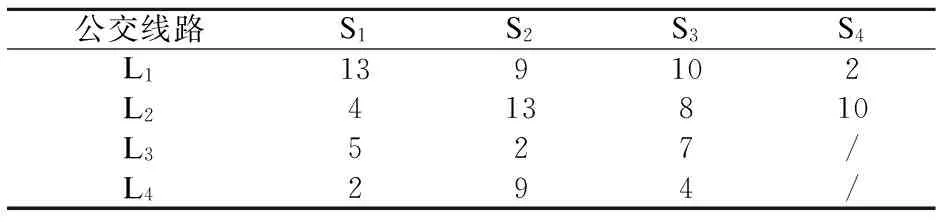
表5　中途各站下车的初始乘客人数　人

注:/表示该线路不在对应站点停靠,没有下车人数．

3.1模型建立

将表4和表5中的数据代入通式(3),分别建立各线路车辆在各站点的停站时间数学模型．各线路车辆的控制变量满足式(6)．

根据各站点的上下乘客数量与停站公交线路数目,可预先计算出各站点的平均停站时间:

各站点的停站时间标准差分别为

根据表4和表5中的数据,可利用式(13)建立停站时间矩阵方程，然后对其进行计算求解．

3.2计算分析

由于本例中乘车诱导提示方案数量有限(共65 536个),因此可以利用遍历算法对所有乘车诱导提示方案进行计算求解．运算环境为Inter(R)Core(TM)i5-3230MCPU@ 2.60GHz,内存为12GB,运算时间为2.1s．得到最优方案的目标函数值为23.63,最大标准差为3.49.最佳乘车诱导方案的提示信号矩阵U1～U4如下:

根据以上最佳提示信号矩阵,可计算出各线路车辆在各个站点的停站时间,如表6所示．

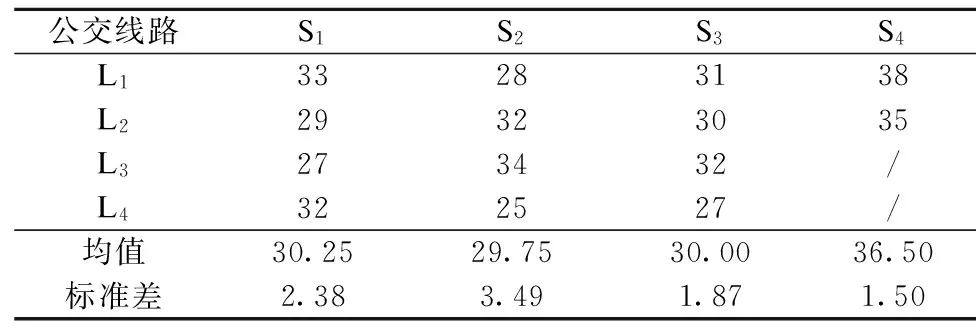
表6　各车辆在各站点的停站时间　s

注:/表示该线路不在对应站点停靠,没有停站时间．

由表6可看出,最佳乘车诱导提示方案使各站点上各车辆的停站时间较为接近,有利于站台驶出车辆保持队形．

3.3方案对比

在无诱导提示情况下,站台乘客等概率地选择可以到达目的地的公交线路,各站台的客流分配情况如表7所示．各线路在各站的上下车乘客数和停站时间如表8和表9所示．

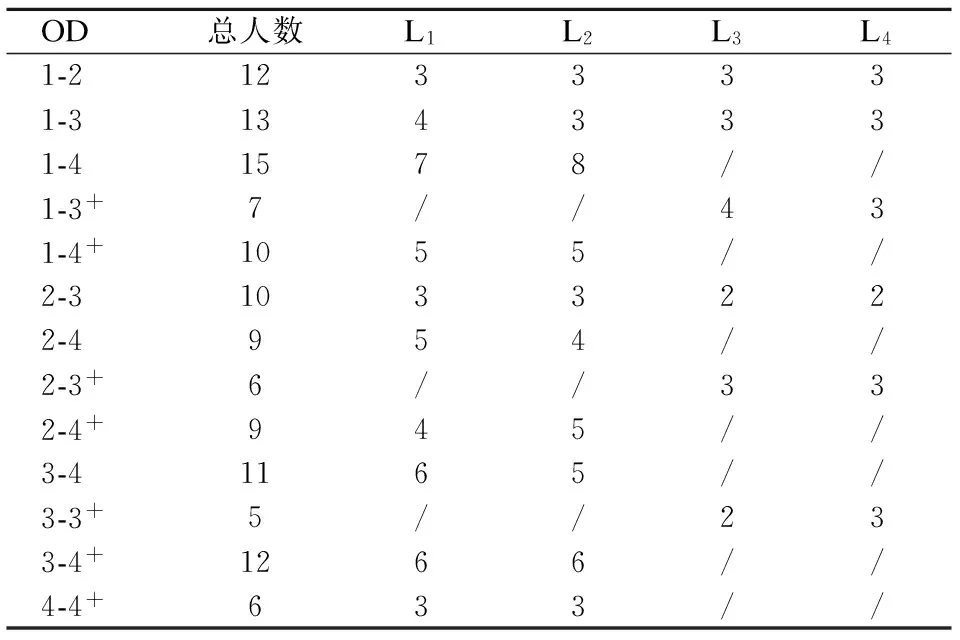
表7　无诱导提示情况下的客流分配　人

注:/表示该OD乘客不会选择乘坐对应线路．

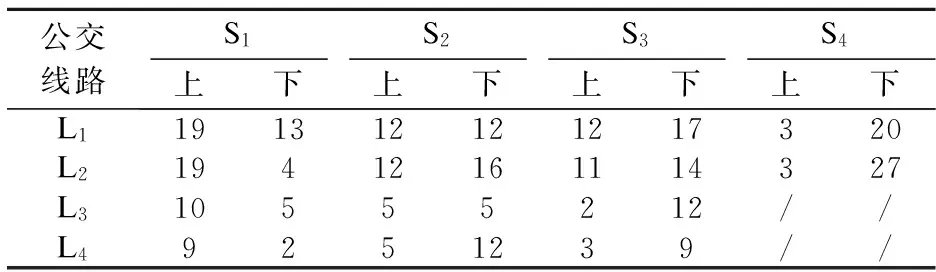
表8　无诱导提示情况下各站的上下车乘客数　人

注:/表示该线路不在对应站点停靠,没有上、下车人数．

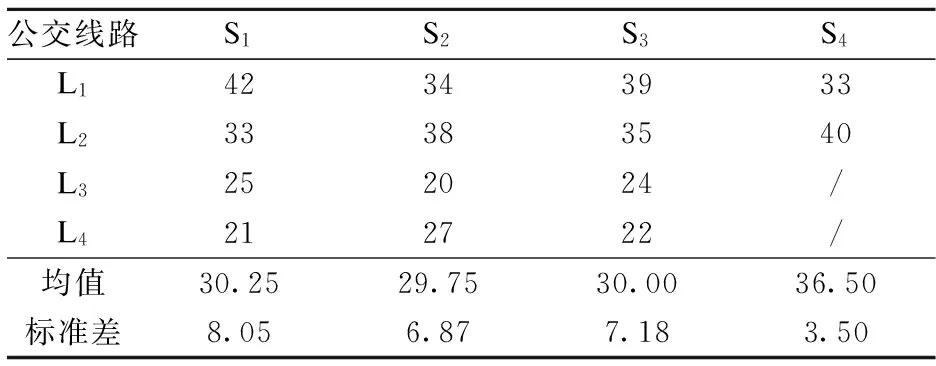
表9　无诱导提示情况下各线路在各站的停站时间　s

注:/表示该线路不在对应站点停靠,没有停站时间．

在无诱导提示情况下,各站停站时间方差之和为176.15,最大标准差为8.05．

对比表6与表9可看出,本文模型所求诱导方案在均衡公交车辆停站时间方面优越性显著．与无诱导提示方式相比,本文模型所求诱导方案的各站点停站时间方差之和降低了86.59%,最大站点停站时间标准差降低了56.65%,非常有利于保持BRT车辆进出站的队形．

4结论

1) 通过对乘客选乘车辆进行诱导指引,实现了对公交车辆停站时间的有效控制,从而可以使得进出站台的BRT车队保持队形．

2) 本文建立的停站时间控制模型,对BRT区间段内各站点的乘客上下车情况进行了综合考虑,所生成的诱导控制方案可以保证整个公交区间段全局最优．

3) 针对BRT区间段内站点与线路数量的不同情况,分别设计了遍历算法与遗传算法的求解流程,后者可以实现大规模方案下诱导控制方案的快速寻优．

本文提出的乘客乘车诱导方法是对BRT站台内每一种乘客OD需求进行统一性诱导,即诱导控制变量u只能取0或1．以后的研究目标是如何针对每一位乘客进行个性化诱导,使诱导控制变量u能在[0,1]上多样化取值,实现对乘客乘车的实时动态诱导控制．

参考文献 (References)

[1]Levinson H S. Analyzing transit travel time performance [J].TransportationResearchRecord, 1983, 915: 1-6.

[2]Guenthner R P, Hamat K. Transit dwell time under complex fare structure [J].JournalofTransportationEngineering, 1988, 114(3): 367-379.

[3]Jiang X K, Yang X G. Regression-based models for bus dwell time [C]//17thInternationalIEEEConferenceonIntelligentTransportationSystems. Qingdao, China, 2014: 2858-2863. DOI:10.1109/itsc.2014.6958148.

[4]Milkovits M. Modeling the factors affecting bus stop dwell time: Use of automatic passenger counting, automatic fare counting, and automatic vehicle location data[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2008, 2072:125-130. DOI:10.3141/2072-13.

[5]Meng Q, Qu X. Bus dwell time estimation at bus bays: A probabilistic approach[J].TransportationResearchPartC:EmergingTechnologies, 2013, 36:61-71. DOI:10.1016/j.trc.2013.08.007.

[6]Gonzalez E M, Romana M G, Alvaro O M. Bus dwell-time model of main urban route stops: Case study in Madrid, Spain[J].TransportationResearchRecord, 2012, 2274: 126-134. DOI:10.3141/2274-14.

[7]Zhang C, Teng J. Bus dwell time estimation and prediction: A study case in Shanghai-China[C]//13thCOTAInternationalConferenceofTransportationProfessionals. Shenzhen, China, 2013: 1329-1340.

[8]彭庆艳, 杨东援. 公共汽车中途站停靠时间模型[J]. 长安大学学报(自然科学版), 2002, 22(1):60-62.DOI:10.3321/j.issn:1671-8879.2002.01.016.

Peng Qingyan, Yang Dongyuan. Mathematical model of the dwell time at the bus stop[J].JournalofChang’anUniversity(NaturalScienceEdition), 2002, 22(1):60-62. DOI:10.3321/j.issn:1671-8879.2002.01.016. (in Chinese)

[9]吴洋, 罗霞. 公交车辆站停时间与乘客行为的关系[J]. 西南交通大学学报, 2007, 42(2):243-248.DOI:10.3969/j.issn.0258-2724.2007.02.022.

Wu Yang, Luo Xia. Relationship between bus stoppage time and passenger behavior[J].JournalofSouthwestJiaotongUniversity, 2007, 42(2): 243-248. DOI:10.3969/j.issn.0258-2724.2007.02.022.(in Chinese).

[10]陈耀如. 公交站台多停靠位乘客组织与智能引导[D]. 济南:山东大学控制科学与工程学院, 2014.

[11]邵敏华, 李田野, 孙立军. 常规公交乘客对车内拥挤感知阻抗调查与建模[J]. 同济大学学报(自然科学版), 2012, 40(7): 1031-1034. DOI:10.3969/j.issn. 0253-374x.2012.07.012.

Shao Minhua, Li Tianye, Sun Lijun. Survey method and model of passengers’ cost perception of crowding level in bus[J].JournalofTongjiUniversity(NaturalScience), 2012, 40(7):1031-1034. DOI:10.3969/j.issn.0253-374x.2012.07.012.(in Chinese)

[12]钱臻, 陆化普. 一种公交网络客流分配方法及其实用性研究[J]. 清华大学学报(自然科学版), 2005,45(9): 1170-1174.

Qian Zhen, Lu Huapu. An assignment method for transit network and its practical application[J].JournalofTsinghuaUniversity(ScienceandTechnology), 2005, 45(9): 1170-1174.(in Chinese)

[13]郑晓峰, 卢凯, 吴焕, 等. 基于BRT站台乘车诱导的公交车辆载客均衡模型[J]. 交通运输系统工程与信息, 2014, 14(3):137-141. DOI:10.3969/j.issn.1009-6744.2014.03.021.

Zheng Xiaofeng, Lu Kai, Wu Huan, et al. Bus passenger equilibrium model based on BRT station boarding guidance[J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2014, 14(3):137-141. DOI:10.3969/j.issn.1009-6744.2014.03.021.(in Chinese)

Bus station boarding guidance model oriented to BRT platoon formation

Lu Kai1,2Wu Huan1Zhang Zi3Xu Guanghui1Hu Jianwei1

(1School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China) (2Collaborative Innovation Center of Modern Urban Traffic Technologies, Southeast University, Nanjing 210096, China) (3Communications Commission of Guangzhou Municipality, Guangzhou 510620, China)

Abstract:The effects of passenger boarding guidance on bus dwell time are analyzed. According to the origin-destination(OD) demand of bus rapid transit (BRT) station passengers, the dwell time models for a single bus route and multiple bus routes are established, respectively, by the bus station boarding guidance. The models aim at maintaining the platoon of BRT when it goes through the bus station. The matrix of the dwell time state equation is put forward. The traversal algorithm for global optimum seeking and the genetic algorithm for local rapid optimum seeking are designed, respectively. Thus, the dwell time of different buses is uniform, and the bus station boarding guidance control oriented to the BRT platoon is realized. By case analysis, the implementation effects of the control scheme with the boarding guidance solved by the model are compared with the passenger flow equipartition scheme without boarding guidance. Therefore, the advantages of the model for balancing bus station dwell time are proved. The boarding guidance model provides a foundation for BRT platoon coordination control between upstream and downstream intersections.

Key words:bus rapid transit(BRT); dwell time; boarding guidance; platoon formation; bus station; state equation

DOI:10.3969/j.issn.1001-0505.2016.03.034

收稿日期:2015-11-23.

作者简介:卢凯(1979—),男, 博士, 副教授, kailu@scut.edu.cn.

基金项目:国家自然科学基金资助项目(61203164)、广东省科技计划资助项目(2015A030401024)、广州市珠江科技新星专项资助项目(2013J2200066)、广东省交通运输厅科技资助项目(2013-02-055)、中央高校基本科研业务费专项资金资助项目(2015ZZ073)、广州市南沙区科技计划资助项目(2014MS11).

中图分类号:U492.22

文献标志码:A

文章编号:1001-0505(2016)03-0657-07

引用本文: 卢凯,吴焕,张孜,等.面向BRT车队形成的站台乘车诱导控制模型[J].东南大学学报(自然科学版),2016,46(3):657-663. DOI:10.3969/j.issn.1001-0505.2016.03.034.