考虑参数不确定性的汽车前轮主动转向输出反馈鲁棒控制

王金湘　　代蒙蒙　　陈　南

(东南大学机械工程学院, 南京 211189)

考虑参数不确定性的汽车前轮主动转向输出反馈鲁棒控制

王金湘代蒙蒙陈南

(东南大学机械工程学院, 南京 211189)

摘要:提出基于静态输出反馈的前轮主动转向(AFS)鲁棒控制器,以提高汽车横摆角速度跟踪性能和横向稳定性．在控制器设计中考虑了车速和轮胎侧偏刚度的不确定性,其中车速在一定范围内变化并且可测,采用多胞型模型来描述车速的不确定性．利用多目标优化与输出反馈鲁棒控制方法,同时提高汽车横摆角速度跟踪性能和横向稳定性．在Matlab/Simulink和CarSim联合仿真环境中,对紧急转弯和双移线2种典型操纵工况下的控制器进行仿真试验．结果表明,所提出的控制器能够显著改善汽车的横向操纵性能和稳定性,降低驾驶员的工作负荷,且控制器对汽车模型参数的不确定性具有很好的鲁棒性．

关键词:车辆;前轮主动转向;输出反馈;鲁棒控制;参数不确定性

汽车横摆角速度跟踪性能和横向稳定性对汽车安全行驶非常重要,其控制方法是车辆工程领域研究的热点[1]．通过对车轮转向角或制动/驱动力矩的主动控制可以完成在临近极限工况下驾驶员难以实现的操纵．虽然制动/驱动力矩的主动控制在极限工况下产生附加横摆力矩的效果最佳,但同时也会对车辆纵向运动产生较大影响[1]．而前轮主动转向(AFS)控制几乎不影响纵向运动,并且在车辆轮胎力未达到附着极限的工况下能够产生较大的反方向横摆力矩,从而改善车辆的操纵稳定性[2]．

对于实际车辆系统,其模型参数是非线性时变的．车速随时间变化,而轮胎侧偏刚度随轮胎-路面附着系数和垂向轮胎载荷等参数的变化也具有不确定性．针对模型参数的时变和不确定性,Falcone等[3]采用模型预测控制方法实现汽车主动前轮转向路径跟踪控制．Do等[4]采用鲁棒滑模学习控制算法提高车辆线控转向的性能,控制算法不需要知道不确定的参数值．Nam等[5]采用一种基于乘积扰动模型的鲁棒控制方法实现主动转向控制,来提高车辆稳定性．Du等[6]基于线性参数可变(LPV)模型的状态反馈鲁棒控制实现横摆跟踪和车辆稳定性控制目标．文献[7-8]都同时考虑了可测时变参数和有界不确定参数,采用状态反馈的鲁棒控制进行横摆跟踪或轮胎驱动力分配控制．

基于测量输出的静态输出反馈鲁棒控制是控制理论和应用研究的热点[9]．该类控制器设计的难点是将双线性矩阵不等式转化为线性矩阵不等式(LMI),从而能够利用工具箱求解[10]．Benton等[11]给出了具有时变参数的不确定系统静态输出反馈控制器设计步骤,并将该控制器应用于车辆轨迹跟踪控制．Koroglu等[12]研究了考虑系统多性能目标的静态输出反馈控制的LMI条件．

状态反馈控制器实现时需要测量系统所有状态变量,但在汽车动力学控制实际应用中，准确测量或估计汽车侧向速度这一状态变量的成本较高[13-14]．另外,在考虑汽车横向运动的汽车模型中,车速和轮胎侧偏刚度均为模型参数,其中车速容易测量,但随时间变化具有不确定性,而轮胎侧偏刚度有界且不容易测量．本文考虑车速和轮胎侧偏刚度的不确定性,提出基于静态输出反馈的AFS鲁棒控制器,以提高汽车横摆角速度跟踪和侧向稳定性控制性能,降低控制器实现的难度．并在Matlab/Simulink和CarSim联合仿真环境中进行试验,验证所提出控制器的性能．

1汽车动力学模型和问题描述

本文采用如图1所示的二自由度汽车模型来设计控制器．

图1　二自由度汽车模型

假设前轮转向角不大,车辆模型可表示为

(1)

(2)

式中,m为汽车质量;Iz为车辆坐标系下汽车绕z轴的转动惯量;Vx和Vy分别为汽车纵向和横向速度;lf和lr分别为汽车前、后轴到质心的距离;r为汽车横摆角速度;Fyf和Fyr分别为前、后轴上的横向力,可表示为

Fyf=-2Cfαf,Fyr=-2Crαr

(3)

其中

(4)

式中,αf和αr分别为前、后轮胎侧偏角;δf为前轮转向角;β为汽车质心侧偏角,当质心侧向速度不大时可表示为β=Vy/Vx;Cf和Cr分别为前、后轮侧偏刚度,受轮胎-路面附着系数和轮胎垂向载荷等因素影响,具有不确定性．考虑该不确定性,轮胎侧偏刚度表示为[8]

(5)

把驾驶员输入的转向角δfd作为系统外部干扰,令w=δfd,并定义主动转向控制系统输入u=δfc,则前轮转向角可表示为δf=w+u．

控制器设计的目的是跟踪理想横摆角速度和质心侧偏角,其中理想质心侧偏角为0,而理想横摆角速度可表示为

(6)

式中,常数kus为汽车稳定性因数,可由线性二自由度汽车理想模型的参数决定[15]．

(7)

式中

A0(ρ)=

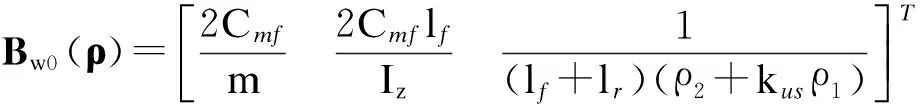
考虑静态输出反馈控制器设计,控制输入表示为

u=Ky

(8)

式中,K∈R1×2为控制增益;y为系统的测量输出,表示为

y=Cx+D(ρ)w

(9)

其中

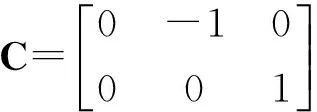
D(ρ)=[1/[(lf+lr)(ρ2+kusρ1)]　0]T

可见式(8)相当于PI控制．由式(7)～(9)可得输出反馈控制的闭环系统:

(10)

若分别将质心侧偏角和横摆角速度跟踪误差定义为系统控制输出,即令z1=0-β和z2=rd-r,可得

z1=C1(ρ)x+D1w

(11)

z2=C2x+D2(ρ)w

(12)

‖z1‖∞<γ‖w‖2,‖z2‖2<σ‖w‖2

(13)

式中，γ和σ为性能指标，分别用于表征汽车质心侧偏角和横摆角速度跟踪误差的大小.

综上所述,系统控制目标可描述为:设计合适的控制增益K,使得闭环系统(10)稳定,且使得式(13)定义的性能指标最小．

2输出反馈鲁棒控制器设计

本节设计考虑模型参数可变和不确定性的输出反馈控制器．假设输出反馈增益可表示为

K=NW-1

(14)

式中,N∈R1×2,W∈R2×2．首先,应用文献[12]推导的结论,可得以下引理．

引理1若存在对称正定阵Yi∈R3×3(i=1,2),矩阵N∈R1×2和W∈R2×2满足不等式

(15)

-φHe(W)φ(CY2-WC)+NTBTuφD(ρ)0*He[A(ρ)Y2+BuNC]Bw(ρ)YT2CT2**-σIDT2(ρ)***-σIéëêêêêêêùûúúúúúú

(16)<0

(17)

则闭环系统(10)稳定,且由式(14)得到的控制增益K满足式(13)．式中,ψ和φ为正实数,He(X)=X+XT．

为处理模型参数的不确定性,引入以下引理．

(18)

成立，当且仅当存在正实数ε,使得下式成立:

(19)

(20)

式中,Ωj为凸多面体的顶点,

(21)

点ρ相对于这些凸多面体顶点的坐标表示为

(22)

由引理1、引理2及式(20)～(22),可得如下定理．

定理1给定系统性能指标γ和σ,存在增益调度的输出反馈控制器使得闭环系统(10)渐进稳定且满足式(13),当且仅当存在正实数εlj和对称正定阵Yi∈R3×3(i=1, 2;l=1,2,…,8),矩阵Nj∈R1×2和矩阵Wj∈R2×2满足不等式

(23)

(24)

(25)

j=1,2,3,4

式(13)中有γ和σ两个性能指标,因此控制器设计是一个多目标优化问题,可以转化为给定其中一个性能指标σ,求另一性能指标γ最小化的问题．

推论1定理1中,给定σ,性能指标γ的最小值可以通过解以下最优化问题得到:

minγ

s.t.式(23)～(25)成立

j=1,2,3,4

(26)

由推论1,可求得凸多面体顶点上的控制增益Kj,进而计算得到某车速下的输出反馈控制器增益,即

(27)

式中,λj(ρ)根据式(22)计算．

3仿真试验和结果分析

建立Matlab/Simulink和CarSim联合仿真环境,对上述鲁棒控制算法进行仿真试验．首先在CarSim中建立非线性整车模型,Matlab/Simulink中建立上述鲁棒控制器模型,然后应用Matlab的LMI工具箱来求解式(26)中的最优化问题．仿真中轮胎-路面附着系数为0.85．整车模型主要参数如表1所示．

表1　整车模型主要参数

在仿真中,假定参数Vx的变化范围是[18, 28] m/s．考虑轮胎的非线性特性,假定侧偏刚度的变化范围为±30%,即Cminf=72 191 N/rad,Cmaxf=134 069 N/rad,Cminr=51 697.8 N/rad,Cmaxr=96 010.2 N/rad．给定σ值为15,通过推论1对(ψ,φ)进行二维搜索,得到当ψ=5.2,φ=3.9时,γ最小值为6.3．此时,求得式(21)所描述凸多面体上4个顶点的控制增益分别为

(28)

由这些控制增益值和式(27)可计算输出反馈控制器增益．

在紧急转弯(J-turn)和双移线2种极限操纵工况下对上述控制算法进行了仿真试验．

3.1紧急转弯工况仿真

紧急转弯操纵工况的车速为20 m/s,驾驶员转向角输入δfd由0很快增大到3°,模拟汽车紧急转弯的极限工况,如图2所示．

图2　紧急转弯操纵工况下转向角

仿真结果如图2和图3所示．由图3可知,由于转向角较大且车速较高,无控制的汽车不能跟踪理想横摆角速度,侧向加速度和质心侧偏角最大值分别达到8.1 m/s2和6.9°,发生了非常明显的侧滑．当采用上述AFS鲁棒控制时,虽然实际横摆角速度与理想横摆角速度相比产生了14%左右的超调,侧向加速度最大值也达到了7.7 m/s2,但系统很快趋于稳定,且横摆角速度跟踪稳态误差趋于零,汽车质心侧偏角最大值仅为1.4°,未发生侧滑．可见采用上述鲁棒控制后,能够显著提高紧急转弯极端操纵工况下汽车的横摆角速度跟踪效果和稳定性．

(a) 横摆角速度

(b) 侧向加速度

(c) 质心侧偏角

3.2双移线工况仿真

该操纵工况的车速为24 m/s,路径采用ISO国际标准的双移线试验路径．用来跟踪该路径的驾驶员模型描述为[16]

(29)

式中,τL和τd2分别为超前和滞后时间常数;τd1为描述驾驶员反应的纯延时;Gh为转向比例增益;GR为车辆转向系的转向比; ΔY(s)为当前车辆质心的横向位置和预瞄点横向位置之间的偏差．仿真采用的驾驶员模型参数为τL=0.09 s,τd1=0.06 s,τd2=0.20 s,Gh=0.7,预瞄时间为0.8 s．采用上述输出反馈控制来跟踪驾驶员操纵意图的仿真试验框架如图4所示．

图4　双移线工况仿真控制框图

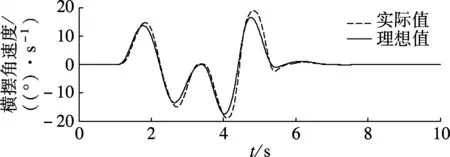
仿真试验结果如图5～图8所示．由于驾驶员模型参数表征的是非熟练驾驶员,驾驶员反应所需时间较长．在未加控制时驾驶员虽然完成了双移线操纵,但汽车横摆角速度跟踪误差较大,汽车侧向加速度和质心侧偏角分别达到了7.8m/s2和3.9°．移线后车辆仍未稳定,驾驶员还需要调整转向角才能使车辆回到稳定状态,驾驶员的工作负荷较大． 另一方面, 由图5(a)可知AFS鲁棒控制器对前轮转向角进行了小角度调整．有控制时横摆角速度跟踪误差较小,且侧向加速度和质心侧偏角最大值明显减小,分别只有6.3m/s2和1.4°,驾驶员能够更轻松实现移线,而且完成移线后车辆迅速回到稳定状态,驾驶员不需过多地调整转向角．综上所述,上述AFS鲁棒控制器能够改善双移线工况下车辆操纵和稳定性能,并且能降低驾驶员操纵的工作负荷．

(a) 有控制

(b) 无控制

(a) 有控制

(b) 无控制

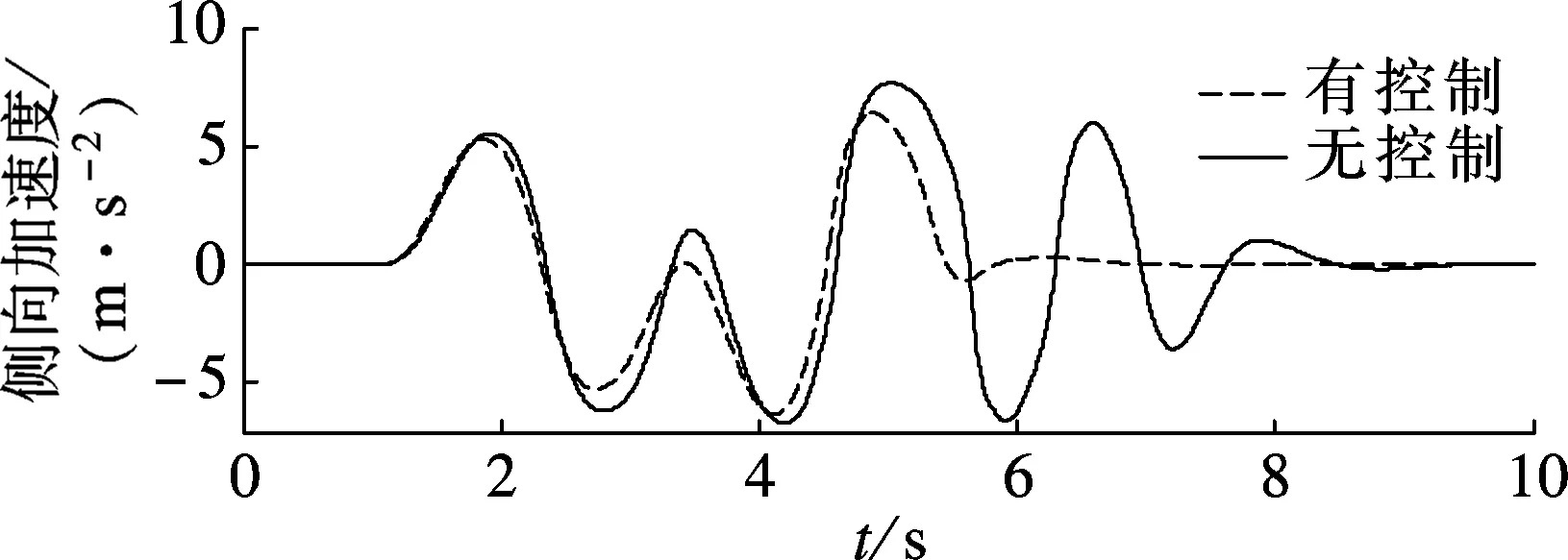
(a) 侧向加速度

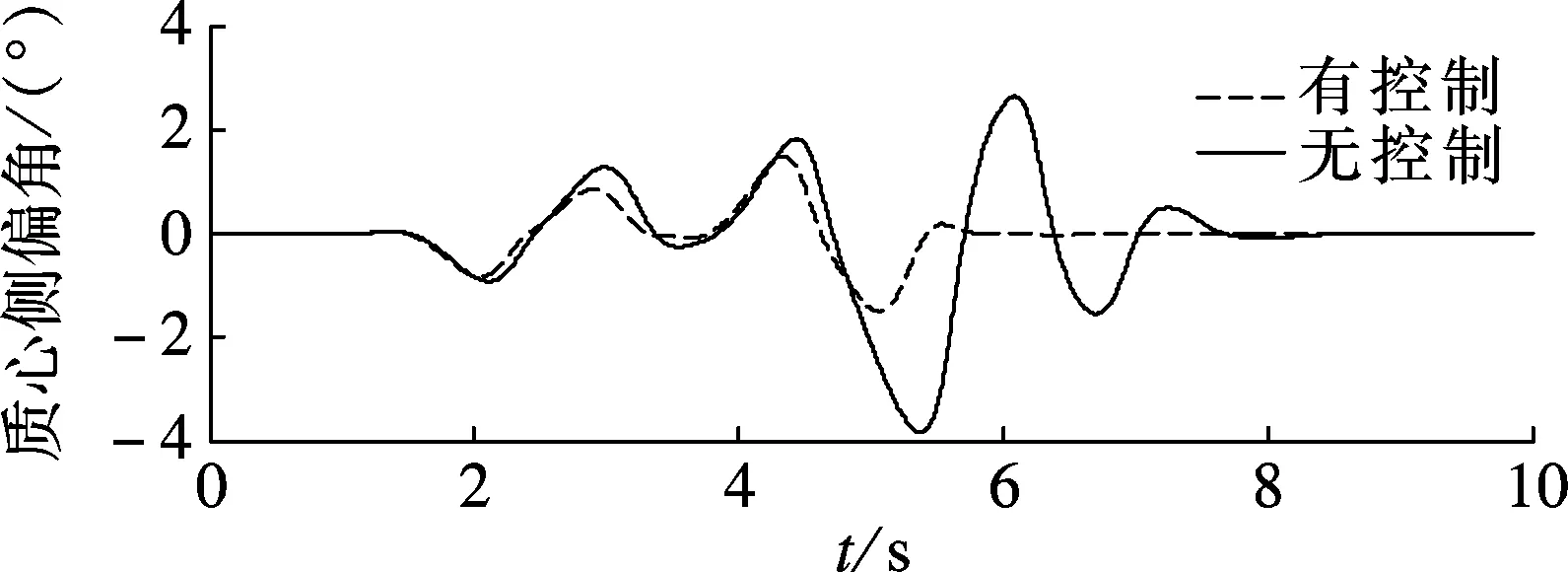
(b) 质心侧偏角

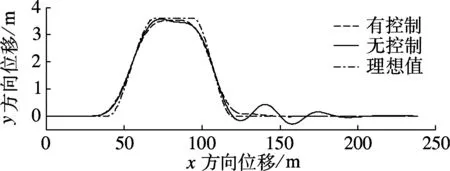
图8　双移线操纵工况下汽车质心位移

4结语

本文考虑车速和轮胎侧偏刚度的不确定性,提出了基于静态输出反馈的AFS鲁棒控制器以提高汽车横向操纵性能和稳定性．并在Matlab/Simulink和CarSim联合仿真环境中进行紧急转弯和双移线等极限操纵工况仿真试验,验证所提出控制器的性能．仿真试验结果表明,所提出的AFS鲁棒控制器能够显著改善车辆的横向操纵性能和稳定性．在仿真工况下侧偏刚度接近轮胎附着极限的非线性范围,同时车速也具有时变性,结果表明控制器具有很好的鲁棒性．另一方面,控制器只需测量横摆角速度和车速等系统输出量,不必进行汽车侧向速度的测量或估计,降低了控制器实现的成本．

参考文献(References)

[1]ManningWJ,CrollaDA.Areviewofyawrateandsideslipcontrollersforpassengervehicles[J]. Transactions of the Institute of Measurement and Control, 2007, 29(2):117-135.DOI:10.1177/0142331207072989.

[2]HeJ,CrollaD,LevesleyM,etal.Integratedactivesteeringandvariabletorquedistributioncontrolforimprovingvehiclehandlingandstability[J]. SAE Transactions, 2004, 113(6):638-647.

[3]FalconeP,BorrelliF,AsgariJ,etal.Predictiveactivesteeringcontrolforautonomousvehiclesystems[J].IEEE Transactions on Control Systems Technology, 2007, 15(3):566-580.DOI:10.1109/tcst.2007.894653.

[4]DoMT,ManZH,ZhangCS,etal.Robustslidingmode-basedlearningcontrolforsteer-by-wiresystemsinmodernvehicles[J]. IEEE Transactions on Vehicular Technology, 2014, 63(2): 580-590.DOI:10.1109/tvt.2013.2280459.

[5]NamK,OhS,FujimotoH,etal.Robustyawstabilitycontrolforelectricvehiclesbasedonactivefrontsteeringcontrolthroughasteer-by-wiresystem[J]. International Journal of Automotive Technology, 2012, 13(7):1169-1176.DOI:10.1007/s12239-012-0120-6.

[6]DuHP,ZhangN.Robustyawmomentcontrolforvehiclehandlingandstabilityimprovement[C]//24th Chinese Control and Decision Conference.Taiyuan,China, 2012: 4221-4226.

[7]ZhangH,ZhangXJ,WangJM.Robustgain-schedulingenergy-to-peakcontrolofvehiclelateraldynamicsstabilisation[J]. Vehicle System Dynamics, 2014, 52(3):309-340.DOI:10.1080/00423114.2013.879190.

[8]WangR,ZhangH,WangJ.Linearparameter-varyingcontrollerdesignforfour-wheelindependentlyactuatedelectricgroundvehicleswithactivesteeringsystems[J]. IEEE Transactions on Control Systems Technology, 2014, 22(4): 1281-1296.

[9]DongJ,YangGH.Staticoutputfeedbackcontrolsynthesisforlinearsystemswithtime-invariantparametricuncertainties[J]. IEEE Transactions on Automatic Control, 2007, 52(10): 1930-1936.

[10]ZhangH,ShiY,MehrAS.RobuststaticoutputfeedbackcontrolandremotePIDdesignfornetworkedmotorsystems[J]. IEEE Transactions on Industrial Electronics, 2011, 58(12): 5396-5405.DOI:10.1109/tie.2011.2107720.

[11]BentonRE,SmithD.Astatic-output-feedbackdesignprocedureforrobustemergencylateralcontrolofahighwayvehicle[J]. IEEE Transactions on Control Systems Technology, 2005, 13(4):618-623.DOI:10.1109/tcst.2004.841681.

[12]KorogluH,FalconeP.NewLMIconditionsforstaticoutputfeedbacksynthesiswithmultipleperformanceobjectives[C]//IEEE 53rd Annual Conference on Decision and Control.LosAngeles,CA,USA, 2014: 866-871.DOI:10.1109/cdc.2014.7039490.

[13]NamK,OhS,FujimotoH,etal.EstimationofsideslipandrollanglesofelectricvehiclesusinglateraltireforcesensorsthroughRLSandKalmanfilterapproaches[J]. IEEE Transactions on Industrial Electronics, 2013, 60(3): 988-1000.DOI:10.1109/tie.2012.2188874.

[14]YoonJH,PengH.RobustvehiclesideslipangleestimationthroughadisturbancerejectionfilterthatintegratesamagnetometerwithGPS[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1):191-204.DOI:10.1109/tits.2013.2275173.

[15]余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009: 144-162.

[16]PlöchlM,EdelmannJ.Drivermodelsinautomobiledynamicsapplication[J]. Vehicle System Dynamics, 2007, 45(7):699-741.DOI:10.1080/00423110701 432482.

Robust output feedback control for vehicle active front wheel steering system considering parameter uncertainties

Wang JinxiangDai MengmengChen Nan

(School of Mechanical Engineering, Southeast University, Nanjing 211189,China)

Abstract:A robust static output feedback controller for active front wheel steering (AFS) is proposed to improve the performance of vehicle yaw rate tracking and lateral stability. The modeling uncertainties including vehicle velocity and cornering stiffness are considered in the controller design. The vehicle velocity is variable and measurable, and the polytope model is applied to deal with the uncertainty of vehicle velocity. With the combination of the multi-objective optimization and the output feedback robust control, the performance of the tracking vehicle yaw rate and lateral stability is improved. In the co-simulation environment including Matlab/Simulink and CarSim, simulations under the typical handling conditions of J-turn and double lane change are conducted to verify the performance of the proposed controller. Simulation results show that the performance of vehicle handling and stability is improved with the proposed controller, and the workload of the driver is reduced. The results also show that the proposed controller is robust to the parameter uncertainty of the vehicle model.

Key words:vehicle; active front wheel steering; output feedback; robust control; parameter uncertainty

doi:10.3969/j.issn.1001-0505.2016.03.004

收稿日期:2015-11-11.

作者简介:王金湘(1979—),男,博士,讲师,wangjx@seu.edu.cn.

基金项目:国家自然科学基金资助项目(51205058,51375086).

中图分类号:U461; TP273

文献标志码:A

文章编号:1001-0505(2016)03-0476-07

引用本文:王金湘,代蒙蒙,陈南.考虑参数不确定性的汽车前轮主动转向输出反馈鲁棒控制[J].东南大学学报(自然科学版),2016,46(3):476-482. DOI:10.3969/j.issn.1001-0505.2016.03.004.