基于概率感知模型的有向传感器确定性部署研究

雷雨潼 张军国

（北京林业大学 工学院，北京 100083）



基于概率感知模型的有向传感器确定性部署研究

雷雨潼 张军国

（北京林业大学 工学院，北京 100083）

摘 要：节点部署是无线传感器网络技术应用过程中的关键问题。为了更加精确地描述网络对物理世界的感知范围和质量，本文采用由自身物理特性等诸多因素决定的概率感知节点对监测区域进行无缝覆盖。针对无线有向传感器网络中节点的概率感知特性，通过数值仿真，从冗余覆盖面积及感知概率两方面，分析比较采用不同确定性部署方式对同一监测的无缝覆盖。实验结果对区域覆盖的确定性节点部署方式的选择具有重要的指导性意义。

关键词：有向传感器网络 概率感知模型 确定性 节点 冗余覆盖面积

引言

近年来，随着无线多媒体技术的迅速发展，对图像、视频、音频等数据的监测需求越来越多，有向传感器网络应运而生。作为无线传感器网络进行工作的第一步，节点部署关系着网络监测信息的时效性、准确性和完整性［1］。

作为目前无线传感器网络领域的研究热点，有向节点的部署引起国内外很多学者的广泛关注。文献［2］扩展传统有向传感器的覆盖问题，提出了一种基于贪婪策略的近似算法。文献［3］针对无线传感器网络中的有向感知模型，提出了一种基于复杂网络社会结构划分的覆盖增强算法。该算法在节点随机选取感知方向部署完成后，通过模块性来衡量网络质量，并重新调整节点的感知方向，以增强网络的覆盖性能。文献［4］推导了各节点调节感知方向的改变量，形成一个节点方向调度规则和分布式算法。

上述算法均采用理想化的布尔模型［5］，目前对于概率感知模型［6-7］的部署研究大多集中在随机部署方式上，关于有向感知节点的确定性部署研究较少。文献［8］针对随机部署提出一种基于感知概率模型的节点部署方案。文献［9］提出了一种新的动态视觉传感器目标物体覆盖率问题。文献［10］则针对有向感知节点的布尔模型，提出了一个面向目标覆盖的最优确定性部署方法。

在对于网络状态稳定环境信息良好的实际应用中，为获得完整的监测信息，对区域覆盖的概率模型确定性部署有了迫切需求。在区域覆盖中，节点部署的目标是用最少的传感器节点实现最大面积的有效覆盖，并达到一定的监测概率。因此，本文在满足节点间通信的前提下，对有向感知节点的概率感知模型的部署进行研究。文章通过对同一监测区域内采用不同确定性部署的冗余覆盖和监测概率进行分析对比，从而为区域监测的确定性部署方式提供选择标准。

1 问题描述

1.1 感知模型

有向感知节点的概率感知模型通常被定义在二维空间内。节点感知范围是一个以节点为圆心、以感知距离为半径的扇形区域，如图1所示。P表示节点的位置坐标；rs表示传感半径；re为节点感知概率为1的最大半径；为节点视角偏移量，即1/2感知夹角。

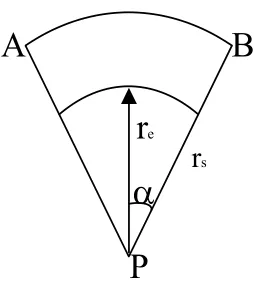
图1 不可转动扇形感知模型

传感器节点对监测区域内任意位置点q在概率感知模型下的数学表达式［11］为：

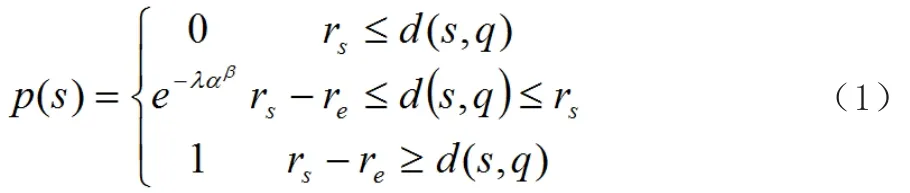
1.2 覆盖模型

为获取有效感知数据信息，将监测区域用正方形网格进行划分，分别采用平铺部署方式和将扇形感知节点组合成圆的圆形部署方式来对监测区域进行覆盖，如图2所示。

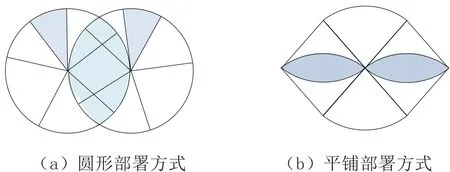
图2 实现区域实时完全覆盖的部署方式

对于组合而成的圆形，通过规格化覆盖算法确定圆心位置。通常采用的规格图形有三大类：三角形、四边形和六边形。对于四边形和六边形，又可根据改变内角的方式分为正方形、菱形、正六边形和非正等边六边形。

2 确定性部署中的冗余覆盖

鉴于有向传感器节点感知模型的图像特征，在进行区域覆盖的完全部署时会产生重叠监测区域。尽可能增大有效覆盖面积，减少重叠覆盖，是进行区域覆盖目标之一。

2.1 冗余覆盖面积

对于平铺部署方式而言，重叠覆盖的面积与传感器节点的感知夹角相关。感知夹角的不同，决定了两个相对的节点的部署距离。在这种部署方式下，平均到每个节点的重叠面积为

对于圆形方式，产生的冗余覆盖如图2（a）阴影部分所示。它主要由两部分组成：一部分是由组成圆的扇形传感器节点的感知夹角产生；一部分是由采用的规格图形产生。对于内角规定的等边三角形、正方形和正六边形，圆形部署方式下的冗余覆盖面积为：

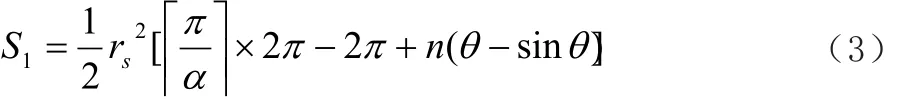
其中，n表示在形成一个规格图形的重叠个数；θ为重叠面积所对应的圆心角。

对于菱形和非正等边六边形，需要考虑内角的取值。在菱形部署方式下，两个角度不同的内角所对应的重叠面积大小不同，因此计算菱形的重叠覆盖时，需要分别对这两个内角对应的区域进行研究，如图3所示，计算公式为：

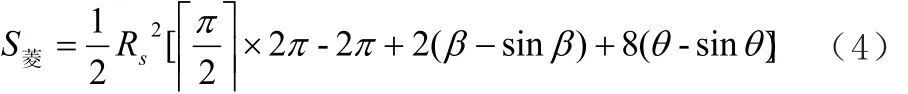
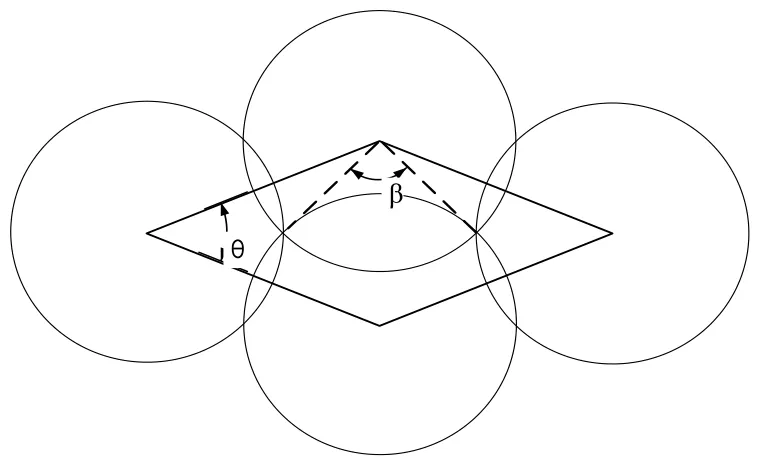
图3 菱形部署方式冗余覆盖

在使用非正等边六边形进行部署时，为使重叠面积最小，首先确定O2、O5的位置，即将O2、O5的圆心部署在非正等边六边形a、b点上，O1、O6与O2、O5相交于点c，圆心在同一直线上。同理，确定O3、O4的位置，与O2、O5相交于点d。

由O2的圆心向圆交点c、d分别引出两条直线，长度为rs。

O2到O5的距离为：

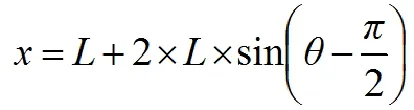
重叠面积所对应的圆心角分别为：

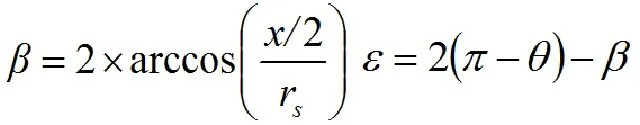
则一个非正等边六边形的圆间重叠面积为：

图4 非正等边六边形部署方式下的冗余覆盖

2.2 冗余覆盖概率

采用物理特性相同的同构节点进行部署，因此具有相同的不确定度量值及衰减系数，且每个节点在监测区域内对目标的感知概率相互独立，则两个节点在监测区域内重叠的联合概率密度为：

用x1和x2分别表示节点A、B在监测区域内的位置，d表示两节点重叠距离。要使两节点不重叠，则必须满足：

则计算节点的重叠概率Py（Sy）应将两节点重叠的联合概率密度p（x，y）在上式的范围内积分：

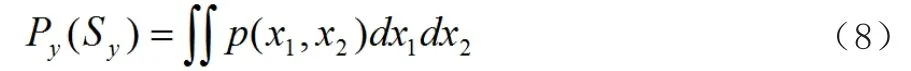
于是，有：

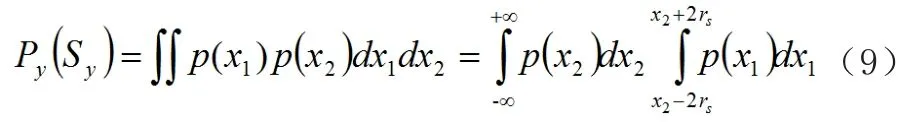
对于监测区域内的确定性部署方式，每一个节点的位置固定不变。因此，在实际应用中重叠区域的监测概率Py（Sy）计算公式为：

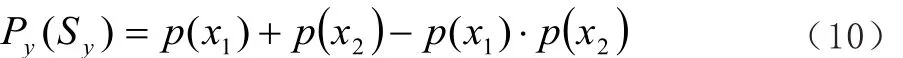
3 实验仿真

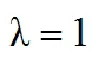
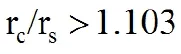
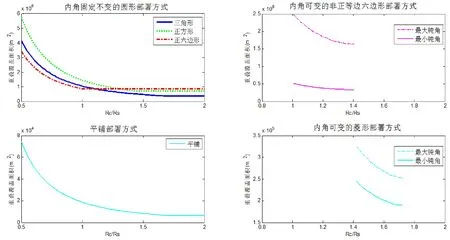
图5 不同部署方式下重叠面积与通信半径之间的关系

对于采用概率模型进行监测的目标区域来说，感知概率越高，节点对目标信息获取越多，覆盖的服务质量越好。对于产生冗余覆盖的确定性部署方式，为实现无缝覆盖，降低了有效覆盖率。但是，由于节点对目标的感知相互独立，产生的冗余覆盖提高了目标区域内的感知概率。对目标点与节点的距离和感知概率的关系进行仿真，结果如图6所示。在采用正六边形进行部署时，监测区域内可以实现0-1覆盖，即整个监测区域被传感器节点感知到的概率衡为1。对于冗余覆盖面积最小的平铺部署方式来说，当目标点在传感器节点感知概率为1的最大半径外时，节点对目标的感知概率衰减速度较快，且感知能力较差。

图6 感知概率与目标和节点之间距离的关系

3 总结

本文通过对概率感知模型的有向传感器节点在监测目标内进行区域覆盖的确定性部署，研究在保证监测区域的无缝覆盖以及通信要求下，需要的传感器节点个数、产生冗余覆盖与通信半径之间的关系，以及节点对目标的感知能力。通过对选取的6种方式进行仿真实验，发现在通信半径与感知半径的比值小于1.103，且采用正六边形部署方式时，既能保证使用节点数最少，同时可以获得最高的感知概率。对于感知能力要求较高，所需获得的数据信息严格的区域，首先考虑正六边形部署方式。当通信半径与感知半径之比大于1.205时，对于对感知概率没有明确要求的一般物理环境来说，考虑经济等其他因素，可选用平铺部署方式进行覆盖监测。

参考文献

［1］J. G. Zhang，W. Li，X. Zhao，X. Bai，C. Chen. Simulation and Research on Data Fusion Algorithm of the Wireless Sensor Network Based on NS2［C］. Proceedings of 2009 WRI World Congress on Computer Science and Information Engineering，Los Angeles，2009：66-70.

［2］李靖，王汝传，黄海平，等.有向传感器网络覆盖控制策略［J］.通信学报，2011，（8）：118-127.

［3］周有为，张君，晁志超.一种基于有向感知模型的传感器节点覆盖算法［J］.电子设计工程，2013，（24）：23-25.

［4］G. Fusco，G. Himanshu.Selection and Orientation of Directional Sensors for Coverage Maximization［J］.IEEE Communications Society Conference on Sensor，Mesh and Ad Hoc Communications and Networks，2009，（1）：1-9.

［5］H. D. Ma，Y. H. Liu.On Coverage Problems of Directional Sensor Networks［J］.Springer

Berlin Heidelberg，2005，（3794）：721-731.

［6］J. Lu，T. Suda.Coverage-aware Self-scheduling in Sensor Networks［J］.IEEE Annual Workshop on Computer Communications，2003，（1）：117-123.

［7］L. P. Jiang，L. M. Wang，S. M. Xiong，et al.K-coverage Algorithm Based on Probabilistic Sensing model in WSN［J］. Application Research of Computers，2009，（9）：3483-3484.

［8］腾贺，吴成东，张云洲，等.有向无线传感器节点概率感知模型的设计［J］.江南大学学报：自然科学版，2012，（4）：391-395.

［9］彭力，王茂海，赵龙.一种新的动态视觉传感器网络目标覆盖率算法［J］.计算机应用研究，2010，（5）：1708-1710.

［10］李强懿，马冬前，张聚伟.基于感知概率的无线传感器网络节点部署算法［J］.计算机测量与控制，2014，（2）：643-645.

［11］蒋丽萍，王良民，熊书明，等.基于感知概率的无线传感器网络k重覆盖算法［J］.计算机应用研究，2009，（9）：3484-3486，3489.

Deterministic Deployment of Sensors Based on Probabilistic Sensing Model

TONG Yutong，ZHANG Junguo
（School of engineering， Beijing Forestry University， Beijing 100083）

Abstract:Node deployment is a key problem in the application of wireless sensor network technology. In order to describe the scope and quality of the physical world more accurately， this paper uses the probability sensing nodes， which are determined by the physical characteristics and other factors， to make seamless coverage of the monitoring area. Aiming at the wireless to the probability sensing properties of the nodes in the sensor network， through the numerical simulation， from redundant coverage area and the perceived probability of two aspects. Analysis was used to compare different deterministic deployment of monitoring the same seamless coverage. The results show that when the non positive equilateral hexagon， obtained relatively good perceived probability and at the same time， produce the redundancy in covering area of the smallest. Obviously， the experimental results have important guiding significance for the selection of the regional coverage of the deterministic node deployment method.

Key words:directed sensor networks， probabilistic sensing model， deterministic， node， redundant coverage area

基金项目：国家自然基金（31300470）；中央高校基本科研业务费专项资金（2016ZCQ08）。