利用太阳光压的大偏心率伴飞卫星轨道控制∗

侯永刚赵长印张明江孙荣煜

(1中国科学院紫金山天文台南京210008)(2中国科学院空间目标与碎片观测重点实验室南京210008)(3中国科学院大学北京100049)

利用太阳光压的大偏心率伴飞卫星轨道控制∗

侯永刚1,2,3†赵长印1,2张明江1,2孙荣煜1,2

(1中国科学院紫金山天文台南京210008)
(2中国科学院空间目标与碎片观测重点实验室南京210008)
(3中国科学院大学北京100049)

提出了利用太阳帆进行大偏心率伴飞卫星轨道控制的方法.伴飞卫星围绕其惯量主轴做角速度恒定的自转,其惯量主轴在惯性系内指向保持不变.对伴飞卫星的控制分为轨道面的控制和轨道面内控制两部分.在控制过程中,优先考虑轨道面内的控制,在轨道面内控制不能进行(或者因为几何原因不能进行轨道面内控制)时,进行轨道面的控制.通过滑膜控制方法(Sliding Mode Control)计算轨道面内控制需要的控制力的方向和大小.得到需求的控制力要求后,推算出在控制过程中太阳帆相对于伴飞卫星主体的角度解析表达式.通过控制太阳帆的方向得到所需的不同的控制力.整个控制过程只针对伴飞卫星,主星处于自然飞行状态.最后对于这种控制方法进行数值验证.在无摄运动状态下通过控制系统进行伴飞轨道的轨道调整和误差消除,在考虑4阶非球形引力和第三体引力摄动情况下进行伴飞轨道的轨道维持.数值结果表明通过这种控制方法伴飞轨道能够保持轨道误差小于5 m.

航天器,天体力学,方法:数值

1 引言

伴飞轨道的设计、控制和应用是目前空间科学的热门研究领域之一,经过二十多年的发展,取得了丰富的成果.通过伴飞卫星和主卫星协作或者几个卫星组成编队等协作方式,空间卫星能够完成很多复杂的空间任务.相比于传统的单个大卫星,编队卫星有费用低、可替换性高、灵活性大、应用范围广等优点,在实际应用中有广阔的市场.在各种摄动力的影响下,伴飞轨道并不能够保持稳定,伴飞卫星和主星之间的几何关系需要通过不断地调整轨道来保持.这个控制过程需要消耗很多星载燃料.因此减少控制过程中的燃料消耗成为现在伴飞轨道研究中最主要的问题.

减少控制过程的燃料消耗主要有两个途径.一是通过初始轨道设计,减少已知的轨道摄动因素(主要是地球非球形引力摄动J2项和其他有明确的长期项作用的摄动因素)对伴飞轨道的影响,从而减少对伴飞轨道的控制次数和控制力.二是通过优化控制策略使得燃料的利用率增加来达到节省燃料的目的.许多系统控制方法被应用在伴飞轨道控制的领域,比较典型的有线性系统的控制方法、LQR控制和非线性系统控制方法滑膜控制等[1−3].通过调整控制方案,可以在一定范围内节省燃料.由于控制力通过化学燃料来提供,星载燃料的消耗仍旧是不可避免的.本文提出的应用太阳光压作为控制力能够更大限度节省燃料.

大偏心率轨道在近地点和远地点处的轨道高度差距非常大,在一个周期中卫星经历包括低轨和中高轨等各种不同的空间环境.因此大偏心率卫星在空间探测以及通信导航等领域有着很广泛的应用.大偏心率轨道上同样可以设计伴飞轨道,比如已经发射成功的Cluster II编队卫星,整个系统由4个卫星组成四面体结构,在近地点能够进行地球重力场的观测,在远地点能够进行太阳风和空间天气的观测[4].

利用小推力进行轨道的控制和演化已经被很多学者提出并进行比较深入的研究[5−8].在卫星上安装太阳帆和大气阻尼帆板,通过太阳光压的作用力和大气的作用力进行轨道控制同样也可以视为应用小推力进行轨道控制.通过适当调整太阳帆的角度能够消除升交点经度的长期演化对伴飞轨道的破坏[9],验证了在轨道面内通过这两种自然作用力进行轨道控制的可行性[10].但是这些研究都是主要针对主星轨道为近圆轨道的伴飞类型,并且设定卫星为三轴稳定型卫星.主星轨道为大椭圆时,伴飞卫星相对于主星的轨道发生很大变化,轨道形状不再是椭圆.动力学系统不能够用线性系统表示.在控制策略的制定时,不能应用已经很成熟的线性控制策略,需要设计新的控制机制.

本文将研究主从卫星的伴飞方式,主星的轨道为大偏心率轨道,主星不依靠太阳光压进行控制(实际状况中主星质量比较大,应用太阳光压控制不合理),伴飞卫星上安装有太阳帆以提供控制力.伴飞卫星在地球质心惯性坐标系(Earth Centrical Inertial coordinate,ECI)下保持稳定自旋,并且自旋角速度方向与其惯量主轴重合,在飞行过程中,惯量主轴在ECI中方向保持不变.控制通过反作用轮对太阳帆与伴飞卫星主体的相对角度进行调整来实现.控制过程中优先考虑轨道面内的控制.当轨道面内的控制完成或者因为几何角度不满足轨道面内控制条件时,进行轨道面控制.在伴飞卫星的初始轨道设计和轨道重构的轨道设计中,考虑非球形引力摄动J2项长期项的影响.

本文第2部分介绍伴飞运动的非线性动力学模型,包括几种不同的坐标系和控制系统中的相对运动的非线性运动方程.第3部分为具体的控制策略表述,包括在飞行过程中太阳帆相对伴飞卫星主体的角度的控制和利用滑膜方法得到轨道面内控制时对控制力的要求.第4部分通过数值验证证明本文提出的方法切实可行,包括伴飞卫星的轨道重构和入轨误差的消除.第5部分总结本文提出的方法并对未来的应用状况做出展望.

要准确描述伴飞轨道的相对运动需要应用不同的坐标系,本文采用3个坐标系系统.对伴飞轨道进行控制和重构需要精确的动力学模型,包括无摄条件下伴飞轨道的动力学描述和摄动力(包括控制力和对伴飞轨道造成破坏的摄动力)作用下的摄动运动方程.

2 基础知识

2.1 坐标系系统

J2000地球质心惯性系(ECI):原点为地球的质心,参考平面为J2000历元的平赤道, X轴指向为J2000历元的平春分点,记做O−XY Z.

主星轨道坐标系(Local Vertical Local Horizontal frame,LVLH):原点为主星的质心,参考平面为主星的轨道面,x轴指向为主星的矢径的方向,y轴的指向为与主星运动方向同侧垂直于x的方向,z轴指向为主星的角动量方向,记做o−xyz.

伴飞卫星本体坐标系:原点为伴飞卫星的质心,z′轴指向为伴飞卫星自转角动量的方向,x′指向为太阳光和z′轴组成的平面与参考平面的交线中与x同向的方向,记做o′−x′y′z′.

2.2 相对运动方程

在主星LVLH坐标系中,伴飞卫星的位置矢量为[11]:

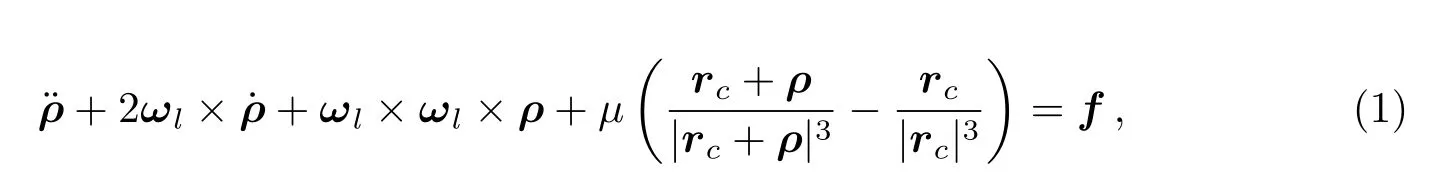
其中ρ=[x,y,z]T表示伴飞卫星在主星LVLH坐标系下的位置.ωl代表主星轨道的瞬时角速度,µ代表地球引力常数,rc代表主星在ECI坐标系中的位置,f代表除去地球中心引力外的其他所有力的作用,包括摄动力和控制力.伴飞卫星相对主星的位置矢量大小远小于主星相对于地心的位置矢量大小,因此有|ρ/rc|≪1,将其代入(1)式中,并且保留其1阶量,可以得到相对运动方程的简化形式[11]:

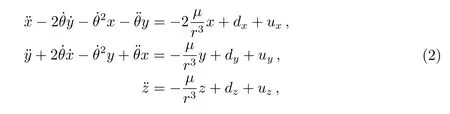
其中θ=ω+f为纬度幅角,ω是主星轨道的近心点角距,f是真近点角.d=[dx,dy,dz]T是相对摄动力,u=[ux,uy,uz]T是控制力.通过椭圆轨道的关系式:

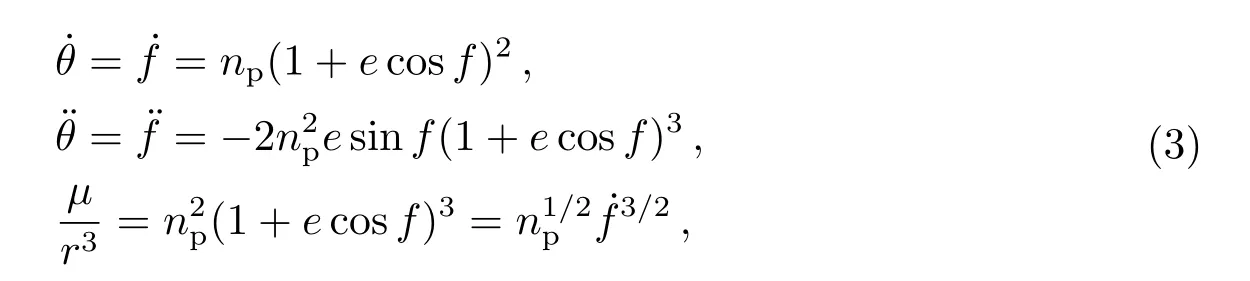
其中np是主星轨道的平运动角速度,e为主星轨道的偏心率,可以把(3)式简化为下列矩阵形式[11]:

其中A和B均为3×3阶矩阵,其具体的表达形式为[10]:

对于大偏心率轨道,动力学系统为非线性系统.在控制过程中,动力学系统会由于不同的初始状态量的变化而变化,因此要设计特殊的控制系统进行控制.

主星的开普勒轨道根数为σ=[a,e,i,ω,Ω,M]T,伴飞卫星的相对轨道根数记做δσ=[δa,δe,δi,δω,δΩ,δM]T.通过矩阵旋转能够用轨道根数得到ρ的表达方式为:

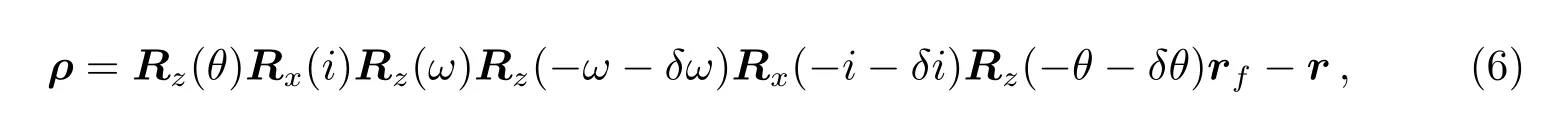
其中Rx、Rz分别表示绕x、z轴的旋转矩阵,rf、r分别表示伴飞卫星和主星的位置矢量.相对轨道根数δσ均为小量,经过线性化之后可以得到用相对轨道根数1阶量表示的伴飞卫星的相对位置为[12]:

3 控制系统

控制系统包括硬件系统和软件系统两个部分.太阳帆的安装以及其相对姿态调整是整个控制系统的基础.对于不同的飞行状态,采用不同的控制策略,通过对太阳帆的调整,保持系统的稳定.

3.1 携带太阳帆的伴飞卫星构造以及角度调整

安装太阳帆的伴飞卫星的构造如图1所示,伴飞卫星的主体为圆柱形,太阳帆为长方形并且通过连接杆与伴飞卫星的主体相连.ns为轨道平面法线单位矢量,α表示轨道平面法线方向与伴飞卫星自转轴夹角的余角.太阳帆与连接杆固连,连接杆与伴飞卫星主体之间通过两个反作用轮相连.连接杆为圆柱形,通过反作用轮的控制,连接杆能够围绕其旋转轴做角度为0◦↔360◦的旋转,同时连接杆本身能够绕伴飞卫星的主体旋转,旋转角度为−90◦↔90◦.在调整太阳帆的过程中,反作用轮消耗一定的能量,这些能量可以通过与太阳帆相连的太阳能电池提供,并不需要消耗伴飞卫星上的燃料.两个太阳帆完全相同,对称分布在伴飞卫星主体的两侧.在控制过程中,这种对称的构造能够使伴飞卫星保持旋转稳定性,不会增加额外的角速度.

图1 携带太阳帆的伴飞卫星构造Fig.1 The construction of the follower with solar wings

如图2所示,在坐标系o1−x1y1z1中,p平面垂直于坐标系的参考平面o1−x1y1,伴飞卫星的太阳帆连接杆的自选旋转轴在p平面内,γ为平面o1−x1z1与平面p的夹角,是表征卫星自旋的角度量.b表示伴飞卫星的太阳帆连接杆的自选旋转轴的指向,ϕ表示太阳帆连接杆与伴飞卫星自转轴之间的夹角,其表征连接杆相对于伴飞卫星主体之间的相对方向调整.n表示太阳帆的法线方向的单位矢量,β为太阳帆法线方向与平面p之间的夹角,其表征连接杆的自旋.F表示需要的摄动力的方向,ζ表示摄动力与x1的夹角.

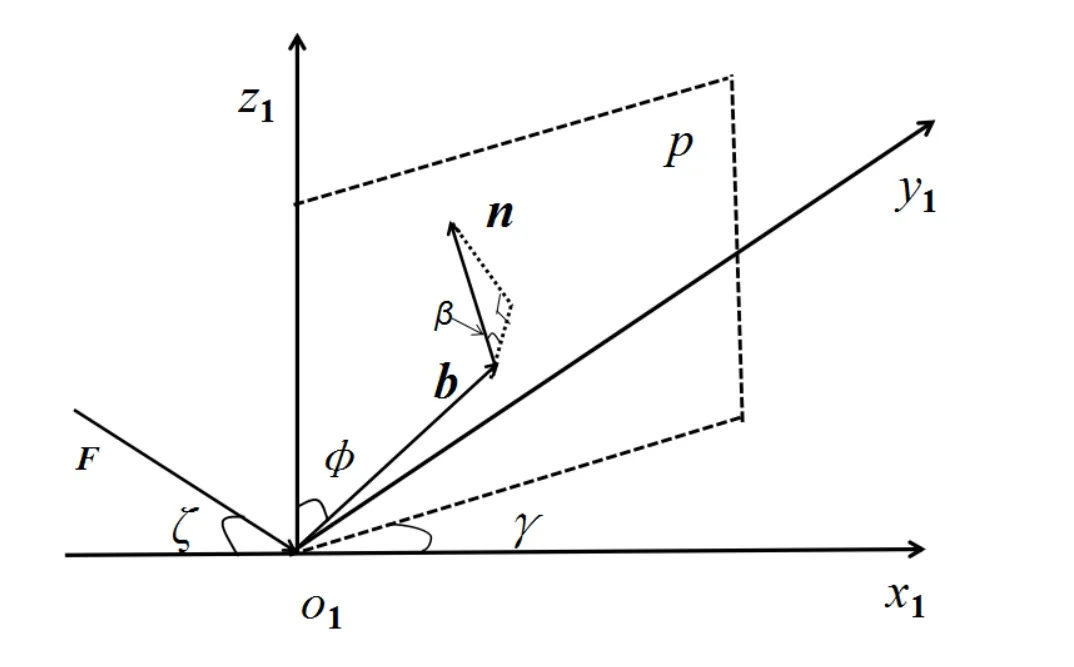
图2 伴飞卫星本体坐标系Fig.2 The body- fixed frame of the follower

控制力来源于太阳光压,其中太阳光压产生的摄动加速度为[9]:

其中p0=4.624×10−6N·m−2为光压常数,1＜q＜2为光压系数,s为两个太阳帆的总面积,m为伴飞卫星的总质量,L表示太阳光照射的方向,假定太阳光为平行光.控制力的方向均通过调整太阳帆来达到.在o1−x1y1z1坐标系中,太阳帆法向向量n可以用图2中定义的几个角度量来表示,其具体表达式为:

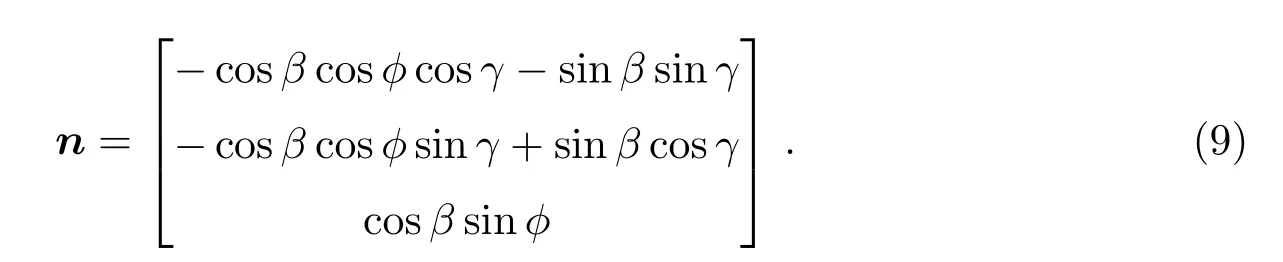
由拉格朗日摄动运动方程可知,轨道根数i、ω只被垂直于轨道面摄动力的作用影响,其余4个轨道根数只受轨道面内摄动力的影响(ω会因为Ω的变化而产生一定的变化).太阳帆控制类型有3种,一是保持在轨道面内一定的控制力的作用,二是保持垂直于轨道面的控制作用,三是保持垂直于光线照射的方向(以免光压成为破坏伴飞轨道的摄动力).

所需的控制力为u,通过矩阵旋转能够得到u在o1−x1y1z1坐标系中的表达式,如将o−xyz的坐标原点转移到o1点,角ζ表示ox轴与平面o1−x1y1的夹角,那么旋转矩阵为:

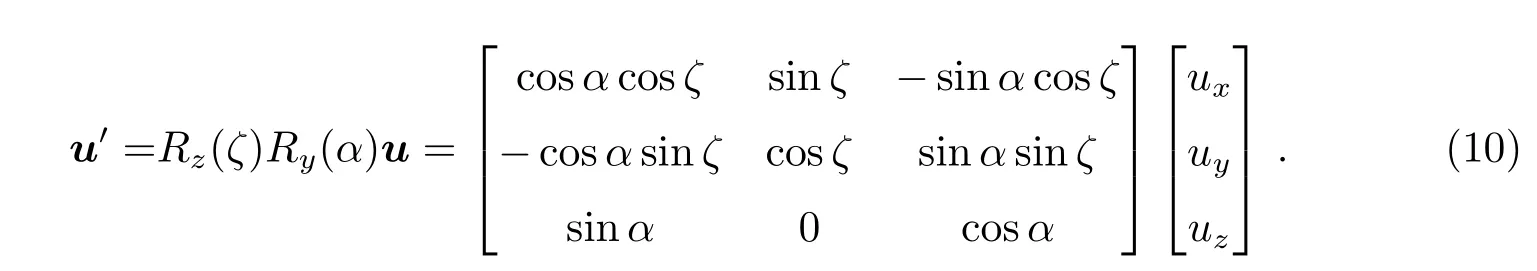
在伴飞卫星飞行过程中,α变化比较慢,ζ随着轨道的真近点角的增加做周期性变化.在轨道面内控制时,uz=0,此时u′满足:

要利用太阳帆进行轨道控制,就要求太阳帆的法线方向与控制力方向相反,即要满足:

将(10)式和(11)式代入(12)式后可以得到需要控制的角度ϕ、β满足的条件:

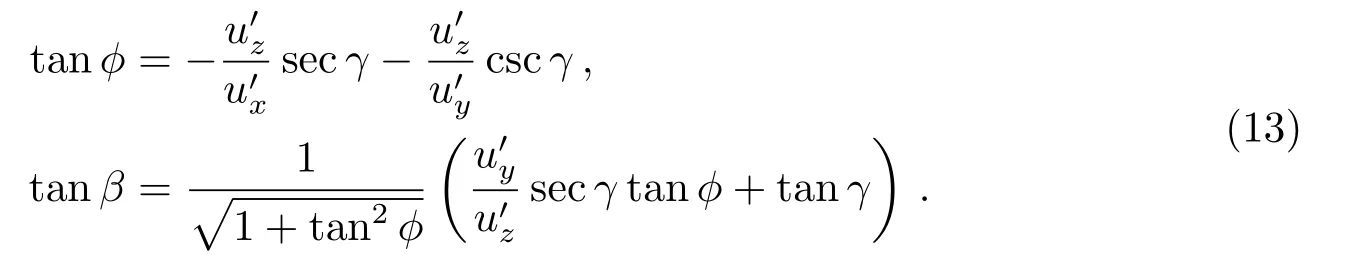
当太阳光压不能提供控制力时,需要将太阳帆平行于太阳光照射方向,此时:

其中

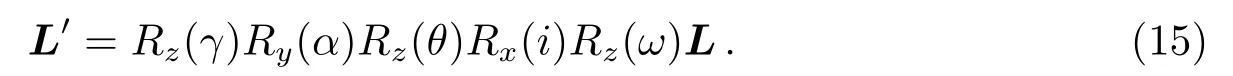
将(10)式和太阳光照方向矢量的表达式代入(15)式中,可以得到两个角度量之间的关系:

确定需要的控制力之后通过(13)式或者(16)式来控制太阳帆,就能够实现伴飞卫星的轨道控制.

3.2 初始轨道和控制系统设计

伴飞卫星受到摄动力的作用,会逐渐偏离原来的轨道,造成伴飞轨道的破坏.其中非球形引力摄动和日月第三体引力摄动属于保守力摄动,存在摄动势函数,通过初始轨道根数调整能够消除保守力摄动长期项的影响.在主星的LVLH坐标系下,摄动影响最大的是沿迹方向的误差.根据(7)式,要消除沿迹方向上的摄动,必须满足:

要满足(17)式,要求式中左边的初始状态均为0,并且变化率为零.定义两个变量:

令保守摄动平均化之后的势函数为R(a,e,i),根据拉格朗日摄动运动方程,可以得到和表达式:

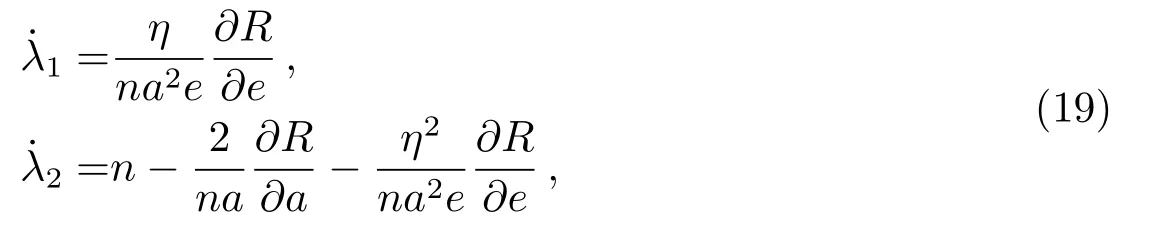
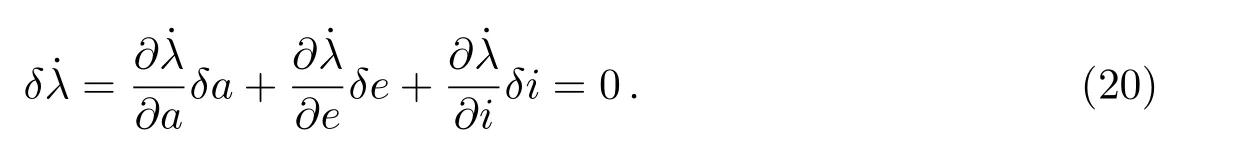
令差分值δ˙λ=0就可以消除保守力摄动长期项造成伴飞轨道y方向上的长期漂移.在所有的长期项中,影响最大的是非球形引力摄动J2项的影响.只考虑J2项作用时,初始轨道根数要满足的条件可以简化为:

应用此式作为初始轨道的限制条件,更高的精度要求可以用(20)式作为限制条件.

通过(2)式可得,在主星LVLH坐标系中,伴飞卫星的位置矢量在ox和oy方向上是相互耦合的,在oz方向上是独立的.因此,可以将整个伴飞轨道的控制系统分开.其中ox和oy方向是二维的非线性控制系统,oz方向是一维的非线性控制系统.

在实行ox和oy方向控制时,太阳帆不提供oz方向的控制力;在实行oz方向控制时,在ox和oy方向上均不提供控制力.在控制过程中,以ox和oy方向控制为优先控制,当ox和oy方向控制因为几何角度原因或者已经完成控制时,实行oz方向控制.由于太阳帆能够提供的摄动加速度并不很大,这种方法能够节省整个控制过程需要的时间.针对ox和oy方向控制应用滑膜控制方法设计一种控制策略.定义误差函数e为:

变结构控制是一种控制系统的设计方法,适用于线性及非线性系统,包括控制系统的调节、跟踪、自适应及不确定等系统.它具有一些优良特性,尤其是对加给系统的摄动和干扰有良好的自适应性.滑膜控制是一种特殊的变结构控制,本质上是一类特殊的非线性控制,且非线性表现为控制的不连续性.这种控制策略与其他控制的不同之处在于系统的结构并不固定,而是可以在动态过程中,根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化,迫使系统按照预定滑动模态的状态轨迹运动.由于滑动模态可以进行设计且与对象参数及扰动无关,这就使得滑膜控制具有快速响应、对应参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点.滑膜变结构控制的原理,是根据系统所期望的动态特性来设计系统的切换超平面,通过滑动模态控制器使系统状态从超平面之外向切换超平面收束.由于系统的特性和参数只取决于设计的切换超平面,而与外界干扰没有关系,所以滑膜变结构控制具有很强的鲁棒性.

当主星的轨道为椭圆轨道时,描述伴飞卫星的动力学系统为典型的非线性系统.在没有摄动力影响时,动力学系统在一定条件下是周期稳定的.周期稳定的前提为主星和伴飞卫星的轨道半长径完全相同.此时系统对初始的运动状态极为敏感,任何一个微小的轨道半长径的偏差均会引起稳定性的破坏.此外各种不同的摄动作用也会使得这种非线性系统无法自己保持稳定.因此必须对系统进行控制才会确保系统稳定.通过观测系统得到伴飞卫星和主星的运动状态(包括绝对运动的速度时间分量和相对运动的速度时间分量),为伴飞控制系统的状态变量.滑膜面为要求系统保持的状态的超平面(使得误差为0).控制调整后的伴飞系统的运动状态为输出量.控制系统的目标为使得系统的状态变量与定义的超平面重合.定义滑膜面为:

其中ν=diag[ν1,ν2]为常数对角矩阵,令控制力为:

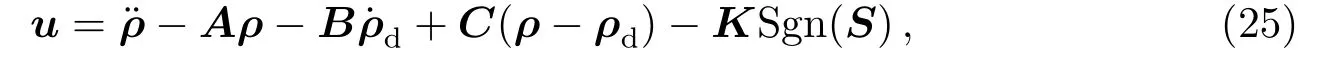
其中K=diag[K1,K2],并且有|Ki|＞|d1|和|K2|＞|d2|,K为控制系统需要对状态变量提供的控制变量(控制力)的大小的最小值.C的表达式为:

将(25)式代入(4)式,经过化简可以得到:

其中D为各种摄动力之和.系统的李雅普努夫函数(Lyapunov function)是:

其导数为:

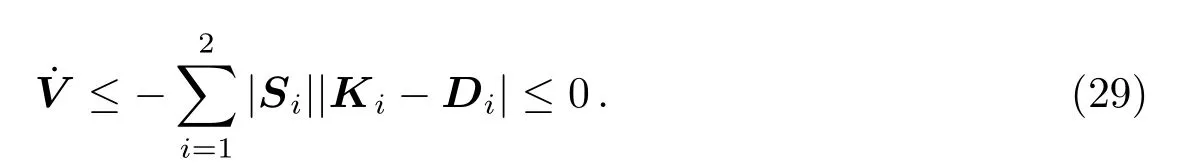
满足(29)式条件的控制力能够保证系统的稳定.在本文的条件下

其中umax为太阳帆能够提供的最大的推力值.在实际情况中,受到(12)式的限制,轨道面内的控制力由于几何关系的制约并不一定能够实时提供,也不能够维持整周的时间,有一定的间断性.

4 数值模拟

数值验证共有3个部分:第一为开环控制的伴飞卫星将相对轨道根数做对应的调整,对应实际的航天任务中的伴飞轨道重构;第二为加入人为的误差在滑膜控制系统的控制下将误差消除.这两部分均不考虑摄动作用的影响;第三部分检验在有摄动因素的影响时,利用滑膜控制系统保持伴飞轨道稳定.本文应用做数值运算的主星轨道的轨道半长径、轨道倾角和偏心率均与XMM-Newton卫星相同(如表1所示),另外3个轨道根数人为设定.伴飞轨道的相对轨道根数满足(21)式的限制条件.假设伴飞卫星的质量为80 kg,两个太阳帆的面积为4 m2.

图3～5表示应用太阳光压控制方法使得伴飞卫星的相对轨道根数发生变化的变化规律,初始时间为2015年1月1日0时.如图3所示,需要1次调整轨道半长径就能够增加或减少10 m,降低10 m需要的时间为0.075 d,增加10 m需要的时间为0.06 d.

表1 主星轨道根数Table 1 The orbital elements of the leading satellite

图3 伴飞卫星轨道半长径的调整,左图表示降低10 m的控制过程,右图表示增加10 m的控制过程.Fig.3 The adjustment of the semi-major axis of the follower.The left is the control of decreasing 10 m, the right is the control of increasing 10 m.

如图4所示,使得偏心率增加2×10−5需要时间为1.2 d,经过1次调整就能够达到目的,具体的控制时间大约从第0.3天开始,到第1.2天时结束.使得偏心率降低2×10−5需要时间大约为8 d.需要经过7次调整,每次调整经历的控制时间不同.第2次和第5次的调整经历时间最长,两次调整均能够使得轨道偏心率降低5×10−6以上,最后控制在第8天时间最终完成.

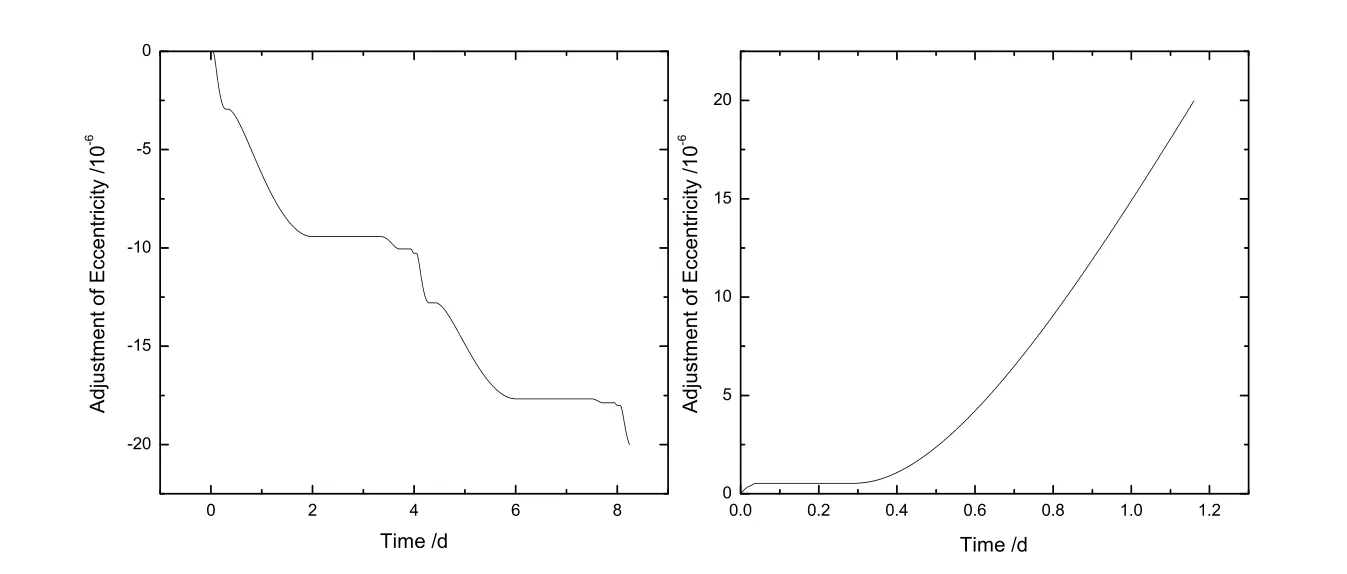
图4 伴飞卫星轨道偏心率调整.左图表示降低2×10−5的控制过程,右图表示增加2×10−5的控制过程.Fig.4 The adjustment of eccentricity of the follower.The left is the control of decreasing 2×10−5,the right is the control of increasing 2×10−5.

如图5所示,使轨道倾角增加1′′需要时间为8 d,控制经过3次调整过程.控制开始的时间恰好能够进行第1次调整,经历时间大约为2 d,轨道倾角增加大约0.4′′;第2次调整时间为第4天到第6天,轨道倾角增加0.5′′,最后第8天时第3次调整达到最终增加1′′的目标.降低1′′需要时间为11 d,整个控制过程同样经历3次调整过程.第1次调整从第3天开始,调整时间大约为1 d,轨道倾角降低0.2′′;第2次调整从第7天开始,经历时间稍大于1 d,轨道倾角降低0.3′′;第3次调整从第10天开始,经历2 d,轨道倾角降低0.5′′.调整所需要的时间与轨道的初始状态和太阳的位置关联很大.

图5 伴飞卫星轨道的轨道倾角调整,左图表示降低1′′的控制过程,右图表示增加1′′的控制过程.Fig.5 The adjustment of inclination of the follower.The left is the control of decreasing 1′′,the right is the control of increasing 1′′.

图6表示误差消除的状况,初始时间同样为2015年1月1日0时.在x方向和z方向分别添加10 m的误差,从图中可以得出,沿x方向上10 m的误差能够在2 h内消除,沿z方向10 m的误差能够在5 h内消除.

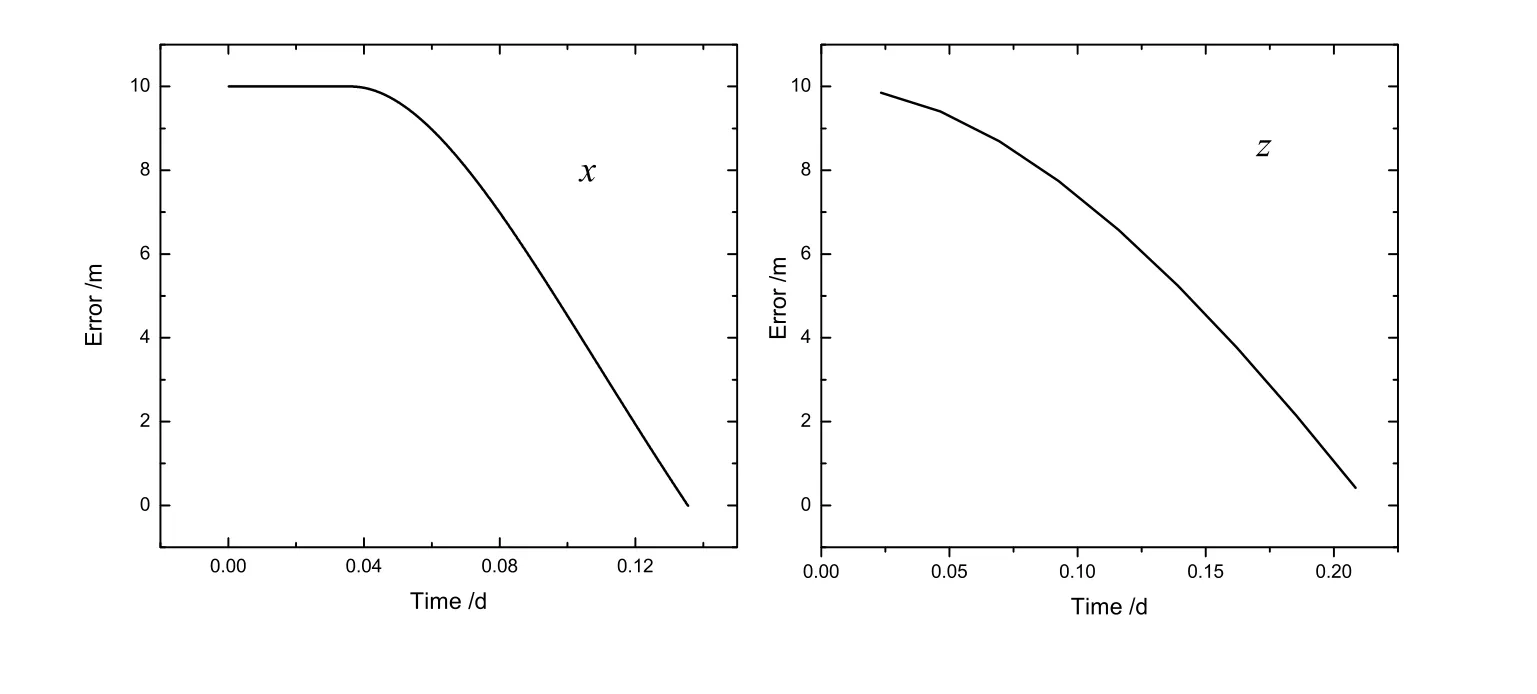
图6 伴飞卫星轨道x(左)和z(右)方向误差消除Fig.6 The error elimination along the x(left)and z(right)directions

图7表示初始时间不同(太阳位置不同)时应用太阳光压辐射控制系统对于x方向上误差修正的能力.时间跨度为2014年整年,横坐标表示调整开始时的天数,纵坐标表示10 d内能够消除的x方向上误差的大小.从图中可得,10 d内能够消除的误差最大可达2 500 m,最小不到30 m.

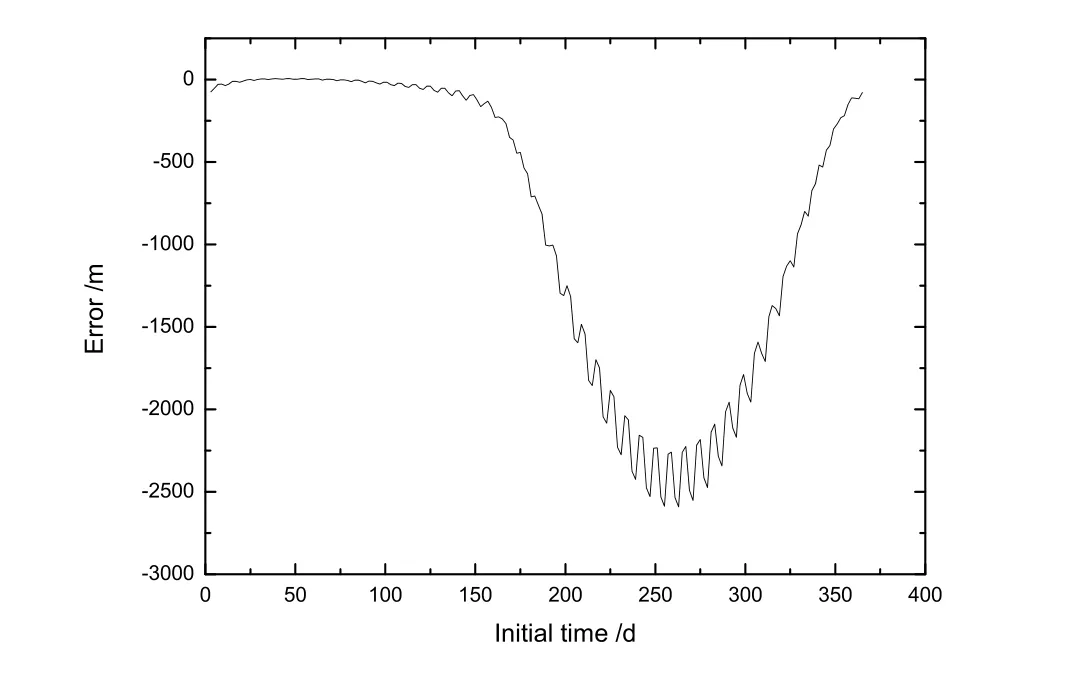
图7 伴飞卫星轨道x方向上初始时间不同时10 d内的误差消除能力Fig.7 The error elimination ability along the x direction in 10 days with di ff erent initial epoch

图8表示考虑20阶地球非球形引力摄动和日月第三体引力摄动的影响.在本文的设计中轨道演化10 d的误差保持,可见在一定时间范围内,沿各个方向上的误差会出现波动.经过一段时间,误差会被控制系统消除,在整个控制过程中,误差能保持在5 m以下.在x、y方向上的误差维持得比较小,在z轴上的误差比较大,但是仍然能够维持在米级.

图8 伴飞卫星轨道的保持过程中3个方向上的误差变化Fig.8 The errors along the 3 directions during the formation maintenance

5 总结与展望

本文提供了一种能够控制大偏心率伴飞轨道的方法.通过调整太阳帆的指向,将太阳光压辐射产生的作用力作为控制力,能够成功达到控制目的.经过数值验证,在卫星飞行一周的时间里,能够进行10 m级的轨道误差修正,在考虑非球形引力摄动时能够使伴飞轨道误差维持在5 m以内.

这种方法仍旧有一定的局限性,比如控制力的方向受到伴飞卫星和太阳的相对位置的局限,控制力的大小受到太阳帆的面积的局限,以及调整相对位置时的能量消耗与太阳能电池的能量供应关系等.要克服这些局限性并实际应用,仍需要进一步研究.

[1]Alfriend K,Schaub H.JASS,2000,48:249

[2]Liu H,Li J F.AerST,2006,10:636

[3]Kumar K D,Misra A K.AcAau,2014,102:341

[4]Suchandt S.AdSpR,1997,20:575

[5]胡寿村,赵玉晖,季江徽,等.天文学报,2015,56:154

[6]Hu S C,Zhao Y H,Ji J H,et al.ChA&A,2015,39:512

[7]甘庆波,张扬,朱正帆,等.天文学报,2014,55:476

[8]Gan Q B,Zhang Y,Zhu Z F,et al.ChA&A,2015,39:341

[9]Vokrouhlicky D,Farinella P,Mignard F,et al.A&A,1993,280:295

[10]Smimov G V,Ovchinnikov M,Guerman A.AcAau,2007,61:724

[11]罗宇阳.椭圆轨道卫星编队构型设计与姿态协同控制技术研究.上海:上海交通大学,2012

[12]张玉锟.卫星编队飞行的动力学与控制技术研究.长沙:中国人民解放军国防科学技术大学,2002

Orbit Control of Fly-around Satellite with Highly Eccentric Orbit by Using Solar Radiation Pressure

HOU Yong-gang1,2,3ZHAO Chang-yin1,2ZHANG Ming-jiang1,2SUN Rong-yu1,2
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjng 210008)
(2 Key Laboratory of Space Object and Debris Observation,Chinese Academy of Sciences, Nanjing 210008)
(3 University of Chinese Academy of Sciences,Beijing 100049)

The method of controlling highly eccentric fly-around orbit using the solar wing is designed in this paper.The formation is maintained by controlling the follower. The in-plane and the out-of-plane control are separated.The follower is rotating around the inertial principal axis with a constant angular velocity.The controlling of the angular between the solar wings and satellite body is obtained.The orbit is controlled by adjusting the geometrical orientation.The in-plane control is prior to the out-ofplane control.The out-of-plane control force is applied when the error of in-plane is eliminated or the in-plane control force can not be supplied.Three di ff erent kinds ofnumerical simulations including the orbit recon figuration,the error elimination,and the orbit maintenance are performed.It is shown that the method can keep the error less than 5 m,and it is feasible for the space formation.

space vehicles,celestial mechanics,methods:numerical

P135;

:A

10.15940/j.cnki.0001-5245.2016.01.006

2015-04-02收到原稿,2015-05-26收到修改稿

∗国家自然科学基金项目(11125315,11173056)资助

†shanda.hou@163.com