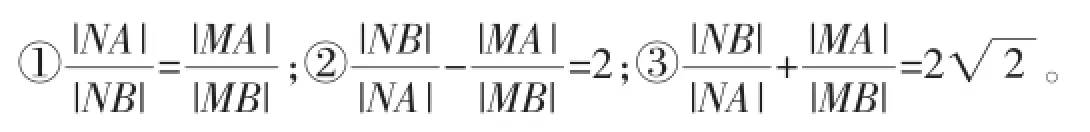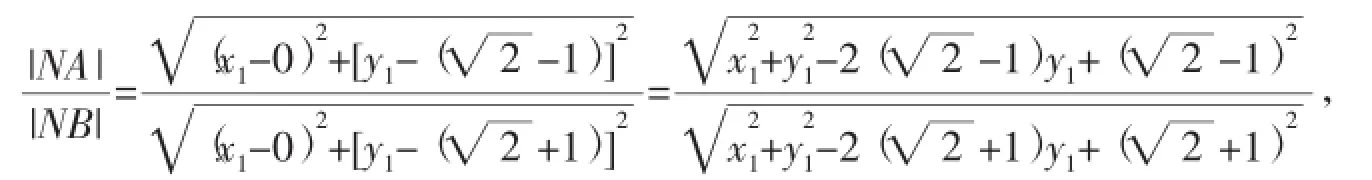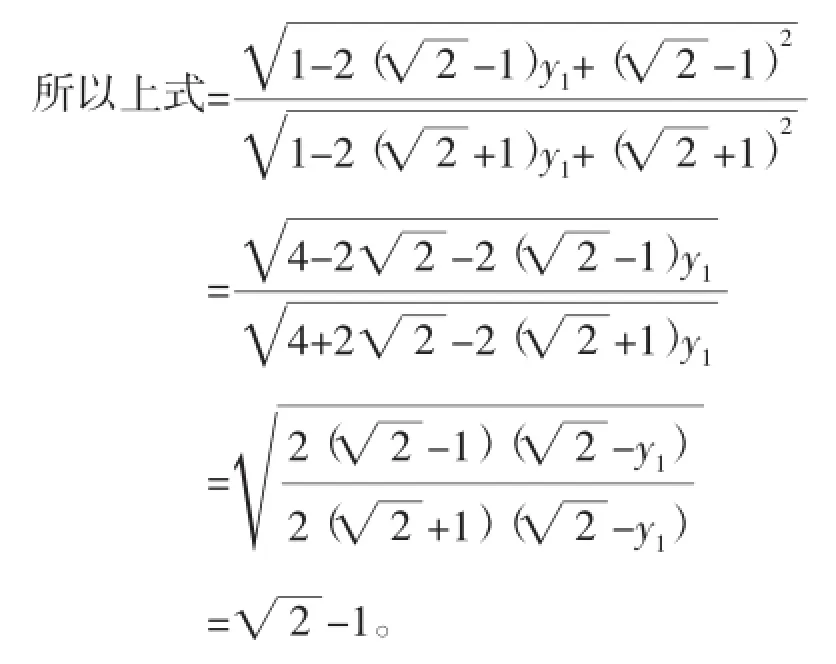有趣的阿波罗尼斯圆

安徽省铜陵一中　陈良骥



有趣的阿波罗尼斯圆

安徽省铜陵一中陈良骥

引例设A（-c，0）、B（c，0）（c>0）为两定点，动点P到点A的距离与到点B的距离之比为定值a （a>0），求点P的轨迹。

（1）当a=1时，上式化简为x=0，此时点P的轨迹是y轴，即线段AB的中垂线。

引例的解析过程实质上证明了如下定理：平面内到定点A、B的距离之比等于常数a（a≠1）的动点轨迹是一个圆。这个定理是由古希腊的数学家阿波罗尼斯首先提出的，所以我们把这个圆称为“阿波罗尼斯圆”，把这个结论称为“阿波罗尼斯轨迹”。

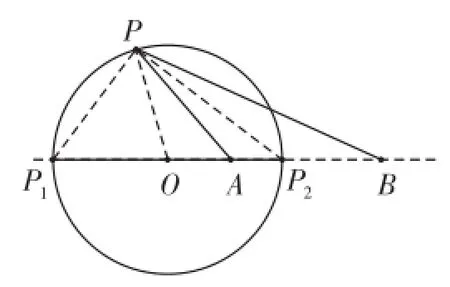
除了解析法，上述定理也可以利用几何法证明，过程如下：

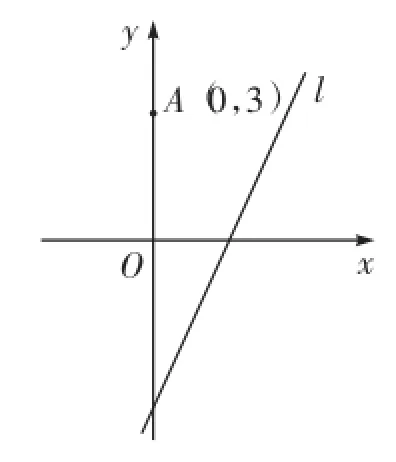
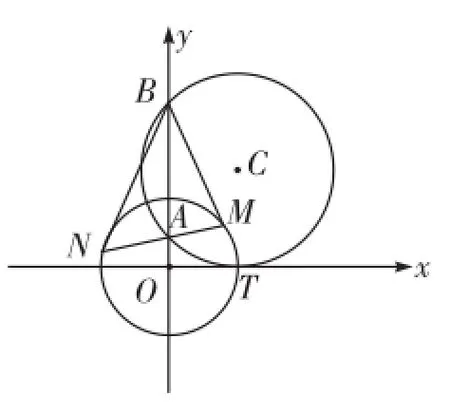
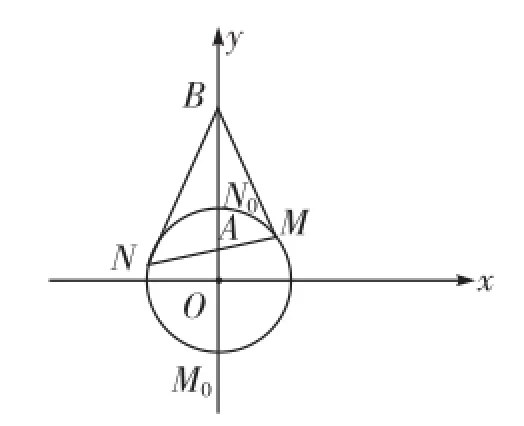
如图，不妨设0

（1）在圆O上任取一点P，若P∈AB，则P为P1或P2，显然满足若P埸AB，则△P OA∽△BOP，即，即圆O上每一点P都满足

由以上可知，平面内到定点A、B的距离之比等于常数a（a≠1）的动点轨迹是以P1P2为直径的圆。

高考中的阿波罗尼斯圆近年来，以阿波罗尼斯圆为背景的相关问题备受高考命题者的青睐。从相关试题对阿波罗尼斯圆的考查方式和角度来看，主要分为以下几类。

1.直接考查轨迹

例1（2013年江苏卷）如右图，在平面直角坐标系xOy中，已知点A（0，3），直线l：y=2x-4。设圆C的半径r=1，圆心在l上。

（1）若圆心C也在直线y=x-1上，过点A作圆的切线，求切线的方程。

（2）若圆C上存在点M，使|MA|=2|MO|，求圆心C的横坐标a的取值范围。

解析（1）易知C（3，2）。设切线方程为y=kx+3，则由题意得，解得k=0或，即切线方程为

（2）设M（x，y），一方面由|MA|=2|MO|，求得点M（x，y）满足x2+（y+1）2=4，即点M在一个新圆E（圆心E（0，-1），半径R=2）上，

另一方面，点M还在圆C上，所以圆C与圆E有公共点，

2.与解三角形结合

解析不妨设A（0，0），B（2，0），C（x，y）（y≠0），由求得点C的轨迹方程是x2+y2-8x+8=0（y≠0），即点C在圆心为（4，0），半径为的圆上运动，所以点C到AB边距离的最大值是，于是△ABC面积的最大值为

3.突出比例特征

例3（2014年湖北卷）已知圆O：x2+y2=1和点A（-2，0），若定点B（b，0）（b≠-2）和常数λ（λ>0）满足：对圆O上任意一点M，都有|MB|=λ|MA|，则

（1）b=＿＿。（2）λ=＿＿。

解析易知λ≠1。设M（x，y），由|MB|=λ|MA|，知化简得

与方程x2+y2=1比较知

例4（2015年湖北卷）如图，圆C与x轴相切于点T（1，0），与y

轴正半轴相交于A、B两点（B在A的上方），且|AB|=2。

（1）圆C的标准方程为＿＿。

（2）过点A任作一条直线与圆O：x2+y2=1相交于点M、N，下列三个结论：

其中正确结论的序号是＿＿。（写出所有正确结论的序号）

（2）方法一：设N（x1，y1），易知

方法二：注意到圆O：x2+y2=1与y轴交于点N0（0，1），M0（0，-1），且，由阿波罗尼斯圆的几何法证明过程知，以N0（0，1），M0（0，-1）为直径的圆上的每一点都符合到A、B距离之比为定值，所以，所以可以判断①②③都正确。