基于图论的平原河网区水系连通性评价
——以常熟市燕泾圩为例
陈 星,许 伟,李昆朋,张其成,林 松
(1.河海大学水文水资源学院,江苏 南京 210098; 2.南京水利规划设计院有限责任公司,江苏 南京 210006)
基于图论的平原河网区水系连通性评价
——以常熟市燕泾圩为例
陈星1,许伟1,李昆朋2,张其成1,林松1
(1.河海大学水文水资源学院,江苏 南京210098; 2.南京水利规划设计院有限责任公司,江苏 南京210006)
摘要:探讨河网连通性内涵,将河网连通性分为结构连通性和水力连通性;基于图论,将河网概化为图模型,以图模型可达性特征,利用Matlab对河网的结构连通性做出定量评价。考虑不同河道之间输水能力差异性,用河道水流阻力的倒数作为水流流通度,通过ArcGIS构建权值邻接矩阵,通过Matlab实现对河网的水力连通度的定量评价。以常熟市燕泾圩平原河网为例,对水系规划前后的河网连通性进行定量评价,结果表明,规划后的河网结构连通性和水力连通性均有所增加。
关键词:平原河网;图论;结构连通性;水力连通性;水流阻力
河网是区域水资源的载体和水循环的基础,其连通格局影响水安全保障能力、水资源配置能力以及水循环能力。在城市化进程中,河道被占用情况屡见不鲜,大量河道被填埋,河道堵塞、过水不畅,平原河网区水系连通性降低,区域水循环受到影响[1]。随着经济社会对水资源有着更高、更新的要求,水系连通性对城市的发展有着更重要的意义。在探索水系连通性分析方法的过程中,国外做了不少的工作,但是开展平原河网区水系连通性定量分析的方法较少[2];国内较重视河网水系连通性研究,但处于初期研究阶段,专家学者仍在努力构建平原河网区水系连通性评价体系[3]。
目前,水系连通性分析方法较多,主要有图论、复杂网络理论、水文模型、景观生态学等。平原河网水流流向多变,河底比降较小,不利于模型模拟。图论以其对水流单向流、双向流的双重性考虑,适合用于平原河网水系连通性定量评价。近期,图论在水系连通性评价上的应用得到逐步的发展。邵玉龙等[4]把水系中节点之间的连通度平均值视为水系整体连通度;徐光来等[5]结合图论与水流阻力分析河网连通性;杨晓敏[6]采用图论方法评价胶东地区的水系连通性。笔者根据水系连通性的内涵,分类应用图论,并进行了改进。
1河网水系连通性评价
1.1水系连通性内涵
水系包含两个基本要素[7-9]:承载水流的相互交织在一起的河道;能够提供资源的不断循环的水流。在判断水系连通性的时候,需要考虑这两个方面。河道是过水通道,它们之间是否连通直接影响水系结构连通性,河网系统中河道交汇的越多、越复杂,河网系统结构连通性越好、承载能力越强,而其遭到破坏后恢复能力就越差。城市化过程中,部分河道束窄、河床淤积,导致河道过水能力大大下降,河道连而不通。河网系统中的水力连通性受到河道的长度、宽度、糙率、河底比降等的影响,不同河段的流速具有差异性。河网系统中水系的两个不同方面——结构连通性、水力连通性,结构连通性是基础,水力连通性是目标,水力连通性受到结构连通性的制约。在结构连通性没有保证的前提下讨论水力连通性,是忽略水系结构的功能。河网系统的水系连通性评价中,结构连通性先于水力连通性,要先评价是否有相互连通的河道给水流提供过水通道,然后再评价水力连通性。
1.2河网水系模型概化
图论中的“图”并不是通常意义下的几何图形或物体的形状图,而是以一种抽象形式来表达事物之间相互联系的数学模型。为实际对象建立图模型后,可以利用图的性质进行分析[10]。河网水系模型概化中,需要将水系中的不同节点利用图论中的相关元素进行表征。河道通过边(E1、E2、E3、E4、E5、E6、E7)来表示,河流汇合处、边界条件和蓄水工程用点(V1、V2、V3、V4、V5、V6)来表示,将河网水系概化成图模型(图1)[11]。

图1 河网水系模型概化
概化模型简化写成二元素图G=(V,E),V表节点集合,E表示边集合。图G=(V,E)所表达边或点之间的关系与概化模型图是等价的。河网结构连通性不考虑水流因素,所以这里的河网水系概化图模型是无向图,其中点与点之间的关系通过图的邻接矩阵表示(图1(a))。河网系统中水力连通性考虑水流因素,水流有流向和流速的特征,其河网水系模型概化比结构连通性的概化复杂。由于水流是有向的,所以概化出的图是有向图(图1(b))。
图G=(V,E)中V有n个元素,邻接矩阵就为n阶矩阵,记作A=(aij)n×n。邻接矩阵根据图G=(V,E)中点与点之间的关系建立[10-11]:
对于图1,通过ArcGIS中拓扑关系建立的邻接矩阵为
1.3河网水系结构连通性评价
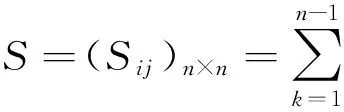
利用图的连通性定义,河网水系概化模型图分为连通和不连通两种。从连通图中去掉一些边后,图可能不再是连通的。两个连通图去掉相同的边数之后,其中一个图已经是不连通的,而另一个还是连通的,仍然连通的图原图结构连通性强,所以这里引入连通度的概念,图的连通度就是连通图删去最多边数使图恰好变成不连通图,记此边数为连通度(以D来表示)。以连通度判断图连通程度,连通度越大,连通性越强[6,11]。
1.4河网水系水力连通性评价
对于水流的流速特征通过给概化模型图中的边赋值来体现,即边的权值ω越大,流通性越好。按河道水流阻力确定权值时,需要考虑水流阻力与流速关系呈负相关。平原河网中处于不稳定流的情况下,流量由节点间的水位差决定,水流阻力受到河道形状和摩擦力影响。平原河道河床坡度极小,可以忽略不计,定点间河道的水流阻力H[5,12]可表示为
(1)
式中:n为河道糙率;b为河道宽度,m;h为河道水深度,m;m为河道边坡系数。矩形河道的水流阻力计算中,m=0。相邻节点间的边权值ω用水流阻力的倒数表示,即ω=1/H。
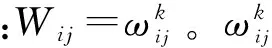

图2 图的边与点的示意图
图2中V1到V3有:①V1—E1—E3—V3;②V1—E2—E3—V3和③V1—E4—V33条路径,其中E1=0.3,E2=0.2,E3=0.1,E4=0.2。以乘法矩阵时:M13=max{E1×E3,E2×E3,E4}=0.2。为改进不相邻节点间权值计算的合理性,通过比较得到各路径下的权值Wl1=0.1,Wl2=0.1,Wl3=0.2。考虑水流在分流后汇合,流量会重新叠加,重复利用E3的两条路径同时生效。因此,V1到V3权值通过3条路径累加得到M13=Wl1+Wl2+Wl3=0.4。

2实例分析
2.1研究区概况
以常熟市燕泾圩为例,分析规划前后连通性情况。燕泾圩位于常熟市虞山镇,水面积1.07 km2,水面率11.3%。圩内主要骨干河道有4条:斜桥塘、燕泾、洋塘、和尚泾。圩内河网分布不均,城市化建设阻断原有河道,破坏了水系的结构连通性,影响水力连通性。圩外引水河道为元和塘,排水河道为莫城河。
水系连通:恢复原有的连通河道,斜桥塘与燕泾之间的连通河道(V17—V18)长750 m,河道规模为:河口宽10~20 m,河底宽5~10 m,底高程0.5 m;燕泾与洋塘之间的连通河道(V17—V5)长为770 m,河口宽10 m,河底宽5~10 m,底高程0.5 m。结合河道的现状条件,恢复和尚泾与其南部河道(V10—V12)的连通性,增加该区域的水体流动性。
河道拓浚与疏浚:燕泾圩内现状主要引排水河道规模较大,经过规划连通后,在引水量充足的情况下可以满足圩区内的供水需求,主要对斜桥塘(V1—V18—V3—V6)、燕泾(V2—V17—V3)等主要河道进行疏浚。规划前后水系规划图见图3中(a)和(b)。

图3 规划前后水系概化
2.2水系规划前后的结构连通性评价
河网结构连通性不考虑河道中水流流向,概化出来的图是无向图。常熟市燕泾圩区规划前概化图有16个节点、21条边,规划后概化图有18个节点、26条边。通过ArcGIS拓扑关系得到概化图邻接矩阵W:
通过Matlab编程判断规划前后概化图是连通的,且规划前的连通度D是6、规划后的连通度D为9,连通度增加了50%。
2.3水系规划前后的水力连通性评价
与结构连通性不同,河网水系的水力连通性概化成有向图,根据实测的水流方向确定各条边的方向。由《常熟水系调控规划》获得河道的宽度、深度、边坡和糙率。圩区的河道较小,边坡取值为1∶3。糙率的取值以河道的实际特性来定,对于河床较平整、河道顺直、断面规则、岸壁为土质或石质的断面,糙率值取0.025;对于水流不够通畅,岸壁为黄土质并且长有杂草的断面,糙率值取0.027;对于河道弯曲,岸壁为土质,且杂草稠密的断面,糙率值取0.03。河节点之间的权值通过式(1)计算,不直接相邻的节点间的权值由不同路径最小权值边叠加确定,用ArcGIS拓扑关系建立权值邻接矩阵M。
节点V11、V16处于河网的出口处,连通度与下游河道有关,属于圩区外围,不做连通度计算。规划前河网水系中节点V1、V2、V4等处流通度较大,V9、V12、V13、V14、V15等节点流通度相对较小。规划后河网水系中V1、V2、V4、V7、V10、V17、V18流通度较大,V9、V12、V13、V14、V15流通度较小,增加的节点V17、V18连通度分别为3.52、3.41(图4)。

图4 规划前后顶点流通度柱状图
为促进圩区内的水体循环,燕泾圩水系规划增加主要引水河道斜桥塘、燕泾及洋塘之间的联系。与规划前河网水系节点水流流通度相比较,规划后各节点的水流连通度增加6.7%~42.5%。规划前河网流通度为2.688,规划后河网流通度为3.19,增加了18.7%。规划中局部河道的连通与拓浚,对圩区河网流通度都有影响,增加了河网整体的水力连通性。
3结论
基于图论评价河网连通性,要考虑水流的流向。本文选取的实例流向是固定的,概化的图模型中方向固定。对于水流流向多变的河网,同样可以采用图论方法评价。流向不稳定区域概化出的图模型具有双向性,评价水力连通性时,需要考虑图中的双向性特征建立邻接矩阵,具体计算步骤不变。
参考文献:
[ 1 ] 陈云霞,许有鹏,付维军.浙江沿海城镇化对河网水系的影响[J].水科学进展,2007,18(1):68-73.(CHEN Yunxia,XU Youpeng,FU Weijun.Influences of urbanization on river network in the coastal areas of East Zhejiang Province[J].Advances in Water Science,2007,18(1):68-73.(in Chinese))
[ 2 ] 王柳艳.太湖流域腹部地区水系结构、河湖连通及功能分析[D].南京:南京大学,2013.
[ 3 ] 孟祥永,陈星,陈栋一,等.城市水系连通性评价体系研究[J].河海大学学报(自然科学版),2014,42(1):24-28.(MENG Xiangyong,CHEN Xing,CHEN Dongyi,et al.Evaluation system of urban water system connectivity[J].Journal of Hohai University(Natural Sciences),2014,42(1):24-28.(in Chinese))
[ 4 ] 邵玉龙,许有鹏,马爽爽.太湖流域城市化发展下水系结构与河网连通变化分析:以苏州市中心区为例[J].长江流域资源与环境,2012,21(10):1167-1172.(SHAO Yunlong,XU Youpeng,MA Shuangshuang.Water system structure and network connectivity change analysis influenced by urbanization development of Taihu City watershed in Suzhou downtown area[J].Resources and Environment in the Yangtze Basin,2012,21(10):1167-1172.(in Chinese))
[ 5 ] 徐光来,许有鹏,王柳艳.基于水流阻力与图论的河网连通性评价[J].水科学进展,2012,23(6):776-781.(XU Guanglai,XU Youpeng,WANG Liuyan.River connectivity evaluation based on graph theory and resistance to water-flow[J].Advances in Water Science,2012,23(6):776-781.(in Chinese))
[ 6 ] 杨晓敏.基于图论的水系连通性评价研究:以胶东地区为例[D].济南:济南大学,2014.
[ 7 ] 茹彪,陈星,张其成,等.平原河网区水系结构连通性评价[J].水电能源科学,2015,31(5):9-12.(RU Biao,CHEN Xing,ZHANG Qicheng,et al.Evaluation of connectivity of river network in plain area[J].Hydroelectric Energy,2015,31(5):9-12.(in Chinese))
[ 8 ] 王中根,李宗礼,刘昌明,等.河湖水系连通的理论探讨[J].自然资源学报,2011,26(3):523-529.(WANG Zhonggen,LI Zongli,LIU Changming,et al.Theoretical research on river-lake system connectivity[J].Journal of Natural Resources,2011,26(3):523-529.(in Chinese))
[ 9 ] 张欧阳,熊文,丁洪亮.长江流域水系连通特征及其影响因素分析[J].人民长江,2010,41(1):1-5,78.(ZHANG Ouyang,XIONG Wen,DING Hongliang.Analysis of water system connectivity and its influence factors in the Yangtze River Basin[J].Yangtze River,2010,41(1):1-5,78.(in Chinese))
[10] 王海英,黄强,李传涛,等.图论算法及其MATLAB实现[M].北京:航空航天大学出版社,2010.
[11] 赵进勇,董哲仁,翟正丽,等.基于图论的河道-滩区系统连通性评价方法[J].水利学报,2011,42(5): 537-543.(ZHANG Jinyong,DONG Zheren,ZHAI Zhengli,et al.Evaluation method for river floodplain system connectivity based on graph theory[J].Journal of Hydraulic Engineering,2011,42(5): 537-543.(in Chinese))
[12] POULTER B,GOODALL J L,HALPIN P N.Applications of network analysis for adaptive management of artificial drainage systems in landscapes vulnerable to sea level rise[J].Journal of Hydrology,2008,357(3/4): 207-217.
Evaluation of plain river network connectivity based on graph theory:a case study of Yanjingwei in Changshu City
CHEN Xing1, XU Wei1, LI Kunpeng2, ZHANG Qicheng1, LIN Song1
(1.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China;2.NanjingWaterPlanningandDesigningInstituteCo.Ltd.,Nanjing210006,China)
Abstract:The implications of river network connectivity are discussed in this paper. River network connectivity is classified into two types: structural connectivity and hydraulic connectivity. Based on the graph theory, the river network is generalized as a graph model. According to the reachability characteristic of graph models, the river network’s structural connectivity is quantitatively evaluated by Matlab. With consideration of the difference in water conveyance capacity between rivers, the reciprocal of the resistance of river flow is regarded as the flow distribution, the adjacency matrix is built with ArcGIS, and the river network’s hydraulic connectivity is quantitatively evaluated with Matlab. A case study of the Yanjingwei Plain River Network, in Changshu City was conducted. The river network connectivity before and after river system planning was quantitatively evaluated. The results show that both the structural connectivity and the hydraulic connectivity of the river network increased after planning.
Key words:plain river network; graph theory; structural connectivity; hydraulic connectivity; flow resistance
DOI:10.3880/j.issn.1004-6933.2016.02.006
基金项目:江苏省科技支撑计划(BE2011697);苏州市水利科技计划(2014-07-06)
作者简介:陈星(1980—),女,讲师,博士,主要从事水文、水环境保护研究。E-mail:chengxing@hhu.edu.cn
中图分类号:TV212
文献标志码:A
文章编号:1004-6933(2016)02-0026-04
(收稿日期:2015-12-28编辑:彭桃英)

