分形理论在断裂与矿产关系研究中的应用
李 飞, 刘国生, 周庆卫, 赵光宝
(合肥工业大学 资源与环境工程学院,安徽 合肥 230009)
分形理论在断裂与矿产关系研究中的应用
李飞,刘国生,周庆卫,赵光宝
(合肥工业大学 资源与环境工程学院,安徽 合肥230009)
摘要:文章以招远金矿矿集区为例,在对研究区断裂与矿产分布关系的详细野外调查基础上,运用分形理论的盒维数法对区内断裂构造体系进行了分形研究,并对断裂与矿产分布的关系及矿产赋存规律进行了总结。通过分形计算,获得招远地区断裂构造总体的分维值D=1.48,地质体连通性断裂分维值临界值D为1.22~1.38。不同走向断裂的分维值:NNE向D=1.223,NE向D=1.194,近EW向D=0.864,NW向D=0.781。上述结果表明NNE、NE向断裂系统复杂程度较高,该方位断裂对矿产的控制强度大。这与区内大型、超大型金矿床多沿着NNE向断裂分布,尤其是招平、焦家断裂带,NNE向断裂起导矿、控矿作用这一地质事实相吻合,也反映出本区NNE、NE向断裂的拐点及其与不同方位断裂的交叉点的存在和发育程度影响着金矿床的分布。
关键词:分形理论;分维值;控矿断裂;金矿;招远
0引言
分形(Fractal)理论[1-4],是20世纪70年代中期由美籍数学家曼德勃罗(B.B.Mandelbrot)提出的,它是横跨自然科学、社会科学和思维科学的新理论,用分维的视角和数学方法研究和揭示复杂的自然现象和社会现象中所隐藏的规律性、层次性和标度不变性,为人们通过部分认识整体、从有限中认识无限提供了一种新的工具。而由1919年德国数学家Hausdorff提出的分形维数[5],是定量刻画分形特征的参数,是用来定量描述这种自相似性的参数。在断裂构造的研究中,分维值可以做到定量描述构造的复杂程度,分维值越高,构造越复杂,对矿床产出的影响越大,它是断层数量、规模、发育程度、组合方式的综合体现。近年来,分形几何学等非线性理论的发展及其在地质学中的广泛应用[5-6],为断裂构造空间分布和几何结构特征的定量表征提供了新的手段,同时也为断裂构造及其与金银矿床与矿点的空间分布关系研究提供了新的思路。
位于华北板块东部胶辽隆起区胶东半岛北部的胶东成矿带,是我国目前探明金储量最大和发现特大型矿床最多的地区。文献[7-8]通过对招掖金矿带内花岗岩与金矿化关系研究认为:花岗岩沿构造软弱带的侵位通道和先存的韧性剪切带是贯通深部流体的导矿构造,花岗岩类与围岩的接触带及其内部断裂和裂隙是有利的赋矿场所。文献[9]通过对玲珑—焦家地区金矿成矿构造体制的研究认为:控制石英脉型金矿和蚀变岩型金矿的成矿构造分属左旋走滑-正滑成矿构造系列和正滑-左旋走滑成矿构造系列。文献[10-13]对胶东矿集区构造演化与成矿系统动力学进行了研究,文献[14-16]从矿田构造方面对山东招远玲珑金矿形成机制开展研究,文献[17]则从金矿床地球化学角度探讨了招平断裂对金矿控制规律。
上述研究成果从大型矿床和大尺度方面探讨了NNE向主断裂对金矿床的控制规律。然而,对于区内所存不同尺度、不同方位的断裂对不同规模矿床的控制与影响,以及NNE向断裂区域空间分布规律、构造复杂程度及对矿床的控制规律尚有待做深入研究。本文以招远金矿区为例,应用分形理论计算区内断裂构造空间展布特征的分维值,进而确定区域内断裂构造的复杂程度及断裂的控矿特征与分维值的相关性,为进一步找矿勘探提供参考。
1分形几何计算在断裂中的应用
在成矿系统中,断裂构造起着重要的作用,不仅为成矿热液的运移提供通道,而且为矿体的赋存提供了空间。对金矿区断裂构造的研究,是进行成矿规律与成矿预测研究的重要内容。
断裂构造在平面上表现为一系列线状组合,从表面上看,这种分布是无规则的、混乱的,无法用传统的欧式几何学对断层的分布规律进行描述。但断裂构造系统在空间上具有自相似性,由此可将断裂构造当作分形体来研究,以断裂构造的分形维度来对断裂的空间规模和发育程度做定量的描述[18]。断裂的分维值与断裂构造的复杂程度成正比,分维值越大,断裂的空间分布越复杂,主断裂的分支断裂就越多,区域内断裂发育程度越高,越有利于成矿热液的运移和成矿元素的富集,越有利于矿床的形成。文献[19]分别从发育规模和形成年代对断裂进行了分析研究,研究结果表明,浅源断裂比深源断裂分维值高,老断裂分维值比新断裂分维值高。因为浅源断裂一般以密集分布的小规模断裂为主,而深源断裂一般发育为稀疏的韧性岩石圈断裂,在地表的破碎程度较低,分支断裂也较少,分维值较低;从断层形成的年代来看,一般老断层会受到改造,其发育程度一般较高,因此老断层的分维值比新断层大。
在断裂构造的分形结构特征与矿床的关系上,文献[20]应用分形几何理论对柴达木盆地北缘断裂体系的分布进行了定量研究,用盒计维数法计算分维值,并对该区油气聚集分布有利区进行了预测;文献[21]对桂东南地区断裂构造分形特征与金银成矿关系进行研究发现,区内金银矿化均落入分维高值区;文献[22]对西藏古堆—隆子地区断裂构造ETM遥感影像进行解译,发现分维值高的断裂构造对马扎拉锑金矿起着重要的控矿作用。
综上所述,运用分形理论对断裂构造进行分析,可以对研究区内断裂构造的分布情况、发育程度、复杂程度进行定量的科学的描述,更能为成矿远景区评价提供有力的依据[1]。
2研究区断裂构造分形特征及分维值
2.1断裂特征
大量科研成果和生产实践表明,研究区是我国重要的金矿矿集区,区内断裂构造发育,如图1所示(据招远市地质矿产局,1998)。

图1 1/5 000万招远地区断裂构造与金矿分布图
从图1可看出研究区主要发育有NNE(5°~30°)、NE(30°~60°)、近EW(85°~95°)、NW(300°~330°)向断裂(下同)。其中以NNE向断裂为主,其中NNE向断裂多经历了晚侏罗世—早白垩世早期的走滑,早白垩世—古近纪的伸展和新近纪以来的挤压逆冲的演化过程[23-24],在伸展时期控制了该区矿产的形成与分布,规模较大者为招平和焦家2个主断裂带,它们既构成重要矿集区的边界,也构成良好的储矿空间,它们直接控制了本地区特大型、大型金矿床及大部分中小型金矿床。
90%以上的大、中型金矿均位于焦家断裂的SE侧及招平断裂的NW侧,即均位于控矿断裂带的下盘。
2.2分维值的计算与结果分析
在断裂研究上,一般用Hausdorff维数来确定断裂的分维值,为容量维数的发展,是以覆盖为基础的。若应用到断裂分维值的计算,具体做法是数盒子法,即盒维数法。以边长为r的正方形格子构成的二维正交网格去覆盖研究区,计算覆盖到断层的网格数N(r),再不断变换r,分别求出N(r),若N(r)与r满足幂定律关系,即(1)式,则研究对象为分形。
(1)
其中,C、D为常数。将(1)式两边分别取对数得:
lgN(r)=-Dlgr+lgC
(2)
由(2)式可知,若lgN(r)与lgr为线性关系,则研究对象为分形,分维值D即为该线性关系式的绝对值。
为了以分形理论来证明招远金矿区断裂对矿床的控制,本文采用盒维数法测定研究区断裂构造的分维值D,具体做法为:用边长为r正方形格网覆盖研究区,统计被断裂穿插的网格数N(r),通过不断变换r的大小得到N(r)与r的关系表。正方形格网的生成可利用ArcGIS中的“创建鱼网”功能完成,把生成的格网面要素与断裂线要素做相交分析,会生成新的线要素,在其属性表中即可统计出被断裂穿插的格网数量N(r),最终获得的统计结果见表1所列。在Grapher中对lgr和lgN(r)做一元线性回归分析,结果如图2所示,从图2可以看出,招远金矿区各个方向上断裂构造的lgr与lgN(r)之间呈明显的线性关系,研究区断裂构造在1~5 km标度区间内具有良好的分形分维特征,分维值为1.48。

表1 招远地区断裂构造分维值计算统计结果

图2 招远地区断裂构造分维值计算双对数图
文献[19]认为,地质体的连通性与断裂构造的分维值有关,当分维值低于某个临界值时,地质体连通性较差,高于临界值时,地质体的连通性较高。而文献[25]通过对岩石块体做二轴压缩试验的数值模拟得出这个临界值为1.22~1.38。通过上述计算得出招远地区断裂构造的分维值为1.48,大于临界值,表明招远地区地质体具有很好的连通性,断裂构造的发育为成矿流体的运移、汇聚提供了有利的通道和场所,对金矿床的形成具有控制作用。
招远地区主要发育有NNE向、NE向、近EW向、NW向4组断裂构造,每组断裂的发育程度、复杂程度各不相同。分别对4组断裂构造做分形分析,结果见表2所列,如图3所示,NNE向、NE向、近EW向、NW向4组断裂构造分维值分别为1.223、1.194、0.864、0.781。
可以看出,招远矿集区单独每个方向的断裂构造分维值都没有达到临界值(1.22~1.38),所以单个方向断裂构造是难以成矿的,金矿的形成是各个方向断裂综合作用的结果。
由分析结果可以看出:
NNE向断裂构造最复杂,分维值也最大,为招远地区主导性构造,其强度大于其他方向的断裂构造,对金矿床形成的贡献也最大;其次为NE向断裂构造,复杂度仅次于NNE向断裂,亦是重要的导矿、容矿构造。

表2 招远地区NNE、NE、EW、NW向断裂构造分维值计算统计结果
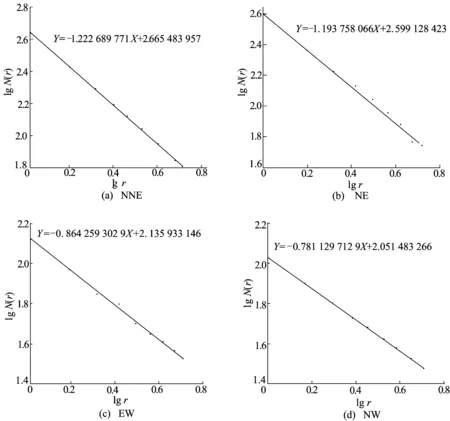
图3 招远地区NNE、NE、EW、NW向断裂构造分维值计算双对数图
3断裂分维值与金矿分布的关系
断裂组成越复杂,规模越大,断裂分布的分维值越高,断裂构造活动性越强,越有利于成矿流体的运移、聚集,从而有利于大型、超大型矿床的形成。而断裂分维值的大小,定量地描述了断裂构造的分布情况、发育程度及复杂程度,反映了研究区内断裂系统演化过程中时空上的非均质性以及断裂系统分形几何形态上的差异,从而直接影响区内金矿床的分布情况。招远地区NNE向断裂构造分维值最高(1.223),其次为NE向断裂构造分维值(1.194),EW向断裂构造分维值(0.864)及NW向断裂构造分维值(0.781)最小。从招远金矿区内断裂分维值来看,NNE向构造活动强度最大。
从图1可看出,区内金矿床90%均分布于招平与焦家断裂带及其所夹区域。区内金矿床主要沿NNE向断裂分布,主要分布于招平与焦家两大NNE向主断裂带上,少数沿NE向断裂分布,极少数沿EW、NW向断裂分布,而NNE向断裂分维值明显大于NE、EW及NW向断裂分维值。从金矿规模来看,大型、超大型金矿床均沿断裂带分布,而中小型金矿床分布于NNE、NE向断裂及断裂交汇部位,极少数分布于EW、NW向断裂。以上结果表明了研究区内断裂体系断裂构造分维值越大,越有利于金矿床的分布,构造活动强度较大的区域有利于成矿物质的流通与聚集,断裂构造对金矿床的分布起控制作用。
4结论
(1) 招远金矿矿集区断裂体系的分布具有良好的分形特征,区内断裂构造的分维值为1.48,大于地质体连通性临界值(1.22~1.38),表明招远地区地质体具有很好的连通性,断裂构造的发育为成矿流体的运移、汇聚提供了有利的通道和场所,对金矿床的形成具有控制作用。但单独每个方向断裂构造(NNE、NE、EW、NW向断裂)的分维值都没有达到临界值,因此单个方向断裂构造是难以成矿的,招远金矿床的形成是各个方向断裂综合作用的结果。
(2) 断裂分维计算表明,区内以NNE、NE向断裂较高,反映出NNE、NE向断裂系统复杂程度较高,而且也反映出该方位断裂对矿产的控制强度大,这与区内大型超大型金矿床多沿着NNE向断裂分布,尤其是招平、焦家断裂带,NNE向断裂起导矿、控矿作用这一地质事实相吻合。上述结果说明了NNE—NE向断裂拐点及其与不同方位断裂交叉处为本区有利控矿部位。
(3) 断裂体系平面分布的分维值越大,则断裂组成越复杂,规模越大,断裂构造活动性越强,越有利于金矿床的分布,金矿规模越大。分形理论可以被用于研究断裂构造与金矿床的空间分布关系,这为断裂构造对固体矿产分布的控制作用提供了新思路及定量化研究方法。
[参考文献]
[1]徐建华.现代地理学中的数学方法[M].北京:高等教育出版社,2002:392-416.
[2]曾文曲.分形理论与分形的计算机模拟[M].沈阳:东北大学出版社,1993:1-22.
[3]Mandelbrot B B. Fractal geometry of nature[M].New York:W H Freeman and Company,1983:1-24.
[4]Feder J. Fractals[M].New York:Plenum Press,1988:1-284.
[5]张飞燕,陈晓山.分形概念及其在构造地质研究中的应用[J].中国煤炭地质,2008,20(3):16-19.
[6]黄丹,廖太平,邓吉州,等.分形理论在断裂构造研究中的应用前景[J].重庆科技学院学报:自然科学版,2010,12(6):83-85.
[7]苗来成,罗镇宽,关康.胶东招掖成矿带控矿断裂演化规律[J].地质找矿论丛,1997,12(1):26-34.
[8]苗来成,翟裕生,朱成伟.花岗岩类侵入体与金矿化关系探讨:以胶东招掖成矿带为例[J].地球学报,1999,20:332-336.
[9]汪劲草,王国富,汤静如.玲珑—焦家地区金矿成矿构造体制的新认识[J].桂林工学院学报,2002,22(1):1-3.
[10]邓军,翟裕生,杨立强,等.构造演化与成矿系统动力学:以胶东金矿集中区为例[J].地学前缘,1999,6(2):315-323.
[11]邓军,王庆飞,杨立强,等.胶西北金矿集区成矿作用发生的地质背景[J].地学前缘,2004,11(4):527-533.
[12]刘日富.胶东西北地区金矿床控矿构造特征及金矿床类型[J].黄金,1997,18(7):13-15.
[13]赵财胜,匡俊,李碧乐,等.山东招远大河金矿断裂构造控矿规律及成矿预测[J].黄金,2003,24(17):17-20.
[14]蔡新平.试论郯庐断裂带对胶东金矿集中区形成的巨大作用[J].山东地质,1993,9(2): 93-101.
[15]杜松金,李洪喜,张庆龙,等.山东招远玲珑金矿田控矿构造及其形成机制[J].高校地质学报,2003,9(3):420-426.
[16]刘志刚.玲珑金矿田控矿构造研究[J].长春地质学院学报,1983(3):47-54.
[17]于昆,刘国生,陈皓龙,等.夏甸金矿床主、微量元素特征及其地质意义[J].中国有色金属学报,2014,24(10):2621-2633.
[18]周庆卫.郯庐断裂带对招远地区金矿控制规律研究及其意义[D].合肥:合肥工业大学,2014.
[19]谢焱石,谭凯旋.断裂构造的分形研究及其地质应用[J].地质地球化学,2002,30(1): 71-77.
[20]曾联波,金之钧,李京昌,等.柴达木盆地北缘断裂构造分形特征与油气分布关系研究[J].地质科学,2001,36(2): 241-247.
[21]韩喜彬,梁金城,冯佐海,等.桂东南地区断裂构造分形特征与金银成矿关系研究[J].广西科学,2003,10(2):117-121.
[22]董富权.西藏古堆—隆子地区断裂构造分形特征及其地质意义[J].黄金科学技术,2012,20(6):41-45.
[23]陈皓龙.郯庐及其旁侧地块(招远、蚌埠)断裂构造特征与演化[D].合肥:合肥工业大学,2014.
[24]陈皓龙,刘国生.郯庐断裂带(五河段)演化特征与矿化关系研究[J].合肥工业大学学报:自然科学版,2014,37(11):1353-1360.
[25]Zhang X, Sanderson D J. Fractal structure and deformation of fractured rock masses[M]//Kruhl S H. Fractals and Dynamics Systems in Geoscience.New York: Spring-Verlag,1994:37-52.
(责任编辑张淑艳)
Application of fractal theory in the study of the relationship between fracture and mineral
LI Fei,LIU Guo-sheng,ZHOU Qing-wei,ZHAO Guang-bao
(School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract:Taking Zhaoyuan gold ore district as an example, and based on a field survey of the relationship between fracture and mineral distribution in the studied area, a fractal research on the faults system in the area was conducted by using the box-counting method of fractal theory, and the relationship between fracture and mineral distribution and the occurrence regularity of mineral were summarized. Through the calculation of fractal, the overall fractal dimension D value of Zhaoyuan faults structure is 1.48, the critical value of fracture fractal dimension of geological connectivity is 1.22-1.38. Fractal dimensions corresponding to different fractures are as follows: in the NNE,D is 1.223; in the NE,D is 1.194; in the direction close to EW,D is 0.864;in the NW, D is 0.781. The results show that the complexity of NNE and NE trending fracture systems is higher, and this orientation of the fracture controls the mineral to a higher degree. This coincides with the geological fact that large and ultra-large gold deposits in the area mostly distribute along the NNE trending faults, especially Zhaoping and Jiaojia faults, due to the ore leading and controlling effect of NNE trending faults. It is also shown that the existence and development degree of the inflection points of NNE and NE trending faults and their intersections with the fractures in different directions affect the distribution of gold deposits.
Key words:fractal theory; fractal dimension; ore-controlling fault; gold mine; Zhaoyuan
收稿日期:2015-01-30;修回日期:2015-03-26
基金项目:国家自然科学基金资助项目(41172187);中国地质调查局资助项目(1212011121096)
作者简介:李飞(1993-),男,安徽六安人,合肥工业大学硕士生; 刘国生(1957-),男,河北邢台人,博士,合肥工业大学教授,硕士生导师.
doi:10.3969/j.issn.1003-5060.2016.05.024
中图分类号:P612
文献标识码:A
文章编号:1003-5060(2016)05-0701-06

