环q+uFq+u2Fq+…+uk-1Fq上线性码关于齐次度量的完备性

陈晓玲,　李　平

(合肥工业大学 数学学院,安徽 合肥　230009)

环q+uFq+u2Fq+…+uk-1Fq上线性码关于齐次度量的完备性

陈晓玲,李平

(合肥工业大学 数学学院,安徽 合肥230009)

摘要:文章约定R=Fq+uFq+u2Fq+…+uk-1Fq,其中uk=0,q为某一素数幂,研究环R上的线性码关于齐次度量的完备性,得到了环R上的线性码的球形填充界,并且利用这些界去检验线性码的完备性,讨论了环R上2种特殊情况下关于齐次度量的完备线性码的存在性。

关键词:齐次距离;齐次重量;完备码

0引言

线性码的完备性是编码理论的重要问题之一,20世纪70年代已确定了有限域中的完备码的参数[1-2]。近年来,有限链环上的线性码引起编码爱好者的极大兴趣。文献[3]给出了一些高效的二元码,将其看成环Z4上线性码的Gray像,并将Lee重量引入环Z4。文献[4]首次将齐次距离的概念引入整数剩余类环中。整数剩余类环上的齐次距离是有限域上Hamming重量和剩余类环Z4上Lee重量的推广,有着许多重要的应用[5],从而引起人们关注整数剩余类环上关于齐次距离的完备码的研究。文献[6]研究了Z4上的线性码关于齐次距离的完备码的存在性,文献[7]将文献[6]的结果推广到环Z2l上。至此,环Z4和环Z2l上关于齐次距离的完备码的存在性问题已经部分解决。多项式剩余类环R=Fq+uFq+u2Fq+…+uk-1Fq上线性码由于具有良好性质被广泛研究[8-11],得到环R上线性码齐次距离的许多界[10-11],但关于其上的线性码的完备性的讨论却很少。本文研究环R上关于齐次度量的完备码的存在性,利用计算球内的码字的个数的方法,找到环R上线性码的完备性的条件,说明了2种特殊情况下线性码是不完备的。

1预备知识

设R=Fq+uFq+u2Fq+…+uk-1Fq,其中uk=0,Fq是q元域,q为某素数的方幂。环R是以〈u〉为极大理想的有限链环。对任意的r∈R,都可以唯一表示为:

其中ri∈Fq,0≤i≤k-1。

环R上长为n码C是Rn的一个非空子集,当C是Rn的R-子模时,则称C为一个线性码。当线性码C有ql个码字时,称C为[n,l]码。下面给出环R上齐次重量函数的定义。

定义1环R上的齐次重量Wth(x)定义为:

定义2对于任意的u,v∈C,2个码字的齐次距离dh(u,v)为:

设C是一个线性码,码C的齐次距离(也是齐次重量)d(C)定义为C中非零码字的齐次重量的最小值,即

为了更好地分析环R上线性码的性质。下面,给出环R上线性码的结构[9]。

引理1有限链环R上的任意线性码C的生成矩阵经过置换可以写成下面的形式:

其中,Ikj为ki阶单位矩阵;ti为正整数,0≤t≤k,并且t0+t1+…+tk-1=n;Aij为定义在Fq上的矩阵。称C为{t0,t1,…,tk-1}型的线性码。

2环R上线性码的完备性

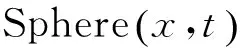
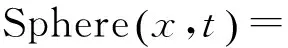
定义3对于任意的x,y∈C, 当x≠y时,若线性码C满足:

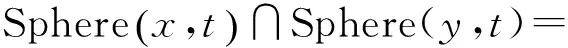
(1)

称码C是一个t-纠错码,若进一步满足:

(2)

则称码C是一个t-完备线性码。

(3)

定理2设C是一个有ql个码字的t-纠错码,则有:

(4)

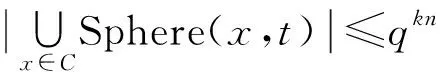
定理2中的(4)式称为码C的球形填充界。结合定义3和定理1,不难得到,一个t-纠错的[n,l]码C是完备码当且仅当定理2中的(4)式取等号。当t取定之后,(4)式的值取决于不等式组(5)式的解。

(5)

记(5)式的解集为:

下面给出t取部分具体值时的球形填充界,然后利用这些界去检验完备线性码的存在性。

推论1设C是环R上的一个t-纠错的[n,l]码,则

1）符合喘证诊断标准，目前处于稳定期；2）年龄在30～80岁之间，性别不限；3）患者知情同意，可按研究要求坚持检查和治疗及随访。

(1) 当t=(q-1)qk-2时,有

(2) 当t=qk-1,q≠2时,有

当q=2时,有

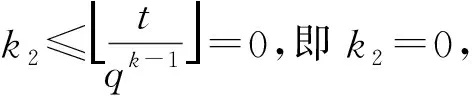
所以有1+n(qk-1)≤qkn-l。

当q=2时,则(5)式的解集为St={(0,0),(1,0),(0,1),(2,0)},代入定理2中的(4)式得:

化简得:

为给出推论1中的齐次重量t-纠错完备码的存在性,先给出引理2。

引理2设n、k为某正整数,存在正整数m使得n=2m-1,l=n-m,当且仅当k=1,关于l的方程(6)式有正整数解。

(6)

证明当k=1时,(6)式变为n+1=2n-l,易证n+1=2n-l,从中推出l=n-lb(n+1),所以(6)式有正整数解当且仅当存在正整数m，使得n=2m-1,l=n-m。

下面证明当k≥2时,(6)式无整数解。

假设(6)式有解l0,令m=kn-l0,移项得:

(7)

设a=(22k-1-2k+1+2)≠0,b=(-22k-1-3×2k-3),c=1-2m,所以可将(7)式看成一个关于n的一元二次方程,其判别式为:

易得Δ>0,所以方程有2个不相等的根,如果二次方程有一个正整数根为r1,如果另外一个根也是整数,则这个方程就有2个整数根,但由韦达定理知,两根之和为:

其中,t是正整数。又因为：

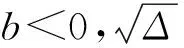
设x=2k,因此有:

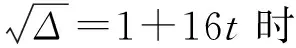
定理3环R上t-纠错的完备线性码是不存在的,其中,t=(q-1)qk-2或者t=qk-1。

证明由推论1,若存在(q-1)qk-2-纠错的完备线性码,则存在[n,l]码使得1+n(qk-q)=qkn-l成立,方程两边同时模q得1≡0(modq),这与q为素数的方幂矛盾,故不存在(q-1)qk-2-纠错的完备线性码。

当t=qk-1时,分2类讨论。第1类,q=2,由推论1得,若存在qk-1-纠错的完备线性码,则存在[n,l]码使得:

(8)

但引理2证明了(8)式有解当且仅当k=1且存在正整数m，使得n=2m-1,l=n-m。此时多项式剩余类环退化为二元域F2,且二元汉明码恰好是1-纠错完备码。当k≥2时,均不存在完备码。

第2类,q≠2,由推论1得,若存在qk-1-纠错的完备线性码,则存在[n,l]码使得1+n(qk-1)=qkn-l，方程两边同时模q得n≡1(modq),所以,可设n=qmb+1,(b,q)=1,代回原方程化简得:

(9)

(1) 当k≤m时,(9)式右边提出qk因子得:

因为 [(qm-qm-k)b+1]与q互素,且qkqmb+k-l是q的方幂,因此有:

又因为qm≥qm-k,所以有:

矛盾。

(2) 当k>m时,(9)式右边提出qm因子得:

(9)式成立当且仅当:

也就是满足(qk-1)b=1-qk-m,由此推出1-qk-m≥0,qk-m≤1,即k=m,矛盾。

故此t-完备线性码是不存在的。

证毕。

3结束语

本文介绍了环R上线性码的性质和结构,研究了环R上的关于齐次度量的完备线性码的存在性问题,证明出了环R上2种特殊情况下完备线性码是不存在的,推广了文献[7]的结果。

[参考文献]

[1]Tietavainen A. On the nonexistence of perfect codes over finite fields[J].SIAM Journal on Applied Mathematics,1973,24(1):88-96.

[2]MacWilliams F J,Sloane N J A.The theory of error correcting codes[M].Amsterdam:North-Holland Pub Co,1997:32-54.

[3]Hammons A R,Jr,Kumar P V,Calderbank A R,et al.TheZ4-linearity of Kerdock,Preparata, Goethals, and related codes[J]. IEEE Transaction on Information Theory,1994,40(2):301-319.

[4]Constantinescu I, Heise W. A metric for codes over residue class rings of integers [J].Problemy Peredachi Informatii, 1997,33(3):22-28.

[5]Greferath M, Schmidt S E. Finite-ring combinatorics and MacWilliams’ equivalence theorem [J]. J Combin Theory, Ser A, 2000,92(1):17-28.

[6]Ozen M, Siap V. On the existence of perfect linear codes overZ4with respect to homogenous weight[J]. Applied Mathematicaal Sciences,2012,6(41):2005-2011.

[7]Siap I,Ozen M,SiapV.On the existence of perfect linear codes overZ2lwith respect to homogenous metric[J].Arabain Journal for Science and Engineering, 2013,38(8):2189-2192.

[8]李平,朱士信.论环FP+uFP+…uk-1FP上的循环码 [J].合肥工业大学学报:自然科学版, 2006,29 (6):794-797.

[9]朱士信,李岩,邓林.环Fq+uFq+u2Fq+…+uk-1Fq上的一类常循环码 MDS码[J].中国科学技术大学学报,2013,43(3):494-497.

[10]刘晓娟,朱士信.环FPm+uFPm+u2FPm+…+uk-1FPm上的长为Ps的(1+λu)常循环码的距离分布[J]. 中国科学技术大学学报,2012,42(11):931-935.

[11]朱士信,黄素娟.环FPm+uFPm+u2FPm+…+uk-1FPm上(1+u)常循环码的距离分布[J]. 电子与信息学报,2013,35(11):931-935.

(责任编辑张淑艳)

On the existence of perfect linear codes overFq+uFq+u2Fq+…+uk-1Fqwith respect to homogeneous metric

CHEN Xiao-ling,LI Ping

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

Abstract:In this paper, R denotes the ring Fq+uFq+u2Fq+…+uk-1Fq, where uk=0 and q is a power of a prime. The existence of perfect linear codes over Fq+uFq+u2Fq+…+uk-1Fq with respect to homogeneous metric is studied, and the sphere bounds of linear codes over R are obtained. The existence of perfect linear codes over R with respect to homogeneous metric under two kinds of special circumstances is discussed by using the bounds.

Key words:homogeneous distance; homogeneous weight; perfect code

收稿日期：2015-02-09

基金项目：国家自然科学基金资助项目(61370089)

作者简介：陈晓玲(1991-),女,安徽合肥人,合肥工业大学硕士生;

doi:10.3969/j.issn.1003-5060.2016.05.026

中图分类号:TN911.22

文献标识码：A

文章编号：1003-5060(2016)05-0712-04

李平(1971-),男,安徽无为人,博士,合肥工业大学副教授,硕士生导师.