地震作用下贮液结构象足位置样条插值分析方法

胡明祎 ,　张令心,　娄　宇 ,　陈　骝 ,　黄　伟

(1.中国电子工程设计院, 北京　100142; 2.北京市微振动环境控制工程技术研究中心, 北京　100086; 3.清华大学 土木水利工程学院,北京　100084; 4.中国地震局工程力学研究所,黑龙江 哈尔滨　150080; 5.合肥工业大学 土木与水利工程学院,安徽 合肥　230009; 6.土木工程结构与材料安徽省重点实验室,安徽 合肥　230009)

地震作用下贮液结构象足位置样条插值分析方法

胡明祎1,2,3,张令心1,4,娄宇1,2,陈骝1,2,黄伟5,6

(1.中国电子工程设计院, 北京100142; 2.北京市微振动环境控制工程技术研究中心, 北京100086; 3.清华大学 土木水利工程学院,北京100084; 4.中国地震局工程力学研究所,黑龙江 哈尔滨150080; 5.合肥工业大学 土木与水利工程学院,安徽 合肥230009; 6.土木工程结构与材料安徽省重点实验室,安徽 合肥230009)

摘要:贮液结构的象足式破坏是一种典型的震害现象,为了有效地减轻或避免象足式震害,文章采用有限元方法(FEM)和数学插值方法对地震中贮液结构产生象足破坏的位置进行了研究。首先将数值计算结果进行指数公式拟合,确定出快速判断象足破坏位置的方法,然后对象足部位进行合理的结构优化设计以提高贮液结构抗震性能。在分析过程中,利用FEM方法对贮液结构地震响应进行数值模拟,考虑了液固耦合效应,同时根据已知结构响应在某一区域收敛于某个极值的条件,采用样条插值方法确定象足产生的位置,提出在有限计算资源情况下,利用样条函数插值分析低精度FEM数值计算结果以获取高精度结构响应的方法,并通过实例验证了该方法的实用性。

关键词:贮液结构;地震响应;有限元方法;插值

贮液结构的地震破坏一般包括如下3种形式:① 倾覆弯矩过大引起结构整体倾覆; ② 基底剪力过大引起结构底部开裂、材料失效; ③环向力和轴向力共同作用引起结构下部材料屈曲,亦称象足屈曲。本文主要针对象足屈曲震害现象进行贮液结构地震响应优化应用方法研究。研究内容是在有限计算资源条件下,寻求一种简易计算方法,可以快速确定象足位置,据此对结构进行优化设计以提高贮液结构抵抗象足屈曲的能力。

利用FEM进行数值计算时,保证有限元计算精度的常用措施是增加网格划分密度,但在计算资源有限的情况下,特别是对于考虑液固耦合状态非线性的贮液结构地震反应问题,增加网格密度会因计算机运算能力所限而降低求解效率。但是,如果在低密度网格情况下,已经准确获悉结构响应在某一区域内收敛于极大值或极小值,那么通过适当地提高网格划分密度,采用数学插值的手段对该区域响应值进行高精度插值,便可以有效地提高结构有限元计算精度。因此,本文的技术问题便归结于利用数学插值方法对一定精度条件下的有限元计算结果进行插值分析,从而获取高精度结构响应结果。

1贮液结构FEM数值模拟

贮液结构有限元数值模拟工作已经开展多年,目前有多种数值简化计算模型。文献[1]在前人研究的基础上提出了质量弹簧系统的储液罐刚性简化模型;文献[2]深入研究了贮液结构弹性变形对液固耦合效应影响的重要性,推广应用液固耦合半解析半数值计算模型;文献[3]利用有限元方法研究液固耦合振动问题;文献[4] 提出关于弹性圆柱形储液罐地震反应解析解分析模型;文献[5]采用附加质量模型,建立了液固耦合边界处的附加质量矩阵以确保液固耦合方程有解条件的连续性;文献[6]采用Sanders壳体有限元理论将液固耦合振动方程按线性降阶处理建立了FEM模型;文献[7]提出了考虑弹性变形的柔性罐壁单自由度质点模型;文献[8]提出了Haroun-Housner三分量模型。总之,在材料模型可靠的条件下,FEM模型要比解析解模型能更加真实地模拟贮液结构振动问题,随着有限元理论的飞速发展,FEM模型在贮液结构地震响应研究中也得到了很好的应用[9-10]。

贮液结构地震响应数值模拟的难点包括结构材料理论属性、液固耦合相互作用、结构弹性变形对计算结果产生的影响等。本文采用FEM方法建立贮液结构数值模型时,假设贮液振动为小幅振动,贮液为无旋无黏性流体,有限元模型中,贮液结构采用shell单元,具有6个自由度,材料为双线性弹塑性模型,贮液采用势流体单元,具有3个平动自由度。贮液结构有限元模型剖面图如图1a所示,采用的地震荷载为ELcentro地震动,加速度峰值为341 cm/s2,加载时间为20 s,步长取为0.02 s。图1b所示为贮液结构地震响应象足效应图。

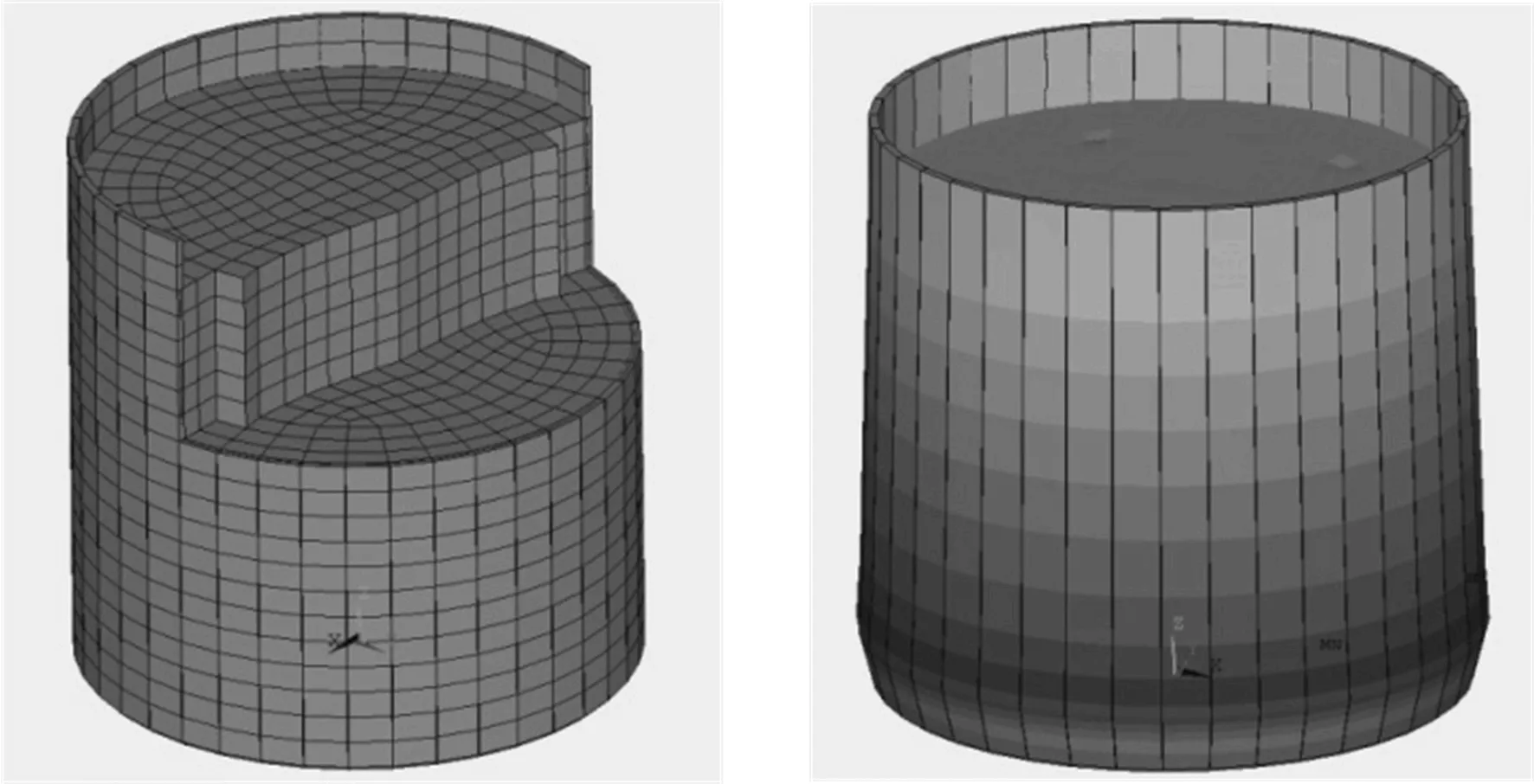
(a)　有限元模型剖面图　　(b)　地震响应象足效应图

2样条函数插值分析

样条函数插值已经被广泛地应用到流线型形状设计问题中,其应用的目标状态是保证有限插值控制的精确性和收敛性。相对Lagrange插值函数和三次Hermite插值而言,样条函数插值优势是既能有效地避免产生边界Runge现象,也能成功解决平滑化问题。样条插值的函数基为三次多项式函数,而且其一阶、二阶导数在插值控制点都是连续的。

假设F″(xj)=Mj,j=1,2,3,…,n,由于F(x)是二阶光滑的分段三次多项式,于是F″(x)是分段线性连续函数,可以在x∈[xj,xj+1]上假设F″(x)函数形式为:

(1)

其中,x∈[xj,xj+1]。对(1)式进行两次积分可得:

(2)

建立插值条件(3)式、(4)式,可以求解出系数Aj和Bj,即

(3)

(4)

(5)

(6)

假设插值函数一阶导数连续,F′(xj+0)=F′(xj-0),同时采用第2类边界条件F″(a)=F″(b)=0,联立可以建立如下线性方程组:

(7)

其中,λj=(xj+1-xj)/(xj+1-xj-1);μj=1-λj;f[xj-1xjxj+1]为点xj-1、xj、xj+1的二阶差商。求解(7)式进而可以得到Mj值,返回带入(5)式、(6)式可以求解系数Aj和Bj,再带入(2)式最后进行插值求解。

需要注意的是插值求解过程中,也可以根据情况调整边界条件,但是通过多次调试对比,笔者认为文中给出插值边界条件较为稳定,与精细网格有限元模型计算结果相比象足位置计算结果误差低于10-5,因此本文的边界条件采用第2类边界条件,具体取值规定为二阶导数为零。

从理论角度而言,如果所有插值区域具有同样的属性,并且严格在插值点具有收敛特征,那么样条函数插值是一种很好的数值逼近方法。本文中,假设研究的对象材料分布连续并且均匀,其地震响应沿结构壁高度分布也具有连续并且收敛的特征,因此可以采用样条函数插值方法对结构最大响应位置进行插值逼近求解。

图2所示为基于FEM计算结果的插值分析程序流程图。

图2　基于FEM计算结果的插值分析程序流程图

根据上述方法,按照图2中的流程图编制插值分析程序,可以结合贮液结构地震反应FEM数值计算结果进行插值分析。分析之前要确定插值分析的数据使用条件,即保证插值控制点的有效性。通过前面FEM数值模拟,本文选用的模型网格划分密度为0.05 m,所以结构壁最大反应及象足高度位置的计算精度也为0.05 m。为了说明该精度对于插值控制点的有效性,通过细化网格密度范围为0.05～0.001 m,重新计算分析,可以证实网格密度为0.05 m和低于0.05 m的结构响应结果误差基本在1.5%以内,表1所列为不同网格密度对应象足位置计算精度比较,如果按照允许误差1%考虑,在0.05 m的网格划分密度条件下,FEM数值计算结果针对于象足高度位置的精度可以达到0.01 m,这种结果同时也表明按0.05 m的网格密度计算出的象足位置可以保证插值控制点的有效性。

表1　不同网格密度对应象足位置计算精度比较

注:斜线后为贮液结构地震响应计算结果相对网格密度为0.05 m情况下的误差率;黑体为有效精度确定位置。

基于上述条件,对贮液结构的FEM计算结果进行插值分析。插值结果检验目标有2项,即插值结果稳定性和插值曲线平滑化。为了说明样条函数插值结果的优势,本文采用Lagrange高阶插值函数、分段Lagrange抛物线插值函数和三次样条插值函数对FEM计算结果进行插值结果对比,这里给出其中4种工况的计算分析结果,如图3所示。图3中D为贮液结构直径;H为贮液结构高度;Hw为贮液高度；φ为有效精度；A、B、C、D、E、F为插值控制点。由图3a、图3b可以清晰看到对于不同贮液量的细高贮液结构而言,Lagrange高阶插值函数在边界处产生显著的Runge现象,引起边界处插值不稳定性,分段Lagrange抛物线插值会有效降低Runge现象程度,但是整体曲线平滑性较差,三次样条函数插值结果很好地避免了上述问题,并且有效地保证了精度水平为0.01 m。

图3c、图3d研究对象为相同贮液量不同高度的矮胖贮液结构,可以看到这种结构地震响应Lagrange高阶插值和三次样条插值结果基本一致,而且Runge现象不显著。此外,通过比较,样条函数插值最终的结果精度保证在0.01 m水平,图3中有效精度误差分别为0.14、0.11、0.08、0.13 m,最大相对精度误差是图3a，为28%,这意味着通过插值分析确定的象足位置高度值精度比FEM直接计算值提高28%。这种计算精度的有效提升对于象足位置的地震响应优化设计而言具有重要意义。

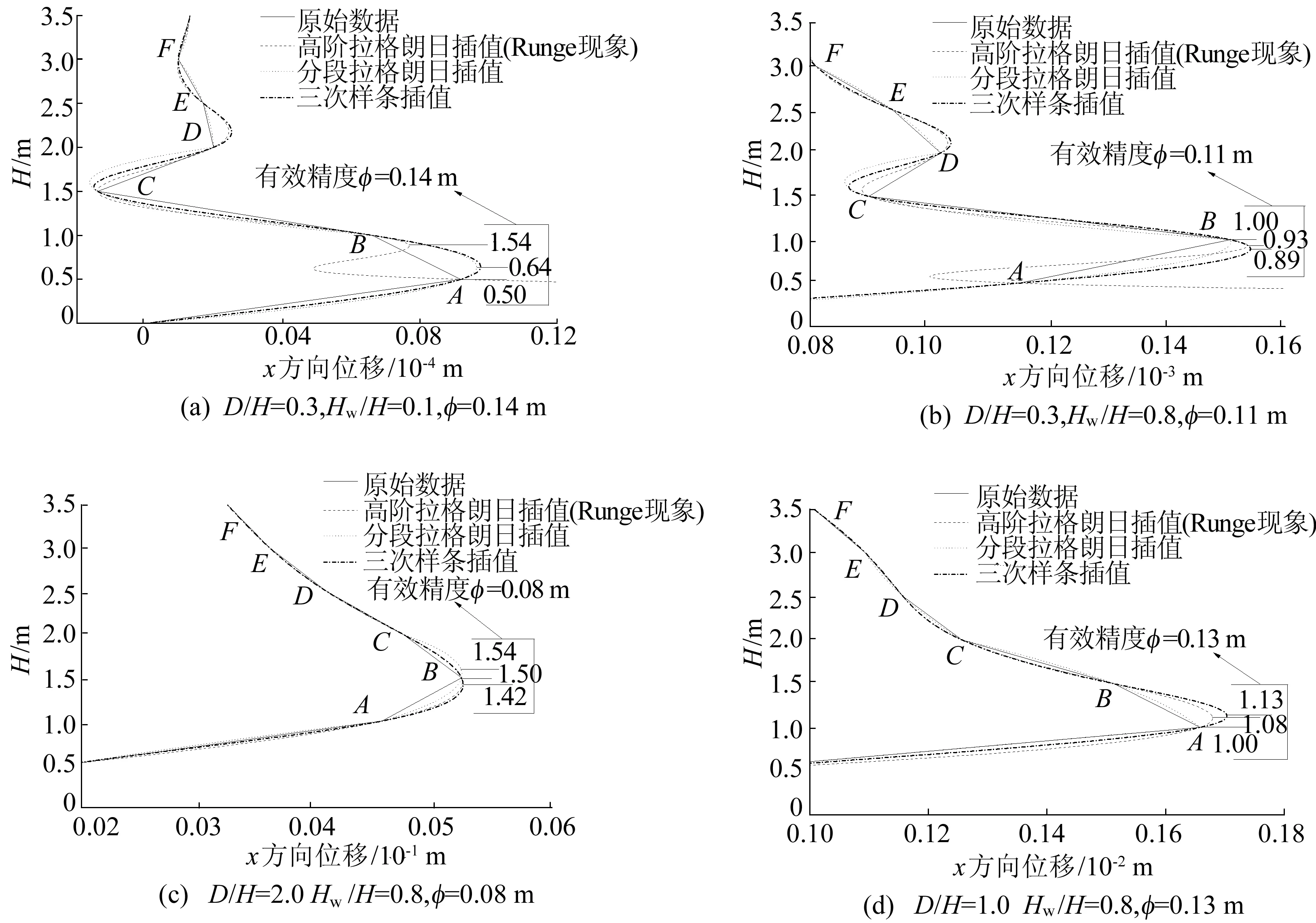
图3　插值比较曲线

3插值结果拟合分析

通过前面针对FEM数值计算结果的插值精度分析,可以确定样条函数插值获取的象足位置插值结果是有效的,下面对不同工况下的插值结果进行统计分析,确定象足位置与D/H值和Hw/H值的关系,从而为后面的优化工作提供依据。图4所示为D/H值取0.5和1.0对应的象足高度值Hmax随Hw/H的等效坐标值的变化曲线

通过图4,根据插值结果Hmax曲线指数衰减关系,可以进行指数函数拟合,图4a、图4b对应函数形式分别为(8)式、(9)式:

(8)

(9)

由图5可以发现随着D/H值和Hw/H不断增大,Hmax值也在增大,这个规律在贮液结构抗震设计中非常重要,通过这种插值拟合的方法将不同设计工况下的Hmax取值量化有利于实际应用。

采用这种方式,可以将Hmax值随D/H值和Hw/H值同时变化的曲线绘制在一起,可以得到图6所示的有水刚结顶盖Hmax随D/H变化曲线和有水浮顶盖Hmax随D/H变化曲线,两者的工况区别为贮液结构盖顶构筑形式不同。

图4　Hmax随Hw/H变化曲线

图5　Hmax随D/H变化曲线

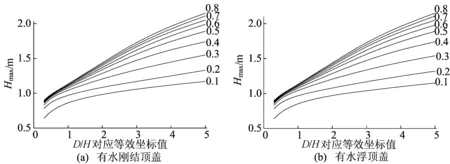
图6　Hw/H=0.9时Hmax随D/H变化曲线

由图6可以发现Hmax随D/H取值在贮液量较少时变化较小,贮液量较多时变化较大,也说明了液固耦合作用对结构的响应随贮液增加而变大,同时也发现盖顶形式对象足位置的高度影响不大。

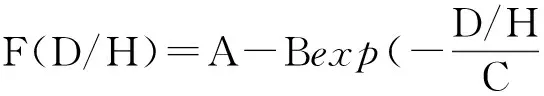
(10)

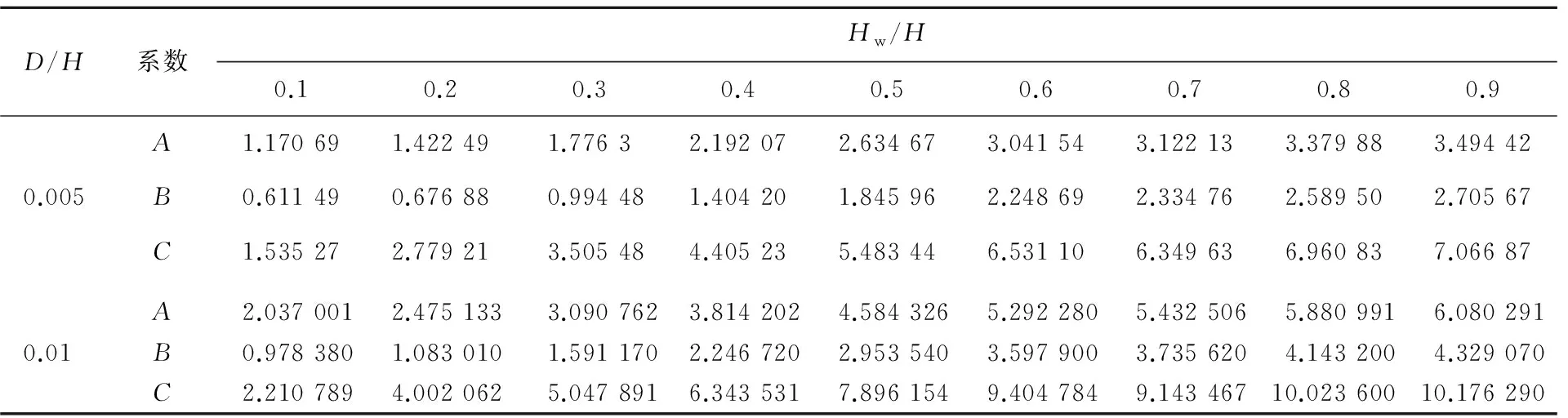
注:D/H值的范围为0.001～0.01,由于篇幅限制这里只给出部分值;实际应用中A、B、C值为拟合系数,可以按照表2进行线性插值取值。

4优化应用分析

根据上述基于对贮液结构地震反应FEM计算结果插值分析而拟合获取的象足位置计算公式及系数表格的确定方法,将该表格扩展到不同高度、厚度、形状或者其他影响因素,可以得到关于象足高度快速确定的设计参照系列表格,利用这些表格可以快速确定对应象足部位计算函数中的系数A、B、C值,从而获得不同抗震设计方案下的象足高度位置,进而对原结构形式进行优化设计。

具体的优化设计思路是在象足部位对贮液结构增加环形肋梁,通过这种实际的应用分析,可以快速对原设计方案进行抗震性能验算和确定对象足部位进行结构加固和功能补足。对于具体实例,图7a所示为FEM优化模型,图7b所示为优化后贮液结构地震响应象足效应图。在实际情况下,具体的设计方式也可以采用内部加环形肋梁,或者外部增加环向加劲肋,其增加的位置都是通过(10)式和设计参照表格得到的。

(a)　有限元模型剖面图　　　　　　(b)　地震响应示意图

图8所示为优化前和优化后的结构侧向最大位移随D/H变化的曲线对比图。

图8　优化设计前、后Hmax随D/H变化曲线

通过图8可以看出,优化后的FEM计算结果要明显小于优化前计算结果,其中对于Hw/H=0.8的工况下,结构最大侧向位移减小了40%。

5结论

本文针对考虑液固耦合相互作用的圆柱形贮液结构的象足破坏问题,在计算资源有限的情况下,利用FEM方法对贮液结构地震响应进行数值模拟,并利用样条插值手段对低精度FEM计算结果进行分析和比较,提出了利用样条函数插值分析低精度FEM数值计算结果获取高精度结构响应的方法,同时采用该方法计算结果,对贮液结构象足出现位置进行了指数公式拟合,从而对结构进行优化设计,改善其地震响应效果,最后对优化前后的贮液结构地震响应进行了对比,验证了该方法的实用性。具体结论如下:

(1) 在进行插值分析时,提出采用第2类插值边界条件F″(a)=F″(b)=0的方式进行,该边界条件可以很好地保证插值边界连续且平滑。

(2) 将FEM方法和插值方法相结合,编制了插值分析程序,通过确定FEM网格密度对贮液结构地震响应的影响,保证了FEM计算结果可用来进行插值分析的条件。

(3) 对象足部位确定公式,采用基于FEM和插值结果的指数衰减公式,绘制指数参数设计参照表格,这种方法可以应用于结构抗震验算中,并且地震响应优化效果较好。

虽然该方法可以在一定条件下有效地提高低精度FEM计算精度,但是在有限计算资源条件下,优化结构计算的精度划分区域,如局部采用FEM子结构或者局部进行插值分析的方法可以更好地提高FEM计算结果的精度,本文为此提供了有效的理论分析依据。

[参考文献]

[1]Housner G W. Dynamic pressures on accelerated fluid containers[J]. Bulletin of the SeismologicalSociety of America 1957,47:15-35.

[2]Veletsos A S. Seismic effects in flexible liquid storage tanks[C]//Proc 5th World Conference on Earthquake Engineering, Rome, Italy, Vol 1,1973:630-639.

[3]Edward N W.A procedure for dynamic analysis of thin walled cylindrical liquid storage tanks subjected to lateral ground motions[D]. Univ of Michigan, 1969.

[4]Tedesco J W, Kostem C N,Kalnins A. Free vibration analysis of cylindrical liquid storage tanks[J]. Comput Struct,1987,26 (6):957-964.

[5]Rajasankar J, Iyer N R, Appa R T V S R.A new 3-D finite element model to evaluate added mass for analysis of fluid structure interaction problems[J]. Int J Numer Methods Eng,1993, 36:997-1012.

[6]Nash W A. Response of liquid storage tanks to seismic motion[C]// Koiter W T,Mikhailov G K. Theory of Shells. North-Holland Publishing Company, 1980:393-403.

[7]Veletsos A S, Yang J Y. Earthquake response of liquid storage tanks[C]// Advances in Civil Engineering through Engineering Mechanics:Proceedings Annual EMD Specialty Conference ASCE, Raleigh, N C, USA,1977:1-24.

[8]Haroun M A, Housner G W. Seismic design of liquid storage tanks[J]. ASCE Journal of Technical Councils,1981,107 (1):191-207.

[9]Hu Mingyi,Zhang Lingxin,Liu Jieping,et al. Structural frequency topology optimization in seismic design based on FEM method[C]//The 14th WCEE,Beijing,China,2008:12-17.

[10]Hu Mingyi,Li Wei, Hou Yuxin.Numerical study on seismic response analysis of reinforced concrete aqueduct strucure[C]//International Symposium on Innovation & Sustainability of Structures in Civil Engineering,Shanghai, China,2007:28-30.

(责任编辑张镅)

Spline interpolation methods to confirm elephant-foot position of maximum deformation of liquid container during earthquake

HU Ming-yi1, 2, 3, ZHANG Ling-xin1, 4, LOU Yu1, 2, CHEN Liu1, 2, HUANG Wei5, 6

(1.China Electronics Engineering Design Institute, Beijing 100142, China; 2.Micro-vibration Environmental Control Engineering Technology Research Center of Beijing, Beijing 100086, China; 3.School of Civil Engineering, Tsinghua University, Beijing 100084, China; 4.Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China; 5.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China; 6.Anhui Key Laboratory of Structure and Materials in Civil Engineering, Hefei 230009, China)

Abstract:Damage of liquid container may be great due to elephant-foot-type buckling during earthquake in general. In this paper,the finite element method(FEM) and spline interpolation method are used to analyze the elephant-foot position of the container structure during earthquake.The numerical calculation results are fitted by exponential formula,and the method for rapidly evaluating the elephant-foot position is obtained.On this basis, the reasonable optimal design of the elephant-foot position is maded to improve the structure’s seismic behavior.In the whole analysis, the FEM is used to simulate the structure’s seismic response with consideration of fluid-structure interaction, and based on the finite element analysis result that the structure’s responses converge to an extreme value within certain region, the elephant-foot position is determined by spline interpolation method. Although the computing resource is limited, high precision structural response can be gotten by the presented method.The practicality of this method is validated by an example.

Key words:liquid container; seismic response; finite element method(FEM); interpolation

收稿日期：2015-08-03；修回日期：2015-09-30

基金项目：北京市科学技术委员会资助项目(Z131101002813083)

作者简介：胡明祎(1982-),男,河南固始人,博士,中国电子工程设计院高级工程师.

doi:10.3969/j.issn.1003-5060.2016.05.020

中图分类号:TU352

文献标识码：A

文章编号：1003-5060(2016)05-0677-07