带加强层的某超限高层结构优化分析

周　伟,　程长征

(合肥工业大学 土木与水利工程学院,安徽 合肥　230009)

带加强层的某超限高层结构优化分析

周伟,程长征

(合肥工业大学 土木与水利工程学院,安徽 合肥230009)

摘要:某超限高层项目总高度164.0 m,地上49层,采用混凝土框架-核心筒结构。文章针对核心筒Y向高宽比略大的特点,运用分析程序Midas Building建立有限元模型并布置了4种不同数量的加强层以分析其作用效果;主要进行了4种方案结构模型的自由振动、多遇地震下的反应谱以及罕遇地震下的动力弹塑性时程分析,所得结果可为同类工程提供参考。

关键词:框架-核心筒;超限高层;加强层;反应谱法;动力弹塑性

近年来,超限建筑在我国发展十分迅速[1]。随着结构复杂程度和高度的不断增加,控制结构在水平地震作用下的侧向位移显得愈加重要。通常利用避难层或者设备层布置几道加强层[2]有助于增强核心筒和外框架柱的协同作用,可以起到抗侧力优化的效果。加强层是用来连接外围框架和内部核心筒的水平伸臂结构层,如有必要也可在周边布置环带构件。

尽管加强层是一种有效减小结构侧移的措施,但在地震作用下易造成位移和内力的突变[3],形成薄弱层,给抗震设计带来隐患,故有必要对其进行详细分析。

1工程概况与结构超限情况

本工程为某酒店式公寓超限高层项目,结构总高度164.0 m,地上49层(第16、32层为避难层),地下2层。其中第1、2层为商用,层高分别为5.1、3.9 m,第3～47层为标准层,层高3.2 m(避难层层高3.9 m),第48、49层层高分别为5.75、3.85 m。主楼采用混凝土框架(局部型钢柱)-核心筒结构体系。外轮廓平面尺寸为41.4 m×34.4 m,长宽比为1.2,高宽比为4.8。核心筒尺寸为19.2 m×11.9 m,X向高宽比为8.5,Y向高宽比为13.8。根据文献[4]第3.3.1条钢筋混凝土高层建筑的最大适用高度,布置加强层后的结构属于B级高度的复杂超限高层结构。

该建筑设计使用年限50 a,安全等级为二级;结构抗震设防类别为丙类,抗震设防烈度为7度,基本地震加速度值为0.10g,建筑场地类别为Ⅱ类(设计地震分组为第1组,特征周期0.35 s),周期折减系数取0.85,阻尼比取0.05。根据场地安全性评价报告提供的参数,将多遇地震水平地震影响系数最大值调整为0.092。

2有限元计算模型

考虑到核心筒Y向高宽比略微不满足文献[4]不宜大于12的要求,仅靠框架柱和核心筒难以满足结构Y向刚度的需求,故引入加强层对结构体系进行抗侧力优化。考虑到有限刚度[5-6]的原则,加强层采用钢筋混凝土斜腹杆桁架的布置方式,混凝土材料等级为C35。

本文共讨论了4种不同的方案:方案1(无加强层)、方案2(第24层布置加强层)、方案3(第16、32层布置加强层)以及方案4(第12、24、36层布置加强层)。

布置加强层后,整体结构包含3道抗侧力体系:① 钢筋混凝土核心筒;② 混凝土和型钢混凝土框架柱;③ 钢筋混凝土伸臂和环带桁架。方案4的整体结构模型及加强层布置如图1所示。

不考虑地面以下部分,以负一层地下室顶板作为结构嵌固层,底部柱、核心筒剪力墙与嵌固层固接。楼板与墙采用壳单元模拟,梁、柱均采用空间梁单元模拟,加强层构件采用杆单元模拟。

图1　方案4整体结构模型及加强层布置示意图

3抗侧力优化体系的自由振动分析

Midas/Building就特征值问题提供了兰佐斯法和子空间迭代法。当几个频率接近时,子空间迭代法可以有效克服收敛速度慢的困难[7]。本文选用子空间迭代法,分别对4个算例进行特征值分析,考虑36个振型,其中前9阶自振周期Ti(i=1,2,…,9)见表1所列。

表1　4种方案不同结构模型前9阶自振周期计算结果　s

计算结果表明,各方案模型的振动形态相同,第1、2阶振型为平面内平动,第3阶振型为绕Z轴扭转。加强层布置对称,结构质心、刚心并未发生本质的变化,且斜腹杆桁架刚度不大,使得振型没有因为加强层发生改变。方案2～方案4的扭转周期比T3/T1分别为0.816、0.825和0.828,与方案1的0.797相比有所增大,说明布置加强层减小了结构扭转刚度,但符合规范0.85限值的要求[4]。从表1可以看出,加强层对低阶自振周期的影响较为明显,使得低阶周期明显变短,对高阶周期影响较小。从加强层数量来看,与方案1相比,方案2、方案3、方案4的第1阶周期分别减小了4.86%、8.63%和9.99%,可见加强层数量越多,结构自振周期下降幅度越大,计算结果与文献[8]得出的结论相同。其中,以布置2个加强层减小幅度最为明显。

4多遇地震下的弹性分析

4.1位移分析

多遇地震下的抗震设计采用CQC组合方式的振型分解反应谱法,实际工程中还需考虑双向地震和偶然偏心。结构在多遇地震作用下的侧向位移结果见表2所列。与方案1相比,方案2、方案3、方案4的X向顶层最大位移分别减小了6.44%、12.11%、14.34%;Y向分别减小了8.80%、16.04%、18.89%。可见加强层能有效控制结构侧移,且随着加强层数量的增加,顶层最大位移和最大位移角的减小量也在增加,但减小幅度有所减小,效果趋于缓和,以布置1道和2道加强层的效果较为明显,实际工程中可以考虑布置2道加强层。从布置效果来看,加强层对减小Y方向的侧移效果要优于X方向。各种方案对侧移的减小幅度均在5%～20%之间。

结构在多遇地震作用下的层间位移角曲线如图2所示。

表2　结构在多遇地震作用下的侧向位移

注:24F表示X向多遇地震下方案1最大位移角所在楼层,其余含义相同。

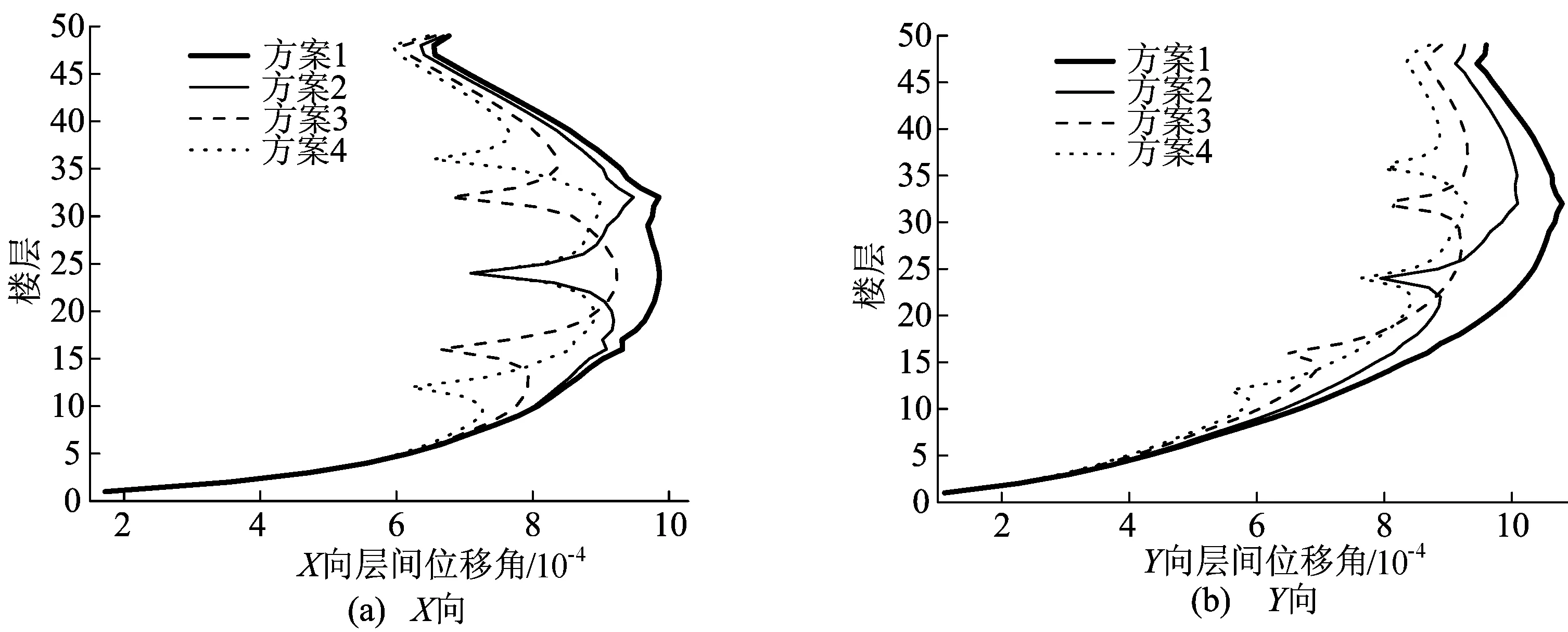
图2　结构在多遇地震作用下的层间位移角

可以看出,加强层能有效地减小结构位移角,随着加强层数量的增加,层间位移角进一步减小。从减小效果来看,每增加1道加强层,层间位移角的减小幅度都在减小,以2道加强层效果最佳。由于加强层的刚度明显大于其他楼层,使得原本均匀的楼层刚度在加强层处急剧变化,这也导致了整个结构的层间位移角曲线呈现分段性和收缩式,加强层将结构分成了若干段,层间位移角在加强层处急剧减小,发生了显著的突变,这势必会造成结构内力的突变,使结构在地震作用下难以呈现“强柱弱梁、强剪弱弯的延性屈服机制,对抗震不利。不过,从加强层造成结构位移角的突变幅度来看,布置1道加强层,层间位移角突变最为明显,布置2道和3道加强层,突变有所缓和。

4.2内力分析

以带2道加强层的方案3为例,方案3结构在X向多遇地震下加强层附近地震剪力的变化幅度见表3所列。

表3　方案3结构在X向多遇地震作用下部分楼层剪力

注:*号表示加强层所在楼层;受剪承载力比为该楼层抗侧力构件的层间受剪承载力与其相邻上一层受剪承载力之比。

从表3中可以看出,楼层剪力分配情况在加强层处发生了突变,在普通楼层(如第34层)外框架承担的剪力不到37%,地震作用下的地震力绝大部分由核心筒承担,但外框架承担的剪力在加强层处大幅增加,且增加的剪力主要由外框架中的钢筋混凝土伸臂和环带支撑承担。与普通楼层(如第33层)相比,在第2道加强层(第32层)处,外框架突变程度达到4.5倍,核心筒达到6.4倍;在第1道加强层(第16层)处,外框架突变达到6.9倍,核心筒达到8.3倍,可见突变较大,但突变范围只局限在加强层及其相邻层,对整体结构剪力变化的影响微小。同时,结构在地震作用下X向和Y向的受剪承载力比最小值分别为0.821(第32层)、0.839(第32层),大于规范限值0.75的要求[4],可见布置加强层后结构并不存在明显的薄弱层。

方案3结构在多遇地震下楼层剪力及弯矩在核心筒和外框架间的分配情况如图3所示。从图3可以看出,加强层的设置会引起核心筒和外框架的弯矩值发生突变,突变范围为加强层所在楼层附近处。

整个结构沿楼层从上到下,每经过1道加强层,核心筒承担的弯矩都会有较大幅度的减小,外框架承担的弯矩都有所增加,但是整体楼层弯矩变化均匀,可见加强层将核心筒承受的倾覆弯矩转移到了外框架上,增加了外框架在地震作用下的贡献,从而提高了结构抗倾覆的能力。

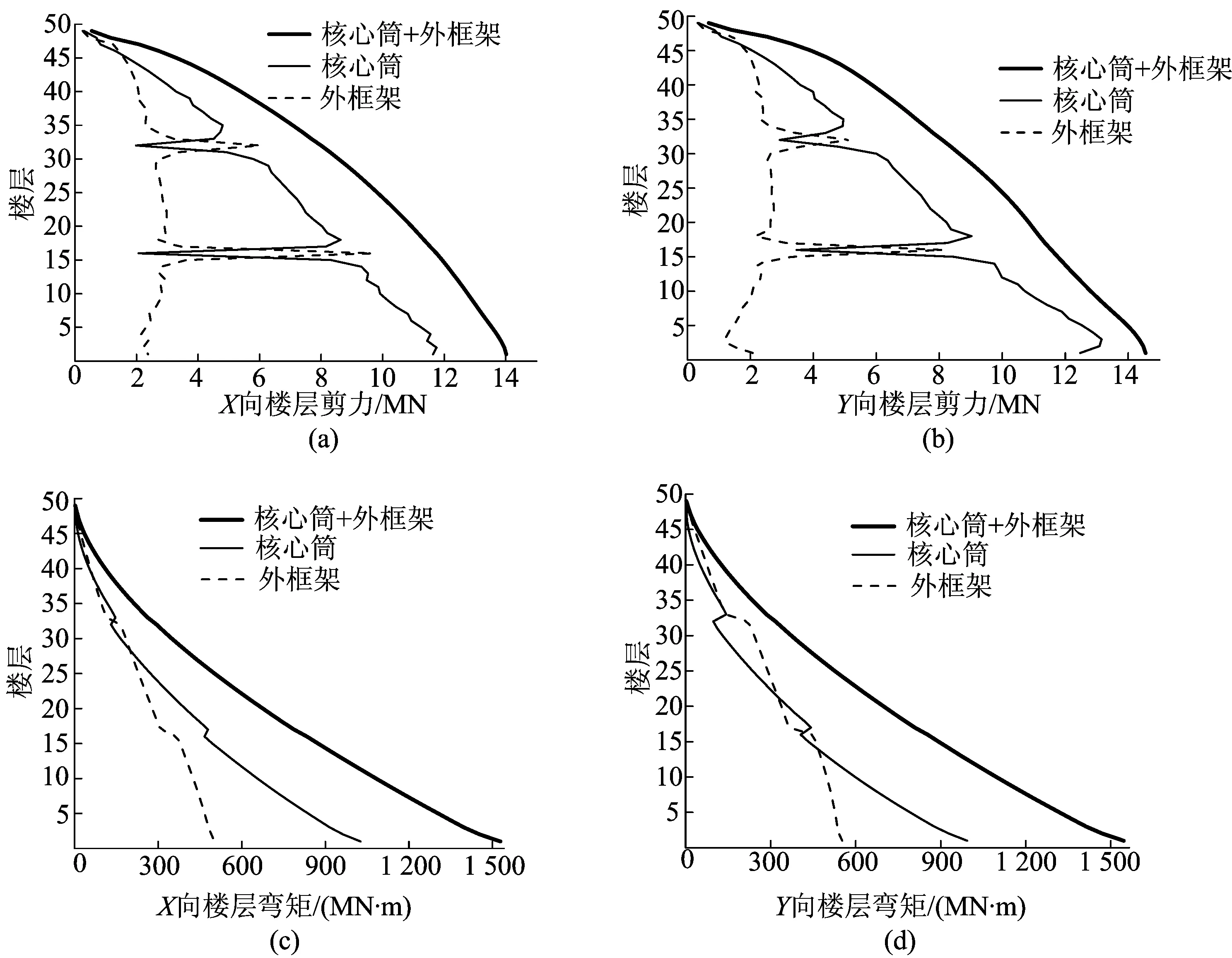
图3　方案3结构在多遇地震作用下的楼层剪力和弯矩分配曲线

5罕遇地震动力弹塑性时程分析

5.1分析模型及计算方法

动力弹塑性分析是将结构作为弹塑性振动体系进行求解,直接按照地震波数据输入地面运动时的加速度,然后求得结构内力和变形随时间变化的全过程。

以下分析中,混凝土本构关系采用了单轴受压应力-应变本构模型[9]。钢筋假定为理想弹塑性材料,本构关系采用简化的二折线模型。钢筋混凝土梁/柱铰采用可以考虑刚度和强度退化的修正武田三折线模型,非线性单元类型为弯矩-旋转角单元。梁铰内力之间为互不相关类型,连梁铰考虑了剪切向非线性特性。柱铰内力之间为变轴力的P-M-M相关类型,剪切铰为互不相关类型。加强层构件采用仅考虑轴力的支撑来模拟。墙单元的剪切特性材料本构关系使用剪力退化三折线模型。剪力墙采用纤维模型来模拟,在考虑剪力墙的轴向弯曲特性的同时,将剪力墙截面定义为包含混凝土纤维和钢筋纤维的截面,其中钢筋纤维的面积用混凝土纤维的配筋率表示。

非线性方程计算采用Newmark-β直接积分法,采用完全牛顿-拉普森法(Newton-Raphson)进行迭代收敛计算直至满足收敛条件,迭代参数中设定的最小时间步长为1×10-5s,最大迭代次数为30次。根据场地条件输入3组地震波(天然波A、天然波B、人工波C),特征周期为0.40 s,有效峰值加速度取220 cm/s2,主次方向按1∶0.85双向输入。采用重力荷载代表值(1DL+0.5LL)为初始状态以获得更接近于实际情况的初始内力,并考虑重力二阶效应。结构阻尼采用瑞利阻尼法,其中质量和刚度因子由选择的2个主振型和对应的阻尼比自动计算,计算过程中自动更新阻尼比。

5.2分析结果

5.2.1结构整体反应指标及抗震性能评价

位移计算结果取3组地震波计算出的平均值进行分析。方案1和方案3在罕遇地震下的顶层相对位移时程曲线和最大弹塑性层间位移角曲线如图4、图5所示。

方案1模型在地震作用下X向和Y向的最大层间位移角分别为1/150(32F)、1/185(26F),最大顶层相对位移分别为833.35、-797.44 mm;方案3模型X向和Y向的最大层间位移角分别为1/157(24F)、1/211(24F),最大顶层相对位移分别为-847.19、-821.11 mm。可以看出,布置加强层后罕遇地震下的最大顶层相对位移略有增大,但依然能有效控制结构层间位移角。与方案1相比,方案3的最大弹塑性层间位移角分别减小了4.46%和12.32%,加强层对Y向的作用效果明显优于X向,与多遇地震相比效果有所下降。

图4　结构顶层相对位移时程曲线

图5　结构最大弹塑性层间位移角

5.2.2结构构件性能评价

由于各地震反应分布规律相似,在天然波B双向作用下结构基底剪力较大,各构件塑性状态比例较多,弹塑性状态变化过程更具代表性,故下面仅以天然波B作用下的结构塑性铰分布状态进行描述和分析。

作为主要耗能构件的连梁(见图1b),大部分梁端进入了第2屈服状态(屈服及屈服后),未发生剪切屈服;框架梁部分进入了第2屈服状态。地震作用下,顶部一些楼层框架梁和连梁梁端率先屈服,再向底部和中间楼层发展,连梁普遍先于框架梁进入屈服状态,形成多道耗能体系。以延性系数D/D2(D为实际发生的总变形值,D2为第2屈服变形值)来判断其损伤程度,该系数越大,则表明塑性发展越多,耗能能力越强,但结构损伤也越大。方案3结构框架梁和连梁在天然波B作用下的延性系数分布如图6所示。

从图6可以看出：仅30%以上框架梁梁端延性系数大于1.0,框架梁损伤较小；约20%连梁梁端延性系数小于1.5,约40%梁端延性系数在1.5～3.0之间,延性系数大于4.0的约占25%,损伤较为严重。由于框架梁和连梁是耗能构件,且分散于不同楼层,尽管塑性损伤较为严重,但不会影响整体安全性。

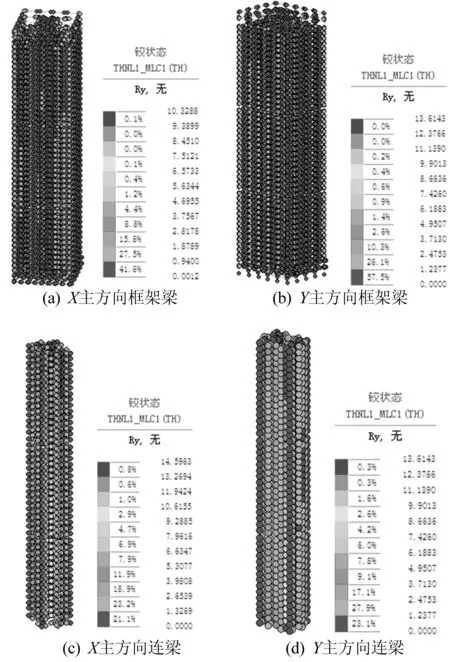
图6　方案3结构框架梁和连梁弯曲延性系数分布图

计算发现,作为主要抗侧力构件的框架柱大部分处于第1屈服状态(开裂及屈服前),虽然柱子较早地出现了第1屈服状态的铰,但整个过程中塑性铰并未继续发展。方案3结构框架柱在天然波B作用下的弯曲延性系数分布如图7所示。

图7　方案3结构框架柱弯曲延性系数分布图

从图7可以看出,框架柱延性系数值均较小,具有良好的二道防线作用。整个过程中梁的延性系数均比柱大,塑性铰发展程度大于柱,因此认为能满足“强柱弱梁”的要求。

地震结束时,部分框架梁、连梁和加强层受力较大的杆件均进入屈服状态,如图8所示。

图8　加强层(16F)框架(梁、柱)受弯弹塑性状态

布置加强层对剪力墙混凝土在水平向和竖向的塑性损伤影响不大,绝大部分处于弹性工作状态,但在底部加强区和加强层边角部位剪切向个别墙肢的局部纤维进入屈服状态,方案1不带加强层屈服比例不足5%,方案3为6%,主要是在加强层部位的墙体屈服比例有所增加,如图9所示。

图9　剪力墙混凝土应变等级弹塑性状态

布置加强层后,加强层处剪力墙混凝土可适当增设钢板,上下楼板厚度由100 mm提高为150 mm,采用双层双向配筋,以保证水平力传递更加有效。加强层刚度不宜过大,刚度过高会增加结构内力的突变程度,易形成薄弱层,宜采用“有限刚度”加强层。

6结论

本文针对某超限高层结构,建立三维模型并布置加强层,对比地震作用下的弹性和弹塑性分析,得出以下结论:

(1) 高层结构布置加强层后,结构自由振动周期和扭转周期比有所下降。加强层数量越多,周期降低越明显,主要集中在低阶振型周期,对高阶周期影响较小。

(2) 布置加强层可以有效控制多遇地震作用结构侧移,包括层间位移角和顶层最大位移,且对Y向作用效果优于X向。加强层对整体结构楼层受力影响不大,但会引起地震剪力和倾覆弯矩在外框架和核心筒间的重分布,造成突变。加强层数量越多,突变越趋缓和。与多遇地震相比,罕遇地震下的加强层作用效果略有降低。

(3) 对于本文混凝土框架-核心筒超限高层结构,可以充分利用避难层布置2道加强层增强结构抗侧力效果,并提高相应的抗震构造措施。

[参考文献]

[1]徐培福，王翠坤，肖从真.中国高层建筑结构发展与展望[J].建筑结构，2009，39(9): 28-32.

[2]沈蒲生.带加强层与错层高层结构设计与施工[M].北京:机械工业出版社,2009:1-6.

[3]徐培福，黄吉峰，肖从真，等.带加强层的框架-核心筒结构抗震设计中的几个问题[J].建筑结构学报,1999,20(4):2-10.

[4]JGJ 3-2010，高层建筑混凝土结构技术规程[S].

[5]杨瑞欣，白良，杨晓东，等.带水平加强层的框架-核心筒结构有限刚度分析[J].工程抗震与加固改造,2012,34(3):22-25,43.

[6]戴雅萍，张敏，王开华，等.张家港双子楼酒店式公寓塔楼结构设计研究[J].建筑结构,2013,43(20):76-83,45.

[7]北京迈达斯技术有限公司.MIDAS Building结构大师用户手册[Z].北京:北京迈达斯技术有限公司，2010.

[8]程红，钱德玲，江曼，等.带加强层的某框架-核心筒结构地震响应分析[J].合肥工业大学学报:自然科学版,2015,38(1):91-94.

[9]GB 50010-2010，混凝土结构设计规范[S].

(责任编辑张淑艳)

Optimization analysis of an out-of-code high-rise building with strengthened storeys

ZHOU Wei,CHENG Chang-zheng

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:An out-of-code high-rise building of 164.0 m height with concrete frame-core tube structure and 49 overground floors is analyzed for the structural optimization. Four finite element models with different strengthened storeys are established using the analysis program Midas Building to analyze the effect of lateral resisting optimization because the depth-width ratio of the core tube in Y direction is a little large. The free vibration analysis, response spectrum analysis under frequent earthquake and dynamic elastoplastic time-history analysis under rare earthquake are conducted in the comparative study. The results can provide a reference for the design of the similar kinds of projects.

Key words:frame-core tube; out-of-code high-rise building; strengthened storey; response spectrum method; dynamic elastoplastic property

收稿日期：2015-08-04；修回日期：2015-09-02

基金项目：国家自然科学基金资助项目(11372094)

作者简介：周伟(1989-),男,安徽合肥人,合肥工业大学硕士生; 程长征(1979-),男,安徽太湖人,博士,合肥工业大学教授,博士生导师.

doi:10.3969/j.issn.1003-5060.2016.05.017

中图分类号:TU973.17

文献标识码：A

文章编号：1003-5060(2016)05-0659-07