并联6-RUS卫星相机像移补偿机构建模与分析

赵延治　赵　飞　杨建涛　李兴兴　赵铁石

1.燕山大学河北省并联机器人与机电系统重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

并联6-RUS卫星相机像移补偿机构建模与分析

赵延治1,2赵飞1,2杨建涛1,2李兴兴1,2赵铁石1,2

1.燕山大学河北省并联机器人与机电系统重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

摘要：将并联6-RUS机构作为卫星相机像移补偿机构，以补偿在轨卫星多维耦合运动引起的像移。基于影响系数理论，利用旋量速度、旋量加速度建立了卫星相机像移补偿机构的运动学模型。利用基于旋量理论的牛顿-欧拉方程，在非惯性系建立了该机构的动力学模型，并分析了非惯性系运动对机构输入的全域影响。该种基于旋量的机构建模方法，利用坐标不变性直接在非惯性系建模，简化了机构建模过程。

关键词：非惯性系；像移补偿；并联机构；旋量理论

0引言

随着卫星遥感应用技术的不断发展，人们对航天遥感设备的分辨力提出了越来越高的要求[1]。目前，高分辨力空间相机大多将推扫成像的线阵TDI CCD(time delayed and integration charge-coupled device)作为焦平面探测器件，其正常工作的基本前提是光生电荷包的转移与焦面上图像的运动保持同步，任何匹配误差都将导致图像模糊[2]。空间相机受到10 μrad的干扰将会导致地面上测量距离误差达500 km[3]。卫星相机在正常推扫时，不可避免地产生正常相移和非正常相移，使图像质量下降甚至恶化[4]。

为了消除像移对卫星相机成像质量的影响，国内外学者提出了机械式补偿、光学式补偿、电子式补偿、图像式补偿等像移补偿方法[5]。目前常用的机械式补偿机构多为二轴、三轴串联转台[6-7]，无法实现对卫星相机姿态的多维耦合补偿。近年来，基于并联机构的多维耦合调姿平台在空间精确指向、稳定跟踪等领域的应用受到越来越多的关注[8]。卫星相机像移补偿平台是处于非惯性系下的多维耦合补偿系统。并联机构在惯性系下的建模方法相对比较成熟[9-11]，在非惯性系下的建模研究工作则相对较少。文献[12]研究了非惯性系动力学的拉格朗日方程，文献[13]建立了转子在非惯性系下的动力学模型，文献[8]利用虚功原理建立了并联舰载稳定平台在非惯性系下的动力学模型。

本文将并联6-RUS折叠式机构作为在轨卫星相机像移补偿机构，将旋量作为运算单元，给出了6-RUS多刚体系统非惯性系的运动学模型；基于牛顿-欧拉方程具有的坐标不变性，建立机构非惯性系动力学模型。

1像移补偿机构构型与符号体系

1.1构型分析

在轨卫星非正常运动包括俯仰、偏航、横滚、横移、纵移。为了补偿以上运动，可在在轨卫星上搭载像移补偿机构以隔离这些扰动，如图1所示。

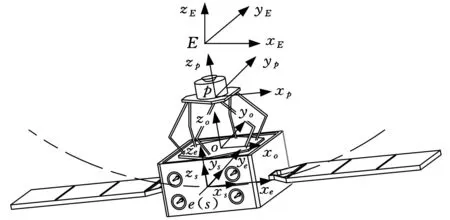
图1　卫星相机像移补偿示意图

如图2所示，本文涉及的并联6-RUS折叠式六自由度机构由下平台、上平台和6个相同的RUS分支组成，各个铰链点布置如图3所示。为减小分支的惯量，将机构中的R副作为驱动副。该机构可以对卫星相机像移进行多维耦合补偿，同时，沿z轴方向的移动自由度还能使机构从工作位置运动到折叠位置，最大限度地减小占用的空间。

图2　6-RUS补偿机构示意图

图3　6-RUS补偿机构铰链点示意图

1.2符号说明

为了实现对在轨卫星位姿的多维耦合补偿，将像移补偿机构的下平台安装在卫星上，将卫星相机安装在补偿机构的上平台，建立图1所示的坐标系，其各坐标系的定义如下：

(1)地心惯性坐标系{E}的原点位于地心，xE轴指向黄经0°，yE轴在赤道平面内，zE轴指向北极。

(2)轨道坐标系{e}的原点位于轨道的任意点，ze轴指向地心，ye轴垂直于轨道平面，xe轴在轨道平面内指向卫星飞行方向并垂直于ze轴。

(3)星体坐标系{s}的原点位于卫星质心处，其3个坐标轴与星体主惯量轴一致，t=0时刻无扰动情况下与轨道坐标系重合。

(4)补偿机构下平台坐标系{o}的原点位于下平台铰链点连接成的六边形中心。初始位置时，其各坐标轴分别与星体坐标系的对应轴平行。

(5)补偿机构上平台坐标系{p}的原点位于上平台铰链点连接成的六边形中心。初始位置时，各坐标轴分别与下平台坐标系的对应轴平行。

上述坐标系中，星体坐标系{s}和补偿机构下平台坐标系{o}为非惯性系，因此卫星相机像移补偿机构是处于非惯性系中的多刚体系统。像移补偿机构下平台相对于地心惯性坐标系{E}的位姿参数可通过卫星上搭载的惯性导航设备获得，而补偿机构上平台及各分支杆件的运动分析均是相对于下平台而言的，故需在非惯性系下分析其运动学、动力学特征。

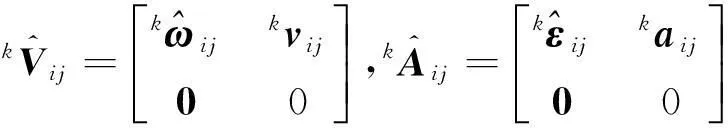
2像移补偿机构非惯性运动学模型

2.1位置反解

令上平台在非惯性系{o}的位姿为

(1)

则上平台坐标系{p}相对于轨道坐标系{e}的变换矩阵为

gep=gesgsogop

(2)

obn=Roppbn+opop

(3)

式中，pbn为铰链点bn在{p}系中的坐标。

令机构的广义输入位移q=(q1，q2，…，q6)，分支中间铰链点cn在{o}系中的坐标可由约束方程获得：

(4)

其中，lcbn、lcan分别为连杆cnbn、连杆cnan的长度；oSn为分支转动副轴线矢量在{o}系中的表示。因此，像移补偿机构的广义输入位移方程为

(5)

式中，olcan为从铰链点an指向铰链点cn的矢量在{o}系中的表示；zo为{o}系z轴的单位向量。

2.2速度分析

上平台坐标系{p}与卫星坐标系{s}相对于惯性系{e}的旋量速度可以通过惯性导航系统的测量求得。由文献[14]可知

(6)

则上平台相对于{o}系的旋量速度在{o}系中的表示为

(7)

则上平台对第r个分支运动副变量的一阶影响系数矩阵为

(8)

图4　6-RUS补偿机构分支示意图

进而可得上平台在{o}系下的旋量速度与驱动速度的映射关系：

(9)

其中，qGp为非惯性系下，上平台旋量速度与广义速度的映射矩阵。驱动速度与第r分支的第k个杆件在{o}系下的旋量速度的映射关系为

(10)

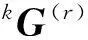
2.3加速度分析

旋量加速度是李代数se(3)的元素，由多刚体系统旋量加速度伴随变换[15]可得，{p}系相对于{o}系的旋量加速度在{o}系中的表示为

(11)

其中，[eVes,eVop]=eVeseVop-eVopeVes，表示旋量eVes和eVop作李括弧运算。eAes、eAep均可由惯性导航系统测得。由影响系数理论[16]可知：

(12)

pGq=[qGp]-1

其中，pHq为驱动输入映射到动平台的二阶影响系数矩阵。则驱动副的输入加速度为

(13)

同理可得第r分支6个运动关节的加速度:

(14)

根据式(12)可得第r分支第k个杆件相对于{o}系的旋量加速度在{o}系中的表示：

(15)

3像移补偿机构非惯性系动力学模型

3.1基于旋量加速度的牛顿-欧拉公式

令坐标系{j}固连在刚体J上，原点在刚体J的质心；令坐标系{i}为参考坐标系。由基于旋量理论的牛顿-欧拉公式[17-18]可知，刚体J的惯性力螺旋在{j}系中的表示为

(16)

其中，jN为刚体J的6维惯性张量矩阵；m为刚体J的质量；jI为刚体J的转动惯量在{j}系中的表示；I3为3×3的单位阵。刚体J的惯性力螺旋在{i}系中的表示为

(17)

其中，iN为刚体J的惯性张量在{i}系中的表示。由式(16)、式(17)可知，基于旋量理论的牛顿-欧拉方程在不同坐标系下的表达式具有相同的形式，即具有坐标不变性。基于这一特性，可直接将动力学方程表示在非惯性系下，从而避免繁琐的变换，简化补偿机构在非惯性系的动力学建模过程。

3.2非惯性系下像移补偿机构动力学模型

非惯性系{o}中，补偿机构上平台相对于惯性系的惯性力旋量为

(18)

其中，oNp为上平台相对于非惯性系{o}的惯性张量。将式(7)、式(11)代入式(18)并整理可得

(19)

式(19)中，等号右边第一项只与机构主动运动有关，称之为主动运动惯性力旋量；第二项只与非惯性系运动有关，称之为牵连惯性力旋量；第三项为由卫星运动和机构主动运动耦合引起的惯性力旋量，称之为科氏惯性力旋量。

由于机构的一阶影响系数矩阵只与机构的形位有关，与坐标系的运动无关，故在非惯性系{o}中，将上平台相对于惯性系的惯性力旋量映射到驱动关节，即

(20)

同理，非惯性系下像移补偿机构各分支杆件的惯性力旋量引起的广义驱动力也可按上述方法得到。

忽略关节摩擦力和重力，根据达朗伯原理，建立非惯性系下像移补偿机构的动力学模型：

(21)

4数值算例

4.1仿真模型参数

某并联6-RUS像移补偿机构，设其上平台铰链点外接圆直径db=3.5 m，夹角αb=100°；下平台铰链点外接圆直径da=5.0 m，夹角αa=64.85°。上平台的质量mP=36.65 kg，分支上下连杆的长度lcb=2.5 m，lac=1.5 m，质量mcb=0.91 kg，mac=0.64 kg，上平台、上杆、下杆相对于各自质心的转动惯量分别为

pIp=diag(56.40,28.37,28.37)kg·m2

iIcb=diag(0.57,0.57,6.45×10-3)kg·m2

iIac=diag(0.21,0.21,8.87×10-3)kg·m2

坐标系{p}相对于坐标系{o}的初始位置为(0, 0, 3 m)，方位重合。坐标系{o}相对于坐标系{s}的初始位置为(0, 0, 1)m。假定卫星受外界环境的干扰产生绕其质心的俯仰和滚转的耦合运动(其运动规律按xyz欧拉角描述)。绕x轴转动角度θx=10°sint；绕y轴转动角度θy=10°sint；绕z轴转动角度θz=0。

4.2模型验证

通过上文所建立的非惯性系像移补偿机构的动力学模型，可以求得补偿机构在补偿卫星扰动时，各驱动关节的加速度和驱动力矩，如图5、图6所示。

图5　像移补偿机构驱动加速度计算结果

图6　像移补偿机构驱动力矩计算结果

为验证所建模型的正确性，在ADAMS中建立该机构的虚拟样机，并建立地心惯性坐标系、轨道坐标系、星体坐标系、补偿机构下平台坐标系、补偿机构上平台坐标系。以上述数值算例参数为例进行仿真分析，结果如图7、图8所示。

图7　像移补偿机构驱动加速度仿真结果

图8　像移补偿机构驱动力矩仿真结果

对比图5、图7所示的驱动加速度曲线，以及图6、图8所示的驱动力矩曲线可知，模型理论计算结果与仿真数据基本一致。图9所示为像移补偿机构驱动力矩计算结果和仿真结果的误差曲线， 6个分支的误差绝对值均小于0.04N·m，从而验证了所建模型的正确性。

图9　驱动力矩计算结果和仿真结果误差曲线

4.3驱动输入分析

图10　主动运动引起的驱动力矩

图11　牵连运动引起的驱动力矩

图12　科氏运动引起驱动力矩

结合式(19)、式(21)，分别计算像移补偿机构主动运动、牵连运动、科氏运动引起的驱动力矩，如图10～图12所示。对比图10、图11可知，在给定的运动规律下，主动运动引起的驱动力矩和牵连运动引起的驱动力矩在任一时刻方向相反，数值相近，这表明为了保证补偿机构上平台相对惯性系的位姿稳定，主动运动引起的驱动力矩绝大部分用以抵消由卫星的运动引起的牵连惯性力。由图12可知，科氏运动引起的驱动力矩数值相对较小且方向保持不变。主动运动引起的驱动力矩、牵连运动引起的驱动力矩和科氏运动引起的驱动力矩相互叠加，共同决定了补偿机构上平台保持稳定各驱动关节所需的驱动力矩。补偿机构上平台运动规律改变或卫星扰动规律变化都会造成主动运动、牵连运动和科氏运动的变化。

4.4非惯性系运动对机构输入全域的影响

上述算例是在给定卫星运动和补偿机构上平台运动规律时得到的，本节将考察非惯性全域运动空间，分析非惯性系运动对机构输入的影响。

分别令上平台相对于惯性系的xyz欧拉角ε为(0°，0°，0°)和(-5°，3°，0°)。假定卫星受外界环境的干扰产生绕其质心的俯仰和滚转的耦合运动，其运动规律为θx=10°sint，θy=10°sint，θz=0。仅考虑卫星运动引起的牵连运动和科氏运动对广义输入的影响，为表征非惯性运动对广义输入的影响，定义非惯性系下广义输入极值τm=max(|τq+τk|)，其中τq+τk为由牵连运动与科氏运动共同引起的广义输入的最大值。补偿机构处于给定的不同位姿下，非惯性系全域空间内该极值的变化曲面分别如图13、图14所示。

图13　ε = (0°，0°，0°) 时非惯性牵连运动与科氏运动全域输入曲面

图14　ε = (-5°，3°，0°) 时非惯性牵连运动与科氏运动全域输入曲面

分析对比图13、图14可知，当补偿机构位姿确定时，非惯性系下的广义输入极值随非惯性系运动而变化；当非惯性系的运动规律确定时，补偿机构不同位姿下广义输入极值的分布规律也明显不同。图13中，俯仰转角为10°、横滚转角为-10°时，广义输入极值最大为30.9713N·m；俯仰转角为0°、横滚转角为0°时，广义输入极值最小为4.3272N·m。图14中，俯仰转角为10°、横滚转角为-10°时，广义输入极值最大为29.6261N·m；俯仰转角为0°、横滚转角为0°时，广义输入极值最小为4.0191N·m。当非惯性系运动规律不变时，不同位姿下广义输入极值的最大、最小值所在位置虽然相同，但最大、最小值的数值大小随补偿机构初始位姿的不同而不同。综上所述，非惯性系对补偿机构广义输入的影响由非惯性系的运动和补偿机构的位姿共同决定。

5结论

(1)针对卫星相机的像移补偿需求，将并联6-RUS折叠式六自由度机构用于补偿在轨卫星多维耦合运动引起的像移。利用旋量速度、旋量加速度在不同坐标系下的伴随变换，建立了非惯性系下补偿机构的运动学模型。

(2)利用基于旋量理论的牛顿-欧拉公式所具有的坐标不变性，直接将动力学方程表示在非惯性系下，并结合影响系数理论，有效简化了非惯性系下补偿机构的动力学求解过程。建模始终以旋量为基本运算单元，使得建模过程简洁，易于编程。

(3)通过仿真对建模方法的正确性进行了验证，并分析了动力学模型各组成部分所引起的驱动力矩以及非惯性系运动对机构输入的全域影响。

参考文献：

[1]杨秉新. 国外航天侦察相机和测绘相机发展概况[J]. 航天返回与遥感, 1998, 19 (2) : 16-24.

YangBingxin.TheDevelopmentSurveyofForeignSpaceReconnaissanceCameraandMappingCamera[J].SpacecraftRecovery&RemoteSensing, 1998, 19(2): 16-24.

[2]HuangQianlin,LiXiangmin.ApplicationofTDICCDonReal-timeEarthReconnaissanceSatellite[C]//Proc.ofSPIE,AutomatedOpticalInspectionforIndustry:TheoryTechnologyandApplicationsⅡ.Beijing，1998：93-104.

[3]AndersonEH,FumoJP,ErwinRS，etal.SatelliteUltraquietIsolationTechnologyExperiment(SUITE):ElectromechanicalSubsystems[C]//SPIESmartStructuresandMaterials1999:IndustrialandCommercialApplicationsofSmartStructuresTechnologies.NewportBeach，CA，USA，2002: 299-313.

[4]陈世平. 关于遥感图像品质的若干问题[J]. 航天返回与遥感,2009,30(2):10-16.

ChenShiping.SomeIssuesabouttheRemoteSensingImageQuality[J].SpacecraftRecovery&RemoteSensing, 2009,30(2):10-16.

[5]刘明,匡海鹏,吴宏圣,等. 像移补偿技术综述[J]. 电光与控制,2004,11(4): 46-49.

LiuMing,KuangHaipeng,WuHongsheng,etal.SurveyontheImageMotionCompensationTechnology[J].ElectronicsOptics&Control, 2004，11(4): 46-49.

[6]刘剑峰, 韩琦琦, 于思源,等. 卫星光通信终端二维转台运动参量对天线指向影响研究[J]. 宇航学报,2007,28(4): 926-931.

LiuJianfeng,HanQiqi,YuSiyuan,etal.ResearchontheInfluenceoftheMotionParametersoftheSatelliteOpticalCommunicationTerminal’sGimbalsonAntennaPointingError[J].JournalofAstronautics, 2007，28(4)：926-931.

[7]谷松,王绍举. 空间相机调偏流机构的设计与控制[J]. 光学精密工程, 2009,17(3): 615-620.

GuSong,WangShaoju.DesignandControlofDriftAdjustingMechanisminSpaceCamera[J].OpticsandPrecisionEngineering, 2009,17(3): 615-620.

[8]刘晓, 赵铁石, 李二伟, 等. 非惯性系折叠式并联稳定平台机构建模及分析[J]. 机械工程学报, 2013, 49(17): 101-109.

LiuXiao,ZhaoTieshi,LiErwei,etal.ModelingandAnalysisofFoldableParallelStabilizedPlatforminNon-inertialSystem[J].JournalofMechanicalEngineering, 2013, 49(17): 101-109.

[9]HeJ,GaoF,BaiY,etal.DynamicModelingandExperimentofaNewTypeofParallelServoPressConsideringGravityCounterbalance[J].ChineseJournalofMechanicalEngineering, 2013, 26(6): 1222-1233.

[10]YangC,HanJ,ZhengS,etal.DynamicModelingandComputationalEfficiencyAnalysisforaSpatial6-DOFParallelMotionSystem[J].NonlinearDynamics, 2012, 67(2): 1007-1022.

[11]LiuS,YuY,ZhuZ,etal.DynamicModelingandAnalysisof3-RRSParallelManipulatorwithFlexibleLinks[J].JournalofCentralSouthUniversityofTechnology, 2010, 17: 323-331.

[12]范宝同. 用拉格朗日方法处理非惯性系动力学问题探讨[J]. 太原教育学院学报, 2001, 19(1): 39-42.

FanBaotong.ExploringtheDynamicProbleminNon-inertialSystembyLagrangianEquation[J].JournalofTaiyuanInstituteofEducation, 2001,19(1):39-42.

[13]林富生, 黄其柏, 孟光. 单自由度非惯性系内转子系统的动力学特性研究[J]. 武汉理工大学学报(交通科学与工程版), 2007, 31(4): 627-629.

LinFusheng,HuangQibo,MengGuang.DynamicCharacteristicsofanUnbalancedRotorSysteminaNon-inertialSystemwithOneDegreeofFreedom[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering)，2007，31(4)：627-629.

[14]理查德·摩雷, 李泽湘, 夏恩卡·萨思特里. 机器人操作的数学导论[M]. 徐卫良，钱瑞明，译.北京: 机械工业出版社, 1995.

[15]ZhaoTS,LiuX,YuanFH,etal.AccelerationAnalysisofRigidBodyandItsApplicationforShip-basedStabilizedPlatformSystem[EB/OL].Beijing:SciencepaperOnline, 2013-02-25[2014-05-20].http://www.paper.edu.cn/releasepaper/content/201302-420.html.

[16]黄真，赵永生，赵铁石.高等空间机构学[M].北京：高等教育出版社，2006.

[17]ZhaoTS,GengMC,ChenYH,etal.KinematicsandDynamicsHessianMatricesofManipulatorsBasedonScrewTheory[J].ChineseJournalofMechanicalEngineering, 2015, 28(2): 226-235.

[18]耿明超, 赵铁石, 赵飞, 等. 6-UPRRUS折叠式并联机构及其动力学模型[J].中国机械工程, 2015, 26(4): 456-462.

GengMingchao,ZhaoTieshi,ZhaoFei,etal.A6-UPRRUSFoldableParallelMechanismandItsDynamicsModel[J].ChinaMechanicalEngineering, 2015, 26(4): 456-462.

(编辑张洋)

Modelling and Analysis of 6-RUS Parallel Mechanism of Image Compensation of Satellite Camera

Zhao Yanzhi1,2Zhao Fei1,2Yang Jiantao1,2Li Xingxing1,2Zhao Tieshi1,2

1.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System，Qinhuangdao，Hebei，066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science，Qinhuangdao，Hebei，066004

Abstract:A parallel 6-RUS mechanism was used as the compensation platform for image motion which was caused by the multi-dimensional motion of the satellite. Based on influence coefficient theory, the kinematics model of this mechanism was built by velocity screw and acceleration screw. The dynamics model of this parallel platform in non-inertial frame was developed taking advantage of Newton-Euler’s equation based on screw theory, and then the influence of the motion of the non-inertial frame on input of the mechanism in the whole working space was analysed. This mechanism modeling method was simplified with screw using coordinate-invariant in the non-inertial system.

Key words:non-inertial system; compensation for image motion; parallel mechanism; screw theory

收稿日期：2015-03-17

基金项目：国家自然科学基金资助项目(51105322)；河北省自然科学基金资助项目(E2014203176)；河北省高等学校自然科学研究基金资助项目(QN2015040)

中图分类号：TP24; TH112

DOI：10.3969/j.issn.1004-132X.2016.03.016

作者简介：赵延治，男，1981年生。燕山大学机械工程学院副教授。主要研究方向为并联机器人机构学理论与应用。发表论文20余篇。赵飞，男，1988年生。燕山大学机械工程学院硕士研究生。杨建涛，男，1988年生。燕山大学机械工程学院硕士研究生。李兴兴，女，1989年生。燕山大学机械工程学院硕士研究生。赵铁石，男，1963年生。燕山大学机械工程学院教授、博士研究生导师。